10.4: Conteo
- Page ID
- 113039
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)¿Contando? Ya sabes contar o no estarías tomando una clase de matemáticas de nivel universitario, ¿verdad? Pues sí, pero lo que realmente vamos a estar investigando aquí son formas de contar de manera eficiente. Cuando lleguemos a las situaciones de probabilidad un poco más adelante en este capítulo, tendremos que contar algunos números muy grandes, como el número de posibles boletos ganadores de lotería. Una forma de hacerlo sería anotar cada conjunto posible de números que pudieran aparecer en un boleto de lotería, pero créeme: no quieres hacer esto.
Conteo Básico
Empezaremos, sin embargo, con algunos tipos de problemas de conteo más razonables para desarrollar las ideas que pronto necesitaremos.
Supongamos que en un restaurante en particular tienes tres opciones para un aperitivo (sopa, ensalada o palitos de pan) y cinco opciones para un plato principal (hamburguesa, sándwich, quiche, fajita o pizza). Si se le permite elegir exactamente un artículo de cada categoría para su comida, ¿cuántas opciones de comida diferentes tiene?
Solución
Solución 1: Una forma de resolver este problema sería enumerar sistemáticamente cada comida posible:
| sopa + hamburguesa | sopa + sandwich | sopa + quiche |
| sopa + fajita | sopa + pizza | ensalada + hamburguesa |
| ensalada + sandwich | ensalada + quiche | ensalada + fajita |
| ensalada + pizza | palitos de pan + hamburguesa | palitos de pan + sandwich |
| palitos de pan + quiche | palitos de pan + fajita | palitos de pan + pizza |
Suponiendo que lo hicimos sistemáticamente y que no perdimos ninguna posibilidad ni enumeramos ninguna posibilidad más de una vez, la respuesta sería 15. Así, podrías ir al restaurante 15 noches seguidas y tener una comida diferente cada noche.
Solución 2: Otra forma de resolver este problema sería enumerar todas las posibilidades en una tabla:
| hamburguesa | sandwich | quiche | fajita | pizza | |
| sopa | sopa + hamburguesa | ||||
| ensalada | ensalada + hamburguesa | ||||
| pan | etc. |
En cada una de las celdas de la tabla podríamos enumerar la comida correspondiente: sopa + hamburguesa en la esquina superior izquierda, ensalada + hamburguesa debajo de ella, etc. pero si realmente no nos importaba cuáles son las comidas posibles, solo cuántas comidas posibles hay, solo podríamos contar el número de celdas y llegar a una respuesta de 15, que coincide con nuestra respuesta desde la primera solución. (¡Siempre es bueno cuando resuelves un problema de dos maneras diferentes y obtienes la misma respuesta!)
Solución 3: Ya tenemos dos soluciones perfectamente buenas. ¿Por qué necesitamos un tercio? El primer método no fue muy sistemático, y podríamos haber hecho fácilmente una omisión. El segundo método fue mejor, pero supongamos que además del aperitivo y el plato principal complicamos aún más el problema al agregar postres al menú: hemos usado las filas de la mesa para los aperitivos y las columnas para los platos principales, ¿a dónde irán los postres? Necesitaríamos una tercera dimensión, y como dibujar tablas 3-D en una página 2-D o pantalla de computadora no es terriblemente fácil, necesitamos una mejor manera en caso de que tengamos tres categorías para elegir forma en lugar de solo dos.
Entonces, volvamos al problema en el ejemplo. ¿Qué más podemos hacer? Dibujemos un diagrama de árbol:
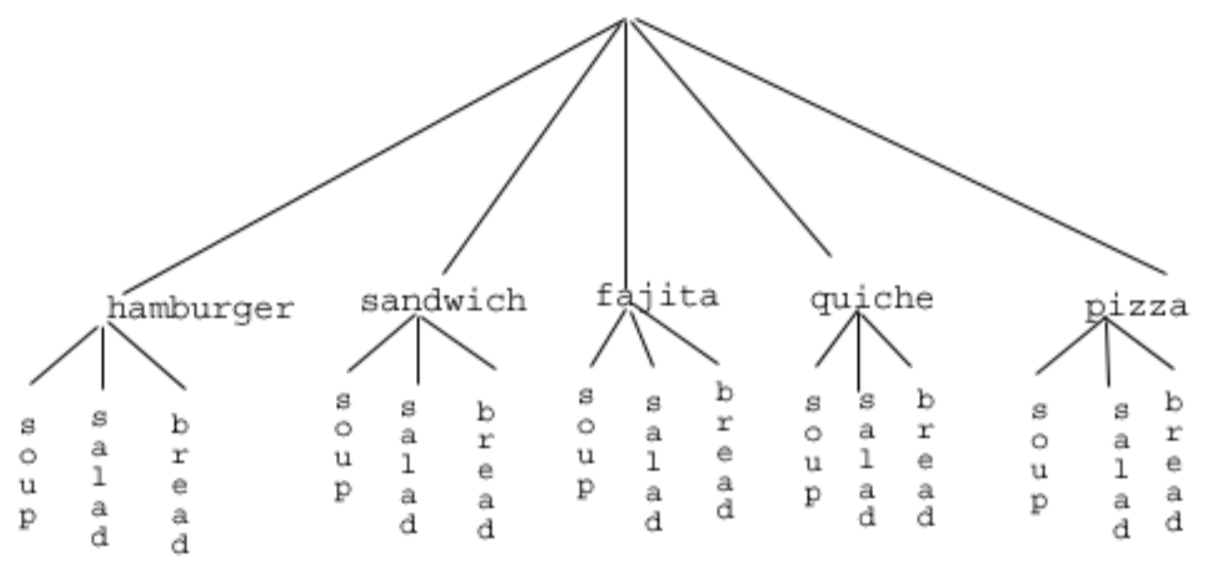
Esto se llama diagrama de “árbol” porque en cada etapa nos ramificamos, como las ramas de un árbol. En este caso, primero dibujamos cinco sucursales (una por cada plato principal) y luego para cada una de esas ramas dibujamos tres ramas más (una por cada aperitivo). Contamos el número de sucursales en el nivel final y obtenemos (¡sorpresa, sorpresa!) 15.
Si quisiéramos, en cambio podríamos dibujar tres ramas en la primera etapa para los tres aperitivos y luego cinco ramas (una por cada plato principal) ramificándose de cada una de esas tres ramas.
Ok, entonces ahora sabemos contar posibilidades usando tablas y diagramas de árbol. Estos métodos seguirán siendo útiles en ciertos casos, pero imagina un juego en el que tengas dos barajas de cartas (con 52 cartas en cada mazo) y selecciones una carta de cada mazo. ¿De verdad querrías dibujar un diagrama de tabla o árbol para determinar el número de resultados de este juego?
Volvamos al ejemplo anterior que implicaba seleccionar una comida de tres aperitivos y cinco platos principales, y veamos la segunda solución que utilizó una mesa. Observe que una forma de contar el número de comidas posibles es simplemente numerar cada una de las celdas apropiadas en la tabla, como hemos hecho anteriormente. Pero otra forma de contar el número de celdas en la tabla sería multiplicar el número de filas (3) por el número de columnas (5) para obtener 15. Observe que podríamos haber llegado al mismo resultado sin hacer una mesa en absoluto simplemente multiplicando el número de opciones para el aperitivo (3) por el número de opciones para el plato principal (5). Generalizamos esta técnica como regla básica de conteo:
Si se nos pide elegir un artículo de cada una de las dos categorías separadas donde hay\(m\) artículos en la primera categoría y\(n\) artículos en la segunda categoría, entonces el número total de opciones disponibles es\(m \cdot n\).
Esto a veces se llama la regla de multiplicación para las probabilidades.
Hay 21 novelas y 18 volúmenes de poesía en una lista de lectura para un curso de inglés universitario. ¿De cuántas maneras diferentes puede un estudiante seleccionar una novela y un volumen de poesía para leer durante el trimestre?
Solución
Hay\(21\) opciones desde la primera categoría y\(18\) para la segunda, por lo que hay\(21 \cdot 18 = 378\) posibilidades.
La Regla de Conteo Básico se puede extender cuando hay más de dos categorías aplicándola repetidamente, como vemos en el siguiente ejemplo.
Supongamos que en un restaurante en particular tienes tres opciones para un aperitivo (sopa, ensalada o palitos de pan), cinco opciones para un plato principal (hamburguesa, sándwich, quiche, fajita o pasta) y dos opciones de postre (pastel o helado). Si se le permite elegir exactamente un artículo de cada categoría para su comida, ¿cuántas opciones de comida diferentes tiene?
Solución
Hay\(3\) opciones para un aperitivo,\(5\) para el plato principal y\(2\) para el postre, así que hay\(3 \cdot 5 \cdot 2 = 30\) posibilidades.
Un cuestionario consta de 3 preguntas verdaderas o falsas. ¿De cuántas maneras puede responder el cuestionario un alumno?
Solución
Hay\(3\) preguntas. Cada pregunta tiene\(2\) posibles respuestas (verdaderas o falsas), por lo que el cuestionario puede ser respondido de\(2 \cdot 2 \cdot 2 = 8\) diferentes maneras. Recordemos que otra forma de escribir\(2 \cdot 2 \cdot 2\) es\(2^3\), que es mucho más compacta.
Supongamos que en un restaurante en particular tienes ocho opciones para un aperitivo, once opciones para un plato principal y cinco opciones de postre. Si se le permite elegir exactamente un artículo de cada categoría para su comida, ¿cuántas opciones de comida diferentes tiene?
Permutaciones
En esta sección, desarrollaremos una forma aún más rápida de resolver algunos de los problemas que ya hemos aprendido a resolver por otros medios. Empecemos con un par de ejemplos.
¿De cuántas maneras diferentes se pueden reordenar las letras de la palabra MATH para formar una palabra clave de cuatro letras?
Solución
Este problema es un poco diferente. En lugar de elegir un elemento de cada una de varias categorías diferentes, estamos eligiendo repetidamente elementos de la misma categoría (la categoría es: las letras de la palabra MATH) y cada vez que elegimos un artículo no lo reemplazamos, por lo que hay una opción menos en la siguiente etapa: tenemos 4 opciones para la primera letra (digamos que elegimos A), luego 3 opciones para la segunda (M, T y H; digamos que elegimos H), luego 2 opciones para la siguiente letra (M y T; digamos que elegimos M) y solo una opción en la última etapa (T). Así, hay\(4 \cdot 3 \cdot 2 \cdot 1 = 24\) formas de deletrear un código que valga la pena con las letras MATH.
En este ejemplo, necesitábamos calcular\(n \cdot (n – 1) \cdot (n – 2) ··· 3 \cdot 2 \cdot 1\). Este cálculo aparece a menudo en matemáticas, y se llama el factorial, y se anota\(n!\)
Un factorial es cuando tomamos un entero positivo y encontramos el producto de todos los enteros positivos descendentes, incluyéndose a sí mismo, todo el camino hasta 1:
\[n! = n \cdot (n – 1) \cdot (n – 2) ··· 3 \cdot 2 \cdot 1 \nonumber \]
Decimos\(n!\) como “\(n\)factorial”. Por ejemplo, dado 5! , entonces decimos “5 factoriales”.
¿De cuántas formas se pueden distribuir cinco premios puerta diferentes entre cinco personas?
Solución
Hay 5 opciones de premio para la primera persona, 4 opciones para la segunda, y así sucesivamente. El número de formas en que se pueden distribuir los premios serán\(5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120\) formas.
Ahora consideraremos algunos ejemplos ligeramente diferentes.
Un beneficio benéfico es atendido por 25 personas y se regalan tres certificados de regalo como premios de puerta: un certificado de regalo es de $100, el segundo vale $25 y el tercero vale $10. Asumiendo que ninguna persona recibe más de un premio, ¿de cuántas formas diferentes se pueden otorgar los tres certificados de regalo?
Solución
Usando la regla básica de conteo, hay 25 opciones para la persona que recibe el certificado de $100, 24 opciones restantes para el certificado de $25 y 23 opciones para el certificado de $10, por lo que hay\(25 \cdot 24 \cdot 23 = 13,800\) formas en que se pueden otorgar los premios.
Ocho velocistas han llegado a la final olímpica en la carrera de 100 metros. ¿De cuántas formas diferentes se pueden otorgar las medallas de oro, plata y bronce?
Solución
Usando la Regla de Conteo Básico, hay 8 opciones para el ganador de la medalla de oro, 7 opciones restantes para la plata y 6 para el bronce, por lo que hay\(8 \cdot 7 \cdot 6 = 336\) formas en que las tres medallas se pueden otorgar a los 8 corredores.
Tenga en cuenta que en estos ejemplos anteriores, los certificados de regalo y las medallas olímpicas se entregaron sin reemplazo; es decir, una vez que hemos elegido a un ganador del premio de primera puerta o de la medalla de oro, no son elegibles para los demás premios. Así, en cada etapa sucesiva de la solución hay una opción menos (25, luego 24, luego 23 en el primer ejemplo; 8, luego 7, luego 6 en el segundo). Contraste esto con la situación de una prueba de opción múltiple, donde podría haber cinco respuestas posibles —A, B, C, D o E— para cada pregunta de la prueba.
Tenga en cuenta también que el orden de selección era importante en cada ejemplo: para los premios de tres puertas, ser elegido primero significa que recibes sustancialmente más dinero; en el ejemplo de Olimpiadas, entrar primero significa que obtienes la medalla de oro en lugar de la plata o el bronce. En cada caso, si hubiéramos elegido a las mismas tres personas en un orden diferente podría haber habido una persona diferente que recibió el premio de $100, o un medallista de oro diferente. (Contraste esto con la situación en la que podríamos sacar tres nombres de un sombrero para que cada uno reciba un certificado de regalo de $10; en este caso, el orden de selección no es importante ya que cada una de las tres personas recibe el mismo premio. Situaciones, donde el orden no es importante, serán discutidas en la siguiente sección.)
Podemos generalizar la situación en los dos ejemplos anteriores a cualquier problema sin reemplazo donde el orden de selección sea importante. Si estamos arreglando en orden r artículos fuera de n posibilidades (en lugar de 3 de 25 o 3 de 8 como en los ejemplos anteriores), el número de arreglos posibles vendrá dado por
\[n \cdot (n – 1) \cdot (n – 2) ··· (n – r + 1) \nonumber \]
Si no ves por qué\((n — r + 1)\) es el número correcto para usar para el último factor, solo piensa en el primer ejemplo de esta sección, donde calculamos\(25 \cdot 24 \cdot 23\) para obtener\(13,800\). En este caso\(n = 25\) y\(r = 3\), así\(n — r + 1 = 25 — 3 + 1 = 23\), cuál es exactamente el número correcto para el factor final.
Ahora bien, ¿por qué querríamos usar esta complicada fórmula cuando en realidad es más fácil usar la Regla de Conteo Básico, como hicimos en los dos primeros ejemplos? Bueno, en realidad no usaremos esta fórmula con tanta frecuencia, solo la desarrollamos para que pudiéramos adjuntar una notación especial y una definición especial a esta situación en la que estamos eligiendo\(r\) artículos fuera de\(n\) posibilidades sin reemplazo y donde el orden de selección es importante.
\[_nP_r = n \cdot (n – 1) \cdot (n – 2) ··· (n – r + 1) \nonumber \]
Decimos que hay permutaciones nPr de tamaño r que pueden seleccionarse de entre n opciones sin reemplazo cuando el orden importa.
Resulta que podemos expresar este resultado de manera más simple usando factoriales.
\[_nP_r = \dfrac{n!}{(n-r)!} \nonumber \]
En la practicidad, solemos utilizar tecnología en lugar de factoriales o multiplicación repetida para calcular permutaciones.
Tengo nueve cuadros y tengo espacio para exhibir solo cuatro de ellos a la vez en mi pared. ¿De cuántas maneras diferentes podría hacer esto?
Solución
Ya que estamos eligiendo\(4\) pinturas fuera de\(9\) sin reemplazo donde el orden de selección es importante hay\(_9P_4 = 9 \cdot 8 \cdot 7 \cdot 6 = 3,024\) permutaciones.
¿De cuántas maneras se puede seleccionar un comité ejecutivo de cuatro personas (presidente, vicepresidente, secretario, tesorero) de una junta directiva de 16 miembros de una organización sin fines de lucro?
Solución
Queremos elegir\(4\) personas fuera de\(16\) sin reemplazo y donde el orden de selección es importante. Entonces, la respuesta es\(_16P_4 = 16 \cdot 15 \cdot 14 \cdot 13 = 43,680\).
Cuántas contraseñas de 5 caracteres se pueden hacer usando las letras de la A a la Z
a. si se permiten repeticiones
b. si no se permiten repeticiones
Combinaciones
En el apartado anterior, consideramos la situación en la que elegimos\(r\) artículos fuera de\(n\) posibilidades sin reemplazo y donde el orden de selección era importante. Consideramos ahora una situación similar en la que el orden de selección no es importante.
Un beneficio benéfico es atendido por 25 personas en las que se regalan tres certificados de regalo de $50 como premios de puerta. Suponiendo que ninguna persona reciba más de un premio, ¿de cuántas formas diferentes se pueden otorgar los certificados de regalo?
Solución
Usando la Regla de Conteo Básico, hay 25 opciones para la primera persona, 24 opciones restantes para la segunda persona y 23 para la tercera, por lo que hay\(25 \cdot 24 \cdot 23 = 13,800\) formas de elegir a tres personas. Supongamos por un momento que Abe es elegido primero, Bea segundo y Cindy tercero; este es uno de los 13 mil 800 posibles resultados. Otra forma de otorgar los premios sería elegir a Abe primero, Cindy segundo y Bea tercero; este es otro de los\(13,800\) posibles resultados. Pero de cualquier manera Abe, Bea y Cindy reciben cada uno $50, así que realmente no importa el orden en que los seleccionemos. ¿En cuántos pedidos diferentes se pueden seleccionar Abe, Bea y Cindy? Resulta que hay 6:
ABC ACB BAC BCA CABINA CBA
¿Cómo podemos estar seguros de que los hemos contado todos? Realmente solo estamos eligiendo a\(3\) las personas\(3\), así que hay\(3 \cdot 2 \cdot 1 = 6\) formas de hacerlo; realmente no necesitábamos enumerarlas todas, ¡solo podemos usar permutaciones!
Entonces, de las\(13,800\) formas de seleccionar a\(3\) las personas\(25\), seis de ellas involucran a Abe, Bea y Cindy. El mismo argumento funciona para cualquier otro grupo de tres personas (digamos Abe, Bea y David o Frank, Gloria e Hildy) por lo que cada grupo de tres personas se cuenta seis veces. Así la\(13,800\) cifra es seis veces demasiado grande. El número de grupos distintos de tres personas será\(\dfrac{13,800}{6} = 2300\).
Podemos generalizar la situación en este ejemplo anterior a cualquier problema de elegir una colección de artículos sin reemplazo donde el orden de selección no sea importante. Si estamos eligiendo\(r\) ítems fuera de\(n\) posibilidades (en lugar de 3 sobre 25 como en los ejemplos anteriores), el número de opciones posibles vendrá dado por\(\dfrac{_nP_r}{_rP_r}\), y podríamos usar esta fórmula para el cálculo. Sin embargo, esta situación surge con tanta frecuencia que le damos una notación especial y una definición especial a esta situación en la que estamos eligiendo\(r\) artículos fuera de\(n\) posibilidades sin reemplazo donde el orden de selección no es importante.
\[_nC_r = \dfrac{_nP_r}{_rP_r} \nonumber \]
Decimos que hay\(_nC_r\) combinaciones de tamaño\(r\) que se pueden seleccionar entre\(n\) opciones sin reemplazo donde el orden no importa. También podemos escribir la fórmula de combinaciones en términos de factoriales:
\[_nC_r = \dfrac{n!}{(n-r)!r!} \nonumber \]
Se elegirá un grupo de cuatro alumnos de una clase de 35 miembros para representar a la clase en el consejo estudiantil. ¿De cuántas maneras se puede hacer esto?
Solución
Ya que estamos eligiendo 4 personas de cada 35 sin reemplazo donde el orden de selección no es importante hay\(_{35}C_4 = \dfrac{35 \cdot 34 \cdot 33 \cdot 32}{4 \cdot 3 \cdot 2 \cdot 1} = 52,360\) combinaciones.
El Comité de Apropiaciones del Senado de Estados Unidos está integrado por 29 integrantes; el Subcomité de Defensa del Comité de Apropiaciones está integrado por 19 Sin tener en cuenta la afiliación partidista o cualquier escaño especial en el Subcomité, ¿cuántas subcomisiones diferentes de 19 miembros pueden elegirse de entre los 29 Senadores de la Comisión de Apropiaciones?
En el anterior problema Pruébalo Ahora, asumimos que los 19 integrantes del Subcomité de Defensa fueron elegidos sin tener en cuenta la afiliación partidista. En realidad esto nunca sucedería: si los republicanos son mayoritarios nunca dejarían que una mayoría de demócratas se sentara en (y así controlaran) cualquier subcomité. (Lo mismo, por supuesto, sería cierto si los demócratas estuvieran en control). Entonces, volvamos a considerar el ejemplo, de una forma un poco más complicada.
El Comité de Apropiaciones del Senado de Estados Unidos está integrado por 29 miembros, 15 republicanos y 14 demócratas. El Subcomité de Defensa está integrado por 19 integrantes, 10 republicanos y 9 demócratas. ¿De cuántas maneras diferentes pueden elegirse los integrantes del Subcomité de Defensa de entre los 29 Senadores de la Comisión de Apropiaciones?
Solución
En este caso, tenemos que elegir a 10 de los 15 republicanos y a 9 de los 14 demócratas. Hay\(_{15}C_{10} = 3003\) formas de elegir a los 10 republicanos y\(_{14}C_{9} = 2002\) formas de elegir a los 9 demócratas. ¿Pero ahora qué? ¿Cómo terminamos el problema?
Supongamos que enumeramos todos los posibles grupos republicanos de 10 miembros en 3003 hojas de papel rojo y todos los posibles grupos demócratas de 9 miembros en hojas de papel azul de 2002. ¿De cuántas maneras podemos elegir un slip rojo y un slip azul? ¡Este es un trabajo para la Regla de Conteo Básico! Simplemente estamos haciendo una elección de la primera categoría y una elección de la segunda categoría, al igual que en los problemas de menú del restaurante de antes.
Debe haber\(3003 \cdot 2002 = 6,012,006\) posibles formas de seleccionar a los integrantes del Subcomité de Defensa.
Probabilidad usando permutaciones y combinaciones
Podemos usar permutaciones y combinaciones para ayudarnos a responder preguntas de probabilidad más complejas
Se selecciona un número PIN de 4 dígitos. ¿Cuál es la probabilidad de que no haya dígitos repetidos?
Solución
Hay 10 valores posibles para cada dígito del PIN (a saber: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), por lo que hay números PIN\(10 \cdot 10 \cdot 10 \cdot 10 = 104 = 10,000\) totales posibles.
Para no tener dígitos repetidos, los cuatro dígitos tendrían que ser diferentes, lo que es seleccionar sin reemplazo. Podríamos o computar\(10 \cdot 9 \cdot 8 \cdot 7\), o notar que esto es lo mismo que la permutación\(_{10}P_4 = 5040\).
La probabilidad de que no se repitan dígitos es el número de números PIN de 4 dígitos sin dígitos repetidos dividido por el número total de números PIN de 4 dígitos. Esta probabilidad es
\(\dfrac{_{10}P_4}{10^4} = \dfrac{5040}{10000} = 0.504\)
De ahí que exista un 50.4% de probabilidad de que el PIN de 4 dígitos no tenga dígitos repetidos.
En la lotería de cierto estado, 48 bolas numeradas del 1 al 48 se colocan en una máquina y seis de ellas se sortean al azar. Si los seis números sorteados coinciden con los números que un jugador había elegido, el jugador gana $1,000,000. En esta lotería, el orden en el que se sortean los números no importa. Calcule la probabilidad de que gane el premio del millón de dólares si compra un solo boleto de lotería.
Solución
Para calcular la probabilidad, necesitamos contar el número total de formas en que se pueden extraer seis números, y el número de formas en que los seis números en el boleto del jugador podrían coincidir con los seis números extraídos de la máquina. Dado que no hay estipulación de que los números estén en un orden en particular, el número de posibles resultados del sorteo de lotería es\(_{48}C_6 = 12,271,512\). De estos posibles resultados, solo uno coincidiría con los seis números del boleto del jugador, por lo que la probabilidad de ganar el gran premio es:
\(\dfrac{_{6}C_6}{_{48}C_6} = \dfrac{1}{12271512} ≈ 0.0000000815\)
Así, hay menos de un 1% de posibilidades de ganar el gran premio.
En la lotería estatal del ejemplo anterior, si cinco de los seis números sorteados coinciden con los números que un jugador ha elegido, el jugador gana un segundo premio de $1,000. Calcule la probabilidad de que gane el segundo premio si compra un solo boleto de lotería.
Solución
Como anteriormente, el número de posibles resultados del sorteo de lotería es\(_{48}C_6 = 12,271,512\). Para ganar el segundo premio, cinco de los seis números del boleto deben coincidir con cinco de los seis números ganadores; es decir, debemos haber elegido cinco de los seis números ganadores y uno de los 42 números perdedores. El número de formas de elegir 5 de los 6 números ganadores viene dado por\(_6C_5 = 6\) y el número de formas de elegir 1 de los 42 números perdedores viene dado por\(_{42}C_1 = 42\). Así, el número de resultados favorables viene dado entonces por la Regla de Conteo Básico:\(_6C_5 \cdot _{42}C_1 = 6 \cdot 42 = 252\). Entonces, la probabilidad de ganar el segundo premio es.
\(\dfrac{_{6}C_6}{_{48}C_6} = \dfrac{1}{12271512} ≈ 0.0000000815\)
Esto significa que hay menos de un 1% de posibilidades de ganar el segundo premio. ¡Guau! Ahora podemos ver por qué algunas personas lo llaman “suerte” al ganar la lotería porque las posibilidades de ganar son muy bajas.
Una pregunta de opción múltiple en un cuestionario de economía contiene 10 preguntas con cinco posibles respuestas cada una. Calcular la probabilidad de adivinar aleatoriamente las respuestas y obtener 9 preguntas correctas.
Calcula la probabilidad de sacar al azar cinco cartas de una baraja y obtener exactamente un As.
Solución
En muchos juegos de cartas (como el póquer) el orden en el que se roban las cartas no es importante (ya que el jugador puede reorganizar las cartas en su mano de la manera que elija); en los problemas que siguen, asumiremos que este es el caso a menos que se indique lo contrario. Así, utilizamos combinaciones para calcular el número posible de manos de 5 cartas,\(_{52}C_5\). Este número irá en el denominador de nuestra fórmula de probabilidad, ya que es el número de posibles resultados.
Para el numerador, necesitamos la cantidad de formas de sacar un As y otras cuatro cartas (ninguna de ellas Ases) de la baraja. Ya que hay cuatro Ases y queremos exactamente uno de ellos, habrá\(_4C_1\) formas de seleccionar un As; ya que hay 48 No Aces y queremos 4 de ellos, habrá 48C4 formas de seleccionar los cuatro No Aces. Ahora usamos la Regla de Conteo Básico para calcular que habrá\(_4C_1 \cdot _{48}C_4\) formas de elegir un as y cuatro no ases.
Armando todo esto, tenemos
\(P(\text{one Ace}) = \dfrac{(_{4}C_1)(_{48}C_4)}{(_{52}C_5)} = \dfrac{778320}{2598960} ≈ 0.299\)
Así, hay alrededor de un 30% de probabilidad de sacar exactamente un As en una mano de 5 cartas.
Calcula la probabilidad de sacar al azar cinco cartas de una baraja y obtener exactamente dos ases.
Solución
La solución es similar al ejemplo anterior, excepto que ahora estamos eligiendo 2 Ases de 4 y 3 no Aces de 48; el denominador sigue siendo el mismo:
\(P(\text{two Aces}) = \dfrac{(_{4}C_2)(_{48}C_3)}{(_{52}C_5)} = \dfrac{103776}{2598960} ≈ 0.0399\)
Hay alrededor de un 4% de probabilidad de sacar 2 Ases en una mano de 5 cartas. Observe del ejemplo 37, la probabilidad de dibujar exactamente un As es mucho mayor que dibujar dos.
Calcula la probabilidad de sacar al azar cinco cartas de una baraja de cartas y obtener tres ases y dos reyes.
Problema de cumpleaños
Hagamos una pausa para considerar un problema famoso en la teoría de la probabilidad:
Supongamos que tienes una habitación llena de 30 personas. ¿Cuál es la probabilidad de que haya al menos un cumpleaños compartido?
Adivina la respuesta al problema anterior. ¿Tu conjetura fue bastante baja, como alrededor del 10%? Esa parece ser la respuesta intuitiva (\(\dfrac{30}{365}\)¿quizás?). Veamos si debemos escuchar nuestra intuición. Empecemos con un problema más sencillo, sin embargo.
Supongamos que hay tres personas en una habitación. ¿Cuál es la probabilidad de que haya al menos un cumpleaños compartido entre estas tres personas?
Solución
Hay muchas maneras en que podría haber al menos un cumpleaños compartido. Afortunadamente, hay una manera más fácil. Nos preguntamos “¿Cuál es la alternativa a tener al menos un cumpleaños compartido?” En este caso, la alternativa es que no haya cumpleaños compartidos. En otras palabras, la alternativa a “al menos uno” es no tener ninguno. Es decir, al tratarse de un acontecimiento complementario,
\(P(\text{at least one}) = 1 – P(\text{none})\)
Comenzaremos, entonces, calculando la probabilidad de que no haya cumpleaños compartido. Imaginemos que eres una de estas tres personas. Tu cumpleaños puede ser cualquier cosa sin conflicto, así que hay 365 opciones de 365 para tu cumpleaños. ¿Cuál es la probabilidad de que la segunda persona no comparta tu cumpleaños? Hay 365 días en el año (ignoremos los años bisiestos) y quitando tu cumpleaños de la contienda, hay 364 opciones que te garantizarán que no compartas un cumpleaños con esta persona, por lo que la probabilidad de que la segunda persona no comparta tu cumpleaños es\(\dfrac{364}{365}\). Ahora nos trasladamos a la tercera persona. ¿Cuál es la probabilidad de que esta tercera persona no tenga el mismo cumpleaños que usted o la segunda persona? Son 363 días que no duplicarán tu cumpleaños ni el de la segunda persona, por lo que la probabilidad de que la tercera persona no comparta cumpleaños con los dos primeros es\(\dfrac{363}{365}\).
Queremos que la segunda persona no comparta un cumpleaños contigo y la tercera persona no comparta un cumpleaños con las dos primeras personas, así que usamos la regla de multiplicación:
\(P(\text{no shared birthday}) = \dfrac{365}{365} \cdot \dfrac{364}{365} \cdot \dfrac{363}{365} ≈ 0.9918 \)
y luego restar de 1 para obtener
\(P(\text{shared birthday}) = 1 – P(\text{no shared birthday}) = 1 – 0.9918 = 0.0082\)
Esto significa que hay menos de un 1% de probabilidad de que una persona en una habitación de 3 tenga al menos un cumpleaños compartido.
Este es un número bastante pequeño, así que tal vez tenga sentido que la respuesta a nuestro problema original sea pequeña. Hagamos que nuestro grupo sea un poco más grande.
Supongamos que cinco personas están en una habitación. ¿Cuál es la probabilidad de que haya al menos un cumpleaños compartido entre estas cinco personas?
Solución
Continuando con el patrón del ejemplo anterior, la respuesta debería ser
\(P(\text{shared birthday}) = 1 – \dfrac{365}{365} \cdot \dfrac{364}{365} \cdot \dfrac{363}{365} \cdot \dfrac{362}{365} \cdot \dfrac{361}{365} ≈ 0.0271\)
Tenga en cuenta que podríamos reescribir esto de manera más compacta como
\(P(\text{shared birthday}) = 1 – \dfrac{_{365}P_5}{365^5} ≈ 0.0271\)
lo que hace que sea un poco más fácil escribir en una calculadora o computadora, y que sugiere una buena fórmula a medida que continuamos expandiendo la población de nuestro grupo.
Supongamos que hay 30 personas en una habitación. ¿Cuál es la probabilidad de que haya al menos un cumpleaños compartido entre estas 30 personas?
Solución
Aquí podemos calcular
\(P(\text{shared birthday}) = 1 – \dfrac{_{365}P_{30}}{365^{30}} ≈ 0.706\)
lo que nos da el sorprendente resultado de que cuando estás en una habitación con 30 personas hay un 70% de posibilidades de que haya al menos un cumpleaños compartido.
Si te gusta apostar, y si puedes convencer a 30 personas para que revelen sus cumpleaños, es posible que puedas ganar algo de dinero apostando a un amigo que habrá al menos dos personas con el mismo cumpleaños en la habitación cada vez que estés en una habitación de 30 o más personas. (Por supuesto, ¡tendrías que asegurarte de que tu amigo no haya estudiado la probabilidad!) No tendrías la garantía de ganar, pero deberías ganar más de la mitad del tiempo.
Este es uno de los muchos resultados en la teoría de la probabilidad que es contraintuitiva; es decir, va en contra de nuestros instintos intestinales. Si aún no crees en las matemáticas, puedes llevar a cabo una simulación. Sólo para que no tengas que ir por ahí redondeando grupos de 30 personas, alguien amablemente ha desarrollado un applet Java para que puedas realizar una simulación por computadora. Ir a esta página web: http://www-stat.stanford.edu/~susan/... /Birthday.html, y una vez que se haya cargado el applet, seleccione 30 cumpleaños y luego siga haciendo clic en Inicio y Restablecer. Si haces un seguimiento del número de veces que hay un cumpleaños repetido, deberías recibir un cumpleaños repetido aproximadamente 7 de cada 10 veces que ejecutes la simulación.
Supongamos que 10 personas están en una habitación. ¿Cuál es la probabilidad de que haya al menos un cumpleaños compartido entre estas 10 personas?


