1.2: ¿Problema o ejercicio?
- Page ID
- 112789
La principal actividad de las matemáticas es resolver problemas. Sin embargo, lo que la mayoría de la gente experimenta en la mayoría de las aulas de matemáticas son Un ejercicio es diferente de un problema.
En un problema, probablemente no sepas al principio cómo abordarlo para resolverlo. No se sabe qué ideas matemáticas podrían usarse en la solución. Parte de resolver un problema es entender lo que se pide, y saber cómo debería ser una solución. Los problemas a menudo involucran arranques en falso, cometer errores y ¡mucho papel rascar!
En un ejercicio, a menudo estás practicando una habilidad. Es posible que hayas visto a un maestro demostrar una técnica, o puedes haber leído un ejemplo trabajado en el libro. Luego practicas en asignaciones muy similares, con el objetivo de dominar esa habilidad.
Lo que es un problema para algunas personas puede ser un ejercicio para otras personas que tienen más conocimientos de fondo! Para un estudiante joven que acaba de aprender además, esto podría ser un problema:
\[\textit{Fill in the blank to make a true statement} \: \_\_\_ + 4 = 7 \ldotp \nonumber \]
Pero para ti, ¡eso es un ejercicio!
Tanto los problemas como los ejercicios son importantes en el aprendizaje de las matemáticas. Pero nunca debemos olvidar que el objetivo final es desarrollar más y mejores habilidades (a través de ejercicios) para que podamos resolver problemas más difíciles e interesantes.
Aprender matemáticas es un poco como aprender a practicar un deporte. Puedes practicar muchas habilidades:
- golpeando cientos de derechas en el tenis para que los puedas colocar en un lugar determinado de la cancha,
- descomponer los trazos en las piezas componentes en la natación para que cada parte del trazo sea más eficiente,
- mantener el control de la pelota mientras se hacen giros rápidos en el fútbol,
- tiros libres en básquetbol,
- atrapar pelotas de alta mosca en béisbol,
y así sucesivamente.
Pero el objetivo del deporte es jugar el juego. Practicas las habilidades para que seas mejor jugando el juego. En matemáticas, ¡resolver problemas es jugar el juego!
Por su cuenta
Para cada pregunta a continuación, decida si es un problema o un ejercicio. (¡No necesitas resolver los problemas! Simplemente decida qué categoría se ajusta para usted.) Después de haber etiquetado cada una, compara tus respuestas con un compañero.
- Este reloj se ha roto en tres piezas. Si agrega los números en cada pieza, las sumas son números consecutivos. (Nota: Los números consecutivos son números enteros que aparecen uno tras otro, como 1, 2, 3, 4 o 13, 14, 15.)
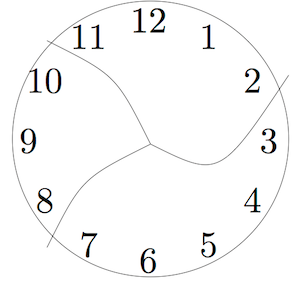
¿Se puede romper otro reloj en un número diferente de piezas para que las sumas sean números consecutivos? Supongamos que cada pieza tiene al menos dos números y que ningún número está dañado (por ejemplo, 12 no se divide en dos dígitos 1 y 2).
- Un entrenador de futbol comenzó el año con un presupuesto de $500. A finales de diciembre, el entrenador gastó 450 dólares. ¿Cuánto dinero en el presupuesto no se gastó?
- ¿Cuál es el producto de 4,500 y 27?
- Organice los dígitos 1—6 en un “triángulo de diferencia” donde cada número en la fila de abajo es la diferencia de los dos números por encima de él.
- Simplifica la siguiente expresión: $$\ frac {2 + 2 (5^ {3} - 4^ {2}) ^ {5} - 2^ {2}} {2 (5^ {3} - 4^ {2})}\ ldotp$$
- ¿Cuál es la suma de\(\frac{5}{2}\) y\(\frac{3}{13}\)?
- Tienes ocho monedas y una balanza. Las monedas se parecen, pero una de ellas es una falsificación. La moneda falsificada es más ligera que las demás. Solo puedes usar la balanza dos veces. ¿Cómo puedes encontrar la moneda falsificada?

- ¿Cuántas casillas, de cualquier tamaño posible, hay en un tablero de ajedrez estándar de 8 × 8?
- ¿Qué número es 3 más de la mitad de 20?
- Encuentra el número de ocho dígitos más grande compuesto por los dígitos 1, 1, 2, 2, 3, 3, 4 y 4 de tal manera que los 1 están separados por un dígito, los 2 están separados por dos dígitos, los 3 por tres dígitos, y los 4 por cuatro dígitos.

