2.3: Números binarios

Última actualización
Guardar como PDF

Page ID: 112728

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Volvamos a la regla 1← 2 y examinemos lo que realmente está pasando.

La Regla 1← 2

Siempre que hay dos puntos en una sola caja, “explotan”, desaparecen y se convierten en un punto en la caja a la izquierda.

Dos puntos en el cuadro más a la derecha vale un punto en el siguiente cuadro a la izquierda.

$binary1-300x39.png$

Si cada uno de los puntos originales vale “uno”, entonces el punto único de la izquierda debe valer dos.

$binary2-300x51.png$

Pero también tenemos dos puntos en el cuadro de valor 2 vale un punto en el cuadro justo a la izquierda...

$binary3-300x56.png$

Así que esa siguiente caja debe valer dos 2's, ¡que es cuatro!

$binary4-300x52.png$

Y dos de estas cuatro patas hacen ocho.

$binary5-300x51.png$

Dijimos antes que el código 1← 2 para nueve puntos era 1001. Comprobemos:

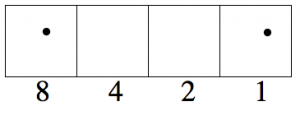
$binary6-300x120.png$

\[8 + 1 = 9 \nonumber \]

¡así que esto funciona!

Debió haber encontrado que diez puntos tiene 1← 2 código 1010.

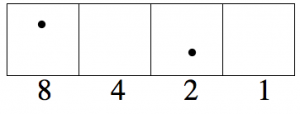
$binary7-300x114.png$

¡Sí!

\[8 + 2 = 10 \ldotp \nonumber \]

Problema 7

Si hubiera una caja a la izquierda de la casilla 8, ¿cuál sería el valor de esa caja?
¿Cuál sería el valor de una caja dos spots a la izquierda de la casilla 8? ¿Tres puntos a la izquierda?
¿Qué número tiene 1← 2 código 100101?
¿Cuál es el código 1← 2 para doscientos puntos?

Definición y Notación

Los números escritos en el código 1← 2 se denominan números binarios o números base dos. (El prefijo “bi” significa “dos”.)

A partir de ahora, cuando queramos indicar que un número está escrito en la base dos, escribiremos un subíndice “dos” en el número.

Entonces$1001_{two}$ significa “el número de puntos que tiene 1← 2 código 1001”, que ya vimos era nueve.

¡Importante! Cuando leemos decimos “uno cero cero una base dos”. No decimos “mil uno”, porque “mil” no es un número binario.

Pensar/Parejar/Compartir

Tu primer objetivo: idear un método general para encontrar el número de puntos representados por cualquier número binario. Describa claramente su método. Pon a prueba tu método en estos números y comprueba tu trabajo “sin explotar” los puntos. $$1_ {dos}\ qquad 101_ {dos}\ qquad 1011_ {dos}\ qquad 1111_ {dos}\ qquad 11111_ {dos} $$
Explica por qué los números binarios solo contienen los dígitos 0 y 1.
Aquí hay un nuevo objetivo (más difícil): idear un método general para encontrar el número binario relacionado con cualquier número de puntos sin pasar realmente por el proceso de “punto explosivo”. Describa claramente su método. Pon a prueba tu método en estos números y encuentra la manera de revisar tu trabajo.

dos puntos = ___ _dos diecisiete puntos = ___ _dos

_{sesenta y tres puntos = ___ doscientos puntos = ___ _dos}

Historia

Probablemente ya te des cuenta de que un número es un concepto abstracto con muchas representaciones. La representación decimal estándar de un número es sólo una de estas. Para las computadoras, los números siempre se representan en binario. Las unidades básicas son transistores que están encendidos (1) o apagados (0).

$electronic-circuit-board-300x258.jpg$

Placa de circuito electrónico de Samsung Galaxy S III.

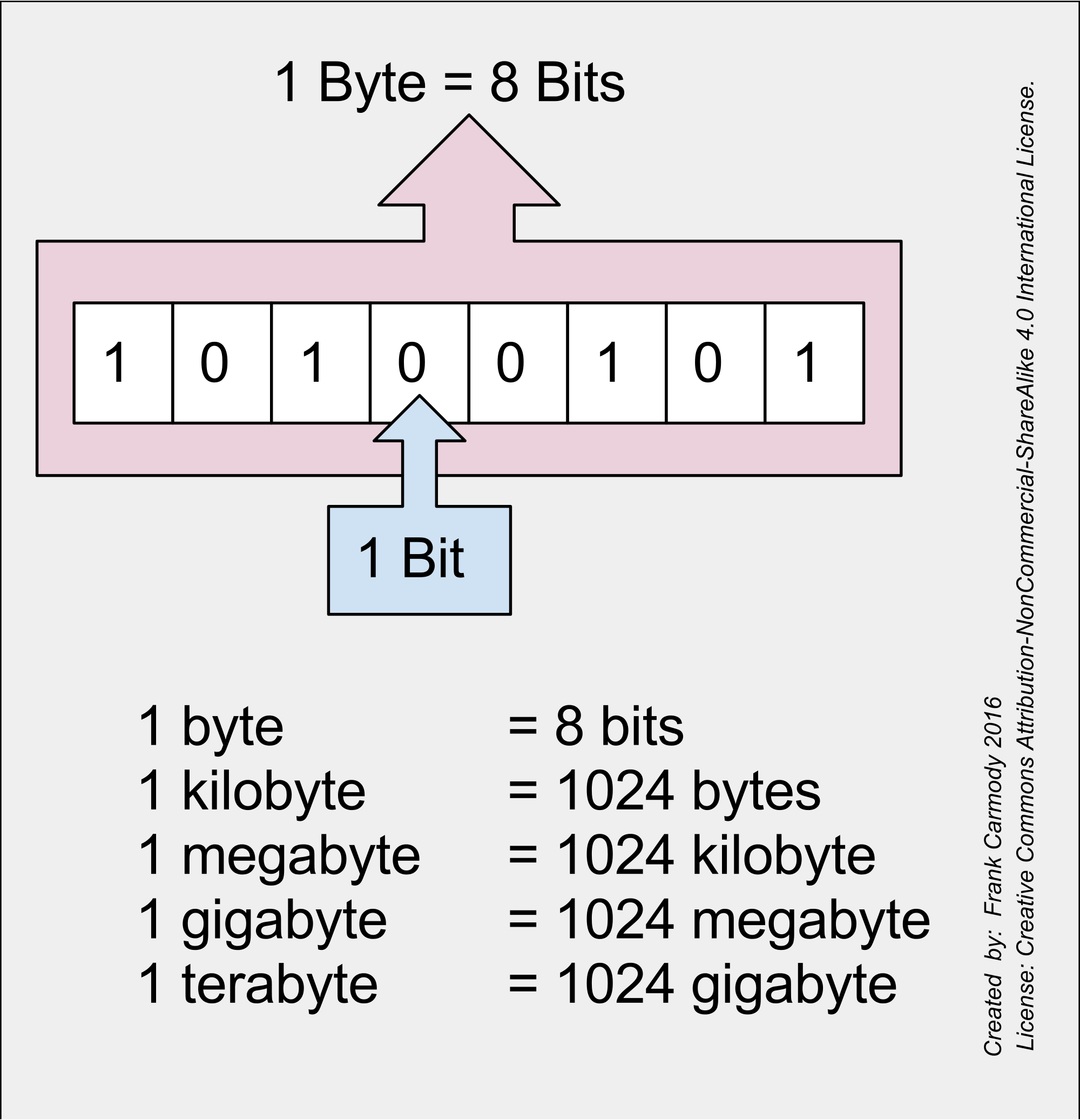
$2000px-bits_and_bytes.svg_.png$

Se dice que un transistor ^[1] almacena un bit de información. Ocho bits forman un byte y la unidad de procesamiento central de una computadora doméstica típica realiza cálculos en registros que son cada uno de 8 bytes (64 bits).

Usando la regla 1← 2 podemos representar los números del 0 al 18,446,744,073,709,551,615 con 64 bits.

Imagen de placa de circuito de http://www.publicdomainpictures.net/, licenciada bajo CC0 Public Domain.