2.4: Otras Bases
- Page ID
- 112699
En el sistema 1← 3, tres puntos en una caja vale un punto en el cuadro un punto a la izquierda. Esto da una nueva imagen:

Cada punto en el segundo cuadro de la izquierda vale tres. Cada punto en la tercera caja vale tres 3's, que es nueve, y así sucesivamente.
Dijimos que el código 1← 3 para quince es 120. Vemos que esto es correcto porque:
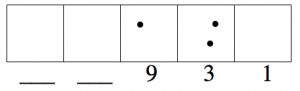
\[1 \cdot 9 + 2 \cdot 3 + 0 \cdot 1 = 15 \ldotp \nonumber \]
Responde estas preguntas sobre el sistema 1← 3.
- ¿Qué etiqueta debe ir en la caja a la izquierda de la caja 9?
- ¿Cuál sería el valor de una caja dos spots a la izquierda de la casilla 9?
- ¿Qué número tiene 110×3 código 21002?
- ¿Cuál es el código 1← 3 para doscientos puntos?
En el sistema 1← 4, cuatro puntos en una caja valen un punto en el cuadro un lugar a la izquierda.

Responde estas preguntas sobre el sistema 1← 4.
- ¿Cuál es el valor de cada caja en la imagen de arriba?
- ¿Cuál es el código 1← 4 para veintinueve puntos?
- ¿Qué número tiene 110×4 código 132?
En el sistema 1← 10, diez puntos en una caja valen un punto en la caja un lugar a la izquierda.
- Dibuja una imagen del 1← 10 y etiquete las primeras cuatro cajas con sus valores.
- ¿Cuál es el código 1← 10 para ocho mil cuatrocientos veintidós?
- ¿Qué número tiene 1← 10 código 95,753?
- Cuando escribimos el número 7.842, ¿qué representa el “7”?
El “4” son cuatro grupos de qué valor?
El “8” son ocho grupos de qué valor?
El “2” son dos grupos de qué valor? - ¿Por qué crees que utilizamos el sistema 1 ← 10 para escribir números?
Recordemos que los números escritos en el sistema 1← 2 se denominan números binarios o base dos.
Los números escritos en el sistema 1← 3 se denominan números base tres.
Los números escritos en el sistema 1← 4 se denominan números base cuatro.
Los números escritos en el sistema 1← 10 se denominan números base diez.
En general, los números escritos en el sistema 1← b se denominan números base b.
En un sistema de números base b, cada lugar representa una potencia de b, lo que significa\(b^{n}\) para algún número entero n. Recuerde que esto significa b multiplicado por sí mismo n veces:
- El lugar más a la derecha es el lugar de las unidades o unas. (¿Por qué es esto un poder de b?)
- El segundo lugar es el lugar “b”. (En la base diez, es el lugar de las decenas.)
- El tercer lugar es el “\(b^{2}\)” lugar. (En la base diez, ese es el lugar de los cientos. Tenga en cuenta que\(10^{2} = 100\).)
- El cuarto lugar es el “\(b^{3}\)” lugar. (En la base diez, ese es el lugar de miles, ya que\(10^{3} = 1000\).)
- Y así sucesivamente.
Siempre que estamos tratando con números escritos en diferentes bases, usamos un subíndice para indicar la base para que no pueda haber confusión. Entonces:
- \(102_{three}\)es un número base tres (léelo como “uno-cero-dos base tres”). Este es el código base tres para el número once.
- \(222_{four}\)es un número base cuatro (léelo como “dos-dos-dos base cuatro”). Este es el código base cuatro para el número cuarenta y dos.
- \(5321_{ten}\)es un número base diez. (Está bien decir “cincuenta y cuatro mil trescientos veintiuno”. ¿Por qué?)
Si la base no está escrita, asumimos que es la base diez.
Recuerda: cuando veas el subíndice, estás viendo el código para algún número de puntos.
- Encuentra el número de puntos representados por cada uno de estos: $$222_ {tres}\ qquad 310_ {four}\ qquad 5321_ {diez}\ ldotp$$
- Representan nueve puntos en cada base: $$\ text {tres, cinco, ocho, nueve y once}\ ldotp$$
- ¿Qué dígitos se utilizan en el sistema base dos? ¿El sistema base tres? ¿El sistema base cuatro? ¿El sistema base cinco? ¿El sistema base seis? ¿El sistema base diez?
- ¿Qué te dice la base sobre el sistema de números? (¡Piensa en tantas respuestas como puedas!)
Base b a Base Diez
Ahora vamos a describir algunos métodos generales para convertir de base b a base diez, donde b puede representar cualquier número entero mayor que uno.
Si la base es b, eso significa que estamos en un sistema 1← b. Un punto en la caja derecha- la mayoría vale 1. Un punto en la segunda caja vale b. Un punto en la tercera caja vale, y así sucesivamente.
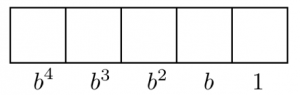
Entonces, por ejemplo, el número\(10123_{b}\) representa
\[1 \cdot b^{4} + 0 \cdot b^{3} + 1 \cdot b^{2} + 2 \cdot b + 3 \cdot 1, \nonumber \]
porque imaginamos tres puntos en el cuadro más a la derecha (cada uno vale uno), dos puntos en el segundo cuadro (cada uno representando b puntos), un punto en el tercer cuadro (representando\(b^{2}\) puntos), y así sucesivamente. Eso significa que solo podemos hacer un breve cálculo para encontrar el número total de puntos, sin pasar por toda la molestia de dibujar el cuadro y “desexplotar” los puntos.
Esto representa el número\[1 \cdot 5^{2} + 2 \cdot 5 + 3 = 25 + 10 + 3 = 38 \ldotp \nonumber \]
\[1 \cdot 7^{2} + 2 \cdot 7 + 3 = 49 + 14 + 3 = 66 \nonumber \]
Base Diez a Base b
Ahora vamos a describir algunos métodos generales para convertir de la base diez a la base b, donde b puede representar cualquier número entero mayor que uno.
Existen dos métodos generales para hacer estas conversiones. Para cada método, elaboraremos un ejemplo, y luego describiremos el método general. El primer método que describimos rellena las casillas de izquierda a derecha.
Convertir\(321_{ten}\) a un número base cinco (sin pasar realmente por el tedioso proceso de explotar puntos en grupos de cinco).
Encuentra la mayor potencia de cinco que es menor que 321. Solo enumeraremos poderes de cinco:
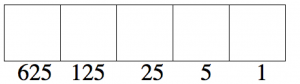
Entonces sabemos que la caja más a la izquierda que usaremos es la caja 125, porque 625 es demasiado grande.
¿Cuántos puntos habrá en la caja de 125? Eso es lo mismo que preguntar cuántos 125 hay en 321. Desde
\[2 \cdot 125 = 250 \qquad and \qquad 3 \cdot 125 = 375, \nonumber \]
deberíamos poner dos puntos en la caja de 125. Tres puntos serían demasiado.
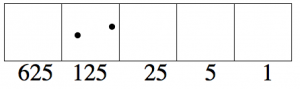
¿Cuántos puntos quedan descontabilizados? \(321 - 250 = 71\)quedan puntos.
Ahora repita el proceso: El mayor poder de cinco que es menos de 71 es\(5^{2} = 25\). Si ponemos dos en la caja de 25, eso cuida 50 puntos. (Tres puntos serían 75, lo que es demasiado.)
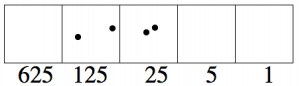
Hasta el momento tenemos dos puntos en la\(5^{3}\) caja y dos puntos en la\(5^{2}\) caja, así que eso es un total de
\[2 \cdot 125 + 2 \cdot 25 = 300\; \text{dots} \ldotp \nonumber \]
Nos quedan\(321 - 300 = 21\) puntos por dar cuenta.
Repite de nuevo el proceso: El mayor poder de 5 que es menos de 21 es 5. ¿Cuántos puntos pueden ir en la caja de 5? \(5 \cdot 4 = 20\), así podemos poner cuatro puntos en la caja de 5.
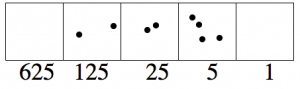
Nos queda un punto para dar cuenta. Si ponemos un punto en la caja 1, ya terminamos.
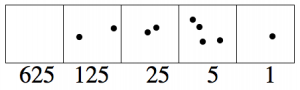
\[2 \cdot 125 + 2 \cdot 25 + 4 \cdot 5 + 1 = 250 + 50 + 20 + 1 = 321 \ldotp \nonumber \]
Entonces\(321_{ten} = 2241_{five} \ldotp\)
El algoritmo general para convertir de base diez a base:
- Comienza con tu base diez número n. Encuentra el mayor poder de b que sea menor que n, digamos que el poder es\(b^{k}\).
- Averigua cuántos puntos pueden ir en la\(b^{k}\) caja sin pasar por encima de n. Digamos que ese número es un. Pon el dígito a en la\(b^{k}\) caja, y luego resta\(n - a \cdot b^{k}\) para averiguar cuántos puntos quedan.
- Si tu número ahora es cero, has contabilizado todos los puntos. Pon ceros en las cajas que queden, y tienes el número. De lo contrario, empieza de nuevo en el paso (1) con el número de puntos que te quedan.
El método es un poco complicado de describir en completa generalidad. Probablemente sea mejor probar algunos ejemplos por tu cuenta para acostumbrarlo.
Utilice el método anterior para convertir\(99_{ten}\) a la base tres, a la base cuatro y a la base cinco.
Aquí hay otro método para convertir los números base diez a otra base, y este método rellena los dígitos de derecha a izquierda. Nuevamente, comenzaremos con un ejemplo y luego describiremos el método general.
Para convertir\(712_{ten}\) a un número base siete, imagina que hay 712 puntos en la caja unos. Escribiremos el número, pero imagínalo como puntos.
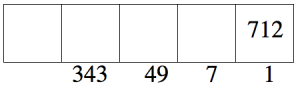
Averigua cuántos grupos de 7 puedes hacer, y cuántos puntos quedarían sobrantes.
\[712 \div 7 = 101\; \text{R}5 \; \qquad that\; is,\; 712 = 101 \cdot 7 + 5 \ldotp \nonumber \]
Eso significa que tenemos 101 grupos de 7 puntos, con 5 puntos sobrantes.
“Explotar” los grupos de 7 un cuadro a la izquierda, y dejar atrás los 5 puntos.
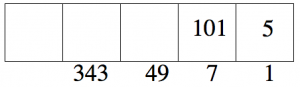
Ahora repite el proceso: ¿Cuántos grupos de 7 puedes hacer a partir de los 101 puntos?
\[101 \div 7 = 14\; \text{R}3, \qquad meaning\; 101 = 14 \cdot 7 + 3 \ldotp \nonumber \]
“Explotar” los grupos de 7 un cuadro a la izquierda, y dejar atrás los 3 puntos.
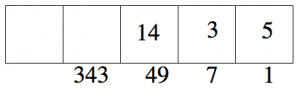
Repetir:
\[14 \div 7 = 2\; \text{R}0, \qquad so\; 14 = 2 \cdot 7 + 0 \ldotp \nonumber \]
“Explotar” los grupos de 7 un cuadro a la izquierda, y dejar 0 puntos atrás.
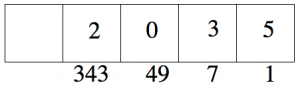
Ya que hay menos de 7 puntos en cada caja, ya terminamos.
\[712_{ten} = 2035_{seven} \ldotp \nonumber \]
Por supuesto, podemos (¡y debemos!) comprueba nuestro cálculo convirtiendo la respuesta de nuevo a la base diez:
\[2035_{seven} = 2 \cdot 7^{3} + 0 \cdot 7^{2} + 3 \cdot 7 + 5 = 686 + 0 + 21 + 5 = 712_{ten} \ldotp \nonumber \]
Así que aquí hay un segundo método general para convertir los números base diez a una base b arbitraria:
- Divide el número base diez por b para obtener un cociente y un resto.
- Poner el resto en el espacio más a la derecha en el número base b.
- Si el cociente es menor que b, va en el espacio un punto a la izquierda. De lo contrario, vuelve al paso (1) y repítelo con el cociente, rellenando los restos de derecha a izquierda en el número base.
Nuevamente, el método probablemente tenga más sentido si lo pruebas algunas veces.
Utilice el método descrito anteriormente para convertir\(250_{ten}\) a base tres, cuatro, cinco y seis.

