6.4: División y Decimales
- Page ID
- 112799
Cuando estudiabas fracciones, tenías muchas formas diferentes de pensar sobre ellas. Pero la primera forma, y a la que seguimos volviendo, es pensar en una fracción como la respuesta a un problema de división.
Supongamos que 6 tartas deben ser compartidas equitativamente entre 3 niños. Esto rinde 2 tartas por niño. Escribimos:
\[\frac{6}{3} = 2 \ldotp \nonumber \]
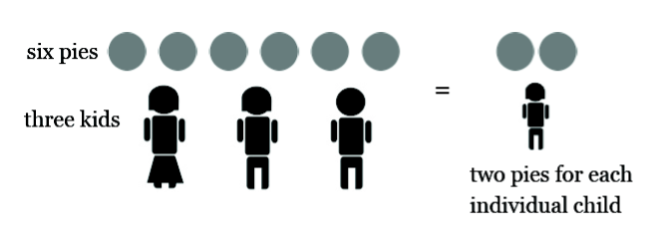
La fracción\(\frac{6}{3}\) equivale a la respuesta al problema de división\(6 \div 3 = 2\). Representa el número de tartas que recibe un niño entero.
De la misma manera...
compartir 10 tartas entre 2 niños rinde\(\frac{10}{2} = 5\) pasteles por niño,
compartir 8 tartas entre 2 niños rinde\(\frac{8}{2} = 4\) pasteles por niño,
compartir 5 pasteles entre 5 niños rinde\(\frac{5}{5} = 1\) pasteles por niño, y
la respuesta a compartir 1 tartas entre 2 niños es\(\frac{1}{2}\), que llamamos “la mitad”.
Asociamos el número “\(\frac{1}{2}\)” a la imagen
.
De la misma manera, el cuadro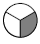
representa “un tercio”, es decir,\(\frac{1}{5}\).
(Esta es la cantidad de pastel que un niño individual recibiría si un pastel se comparte entre tres hijos).
La imagen
se llama “una quinta parte” y en efecto es\(\frac{1}{5}\), la cantidad de pastel que recibe un niño individual cuando un pastel es compartido por cinco niños.
Y la imagen
se llama “tres quintos” para representar\(\frac{3}{5}\), la cantidad de pastel que recibe un individuo si tres pasteles son compartidos por cinco niños.
Sabemos hacer división en nuestro modelo “Dots & Boxes”.
Supongamos que se le pide que compute\(3906 \div 3\). Una manera de interpretar esta pregunta (hay otras) es:
“¿Cuántos grupos de 3 caben en 3906?”
En nuestro modelo “Dots & Boxes”, el dividendo 3906 se ve así:
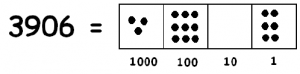
y tres puntos se ven así:
Así que realmente estamos preguntando:
“¿Cuántos grupos de caben en la imagen del 3906?”
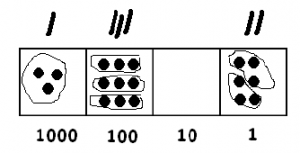
Observe lo que tenemos en la imagen:
- Un grupo de 3 en la caja de miles.
- Tres grupos de 3 en la caja de los cientos.
- Cero grupos de 3 en la caja de decenas.
- Dos grupos de 3 en la caja de unos.
Esto demuestra que 3 entra en 3906 mil, tres cientos y dos veces. Es decir,
\[3906 \div 3 = 1302 \ldotp \nonumber \]
Por supuesto, ¡no todos los problemas de división funcionan de manera uniforme! Aquí hay un ejemplo diferente.
Supongamos que se le pide que compute\(1024 \div 3\). Una forma de interpretar esta pregunta es:
“¿Cuántos grupos de 3 caben en 1024?”
Así que estamos buscando grupos de tres puntos en esta imagen:
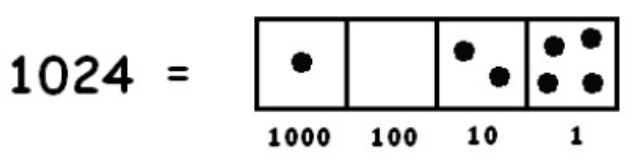
Un grupo de tres es fácil de detectar:
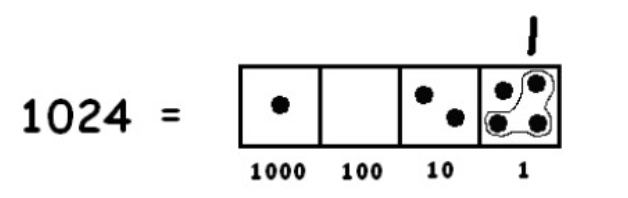
Para encontrar más grupos de tres puntos, debemos “desexplotar” un punto:
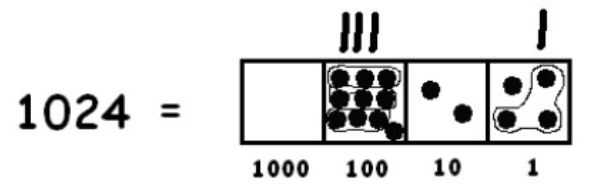
Tenemos que volver a desexplotar:
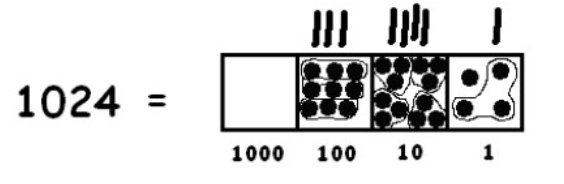
Esto deja un punto obstinado restante en la caja de unos y no más grupo de tres. Entonces concluimos:
\[1024 \div 3 = 341\; \text{R} 1,\; meaning\; 1024 = 341 \cdot 3 + 1 \ldotp \nonumber \]
En palabras: 1024 da 341 grupos de 3, más un punto extra.
Podemos juntar estas dos ideas —fracciones como respuesta a un problema de división y lo que sabemos sobre la división en el modelo “Puntos y cajas ”— para ayudarnos a pensar más sobre la conexión entre fracciones y decimales.
La fracción\(\frac{1}{8}\) es el resultado de dividir 1 por 8. De hecho, calculemos\(1 \div 8\) en un modelo de “Puntos y Cajas”, haciendo uso de decimales. Queremos encontrar grupos de ocho en la siguiente imagen:
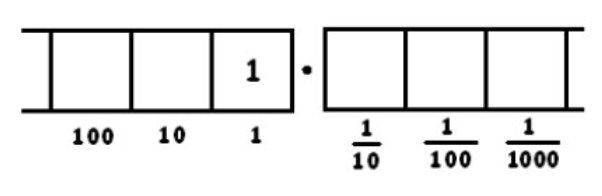
Claramente no se encuentra ninguno, así que no explotemos:
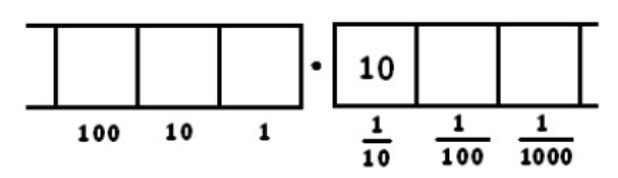
(Estamos siendo perezosos y no dibujando todos los puntos. A medida que siga, es posible que desee dibujar los puntos en lugar del número de puntos, si le ayuda a realizar un seguimiento).
Ahora hay un grupo de 8, dejando atrás a dos. Escribimos una marca en la parte superior, para hacer un seguimiento del número de grupos de 8, y dejar dos puntos atrás en la caja.
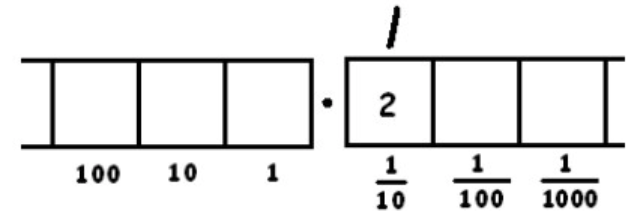
Podemos inexplotar los dos puntos de la\(\frac{1}{10}\) caja:
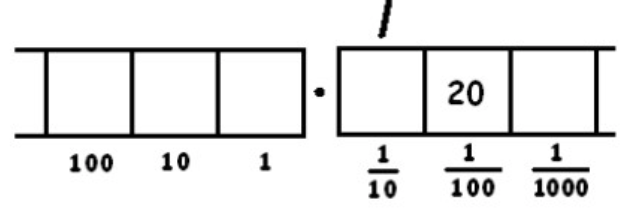
Esto da dos grupos de 8 dejando cuatro atrás. Recuerde: las dos marcas de verificación representan dos grupos de 8. Y quedan cuatro puntos en la\(\frac{1}{100}\) caja.
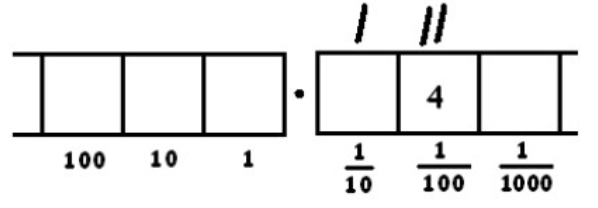
Sin explotar esos cuatro puntos restantes:
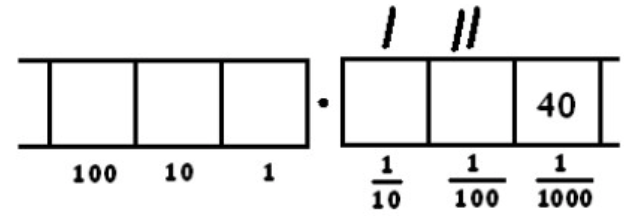
Ahora tenemos cinco grupos de 8 y ningún resto.
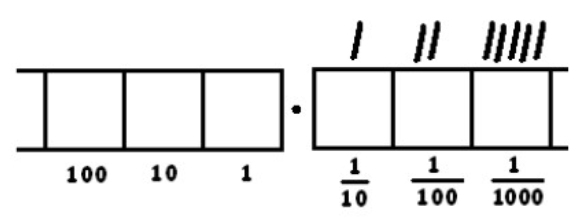
Recuerde: las marcas de verificación hicieron un seguimiento de cuántos grupos de ocho había en cada casilla. Tenemos
- Un grupo de 8 puntos en la\(\frac{1}{10}\) caja
- Dos grupos de 8 puntos en la\(\frac{1}{100}\) caja.
- Cinco grupos de 8 puntos en la\(\frac{1}{1000}\) caja.
Entonces concluimos que:
\[\frac{1}{8} = 1 \div 8 = 0.125 \ldotp \nonumber \]
Por supuesto, es un buen hábito comprobar nuestra respuesta:
\[0.125 = \frac{125}{1000} = \frac{5 \cdot 25}{5 \cdot 200} = \frac{5 \cdot 5}{5 \cdot 40} = \frac{5 \cdot 1}{5 \cdot 8} = \frac{1}{8} \ldotp \nonumber \]
Por su cuenta
Trabaja en los siguientes ejercicios por tu cuenta o con un compañero. Asegúrate de mostrar tu trabajo.
- Realizar la división en un modelo de “Puntos y Cajas” para mostrar que\(\frac{1}{4}\), como decimal, es\(0.25\).
- Realizar la división en un modelo de “Puntos y Cajas” para mostrar que\(\frac{1}{2}\), como decimal, es\(0.5\).
- Realizar la división en un modelo de “Puntos y Cajas” para mostrar que\(\frac{3}{5}\), como decimal, es\(0.6\).
- Realizar la división en un modelo de “Puntos y Cajas” para mostrar que\(\frac{3}{6}\), como decimal, es\(0.1875\).
- En términos más simples, ¿qué fracción está representada por cada uno de estos decimales? $$0.75,\ qquad 0.625,\ qquad 0.16,\ qquad 0.85,\ qquad 0.0625\ ldotp$$
Decimales repetidos
No todas las fracciones conducen a representaciones decimales simples.
Considera la fracción\(\frac{1}{3}\). Buscamos grupos de tres en el siguiente cuadro:
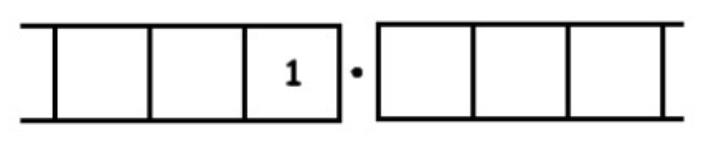
Inexplotar requiere que busquemos grupos de 3 en:
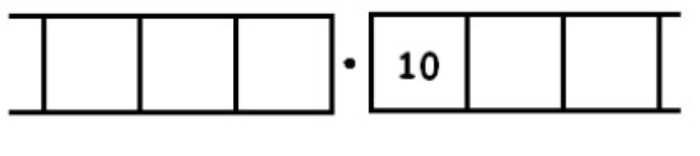
Aquí hay tres grupos de 3 dejando uno atrás:
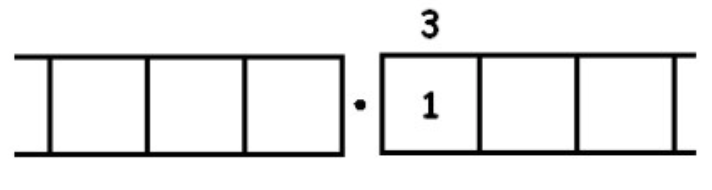
Sin explotar da:
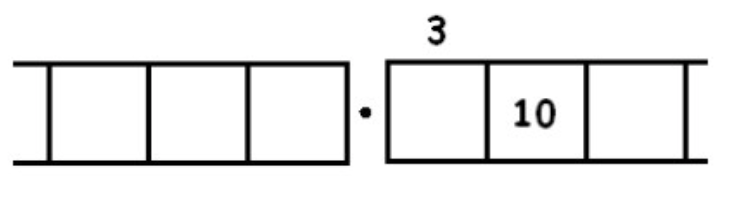
Nos encontramos con otros tres grupos de 3 dejando uno atrás:
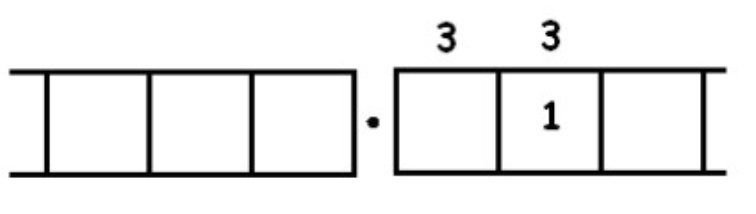
Sin explotar da:
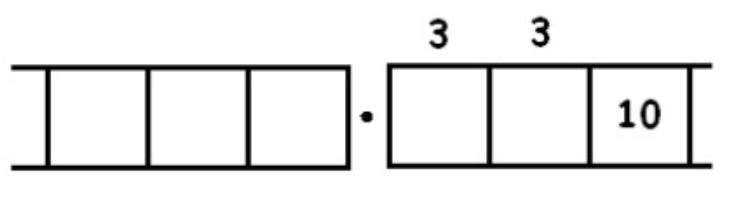
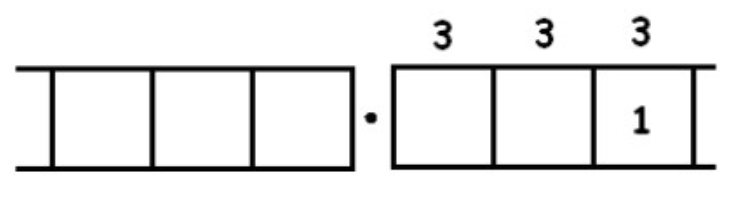
Y parece que estamos atrapados en un ciclo infinitamente repetitivo.
Ahora nos encontramos en una posición filosóficamente interesante. Como seres humanos, no podemos llevar a cabo esta, ni ninguna, actividad un número infinito de veces. Pero parece muy tentador escribir:
\[\frac{1}{3} = 0.33333 \ldots, \nonumber \]
con los puntos suspensivos “
” que significa “seguir para siempre con este patrón”. Podemos imaginar lo que esto significa, pero en realidad no podemos escribir esos infinitamente muchos 3 representados por el
Muchas personas hacen uso de un vinculum (barra horizontal) para representar decimales repetidos infinitamente largos. Por ejemplo,\(0. \bar{3}\) significa “repetir el 3 para siempre”:
\[0. \bar{3} = 0.33333 \ldots, \nonumber \]
y\(0.296 \overline{412}\) significa “repetir el 412 para siempre”:
\[0.296 \overline{412} = 0.296412412412412 \ldots \nonumber \]
Ahora estamos en condiciones de dar una respuesta quizás más satisfactoria a la pregunta\(1024 \div 3\). En el ejemplo anterior, encontramos que la respuesta es
\[1024 \div 3 = 341\; \text{R} 1 \ldotp \nonumber \]
Pero ahora sabemos que podemos seguir dividiendo ese último punto obstinado por 3. Recuerda, eso representa un solo punto en el lugar de unos, así que si seguimos dividiendo por tres realmente representa\(\frac{1}{3}\). Así que tenemos:
\[1024 \div 3 = 341\; \text{R} 1 = 341 \frac{1}{3} = 341.3333333 \ldots = 341. \bar{3} \ldotp \nonumber \]
Como otro ejemplo (más complicado), aquí está el trabajo que convierte la fracción\(\frac{6}{7}\) en un decimal repetitivo infinitamente largo. Asegúrate de entender los pasos de una línea a la siguiente.
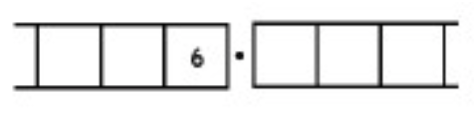
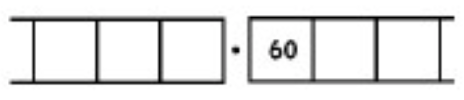
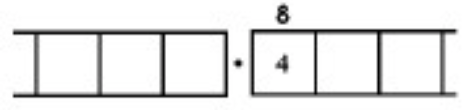
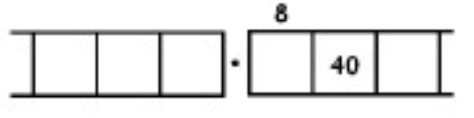
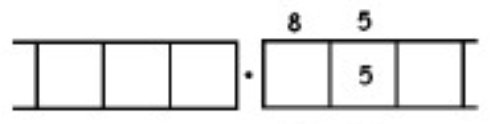
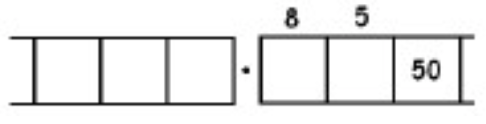
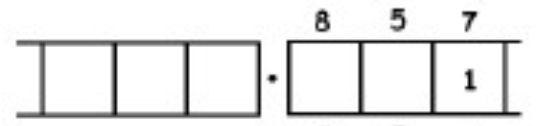
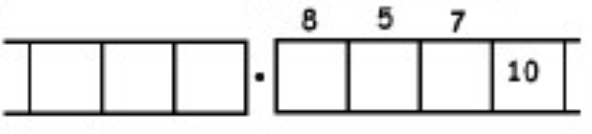
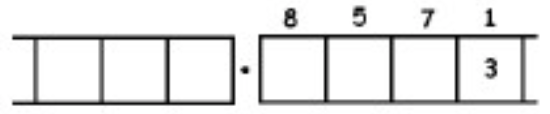
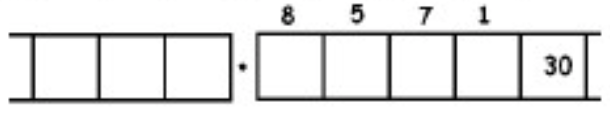
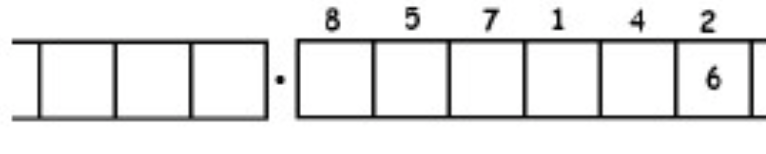
Con este 6 en el cuadro final más a la derecha, hemos vuelto al comienzo mismo del problema. (¿Ves por qué? Recuerda, ¡empezamos con un seis en la caja de los unos!)
Esto significa que simplemente repetiremos el trabajo que hemos realizado y obtendremos la misma secuencia de respuestas:\(857142\). Y luego otra vez, y luego otra vez, y luego otra vez. Contamos con:
\[\begin{split} \frac{6}{7} &= 0.857142857142857142857142 \ldots \\ &= 0. \overline{857142} \ldotp \end{split} \nonumber \]
Por su cuenta
Trabaja en los siguientes ejercicios por tu cuenta o con un compañero. Asegúrate de mostrar tu trabajo.
- Calcular\(\frac{4}{7}\) como un decimal repetitivo infinitamente largo.
- Calcular\(\frac{1}{9}\) como un decimal repetitivo infinitamente largo.
- Utilice un modelo de “Puntos y cajas” para calcular\(133 \div 6\). Escribe la respuesta como decimal.
- Utilice un modelo de “Puntos y cajas” para calcular\(255 \div 11\). Escribe la respuesta como decimal.