6.5: Más x -males
- Page ID
- 112803
No debería sorprendernos que también podamos usar este razonamiento sobre la división en el modelo “Dots & Boxes” en otras bases.
El siguiente cuadro muestra que trabajando en base 5
\[1432_{five} \div 13_{five} = 110_{five} R2_{five},\; \text{meaning}\; 1432_{five} = 110_{five} \cdot 13_{five} + 2_{five} \ldotp \nonumber \]
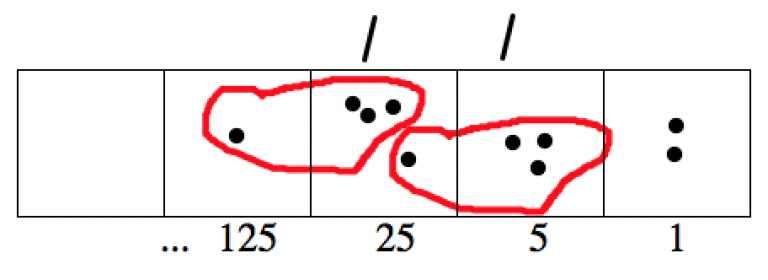
Explique cuidadosamente la conexión entre la imagen y la ecuación mostrada anteriormente.
- Mostrar en la imagen donde se ve\(1432_{five}\) de la ecuación.
- ¿Dónde ves\(13_{five}\)?
- ¿Dónde ves\(110_{five}\) y\(2_{five}\)?
Aquí es donde dejamos fuera de la división, con un resto de 2:
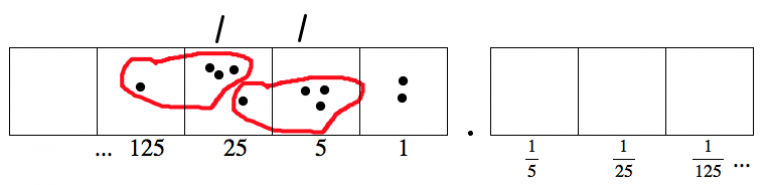
Ahora podemos inexplotar uno de esos dos puntos restantes. Entonces somos capaces de hacer otro grupo de\(13_{five}\).
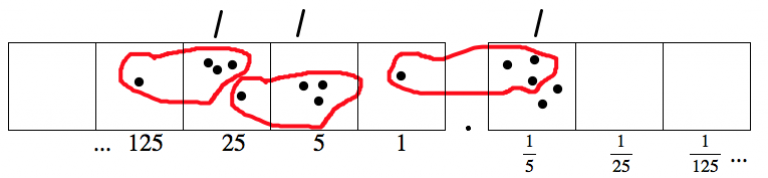
Una vez más, quedan dos puntos, no en ningún grupo. Así que vamos a inexplotar a uno de ellos.
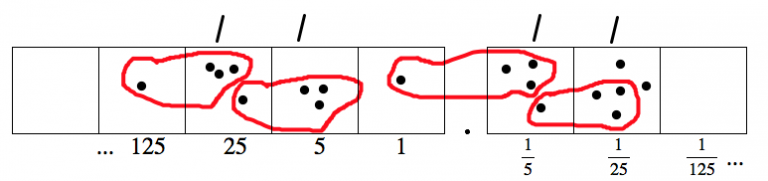
Y aún nos quedan dos puntos. ¿Por qué no volver a hacerlo?
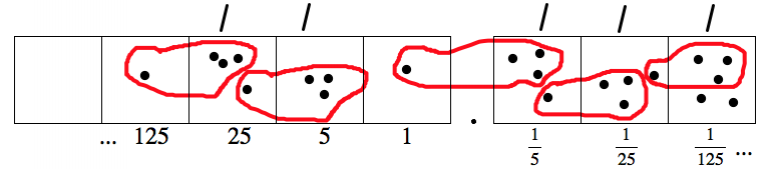
Parece que vamos a estar haciendo lo mismo para siempre:
- Comienza con dos puntos en alguna caja.
- Desexplota uno de los puntos, así que tienes un punto en tu caja original y cinco en la caja a la derecha.
- Formar un grupo de\(3_{five}\). Eso usa un punto en tu caja original y tres puntos en la caja a la derecha.
- Entonces te quedan dos puntos en una caja.
- Desexplota uno de los puntos, así que tienes un punto en tu caja original y cinco en la caja a la derecha.
- Esto se siente familiar...
Concluimos:
\[1432_{five} \div 13_{five} = 110.111 \ldots_{five} = 110. \bar{1}_{five} \ldotp \nonumber \]
La ecuación
\[1432_{five} \div 13_{five} = 110. \bar{1}_{five} \ldotp \nonumber \]
es una declaración en la base cinco. ¿Qué dice en la base diez?
“\(1432_{five}\)” es el número
\[1 \cdot 125 + 4 \cdot 25 + 3 \cdot 5 + 2 \cdot 1 = 242_{ten} \ldotp \nonumber \]
- ¿Qué hay\(13_{five}\) en la base 10? Asegúrese de explicar su respuesta.
- ¿Qué hay\(110. \bar{1}_{five}\) en la base 10? Explica cómo obtuviste tu respuesta.
- Traduzca la ecuación anterior a una sentencia en base diez y verifique que sea correcta.
- Dibuja imágenes para computar\(8 \div 3\) en un sistema base diez, y mostrar la respuesta es\(2. \bar{6}\).
- Dibuja las imágenes para calcular\(8_{nine} \div 3_{nine}\) en un sistema base 9, y escribe la respuesta como decimal. (¿O es un “nonimal”?)
- Dibuja las imágenes para computar\(1 \div 11\) en un sistema base diez, y mostrar la respuesta es\(0. \overline{09}\).
- Dibuja las imágenes base 3 para calcular\(1_{three} \div 11_{three}\), y escribe la respuesta como decimal (¿“trimal”?) número.
- Dibuja las cuatro imágenes base para calcular\(1_{four} \div 11_{four}\), y escribe la respuesta como decimal (¿“cuadrímico”?) número.
- Dibuja las imágenes base seis para calcular\(1_{six} \div 11_{six}\), y escribe la respuesta como decimal (¿“heximal”?) número.
- Describe cualquier patrón que notes en los cálculos anteriores. ¿Tienes una conjetura de una regla general? ¿Puedes probar que tu regla general es cierta?
Recuerda que la fracción\(\frac{2}{5}\) representa el problema de la división\(2 \div 5\). (Todo esto está escrito en base diez.)
- ¿Cuál es la expansión decimal (en base diez) de la fracción\(\frac{2}{5}\)?
- Reescribir la fracción de base diez\(\frac{2}{5}\) como un problema de división de base cuatro. Después encuentra la expansión decimal para esa fracción en la base cuatro.
- Reescribir la fracción de base diez\(\frac{2}{5}\) como un problema de división de base cinco. Después encuentra la expansión decimal para esa fracción en base cinco.
- Reescribir la fracción de base diez\(\frac{2}{5}\) como un problema de división de base siete. Después encuentra la expansión decimal para esa fracción en base siete.
- Barry dijo que en la base quince, el problema de la división parece $$2_ {quince}\ div 5_ {quince}, $$y la representación decimal sería\(0.6_{fifteen}\). Revisa la respuesta de Barry. ¿Tiene razón?
Expandir cada uno de los siguientes como un número “decimal” en la base dada. (La fracción se da en base diez.)
\[\begin{split} (a)\; \frac{1}{9}\; \text{in base 10} \quad \qquad &(b)\; \frac{1}{2}\; \text{in base 3} \\ (c)\; \frac{1}{3}\; \text{in base 4} \quad \qquad &(d)\; \frac{1}{4}\; \text{in base 5} \\ (e)\; \frac{1}{5}\; \text{in base 6} \quad \qquad &(f)\; \frac{1}{6}\; \text{in base 7} \\ (g)\; \frac{1}{7}\; \text{in base 8} \quad \qquad &(h)\; \frac{1}{8}\; \text{in base 9} \end{split} \nonumber \]
¿Notaste algún patrón? ¿Alguna conjetura?
¿Qué fracción tiene expansión decimal\(0. \bar{3}_{seven}\)? ¿Cómo sabes que tienes razón?