1.3: Conexiones Galois

Última actualización
Guardar como PDF

Page ID: 112190

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La preservación de las juntas y uniones, y en particular las cuestiones relativas a los efectos generativos, está estrechamente relacionada con la teoría de las conexiones Galois, lo que es un caso especial de una teoría más general que discutiremos más adelante, a saber, la de las adjunciones. Usaremos alguna terminología de amonestación al describir las conexiones de Galois.

Definición y ejemplos de conexiones Galois

Las conexiones de Galois entre preordenes fueron consideradas primero por Évariste Galois quien no las llamó con ese nombre en el contexto de una conexión que encontró entre “extensiones de campo” y “grupos de automorfismo”. No vamos a discutir esto más a fondo, pero la idea es que dados dos preordenes P y Q, una conexión Galois es un par de mapas de ida y vuelta de P a Q y de Q a P con ciertas propiedades, que la hacen como una versión relajada de isomorfismos. Para ser un poco más precisos, los isomorfismos de preorden son ejemplos de conexiones Galois, pero las conexiones de Galois no necesitan ser isomorfismos preordenados.

Definición: 1.95.

Una conexión Galois entre los preordenes P y Q es un par de mapas monótonos f: P → Q y g: Q → P tal que

f (p) ≤ q si y solo si p ≤ g (q) . (1.96)

Decimos que f es el colindante izquierdo y g es el colindante derecho de la conexión Galois.

Ejemplo 1.97.

Considera el mapa (3×−):$\mathbb{Z}$ →$\mathbb{R}$ que envía x$\in$$\mathbb{Z}$ a 3 x, que podemos considerar como un número real 3 x$\in$$\mathbb{Z}$$\subseteq$$\mathbb{R}$.

Busquemos un colindante izquierdo para el mapa (3 × −).

Escribe z para el número natural más pequeño por encima de z$\in$$\mathbb{R}$, y escribe z para el entero más grande debajo de z$\in$ R, por ejemplo, 3.14= 4 y 3.14= 3. $^{a}$Como la izquierda colindante$\mathbb{R}$ →$\mathbb{Z}$, veamos si −/3funciona.

Se comprueba fácilmente que

x /3 ≤ y si y solo si x ≤ 3 y.

¡Éxito! Así tenemos una conexión Galois entre −/3y (3 × −).

$^{a}$Por “arriba” y “abajo”, nos referimos a mayor o igual o menor o igual a; siendo este último un bocado. De todos modos, 3= 3 = 3.

Ejercicio 1.98.

En Ejemplo 1.97 encontramos un adjunto izquierdo para el monotonemap (3×−):$\mathbb{Z}$ →$\mathbb{R}$. Ahora encuentra un derecho adjunto para el mismo mapa, y muéstralo es correcto. ♦

Ejercicio 1.99.

Considera el preorden P = Q = 3.

1. Sea f, g los mapas monótonos que se muestran a continuación:

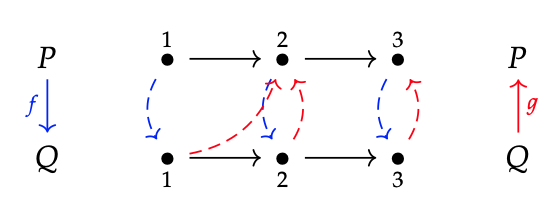
$Screen Shot 2021-01-05 en 2.40.51 PM.png$

¿Es el caso que f se deja colindante a g? Verifique que por cada 1 ≤ p, q ≤ 3, uno tenga f (p) ≤ q iff p ≤ g (q).

2. Sea f, g los mapas monótonos que se muestran a continuación:

3. ¿Es el caso que f se deja colindante a g? ♦

Obración 1.100. Las imágenes del Ejercicio 1.99 sugieren la siguiente idea. Si P y Q son órdenes totales y f: P → Q y g: Q → P se dibujan con flechas dobladas en sentido contrario a las agujas del reloj, entonces f se deja junto a g si las flechas no se cruzan. Con un poco de pensamiento, esto se puede formalizar. ¡Creemos que esta es una forma bastante ordenada de visualizar las conexiones de Galois entre los pedidos totales!

Ejercicio 1.101.

¿Tiene −/3una L colindante izquierda:$\mathbb{Z}$ →$\mathbb{R}$?
Si no, ¿por qué? Si es así, ¿su izquierda colindante tiene una izquierda colindante?

Volver a particiones

Recordemos del Ejemplo 1.52 que podemos entender el conjunto Prt (S) de particiones en un conjunto S en términos de funciones suryectivas fuera de S.

Supongamos que se nos da alguna función g: S → T. Mostraremos que esta función g induce una conexión Galois$g_{!}: \operatorname{Prt}(S) \leftrightarrows \operatorname{Prt}(T): g^{*}$, entre preorden de S -particiones y el preorden de T -particiones. La forma en que podrías explicarlo a un teórico de categoría experimentado es:

El colindante izquierdo se da sacando cualquier sobreyección de S y empujando hacia fuera a lo largo de g para obtener una sobreyección fuera de T. El colindante derecho se da tomando cualquier sobreyección de T, componiendo con g para obtener una función de S, y luego tomando la factorización epi-mono para obtener una sobrejección de S.

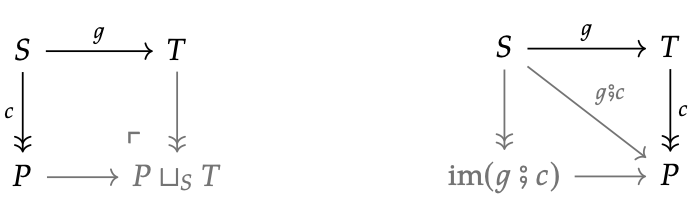
$Screen Shot 2021-01-05 en 2.44.33 PM.png$

Al final de este libro, el lector comprenderá los pushouts y las factorizaciones epi-mono, por lo que podrá darle sentido a la afirmación anterior. Pero por ahora vamos a explicar el proceso en términos más realista.

Comienza con g: S → T; primero queremos entender g! : Prt (S) → Prt (T). Así que empieza con una partición$_{∼S}$ de S. Para iniciar el proceso de obtención de una partición$_{∼T}$ en T, digamos que dos elementos$t_{1}$,$t_{2}$$\in$ T están en la misma parte$t_{1}$$_{∼T}$$t_{2}$,, si existe$s_{1}$,$s_{2}$$\in$ S con tal que$s_{1}$ ~s $s_{2}$y g ($s_{1}$) =$t_{1}$ y g (s 2) =$t_{2}$. Sin embargo, el resultado de hacerlo no necesariamente será transitivo, puede obtener$t_{1}$ ~T $t_{2}$y$t_{2}$ ~T $t_{3}$sin$t_{1} \sim_{T}^{?} t_{3}-$ y las particiones deben ser transitivas. Así que completa el proceso simplemente agregando las piezas faltantes (toma el cierre transitivo). El resultado es g! (∼ S) :=$_{∼T}$. Nuevamente comenzando con g, queremos conseguir el derecho adjunto g ∗: Prt (T) → Prt (S). Así que empieza con una partición$_{∼T}$ de T. Obtener una partición$_{∼S}$ en S diciendo que$s_{1}$$_{∼S}$$s_{2}$ iff g ($s_{1}$)$_{∼T}$ g ($s_{2}$). El resultado es g * ($_{~T}$) :=$_{~S}$.

Ejemplo 1.102.

Sea S = {1,2,3,4}, T = {12,3,4}, y g: S → T por g (1) := g (2) := 12, g (3) := 3, y g (4) := 4. La partición que se muestra a la izquierda a continuación se traduce por$g_{!}$ a la partición que se muestra a la derecha.

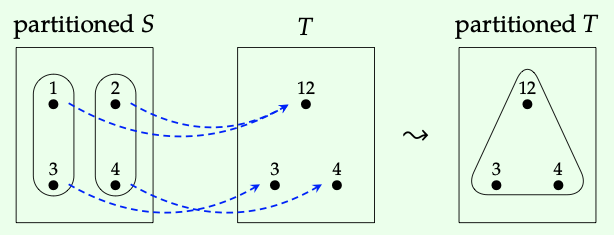
$Screen Shot 2021-01-07 at 8.32.35 PM.png$

Ejercicio 1.103.

Hay 15 particiones diferentes de un conjunto con cuatro elementos. Elige 6 diferentes y para cada uno, llámalo c: S —” P, ¡encuentra g! c), donde S, T,

y g: S → T son los mismos que fueron en el Ejemplo 1.102. ♦

Ejemplo 1.104.

Sea S, T como abajo, y deje que g: S → T sea la función que se muestra en azul. Aquí hay una imagen de cómo$g^{∗}$ toma una partición en T y “la tira hacia atrás” a una partición en S:

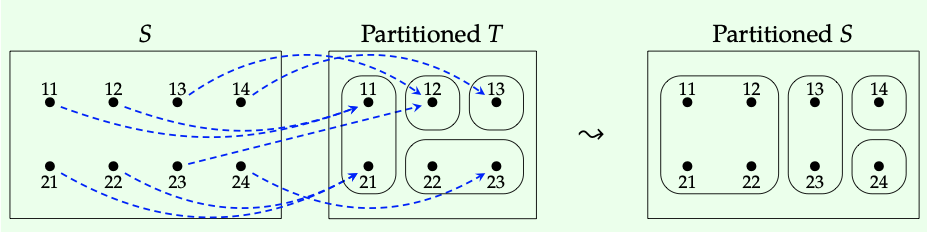
$Screen Shot 2021-01-07 a las 8.38.25 PM.png$

Ejercicio 1.105.

Hay cinco particiones posibles en un conjunto con tres elementos, digamos T = {12,3,4}. Usando las mismas S y g: S → T que en el Ejemplo 1.102, determinar la partición$g^{∗}$ (c) en S para cada una de las cinco particiones c: T - -” P. ♦

Para comprobar que para cualquier función g: S → T, el mapa monótono$g_{!}$: Prt (S) → Prt (T) realmente se deja unido a$g^{∗}$: Prt (T) → Prt (S) tardaría demasiado tiempo para este boceto. Pero el siguiente ejercicio da algunas pruebas.

Ejercicio 1.106.

Sea S, T y g: S → T como en el Ejemplo 1.102.

Elija una partición no trivial c: S —” P y deje que$g_{!}$ (c) sea su partición push forward en T.
Elija cualquier partición más basta d: T —” P ′, es decir, donde$g_{!}$ (c) ≤ d.
Elija cualquier partición no más basta e: T —” Q, es decir, donde$g_{!}$ (c)$\nleq$ e. (Si no puede hacer esto, revise su respuesta para #1.)
Buscar$g^{∗}$ (d) y$g^{∗}$ (e).
La fórmula de amonestación Eq. (1.96) en este caso dice que dado que$g_{!}$ (c) ≤ d y$g_{!}$ (c)$\nleq$ e, deberíamos tener c ≤$g^{∗}$ (d) y c$\nleq$$g^{∗}$ (e). Demuestre que esto es cierto. ♦

Teoría básica de las conexiones Galois

Proposición 1.107

Supongamos que f: P → Q y g: Q → P son mapas monótonos. Los siguientes son equivalentes

f y g forman una conexión Galois donde f se deja junto a g,

(b) por cada $\in$p P y $\in$q Q tenemos

p ≤ g (f (p)) y f (g (q)) ≤ q. (1.108)

Prueba. Supongamos que f se deja junto a g. Tome cualquier p$\in$ P, y deje q: = f (p). Por reflexividad, tenemos f (p) ≤ q, así que por la Definición 1.95 de conexión Galois tenemos p ≤ g (q), pero esto significa p ≤ g (f (p)). La prueba de que f (g (q)) ≤ q es similar.

Ahora supongamos que la Ec. (1.108) mantiene para todos p ∈ P y q ∈ Q. Queremos mostrar que f (p) ≤ q iff p ≤ g (q). Supongamos f (p) ≤ q; entonces dado que g es monótona, g (f (p)) ≤ g (q), pero p ≤ g (f (p)) así que p ≤ g ( q). La prueba de que p ≤ g (q) implica f (p) ≤ q es similar. □

Ejercicio 1.109.

Completa la prueba de la Proposición 1.107 demostrando que

si f se deja unido a g entonces para cualquier q$\in$ Q, tenemos f (g (q)) ≤ q, y
si la Eq. (1.108) se mantiene, entonces mantiene p ≤ g (q) iff f (p) ≤ q mantiene, para todos p$\in$ P y q$\in$ Q. ♦

Si reemplazamos ≤ por = en la Ec. (1.108), recuperamos la definición de isomorfismo (Definición 1.75); es por ello que dijimos al inicio de la Sección 1.4.1 que las conexiones Galois son una especie de versión relajada de los isomorfismos.

Ejercicio 1.110.

Demostrar que si f: P → Q tiene un derecho adjunto g, entonces es único hasta el isomorfismo. Eso significa, para cualquier otro derecho adjunto g ′, tenemos g (q)$\cong$ g ′ (q) para todos q$\in$ Q.
¿Es lo mismo cierto para los colindantes izquierdos? Es decir, si h: P → Q tiene un lado izquierdo, ¿es necesariamente único hasta el isomorfismo? ♦

Proposición 1.111 (Los anexos derechos conservan cumple).

Dejar f: P → Q junto a g: Q → P. Supongamos A$\subseteq$ Q cualquier subconjunto, y deja que g (A) := {g (a) | a $\in$A} sea su imagen. Entonces si A tiene un encuentro$\bigwedge$ A$\in$ Q entonces g (A) tiene un encuentro$\bigwedge$ g (A) en P, y tenemos

g ($\bigwedge A)$$\cong$$\bigwedge$g (A).

Es decir, los anexos derechos preservan se reúne. Del mismo modo, los anexos izquierdos conservan uniones: si A$\subseteq$ P es cualquier subconjunto que tenga una unión V A $\in$P, entonces f (A) tiene una unión V f (A) en Q, y tenemos

f (V A)$\cong$ V f (A).

Prueba. Que f: P → Q y g: Q → P sean mapas monótonos adjuntos, con g derecho contiguo a f. Deje que A$\subseteq$ Q sea cualquier subconjunto y deje que m :=$bigwedge$ A sea su encuentro. Entonces ya que g es monótona g (m) ≤ g (a) para todos a $\in$A, entonces g (m) es un límite inferior para el conjunto g (A). Estaremos hechos si podemos mostrar que g (m) es un mayor límite inferior. Así que toma cualquier otro límite inferior b para g (A); es decir, supongamos que para todos a $\in$A, tenemos b ≤ g (a) y queremos mostrar b ≤ g (m). Entonces por definición de g siendo un derecho adjunto (Definición 1.95), también tenemos f (b) ≤ a. Esto significa que f (b) es un límite inferior para A en Q. Dado que el encuentro m es el mayor límite inferior, tenemos f (b) ≤ m. Una vez más utilizando la conexión Galois, b ≤ g (m), demostrando que g (m) es efectivamente el mayor límite inferior para g (A), según se desee.

El segundo reclamo se prueba de manera similar; ver Ejercicio 1.112.

Ejercicio 1.112.

Completa la prueba de la Proposición 1.111 mostrando que los anexos izquierdos conservan uniones. ♦

Dado que los colindantes izquierdos conservan uniones, sabemos que no pueden tener efectos generativos. De hecho, veremos en el Teorema 1.115 que un mapa monótono no tiene efectos generativos —es decir, conserva los dientes— si y sólo si es una izquierda colindante a algún otro monótono.

Ejemplo 1.113.

Los anexos derechos no necesitan preservar las uniones. Aquí hay un ejemplo:

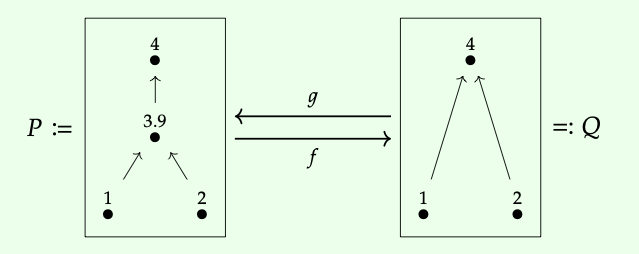
$Screen Shot 2021-01-07 a las 9.06.14 PM.png$

Que g sea el mapa que conserva las etiquetas, y que f sea el mapa que conserva las etiquetas en la medida de lo posible pero con f (3.9) := 4. Ambos son monótonos f y g, y se puede comprobar que g está justo junto a f (ver Ejercicio 1.114). Pero g no conserva uniones porque 1$\lor$ 2 = 4 se mantiene en Q, mientras que g (1)$\lor$ g (2) = 1$\lor$ 2 = 3.9$\neq$ 4 = g (4) en P.

Ejercicio 1.114.

Para estar seguros de que g realmente está justo unido a f en el Ejemplo 1.113, hay doce cosas diminutas que verificar; hazlo. Es decir, por cada p$\in$ P y q$\in$ Q, verificar que f (p) ≤ q iff p ≤ g (q) . ♦

Teorema 1.115 (Teorma de functor adjunto para preordenes).

Supongamos que Q es una preorden que tiene todas las cumple y deja que P sea cualquier preorden. Un mapa monótono g: Q → P conserva cumple si y sólo si es un derecho adjunto.

Del mismo modo, si P tiene todas las uniones y Q es cualquier preorden, un mapa monótono f: P → Q conserva las uniones si y solo si es un adjunto izquierdo.

Comprobante. Solo probaremos el reclamo sobre cumple; el reclamo sobre uniones sigue de manera similar. Demostramos una dirección en la Proposición 1.111, a saber, que los anexos de derecho preservan cumple. Para el otro, supongamos que g es un mapa monótono que conserva las juntas; construiremos una f colindante izquierda.

Definimos a nuestro candidato f: P → Q en cualquier p$\in$ P por

f (p) :=$\bigwedge$ {q$\in$ Q | p$\leq$ g (q)}; (1.116)

este encuentro está bien definido porque Q tiene todas las reuniones, pero para que f sea realmente candidato, necesitamos demostrar que es monótona. Entonces supongamos que p ≤ p ′. Entonces {q ′$\in$ Q | p ′ ≤ g (q ′)}$\subseteq$ {q$\in$ Q | p ≤ g (q)}. Por la Proposición 1.91, esto implica f (p) ≤ f (p ′). Así f es monótona.

Por la Proposición 1.111, basta con mostrar que$p_{0}$ ≤ g (f ($p_{0}$)) y que f (g ($q_{0}$)) ≤$q_{0}$ para todos$p_{0}$$\in$ P y$q_{0}$$\in$ Q. Para el primero, tenemos

$p_{0}$$\leq$$\bigwedge${g (q)$\in$ P |$p_{0}$$\leq$ g (q)}$\cong$ g ($\bigwedge${q$\in$ Q |$p_{0}$$\leq$ g (q)}) = g (f ($p_{0}$),

donde la primera desigualdad se deriva del hecho de que si$p_{0}$ está por debajo de cada elemento de un conjunto, entonces está por debajo de su encuentro, y el isomorfismo es por definición de g conservando cumple. Para el segundo, tenemos

f (g ($q_{0}$) =$\bigwedge$ {q$\in$ Q | g ($q_{0}$)$\leq$ g (q)}$\leq$$\bigwedge$ {$q_{0}$} =$q_{0}$,

donde la primera desigualdad se desprende de la Proposición 1.91 ya que$\subseteq$ {$q_{0}$} {$\in$q Q | g ($q_{0}$) ≤ g (q)}, y el hecho de que$\bigwedge$ {$q_{0}$} =$q_{0}$. □

Ejemplo 1.117.

Sea f: A → B una función entre conjuntos. Podemos imaginar A como un conjunto de manzanas, B como un juego de cubos, y f como poner cada manzana en un cubo.

Entonces tenemos el mapa monótono$f^{∗}$: P (Y) → P (X) que los teóricos de la categoría llaman “retroceso a lo largo de f”. Este mapa lleva un subconjunto B ′$\subseteq$ B a su preimagen$f^{ −1}$ (B ′)$\subseteq$ A: es decir, toma una colección B′ de cubos, y te dice todas las manzanas que contienen en total. Esta operación es monótona (más cubos significa más manzanas) y tiene un lado izquierdo y otro derecho colindantes. El colindante izquierdo$f_{!}$ (A) viene dado por la imagen directa: mapea un subconjunto A ′$\subseteq$ A a

$f_{!}$(A') := {b$\in$ B | existe un$\in$ A' tal que f (a) = b}

Este mapa toma un conjunto A ′ de manzanas, y te dice todos los cubos que contienen al menos una de esas manzanas.

El derecho adjunto$f^{∗}$ mapea un subconjunto A ′$\subseteq$ A a

$f_{*}$(A') := {$\in$b B | para todos a tal que f (a) = b, tenemos un$\in$ A'}

Este mapa toma un conjunto A ′ de manzanas, y te dice todos los cubos b que son todos A ′: todas las manzanas en b son del subconjunto elegido A′. Tenga en cuenta que si un cubo no contiene manzanas en absoluto, entonces a la aspiradora todas sus manzanas son de A ′, por lo que los cubos vacíos cuentan en lo que a lo$f_{∗}$ que respecta.

Observe que las tres operaciones resultan interesantes: comenzar con un conjunto B ′ de cubos y devolver todas las manzanas en ellos, o comenzar con un conjunto A ′ de manzanas y o bien encontrar los cubos que contienen al menos una manzana de A′, o los cubos cuyas únicas manzanas son de A ′. Pero no inventamos estos mapeos$f_{∗}$,$f_{!}$, y$f_{∗}$: fueron inducidos por la función f. Eran automáticos. Es uno de los placeres de la teoría de categorías que tan a menudo los anexos resultan tener interesantes interpretaciones semánticas.

Ejercicio 1.118.

Elija conjuntos X e Y con entre dos y cuatro elementos cada uno, y elija una función f: X → Y.

Elija dos subconjuntos diferentes B 1, B 2$\subseteq$ Y y busque$f^{∗}$ (B1) y$f^{∗}$ (B2).
Elija dos subconjuntos diferentes A 1, A 2$\subseteq$ X y busque$f_{!}$ (A 1) y$f_{!}$ (A 2).
Con los mismos A 1, A 2$\subseteq$ X, encontrar$f_{∗}$ (A 1) y$f_{∗}$ (A 2) . ♦

Operadores de cierre

Dada una conexión Galois con f: P → Q izquierda unida a g: Q → P, podemos componer f y g para llegar a un monotonemap f: P → P de preorden P a sí mismo. Este mapa monótono tiene la propiedad de que p ≤ (f; g) (p), y que (f; g; f; g) (p)$\cong$ (f; g) (p) para cualquier $\in$p P. Este es un ejemplo de un operador de cierre.

Ejercicio 1.119.

Supongamos que f se deja colindante a g. Utilice la Proposición 1.107 para mostrar lo siguiente.

p ≤ (f; g) (p).
(f; g; f; g) (p)$\cong$ (f; g) (p). Para demostrarlo, mostrar desigualdades en ambas direcciones, ≤ y ≥ . ♦

Definición: 1.120.

Un operador de cierre j: P → P en un preorden P es un mapa monótono tal que para todos los $\in$p P tenemos

(a) p ≤ j (p);
(b) j (j (p))$\cong$ j (p).

Ejemplo 1.121.

Aquí un ejemplo de operadores de cierre a partir de cómputos, presentados de manera muy aproximada. Imagine el cálculo como un proceso de reescritura de expresiones de entrada a expresiones de salida. Por ejemplo, una computadora puede reescribir la expresión 7+2+3 como la expresión 12. El conjunto de expresiones aritméticas tiene un orden parcial según si una expresión puede ser reescrita como otra.

Podríamos pensar en un programa de computadora, entonces, como un método para tomar una expresión y reducirla a otra expresión. Entonces es un mapa j: exp → exp. Además, es deseable requerir que este programa de computadora sea un operador de cierre. Monotonicidad significa que si una expresión x se puede reescribir en la expresión y, entonces la reducción j (x) se puede reescribir en j (y). Además, el requisito x ≤ j (x) implica que j sólo puede convertir una expresión en otra si hacerlo es una reescritura permisible. El requisito

j (j (x)) = j (x) implica que si intentas reducir una expresión que ya se ha reducido, el programa de computadora la deja tal cual. Estas propiedades proporcionan una estructura útil en el análisis de la semántica de programas.

Ejemplo 1.122 (Adjunctipms de operadores de cierre).

Así como cada amonestación da lugar a un operador de cierre, a partir de cada operador de cierre podemos construir un adjunction.

Deje que P sea un preorden y deje que j: P → P sea un operador de cierre. Podemos definir un preorden$fix_{j}$ para tener elementos los puntos fijos de j; es decir,

$fix_{j}$:= {p$\in$ P | j (p)$\cong$ p}.

Este es un subconjunto de P, y hereda un orden como resultado; por lo tanto,$fix_{j}$ es un suborden de P. Obsérvese que j (p) es un punto fijo para todos los $\in$p P, ya que j (j (p))$\cong$ j (p).

Definimos un adjunto con el adjunto izquierdo j: P →$fix_{j}$ enviando p a j (p), y derecho adjunto g:$fix_{j}$ → P simplemente la inclusión del subpreorden. Para ver que es realmente una amonestación, necesitamos ver que para cualquier p$\in$ P y q$\in$$fix_{j}$, tenemos j (p) ≤ q si y solo si p ≤ q. Vamos a comprobarlo. Desde p ≤ j (p), tenemos que j (p) ≤ q implica p ≤ q por transitividad. Por el contrario, dado que q es un punto fijo, p ≤ q implica j (p) ≤ j (q)$\cong$ q.

Ejemplo 1.123.

Otro ejemplo de operadores de cierre viene de la lógica. Esto se discutirá en el capítulo final del libro, en particular la Sección 7.4.5, pero aquí daremos una breve descripción general. En esencia, la lógica es el estudio de cuándo una declaración o proposición formal implica otra. Por ejemplo, si n es primo entonces n no es un múltiplo de 6, o si está lloviendo entonces el suelo se está mojando más. Aquí “n es primo”, “n no es múltiplo de 6”, “está lloviendo”, y “el suelo se está mojando” son proposiciones, y dimos dos implicaciones. Toma el conjunto de todas las proposiciones, y ordenarlas por p ≤ q iff p implica q, denotado p ⇒ q. Ya que p ⇒ p y ya que siempre que p ⇒ q y q ⇒ r, también tenemos p ⇒ r, esto es efectivamente un preorder.

Un operador de cierre en él a menudo se llama operador modal. Es una función j de proposiciones a proposiciones, para lo cual p ⇒ j (p) y j (j (p)) = j (p). Un ejemplo de una j es “asumiendo que Bob está en San Diego...” Piense en esto como una proposición B; entonces “asumiendo que Bob está en San Diego, p” significa B ⇒ p. Veamos por qué B ⇒ − es un operador de cierre. Si 'p' es verdad entonces “asumiendo que Bob está en San Diego, p” sigue siendo cierto. Supongamos que “asumiendo que Bob está en San Diego es el caso que, asumiendo que Bob está en San Diego, p 'es cierto”. De ello se deduce que “asumiendo que Bob está en San Diego, p” es cierto. Entonces hemos visto, al menos informalmente, que “suponiendo que Bob esté en San Diego...” es un operador de cierre.

Cambio de nivel

Lo último que queremos discutir en este capítulo es un fenómeno que ocurre a menudo en la teoría de categorías, algo que podríamos llamar informalmente “cambio de nivel”. Es más fácil dar un ejemplo de esto que explicarlo directamente.

Dado cualquier conjunto S, hay un conjunto Rel (S) de relaciones binarias en S. Un elemento R$\in$ Rel (S) es formalmente un subconjunto R$\subseteq$ S × S. Al conjunto Rel (S) se le puede dar un orden a través de la relación de subconjunto, R$\subseteq$ R ′, es decir, si siempre que R ($_{s1}$,$_{s2}$) se mantiene entonces también lo hace R ′ ($_{s1}$,$_{s2}$).

Por ejemplo, el diagrama de Hasse para Rel ({1}) es:

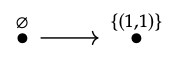
$Screen Shot 2021-01-05 at 3.44.55 PM.png$

Ejercicio 1.124.

Dibuja el diagrama de Hasse para el preorden Rel ({1, 2}) de todas las relaciones binarias en el conjunto {1, 2} . ♦

Para cualquier conjunto S, también hay un conjunto Pos (S), que consiste en todas las relaciones de preorden en S. De hecho hay una estructura de preorden$\sqsubseteq$ en Pos (S), nuevamente dada por inclusión: ≤ está por debajo de ≤′ (escribiremos ≤$\sqsubseteq$ ≤′) si a ≤ b implica a ≤′ b por cada a, b$\in$ S . ¿Un preorden de estructuras de preorden? Eso es lo que queremos decir con un cambio de nivel.

Toda relación de preorden es en particular una relación, por lo que tenemos una inclusión Pos (S) → Rel (S). Este es el derecho colindante de una conexión Galois.

Su lado izquierdo es un mapa monótono Cl: Rel (S) → Pos (S) dado tomando cualquier relación R, escribiéndola en notación infija usando ≤, y tomando el cierre reflexivo y transitivo, es decir, agregando s ≤ s por cada s y añadiendo s ≤ u siempre que s ≤ t y t ≤ u.

Ejercicio 1.125.

Vamos S = {1, 2, 3}. Tratemos de entender el exhorto discutido anteriormente.

1. Cree cualquier relación de preorden ≤ en S, y defina U (≤) para que sea el subconjunto U (≤) := {(s 1, s 2) | s 1 ≤ s 2} S ×$\subseteq$ S, es decir, U (≤) es la imagen de ≤ debajo de la inclusión Pos (S) → Rel (S), la relación 'subyacente' al preorden.

2. Llegar a dos relaciones binarias cualesquiera Q$\subseteq$ S × S y Q ′$\subseteq$ S × S tal que Q$\subseteq$ U (≤) pero Q ′$\nsubseteq$ U (≤). Tenga en cuenta que su elección de Q, Q ′ no tiene que provenir de preordenes.

Ahora queremos comprobar que en este caso, la operación de cierre Cl se deja realmente unida al mapa de 'relación subyacente' U.

3. Concretamente (sin utilizar la aseveración de que existe algún tipo de amonestación), mostrar que Cl (Q)$\sqsubseteq$ ≤, donde$\sqsubseteq$ está el orden en Pos (S), definido inmediatamente por encima de este ejercicio.

4. Concretamente mostrar que Cl (Q ′)$\not\sqsubseteq$ ≤ . ♦