2.4: Multiplicación y División de Enteros
- Page ID
- 113443
Antes de comenzar, que se sepa que los enteros satisfacen las mismas propiedades de multiplicación que los números enteros.
Propiedades de número entero de la multiplicación
Propiedad Conmutativa. Si a y b son números enteros, entonces su producto conmuta. Es decir,
\[a \cdot b = b \cdot a.\nonumber \]
Propiedad Asociativa. Si a, b y c son números enteros, entonces su producto es asociativo. Es decir,
\[(a \cdot b) \cdot c = a \cdot (b \cdot c).\nonumber \]
Identidad Multiplicativa Propiedad. Si a es cualquier número entero, entonces
\[a \cdot 1 = a \text{ and } 1 \cdot a = a.\nonumber \]
Debido a que multiplicar cualquier entero por 1 devuelve el entero idéntico, el entero 1 se llama la identidad multiplicativa.
En la Sección 1.3 aprendimos que la multiplicación equivale a la adición repetida. Por ejemplo,
\[ 3 \cdot 4 = \underbrace{4 + 4 + 4}_{\text{three fours}} \nonumber \]
En la recta numérica, tres juegos de cuatro equivale a caminar tres conjuntos de cuatro unidades a la derecha, comenzando desde cero, como se muestra en la Figura\(\PageIndex{1}\).

Este ejemplo y un poco de pensamiento deberían convencer a los lectores de que el producto de dos enteros positivos siempre será un entero positivo.
El Producto de Dos Enteros Positivos
Si a y b son dos números enteros positivos, entonces su producto ab también es un número entero positivo.
Por ejemplo, 2 · 3 = 6 y 13 · 117 = 1521. En cada caso, el producto de dos enteros positivos es un entero positivo.
El producto de un entero positivo y un entero negativo
Si seguimos con la idea de que la multiplicación equivale a la suma repetida, entonces debe ser que
\[ 3 \cdot (-4) = \underbrace{-4+(-4)+(-4)}_{ \text{three negative fours}}. \nonumber\nonumber \]
Representado en la recta numérica, 3 · (−4) equivaldría entonces a caminar tres series de cuatro unidades negativas (hacia la izquierda), comenzando desde cero, como se muestra en la Figura\(\PageIndex{2}\).
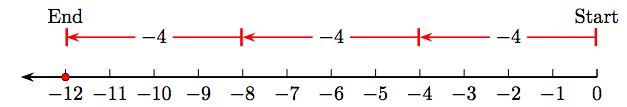
Obsérvese, al menos en este caso particular, que el producto de un entero positivo y un entero negativo es un entero negativo.
Hemos demostrado que 3 · (−4) = −12. Sin embargo, la multiplicación entera es conmutativa, por lo que también debe ser cierto que −4 · 3 = −12. Es decir, el producto de un entero negativo y un entero positivo también es un entero negativo. Aunque no es una prueba, este argumento motiva el siguiente hecho sobre la multiplicación de enteros.
El producto de un entero positivo y un entero negativo
Dos hechos son ciertos:
- Si a es un número entero positivo y b es un número entero negativo, entonces el producto ab es un número entero negativo.
- Si a es un número entero negativo y b es un número entero positivo, entonces el producto ab es un número entero negativo.
Así, por ejemplo, 5 · (−12) = −60 y −13 · 2 = −26. En cada caso la respuesta es negativa porque estamos tomando un producto donde uno de los factores es positivo y el otro es negativo.
La propiedad distributiva
Los enteros satisfacen la propiedad distributiva.
La propiedad distributiva
Que a, b y c sean números enteros. Entonces,
\[a \cdot (b + c) = a \cdot b + a \cdot c.\nonumber \]
Decimos que “la multiplicación es distributiva con respecto a la suma”.
Observe cómo se “distribuye” la a. La a se multiplica por cada término entre paréntesis.
Por ejemplo, considere la expresión 3 · (4 + 5). Podemos evaluar esta expresión según el orden de las operaciones, simplificando primero la expresión dentro de los paréntesis.
\[ \begin{align*} 3 \cdot (4 + 5) &= 3 \cdot 9 \\[4pt] &= 27 \end{align*}\nonumber \]
Pero también podemos usar la propiedad distributiva, multiplicando cada término dentro de los paréntesis por tres, luego simplificando el resultado.
\ [\ begin {aligned} ~ &\ textcolor {rojo} {\ text {Distribuye el 3:}} 3 (4+5)\\
~ &\ textcolor {rojo} {\ text {Realiza multiplicaciones primero:}} = 3\ cdot 4 + 3\ cdot 5\
~ &\ textcolor {rojo} {\ text {Añadir:}} =12+15\
~ &\ textcolor {rojo} {} {\ text {Suma:}} =27 \\
\ final {alineado}\ nonumber\]
Tenga en cuenta que evaluar 3 · (4 + 5) usando la propiedad distributiva proporciona el mismo resultado que la evaluación (2.1) usando el orden de las operaciones.
La propiedad multiplicativa del cero
La propiedad distributiva se puede utilizar para proporcionar pruebas de una serie de propiedades importantes de números enteros. Una propiedad importante es el hecho de que si multiplicas un entero por cero, el producto es cero. Aquí hay una prueba de ese hecho que utiliza la propiedad distributiva.
Dejar a ser cualquier entero. Entonces,
\[ \begin{aligned} a \cdot 0 = a \cdot (0 + 0) ~ & \textcolor{red}{ \text{ Additive Identity Property: = 0 + 0 = 0.}} \\ a \cdot 0 = a \cdot 0 + a \cdot 0 ~ & \textcolor{red}{ \text{ Distribute } a \text{ times each zero in the parentheses.}} \end{aligned}\nonumber \]
A continuación, para “deshacer” el efecto de sumar un · 0, restar a · 0 de ambos lados de la ecuación.
\[ \begin{aligned} a \cdot 0 - a \cdot 0 = a \cdot 0 + a \cdot 0 + a \cdot 0 - a \cdot 0 ~ & \textcolor{red}{ \text{ Subtract } a \cdot 0 \text{ from both sides.}} \\ 0 = a \cdot 0 ~ & \textcolor{red}{ a \cdot 0 - a \cdot 0 = 0 \text{ on each side.}} \end{aligned}\nonumber \]
Propiedad Multiplicativa de Cero
Dejar a representar cualquier número entero. Entonces
a · 0 = 0 y 0 · a = 0.
Así, por ejemplo, −18 · 0 = 0 y 0 · 122 = 0.
Multiplicar por Menos Uno
Aquí hay otra aplicación útil de la propiedad distributiva.
\ [\ begin {aligned} (-1) a + a = (-1) a + 1a ~ &\ textcolor {rojo} {\ text {Reemplazar} a\ text {con} 1a.}\\
= (-1 + 1) a ~ &\ textcolor {rojo} {\ text {Usa la propiedad distributiva para descontar} a.} \\
=0a ~ &\ textcolor {rojo} {\ texto {Reemplazar} -1+1\ texto {con} 0.} \\
=0~ &\ textcolor {rojo} {\ texto {Reemplazar} 0a\ texto {con 0.}} \ end {alineado}\ nonumber\]
Así, (−1) a + a = 0. Es decir, si agregas (−1) a a a obtienes cero. Sin embargo, la propiedad inversa aditiva dice que − a es el número único que se agrega a a para obtener cero. La conclusión debe ser que (−1) a = − a.
Multiplicar por Menos Uno
Si a es cualquier número entero, entonces
\[(−1)a = −a.\nonumber \]
Así, por ejemplo, −1 (4) = −4 y −1 (−4) = − (−4) = 4.
Esta propiedad es bastante importante, como veremos en futuros trabajos. No sólo nos dice que (−1) a = − a, sino que también nos dice que si vemos − a, entonces se puede interpretar que significa (−1) a.
El Producto de Dos Enteros Negativos
Podemos emplear la propiedad multiplicativa de −1, es decir, (−1) a = − a para encontrar el producto de dos números negativos.
\[ \begin{aligned} (-4)(-3) = [(-1)(4)](-3) ~ & \textcolor{red}{ \text{ Replace } -4 \text{ with } (-1)(4).} \\ =(-1)[(4)(-3)] ~ & \textcolor{red}{ \text{ Use the associative property to regroup.}} \\ = (-1)(-12) ~ & \textcolor{red}{ \text{ We know: } (4)(-3) = -12.} \\ = -(-12) ~ & \textcolor{red}{ (-1)a = -a. \text{ Here } (-1)(-12) = -(-12).} \\ =12 ~ & \textcolor{red}{ -(-a) = a. \text{ Here } -(-12) = 12.} \end{aligned}\nonumber \]
Así, al menos en el caso de (−4) (−3), el producto de dos enteros negativos es un entero positivo. Esto es cierto en general.
El Producto de Dos Enteros Negativos
Si tanto a como b son números enteros negativos, entonces su producto ab es un número entero positivo.
Así, por ejemplo, (−5) (−7) = 35 y (−112) (−6) = 672. En cada caso la respuesta es positiva, porque el producto de dos enteros negativos es un entero positivo.
Dispositivo de memoria
Aquí hay un dispositivo de memoria simple para ayudar a recordar las reglas para encontrar el producto de dos enteros.
Signos similares y diferentes
Hay dos casos:
A diferencia de Signos. El producto de dos enteros con signos diferentes es negativo. Es decir:
(+) (−) = −
(−) (+) = −
Como Signos. El producto de dos enteros con signos similares es positivo. Es decir:
(+) (+) = +
(−) (−) =+
Ejemplo 1
Simplificar: (a) (−3) (−2), (b) (4) (−10) y (c) (12) (−3).
Solución
En cada ejemplo, utilizamos el enfoque de signos “me gusta” y “diferente”.
a) Los signos similares dan un resultado positivo. Por lo tanto, (−3) (−2) = 6.
b) A diferencia de los signos da un resultado negativo. Por lo tanto, (4) (−10) = −40.
c) A diferencia de los signos da un resultado negativo. Por lo tanto, (12) (−3) = −36.
Ejercicio
Simplificar: (a) (−12) (4) y (b) (−3) (−11).
- Contestar
-
(a) −48, (b) 33
Ejemplo 2
Simplifique (−3) (2) (−4) (−2).
Solución
El orden de operaciones exige que trabajemos de izquierda a derecha.
\[ \begin{aligned} (-3)(2)(-4)(-2) = (-6)(-4)(-2) ~ & \textcolor{red}{ \text{ Work left to right: } (-3)(2) = -6.} \\ = (24)(-2) ~ & \textcolor{red}{ \text{ Work left to right: } (-6)(-4) = 24.} \\ =-48 ~ & \textcolor{red}{ \text{ Multiply: } (24)(-2) = -48.} \end{aligned}\nonumber \]
Por lo tanto, (−3) (2) (−4) (−2) = −48.
Ejercicio
Simplificar: (−2) (−3) (4) (−1).
- Contestar
-
−24.
Ejemplo 3
Simplificar: (a) (−2) 3 y (c) (−3) 4.
Solución
En cada ejemplo, use
\[ a^m = \underbrace{a \cdot a \cdot a \cdot \cdots \cdot a}_{m \text{ times}},\nonumber \]
luego trabajar de izquierda a derecha con la multiplicación.
a) Utilizar la definición de exponente, luego orden de operaciones.
\[ \begin{aligned} (-2)^3 = (-2)(-2)(-2) ~ & \textcolor{red}{ \text{ Write } -2 \text{ as a factor three times.}} \\ =4(-2) ~ & \textcolor{red}{ \text{ Work left to right: } (-2)(-2) = 4.} \\ =-8 \end{aligned}\nonumber \]
b) Utilizar la definición de exponente, luego orden de operaciones.
\[ \begin{aligned} (-3)^4 = (-3)(-3)(-3)(-3) ~ & \textcolor{red}{ \text{ Write } -3 \text{ as a factor four times.}} \\ =9(-3)(-3) ~ & \textcolor{red}{ \text{ Work left to right: } (-3)(-3) = 9.} \\ =-27(-3) ~ & \textcolor{red}{ \text{ Work left to right: } 9(-3) = -27.} \\ = 81 \end{aligned}\nonumber \]
Ejercicio
Simplificar: (a) (−2) 2 y (b) −2 2.
- Contestar
-
(a) 4 y (b) −4
El ejemplo 3 motiva el siguiente hecho.
Par e impar
Dos hechos son aparentes.
- Si un producto contiene un número impar de factores negativos, entonces el producto es negativo.
- Si un producto contiene un número par de factores negativos, entonces el producto es positivo.
Así, por ejemplo,
\[(−2)^5 = (−2)(−2)(−2)(−2)(−2) = −32\nonumber \]
evalúa rápidamente como −32 ya que tiene un número impar de factores negativos. Por otra parte,
\[(−2)^6 = (−2)(−2)(−2)(−2)(−2)(−2) = 64\nonumber \]
rápidamente evalúa como 64 ya que tiene un número par de factores negativos.
División de Enteros
Considera que
\(\frac{12}{3} = 4\)porque\(3(4) = 12\) y\(\frac{-12}{-3} = 4\) porque\(-3(4) = -12\).
De la misma manera,
\(\frac{12}{-3} = -4\)porque -3 (-4) = 12 y\(\frac{-12}{3} = -4\) porque\(3(-4) = -12\).
Así, las reglas para dividir enteros son las mismas que las reglas para multiplicar enteros.
Signos similares y diferentes
Hay dos casos:
A diferencia de Signos. El cociente de dos enteros con signos diferentes es negativo. Es decir,
\[ \begin{array} \frac{(+)}{(-)} = - \\ \frac{(-)}{(+)} = - \end{array}\nonumber \]
Como Signos. El cociente de dos enteros con signos similares es positivo. Es decir,
\[ \begin{array} \frac{(+)}{(+)} = + \\ \frac{(-)}{(-)} = + \end{array}\nonumber \]
Así, por ejemplo, 12/ (−6) = −2 y −44/ (−4) = 11. En el primer caso, a diferencia de los signos da un cociente negativo. En el segundo caso, como signos da un cociente positivo.
Un último recordatorio.
División por Cero no está definida
Si a es cualquier entero, el cociente
\[ \frac{a}{0}\nonumber \]
está indefinido. La división por cero no tiene sentido.
Consulte la discusión en la Sección 1.3 para una discusión sobre la división por cero.
Ejemplo 4
Simplifique: (a) −12/ (−4), (b) 6/ (−3) y (c) −15/0.
Solución
En cada ejemplo, utilizamos el enfoque de signos “me gusta” y “diferente”.
a) Los signos similares dan un resultado positivo. De ahí que,
\[ \frac{-12}{-4} = 3.\nonumber \]
b) A diferencia de los signos da un resultado negativo. De ahí que,
\[ \frac{6}{-3} = -2.\nonumber \]
c) La división por cero no está definida. De ahí que,
\[ \frac{-15}{0}\nonumber \]
está indefinido.
Ejercicio
Simplificar: (a) −24/4 y (b) −28/ (−7).
- Contestar
-
(a) −6, (b) 4
Ejercicios
En los Ejercicios 1-16, declarar la propiedad de multiplicación representada por la identidad dada.
1. (−2) (−16) (13) = (−2) (−16) (13)
2. (10) (−15) (−6) = (10) (−15) (−6)
3. (−17) (−10) = (−10) (−17)
4. (−5) (3) = (3) (−5)
5. (4) (11) = (11) (4)
6. (−5) (−11) = (−11) (−5)
7. 16 · (8 + (−15) = 16 · 8 + 16 · (−15)
8. 1 · (−16 + (−6) = 1 · (−16) + 1 · (−6)
9. (17) (20) (11) = (17) (20) (11)
10. (14) (−20) (−18) = (14) (−20) (−18)
11. −19 · 1 = −19
12. −17 · 1 = −17
13. 8 · 1=8
14. −20 · 1 = −20
15. 14 · (−12 + 7 = 14 · (−12) + 14 · 7
16. −14 · (−3+6 = −14 · (−3) + (−14) · 6
En los Ejercicios 17-36, simplifique cada expresión dada.
17. 4 · 7
18. 4 · 2
19. 3 · (−3)
20. 7 · (−9)
21. −1 · 10
22. −1 · 11
23. −1 · 0
24. −8 · 0
25. −1 · (−14)
26. −1 · (−13)
27. −1 · (−19)
28. −1 · (−17)
29. 2 · 0
30. −6 · 0
31. −3 · 8
32. 7 · (−3)
33. 7 · 9
34. 6 · 3
35. −1 · 5
36. −1 · 2
En los Ejercicios 37-48, simplificar cada expresión dada.
37. (−7) (−1) (3)
38. (10) (6) (3)
39. (−7) (9) (10) (−10)
40. (−8) (−5) (7) (−9)
41. (6) (5) (8)
42. (7) (−1) (−9)
43. (−10) (4) (−3) (8)
44. (8) (−2) (−5) (2)
45. (6) (−3) (−8)
46. (−5) (−4) (1)
47. (2) (1) (3) (4)
48. (7) (5) (1) (4)
En Ejercicios 49-60, computa el valor exacto.
49. (−4) 4
50. (−3) 4
51. (−5) 4
52. (−2) 2
53. (−5) 2
54. (−3) 3
55. (−6) 2
56. (−6) 4
57. (−4) 5
58. (−4) 2
59. (−5) 3
60. (−3) 2
En los Ejercicios 61-84, simplificar cada expresión dada.
61. −16 ÷ (−8)
62. −33 ÷ (−3)
63. \( \frac{-8}{1}\)
64. \(\frac{40}{-20}\)
65. \(\frac{-1}{0}\)
66. \ (\ frac {2} {0}\
67. −3 ÷ 3
68. −58 ÷ 29
69. \(\frac{56}{-28}\)
70. \(\frac{60}{-12}\)
71. 0 ÷ 15
72. 0 ÷ (−4)
73. \(\frac{63}{21}\)
74. \(\frac{-6}{-1}\)
75. \(\frac{78}{13}\)
76. \(\frac{-84}{-14}\)
77. 0 ÷ 5
78. 0 ÷ (−16)
79. \(\frac{17}{0}\)
80. \(\frac{-20}{0}\)
81. −45 ÷ 15
82. −28 ÷ 28
83. 12 ÷ 3
84. −22 ÷ (−22)
85. Buceo. Un buzo baja 25 pies. Luego, un segundo buceador se sumerge 5 veces más que el primer buceador. Escribe la profundidad final del segundo buceador como un entero.
86. Pérdida de inversión. Un club inversionista de cinco amigos ha perdido $4400 en una operación. Si comparten la pérdida por igual, escriba la pérdida de cada uno de los miembros como un número entero.
RESPUESTAS
1. Propiedad asociativa de la multiplicación
3. Propiedad conmutativa de la multiplicación
5. Propiedad conmutativa de la multiplicación
7. Propiedad distributiva
9. Propiedad asociativa de la multiplicación
11. Propiedad de identidad multiplicativa
13. Propiedad de identidad multiplicativa
15. Propiedad distributiva
17. 28
19. −9
21. −10
23. 0
25. 14
27. 19
29. 0
31. −24
33. 63
35. −5
37. 21
39. 6300
41. 240
43. 960
45. 144
47. 24
49. 256
51. 625
53. 25
55. 36
57. −1024
59. −125
61. 2
63. −8
65. La división por cero no está definida.
67. −1
69. −2
71. 0
73. 3
75. 6
77. 0
79. La división por cero no está definida.
81. −3 83. 4
85. −125 pies


