2.3: Restar enteros

En la Sección 1.2, afirmamos que “la resta es lo opuesto a la suma”. Así, para restar 4 de 7, caminamos siete unidades a la derecha en la recta numérica, pero luego caminamos 4 unidades en sentido contrario (hacia la izquierda), como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): La resta requiere que invertimos la dirección.

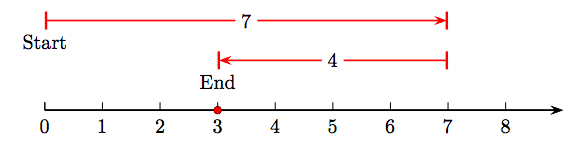
Así, 7 − 4 = 3. La frase clave es “agregar lo contrario”. Así, la resta 7 − 4 se convierte en la suma 7 + (−4), que imaginaríamos en la recta numérica como se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Las medias de sustracción suman lo contrario.

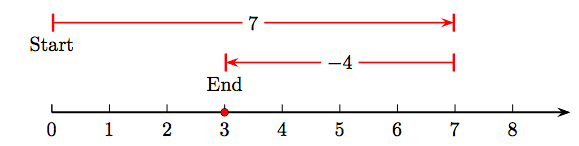
La figura\(\PageIndex{1}\) y la figura\(\PageIndex{2}\) proporcionan una amplia evidencia de que la resta 7−4 es idéntica a la suma 7+ (−4). Nuevamente, resta significa “sumar lo contrario”. Es decir, 7 − 4=7+ (−4).

Definición de la resta

Resta significa “sumar lo contrario”. Es decir, si a y b son números enteros, entonces

\[a − b = a + (−b).\nonumber \]

Así, por ejemplo, −123−150 = −123+ (−150) y −57− (−91) = −57+91. En cada caso, resta significa “sumar lo contrario”. En el primer caso, restar 150 es lo mismo que sumar −150. En el segundo caso, restar−91 es lo mismo que sumar 91.

Ejemplo 1

Encuentra las diferencias: (a) 4 − 8, (b) −15 − 13 y (c) −117 − (−115).

Solución

En cada caso, resta significa “sumar lo contrario”.

a) Cambiar la resta a suma con la frase “resta significa sumar lo contrario”. Es decir, 4−8 = 4+ (−8). Ahora podemos realizar esta adición en la línea numérica.

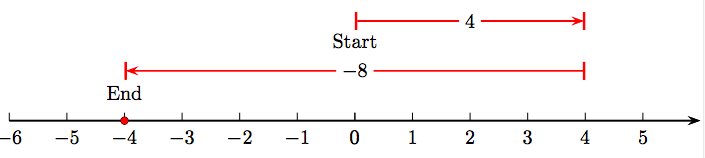
Así, 4 − 8=4+ (−8) = −4.

b) Primero cambie la resta a suma “sumando lo contrario”. Es decir, −15 − 13 = −15 + (−13). Ahora podemos usar la intuición física para realizar la adición. Comienza en el origen (cero), camina 15 unidades a la izquierda, luego 13 unidades adicionales a la izquierda, llegando a la respuesta −28. Es decir,

\[ \begin{aligned} −15 − 13 & = −15 + (−13) \\ ~ & = −28. \end{aligned}\nonumber \]

c) Primero cambie la resta a suma “sumando lo contrario”. Es decir, −117 − (−115) = −117 + 115. Usando “Sumando dos enteros con signos diferentes” de la Sección 2.2, primero resta la magnitud menor de la magnitud mayor; es decir, 117 − 115 = 2. Debido a que −117 tiene la magnitud mayor y su signo es negativo, prefija un signo negativo a la diferencia de magnitudes. Por lo tanto,

\[ \begin{aligned} −117 − (−115) & = −117 + 115 \\ & = −2. \end{aligned}\nonumber \]

Ejercicio

Utilice cada una de las técnicas en las partes (a), (b) y (c) del Ejemplo 1 para evaluar la diferencia −11 − (−9).

Responder

−2

Orden de Operaciones

Ahora aplicaremos el “Orden de Operaciones Rector de Reglas” de la Sección 1.5 a una serie de ejercicios de ejemplo.

Ejemplo 2

Simplificar −5 − (−8) − 7.

Solución

Trabajamos de izquierda a derecha, cambiando cada resta “sumando lo contrario”.

\[ \begin{aligned} -5-(-8) -7=-5+8+(-7) ~ & \textcolor{red}{ \text{ Add the opposite of } -8, \text{ which is 8.}} \\ ~ & \textcolor{red}{ \text{ Add the opposite of 7, which is } -7.} \\ =3 +(-7) & \textcolor{red}{ \text{ Working left to right, } -5+8=3.} \\ =-4 ~ & \textcolor{red}{3 +(-7) = -4.} \end{aligned}\nonumber \]

Ejercicio

Simplificar: −3 − (−9) − 11.

Responder

−5

Los símbolos de agrupación dicen “hazme primero”.

Ejemplo\(\PageIndex{1}\)

Simplificar −2 − (−2 − 4).

Solución

Las expresiones entre paréntesis deben evaluarse primero.

\[ \begin{aligned} -2(-2-4)=-2-(-2+(-4)) ~ & \textcolor{red}{ \text{ Simplify the parenthetical expression}} \\ ~ & \textcolor{red}{ \text{ first. Add the opposite of 4, which is } -4.} \\ = -2 -(-6) ~ & \textcolor{red}{ \text{ Inside the parentheses, } -2 + (-4) = -6.} \\ =-2 + 6 ~ & \textcolor{red}{ \text{ Subtracting a } -6 \text{ is the same as adding a 6.}} \\ =4 ~ & ~ \textcolor{red}{ \text{ Add: } -2 + 6 = 4.} \end{aligned}\nonumber \]

Ejercicio

Simplificar: −3 − (−3 − 3).

Responder

3

El cambio como diferencia

Supongamos que cuando salgo de mi casa a primera hora de la mañana, la temperatura exterior es de 40 ^◦ Fahrenheit. Más tarde en el día, la temperatura mide 60◦ Fahrenheit. ¿Cómo mido el cambio en la temperatura?

El cambio en una cantidad

Para medir el cambio en una cantidad, restar siempre la primera medida de la segunda. Es decir:

\[ \colorbox{cyan}{Change in a Quantity} = \colorbox{cyan}{Latter Measurement} - \colorbox{cyan}{Former Measurement}\nonumber \]

Así, para medir el cambio de temperatura, realizo una resta de la siguiente manera:

\[ \begin{aligned} \colorbox{cyan}{Change in Temperature} & = \colorbox{cyan}{Latter Measurement} & - & \colorbox{cyan}{Former Measurement} \\ ~ & = 60^{ \circ} \text{F} & - & 40^{ \circ} \text{F} \\ ~ & = 20^{ \circ} \text{F} \end{aligned}\nonumber \]

Tenga en cuenta que la respuesta positiva está de acuerdo con el hecho de que la temperatura ha aumentado.

Ejemplo 4

Supongamos que por la tarde, la temperatura mide 65 ^◦ Fahrenheit, luego a última hora de la noche la temperatura desciende a 44 ^◦ Fahrenheit. Encuentra el cambio de temperatura.

Solución

Para medir el cambio de temperatura, debemos restar la primera medida de la segunda.

\[ \begin{aligned} \colorbox{cyan}{Change in Temperature} & = \colorbox{cyan}{Latter Measurement} & - & \colorbox{cyan}{Former Measurement} \\ ~ & = 44^{ \circ} \text{F} & - & 65^{ \circ} \text{F} \\ ~ & = -11^{ \circ} \text{F} \end{aligned}\nonumber \]

Tenga en cuenta que la respuesta negativa está de acuerdo con el hecho de que la temperatura ha disminuido. Ha habido un “cambio” de −11 ^◦ Fahrenheit.

Ejercicio

Marianne despierta a una temperatura matutina de 54 ^◦ Fahrenheit. Golpea una tormenta, bajando la temperatura a 43 ^◦ Fahrenheit. Encuentra el cambio de temperatura.

Responder

−11◦ Fahrenheit

Ejemplo 5

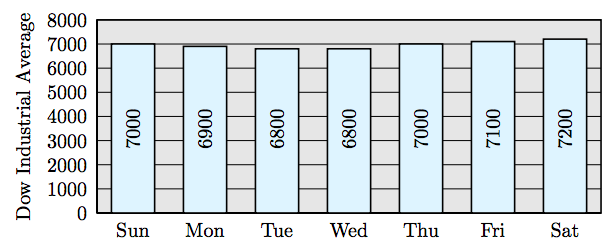
A veces un gráfico de barras no es la visualización más adecuada para tus datos. Por ejemplo, considere el gráfico de barras en la Figura\(\PageIndex{3}\) que representa el Promedio Industrial Dow durante siete días consecutivos en marzo de 2009. Debido a que las barras son de altura casi igual, es difícil detectar fluctuación o cambio en el Promedio Industrial Dow.

Determinemos el cambio en el promedio de Dow Industrial en el día a día. Recuerde restar esta última medida menos la primera (día actual menos día anterior). Esto nos da los siguientes cambios.

Jornadas Consecutivas	Cambio en Promedio Industrial Dow
dom-lun	6900 - 7000 = -100
Lun-martes	6800 - 6900 = -100
Mares-Mié	6800 - 6800 = 0
mié-jue	7000 - 6800 = 200
Jue-Vie	7100 - 7000 = 100
Vie-Sáb	7200 - 7100 = 100

Figura\(\PageIndex{3}\): Gráfico de barras de pérdidas y ganancias.

Utilizaremos los datos de la tabla para construir un gráfico de líneas. En el eje horizontal, colocamos los pares de días consecutivos (ver Figura\(\PageIndex{4}\)). En el eje vertical colocamos el Cambio en el Promedio Dow Industrial. A cada par de días trazamos un punto a una altura igual al cambio en Promedio Industrial Dow calculado en nuestra tabla.

Figura\(\PageIndex{4}\): Gráfico del cambio en Dow frente a días consecutivos.

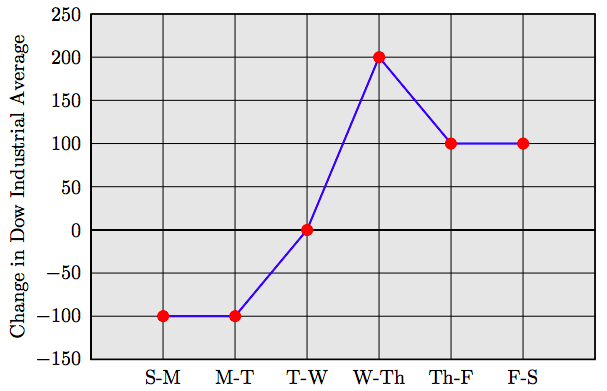
Tenga en cuenta que los datos mostrados por la Figura muestran\(\PageIndex{4}\) más fácilmente los cambios en el Promedio Industrial Dow en el día a día. Por ejemplo, ahora es fácil escoger el día que vio el mayor incremento en el Dow (de miércoles a jueves, el Dow subió 200 puntos).

Ejercicios

En Ejercicios 1-24, encuentra la diferencia.

1. 16 − 20

2. 17 − 2

3. 10 − 12

4. 16 − 8

5. 14 − 11

6. 5 − 8

7. 7 − (−16)

8. 20 − (−10)

9. −4 − (−9)

10. −13 − (−3)

11. 8 − (−3)

12. 14 − (−20)

13. 2 − 11

14. 16 − 2

15. −8 − (−10)

16. −14 − (−2)

17. 13 − (−1)

18. 12 − (−13)

19. −4 − (−2)

20. −6 − (−8)

21. 7 − (−8)

22. 13 − (−14)

23. −3 − (−10)

24. −13 − (−9)

---

En los Ejercicios 25-34, simplificar la expresión dada.

25. 14 − 12 − 2

26. −19 − (−7) − 11

27. −20 − 11 − 18

28. 7 − (−13) − (−1)

29. 5 − (−10) − 20

30. −19 − 12 − (−8)

31. −14 − 12 − 19

32. −15 − 4 − (−6)

33. −11 − (−7) − (−6)

34. 5 − (−5) − (−14)

---

En Ejercicios 35-50, simplificar la expresión dada.

35. −2 − (−6 − (−5))

36. 6 − (−14 − 9)

37. (−5 − (−8)) − (−3 − (−2))

38. (−6 − (−8)) − (−9 − 3)

39. (6 − (−9)) − (3 − (−6))

40. (−2 − (−3)) − (3 − (−6))

41. −1 − (10 − (−9))

42. 7 − (14 − (−8))

43. 3 − (−8 − 17)

44. 1 − (−1 − 4)

45. 13 − (16 − (−1))

46. −7 − (−3 − (−8))

47. (7 − (−8)) − (5 − (−2))

48. (6 − 5) − (7 − 3)

49. (6 − 4) − (−8 − 2)

50. (2 − (−6)) − (−9 − (−3))

---

51. La primera temperatura registrada es de 42 ^◦ F. Cuatro horas después, la segunda temperatura es de 65 ^◦ F. ¿Cuál es el cambio de temperatura?

52. La primera temperatura registrada es de 79 ^◦ F. Cuatro horas después, la segunda temperatura es de 46 ^◦ F. ¿Cuál es el cambio de temperatura?

53. La primera temperatura registrada es de 30 ^◦ F. Cuatro horas después, la segunda temperatura es de 51 ^◦ F. ¿Cuál es el cambio de temperatura?

54. La primera temperatura registrada es de 109 ^◦ F. Cuatro horas después, la segunda temperatura es de 58 ^◦ F. ¿Cuál es el cambio de temperatura?

55. Las temperaturas típicas en Fairbanks, Alaska en enero son −2 grados Fahrenheit durante el día y −19 grados Fahrenheit por la noche. ¿Cuál es el cambio de temperatura del día a la noche?

56. Las temperaturas típicas de verano en Fairbanks, Alaska en julio son de 79 grados Fahrenheit durante el día y 53 grados Fahrenheit por la noche. ¿Cuál es el cambio de temperatura del día a la noche?

57. Comunicación. Un submarino a 1600 pies bajo el nivel del mar se comunica con un piloto que vuela 22,500 pies en el aire directamente sobre el submarino. ¿Hasta dónde va el comunicado?

58. De mayor a menor. El punto más alto de la tierra se encuentra en el Monte Everest en Nepal-Tíbet a 8,848 metros. El punto más bajo de la corteza terrestre es la Fosa de las Marianas en el Océano Pacífico Norte a 10.923 metros bajo el nivel del mar. ¿Cuál es la distancia entre los puntos más altos y los más bajos de la tierra? Wikipedia http://en.Wikipedia.org/wiki/Extremes_on_Earth

59. Elevación más baja. El punto más bajo en América del Norte es Death Valley, California a -282 pies. El punto más bajo de toda la masa terrestre se encuentra en las orillas del Mar Muerto a lo largo de la frontera entre Israel y Jordania con una elevación de -1,371 pies. ¿Cuánto más baja es la orilla del Mar Muerto de Valle de la Muerte?

60. Puntuaciones de exámenes. Las puntuaciones de Freida en sus primeros siete exámenes de matemáticas se muestran en el siguiente gráfico de barras. Calcular las diferencias entre exámenes consecutivos, luego crear una gráfica lineal de las diferencias en cada par de exámenes consecutivos. ¿Entre qué dos pares de exámenes consecutivos mostró Freida la mayor mejora?

---

RESPUESTAS

1. −4

3. −2

5. 3

7. 23

9. 5 11. 11 13. −9 15. 2 17. 14 19. −2 21. 15 23. 7 25. 0 27. −49 29. −5 31. −45 33. 2 35. −1 37. 4 39. 6 41. −20 43. 28 45. −4 47. 8 49. 12 51. 23◦ F 53. 21◦ F 55. −17 grados Fahrenheit 57. 24,100 grados Fahrenheit 57. 24,100 pies 59. 1,089 pies más bajos