3.2: Evaluación de expresiones algebraicas

Última actualización
Guardar como PDF

Page ID: 113406

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En esta sección evaluaremos expresiones algebraicas para valores dados de las variables contenidas en las expresiones. A continuación te presentamos algunos consejos simples para ayudarte a tener éxito.

Consejos para evaluar expresiones algebraicas

Reemplazar todas las ocurrencias de variables en la expresión con paréntesis abiertos. Dejar espacio entre paréntesis para sustituir el valor dado de la variable.
Sustituir los valores dados de las variables en los paréntesis abiertos preparados en el primer paso.
Evaluar la expresión resultante de acuerdo con el Orden de Operaciones Rector de Reglas.

Empecemos con un ejemplo.

Ejemplo 1

Evaluar la expresión$x^2 − 2xy + y^2$ en$x = −3$ y$y = 2$.

Solución

Después de “Consejos para evaluar expresiones algebraicas”, primero reemplace todas las ocurrencias de variables en la expresión x ² − 2 xy + y ² con paréntesis abiertos.

\[ x^2 -2xy + y^2 = ( ~ )^2 -2(~)(~) + ( ~ )^2 \nonumber\nonumber \]

En segundo lugar, sustituir cada variable por su valor dado, y tercero, seguir las “Reglas que guían el orden de operaciones” para evaluar la expresión resultante.

\[ \begin{aligned} x^2 -2xy + y^2 ~ & \textcolor{red}{ \text{ Original expression.}} \\ =( \textcolor{red}{-3} )^2 -2 ( \textcolor{red}{-3})( \textcolor{red}{2}) + (\textcolor{red}{2})^2 ~ & \textcolor{red}{ \text{ Substitute } -3 \text{ for } x \text{and 2 for }y.} \\ =9-2(-3)(2)+4 ~ & \textcolor{red}{ \text{ Evaluate exponents first.}} \\ = 9-(-6)(2)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply } 2(-3)=-6.} \\ =9-(-12)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply: } (-6)(2) = -12.} \\ = 9 + 12 + 4 ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = 25 ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]

Ejercicio

Si x = −2 e y = −1, evalúe x ³ − y ³.

Responder: −7

Ejemplo 2

Evaluar la expresión (a − b) ² Si a = 3 y b = −5, a a = 3 y b = −5.

Solución

Después de “Consejos para evaluar expresiones algebraicas”, primero reemplace todas las ocurrencias de variables en la expresión (a − b) ² con paréntesis abiertos.

\[ (a-b)^2 = (()-())^2\nonumber \]

En segundo lugar, sustituir cada variable por su valor dado, y tercero, seguir las “Reglas que guían el orden de operaciones” para evaluar la expresión resultante.

\[ \begin{aligned} (a-b)^2 = (( \textcolor{red}{3})-( \textcolor{red}{-5}))^2 ~ & \textcolor{red}{ \text{ Substitute 3 for } a \text{ and } -5 \text{ for } b.} \\ = (3+5)^2 ~ & \textcolor{red}{ \text{ Add the opposite: } (3)-(-5)=3+5} \\ = 8^2 ~ & \textcolor{red}{ \text{ Simplify inside parentheses: } 3+5 = 8} \\ =64 ~ & \textcolor{red}{ \text{ Evaluate exponent: } 8^2 = 64} \end{aligned}\nonumber \]

Ejercicio

Si a = 3 y b = −5, evalúe a ² − b ².

Responder: −16

Ejemplo 3

Evalúe la expresión |a|−|b| a = 5 y b = −7.

Solución

Después de “Consejos para evaluar expresiones algebraicas”, primero reemplace todas las ocurrencias de variables en la expresión |a|−|b| con paréntesis abiertos.

\[ |a| - |b| = |( ~ )| - |( ~ )|\nonumber \]

En segundo lugar, sustituir cada variable por su valor dado, y tercero, seguir las “Reglas que guían el orden de operaciones” para evaluar la expresión resultante.

\[ \begin{aligned} |a| - |b| = |( \textcolor{red}{5} )| = |( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = 5 - 7 ~ & \textcolor{red}{ \text{ Absolute values first: } |(5)| = 5 \text{ and } |(-7)|=7|} \\ =5+(-7) ~ & \textcolor{red}{ \text{ Add the opposites: } 5 - 7 = 5+(-7).} \\ =-2 ~ & \textcolor{red}{ \text{ Add: } 5+(-7)=-2.} \end{aligned}\nonumber \]

Ejercicio

Si a = 5 y b = −7, evalúe 2| a | − 3| b |.

Responder: −11

Ejemplo 4

Evaluar la expresión | a − b | a = 5 y b = −7.

Solución

Después de “Consejos para evaluar expresiones algebraicas”, primero reemplace todas las ocurrencias de variables en la expresión | a − b | con paréntesis abiertos.

\[ |a-b| = |(~)-(~)|\nonumber \]

En segundo lugar, sustituir cada variable por su valor dado, y tercero, seguir las “Reglas que guían el orden de operaciones” para evaluar la expresión resultante.

\[ \begin{aligned} |a-b| = |( \textcolor{red}{5})-( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = |5+7| ~ & \textcolor{red}{ \text{ Add the opposite: } 5-(-7)=5+7.} \\ =|12| ~ & \textcolor{red}{ \text{ Add: } 5+7=12.} \\ =12 ~ & \textcolor{red}{ \text{ Take the absolute value: } |12| = 12.} \end{aligned}\nonumber \]

Ejercicio

Si a = 5 y b = −7, evalúe |2 a − 3 b |.

Responder: 31

Ejemplo 5

Evaluar la expresión

\[ \frac{ad-bc}{a+b}\nonumber \]

a = 5, b = −3, c = 2 y d = −4.

Solución

Después de “Consejos para evaluar expresiones algebraicas”, primero reemplace todas las ocurrencias de variables en la expresión con paréntesis abiertos.

\[ \frac{ad-bc}{a+b} = \frac{(~)(~)-(~)(~)}{(~)+(~)}\nonumber \]

En segundo lugar, sustituir cada variable por su valor dado, y tercero, seguir las “Reglas que guían el orden de operaciones” para evaluar la expresión resultante.

\[ \begin{aligned} \frac{ad-bc}{a+b} = \frac{( \textcolor{red}{5}) -( \textcolor{red}{-3}) ( \textcolor{red}{2})}{( \textcolor{red}{5}) + ( \textcolor{red}{-3})} ~ & \textcolor{red}{ \text{ Substitute: } 5 \text{ for } a,~ -3 \text{ for } b,~ 2 \text{ for } c,~ -4 \text{ for } d.} \\ = \frac{-20-(-6)}{2} ~ & \begin{aligned} \textcolor{red}{ \text{ Numerator: } (5)(=4)=-20,~ (-3)(2) = -6.} \\ \textcolor{red}{ \text{ Denominator: } 5+(-3)=2.} \end{aligned} \\ = \frac{-20+6}{2} ~ & \textcolor{red}{ \text{ Numerator: Add the opposite.}} \\ = \frac{-14}{2} ~ & \textcolor{red}{ \text{ Numerator: } -20+6=-14.} \\ = -7 ~ & \textcolor{red}{ \text{Divide.}} \end{aligned}\nonumber \]

Ejercicio

Si a = −7, b = −3, c = −15, 15 y d = −14, evalúe:

\[\frac{a^2+b^2}{c+d}\nonumber \]

Responder: −2

Ejemplo 6

A continuación se muestra un prisma rectangular.

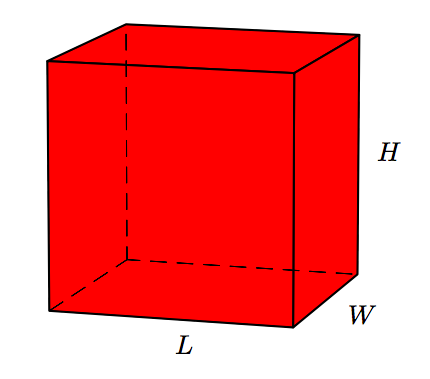
$Screen Shot 2019-08-19 at 6.09.16 PM.png$

El volumen del prisma rectangular viene dado por la fórmula

\[V=LWH,\nonumber \]

donde L es la longitud, W es el ancho y H es la altura del prisma rectangular. Encuentra el volumen de un prisma rectangular que tiene una longitud de 12 pies, un ancho de 4 pies y una altura de 6 pies.

Solución

Después de “Consejos para evaluar expresiones algebraicas”, primero reemplace todas las apariciones de L, W y H en la fórmula

\[ V = LWH\nonumber \]

con paréntesis abiertos.

\[V = (~)(~)(~)\nonumber \]

A continuación, sustituya 12 pies por L, 4 pies por W y 6 pies por H y simplifique.

\[ \begin{aligned} V = (12 \text{ft})(4 \text{ft})(6 \text{ft}) \\ = 288 \text{ft}^3 \end{aligned}\nonumber \]

De ahí que el volumen del prisma rectangular sea de 288 pies cúbicos.

Ejercicio

El área superficial del prisma representado en este ejemplo viene dada por la siguiente fórmula:

\[S = 2(W H + LH + LW) \nonumber \]

Si L = 12, W = 4 y H = 6 pies, respectivamente, calcule el área de superficie.

Responder: 288 pies cuadrados

Ejercicios

En los Ejercicios 1-12, evaluar la expresión al valor dado de x.

1. −3x ² − 6x + 3 a x = 7

2. 7x ² − 7x + 1 en x = −8

3. −6x − 6 en x = 3

4. 6x − 1 en x = −10

5. 5x ² + 2x + 4 en x = −1

6. 4x ² − 9x + 4 en x = −3

7. −9x − 5 en x = −2

8. −9x + 12 a x = 5

9. 4x ² + 2x + 6 a x = −6

10. −3x ² + 7x + 4 a x = −7

11. 12x + 10 a x = −12

12. −6x + 7 a x = 11

En los Ejercicios 13-28, evaluar la expresión a los valores dados de x e y.

13. |x|−|y| a x = −5 e y = 4

14. |x|−|y| en x = −1 e y = −2

15. −5x ² + 2y ² a x = 4 e y = 2

16. −5x ² − 4y ² a x = −2 e y = −5

17. |x|−|y| a x = 0 e y = 2

18. |x|−|y| en x = −2 e y = 0

19. |x − y| en x = 4 e y = 5

20. |x − y| en x = −1 e y = −4

21. 5x ² − 4xy + 3y ² a x = 1 e y = −4

22. 3x ² + 5xy + 3y ² a x = 2 e y = −1

23. |x − y| en x = 4 e y = 4

24. |x − y| en x = 3 e y = −5

25. −5x ² − 3xy + 5y ² a x = −1 e y = −2

26. 3x ² − 2xy − 5y ² a x = 2 e y = 5

27. 5x ² + 4y ² a x = −2 e y = −2

28. −4x ² + 2y ² a x = 4 e y = −5

En los Ejercicios 29-40, evaluar la expresión al valor dado de x.

29. $ \frac{9+9x}{−x}$a x = −3

30. $ \frac{9 − 2x}{−x}$a x = −1

31. $\frac{−8x + 9}{−9 + x}$a x = 10

32. $\frac{2x + 4}{1 + x}$a x = 0

33. $\frac{−4+9x}{7x}$a x = 2

34. $\frac{−1 − 9x}{x}$a x = −1

35. $\frac{−12 − 7x}{x}$a x = −1

36. $\frac{12 + 11x}{3x}$a x = −6

37. $\frac{6x − 10}{5}$+ x a x = −6

38. $\frac{11x + 11}{−4}$+ x a x = 5

39. $\frac{10x + 11}{5}$+ x a x = −4

40. $\frac{6x + 12}{−3}$+ x a x = 2

41. La fórmula

\[d=16t^2\nonumber \]

da la distancia (en pies) que un objeto cae del reposo en términos del tiempo t que ha transcurrido desde su liberación. Encuentra la distancia d (en pies) que cae un objeto en t = 4 segundos.

42. La fórmula

\[d = 16t^2\nonumber \]

da la distancia (en pies) que un objeto cae del reposo en términos del tiempo t que ha transcurrido desde su liberación. Encuentra la distancia d (en pies) a la que cae un objeto en t = 24 segundos.

43. La fórmula

\[C = \frac{5(F − 32)}{9}\nonumber \]

da la temperatura Celcio C en términos de la temperatura Fahrenheit F. Utilice la fórmula para encontrar la temperatura Celsius (◦ C) si la temperatura Fahrenheit es F = 230◦ F.

44. La fórmula

\[C = \frac{5(F − 32)}{9}\nonumber \]

da la temperatura Celcio C en términos de la temperatura Fahrenheit F. Utilice la fórmula para encontrar la temperatura Celsius (^◦ C) si la temperatura Fahrenheit es F = 95 ^◦ F.

45. La escala Kelvin de temperatura se utiliza en química y física. El cero absoluto ocurre a 0 ^◦ K, la temperatura a la que las moléculas tienen cero energía cinética. El agua se congela a 273 ^◦ K y hierve a K = 373 ^◦ K. Para cambiar la temperatura Kelvin a temperatura Fahrenheit, utilizamos la fórmula

\[F = \frac{9(K − 273)}{5} + 32.\nonumber \]

Usa la fórmula para cambiar 28 ^◦ K a Fahrenheit.

46. La escala Kelvin de temperatura se utiliza en química y física. El cero absoluto ocurre a 0 ^◦ K, la temperatura a la que las moléculas tienen cero energía cinética. El agua se congela a 273 ^◦ K y hierve a K = 373 ^◦ K. Para cambiar la temperatura Kelvin a temperatura Fahrenheit, utilizamos la fórmula

\[F = \frac{9(K − 273)}{5} + 32.\nonumber \]

Utilice la fórmula para cambiar 248 ^◦ K a Fahrenheit.

47. Se lanza una pelota verticalmente hacia arriba. Su velocidad t segundos después de su liberación viene dada por la fórmula

\[v = v0 − gt,\nonumber \]

donde v ₀ es su velocidad inicial, g es la aceleración debida a la gravedad, y v es la velocidad de la bola en el tiempo t. La aceleración por gravedad es g = 32 pies por segundo por segundo. Si la velocidad inicial de la pelota es v ₀ = 272 pies por segundo, encuentra la velocidad de la pelota después de t = 6 segundos.

48. Se lanza una pelota verticalmente hacia arriba. Su velocidad t segundos después de su liberación viene dada por la fórmula

\[v = v_0 − gt,\nonumber \]

donde v ₀ es su velocidad inicial, g es la aceleración debida a la gravedad, y v es la velocidad de la bola en el tiempo t. La aceleración por gravedad es g = 32 pies por segundo por segundo. Si la velocidad inicial de la pelota es v ₀ = 470 pies por segundo, encuentra la velocidad de la pelota después de t = 4 segundos.

49. Números pares. Evalúe la expresión 2n para los siguientes valores:

i) n = 1

ii) n = 2

iii) n = 3

iv) n = −4

v) n = −5

vi) ¿El resultado es siempre un número par? Explique.

50. Números impares. Evalúe la expresión 2n + 1 para los siguientes valores:

i) n = 1

ii) n = 2

iii) n = 3

iv) n = −4

v) n = −5

vi) ¿El resultado es siempre un número impar? Explicar.

RESPUESTAS

1. −186

3. −24

5. 7

7. 13

9. 138

11. −134

13. 1

15. −72

17. −2

19. 1

21. 69

23. 0

25. 9

27. 36

29. −6

31. −71

33. 1

35. 5

37. 46

39. −29

41. 256 pies

43. 110 grados

45. −409 ^◦ F

47. 80 pies por segundo

49.

i) 2

ii) 4

iii) 6

iv) −8

v) −10

vi) Sí, el resultado siempre será un número par porque 2 siempre será un factor del producto 2n.

Search

Text Color

Text Size

Margin Size

Font Type