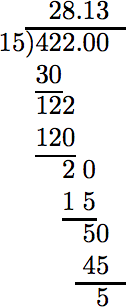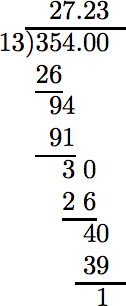6.2: Introducción a Ratios y Tarifas

Última actualización
Guardar como PDF

Page ID: 113455

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Utilizamos ratios para comparar dos cantidades numéricas o cantidades con las mismas unidades.

Ratio

Una relación es el cociente de dos cantidades numéricas o dos cantidades con las mismas unidades físicas.

Por ejemplo, los geometros griegos antiguos creían que el rectángulo más agradable al ojo tenía largo y ancho tal que la relación de largo a ancho era un número específico, llamado la Relación áurea, aproximadamente igual a 1.6180339887... Los arquitectos hasta el día de hoy utilizan esta proporción en sus diseños.

Hay varias formas equivalentes de expresar proporciones, tres de las cuales usaremos en este texto: notación de fracciones, notación “a” y notación de “dos puntos”.

3/4 es una relación, se lee como “la relación de 3 a 4”.
3 a 4 es una relación, se lee como “la relación de 3 a 4”.
3:4 es una relación, se lee como “la relación de 3 a 4”.

Ejemplo 1

Expresar cada una de las siguientes proporciones como fracción reducida a términos más bajos: (a) 36 a 24, y (b) 0.12:0.18.

Solución

a) Expresar la relación “36 a 24” como fracción, colocar 36 sobre 24 y reducir.

\[ \begin{aligned} \frac{36}{24} = \frac{3 \cdot \textcolor{red}{12}}{2 \cdot \textcolor{red}{12}} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{3 \cdot \cancel{ \textcolor{red}{12}}}{2 \cdot \cancel{ \textcolor{red}{12}}} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \\ = \frac{3}{2} \end{aligned}\nonumber \]

Así, la relación 36 a 24 es igual a 3/2.

b) Expresar la relación “0. 12:0 .18” como fracción, colocar 0.12 sobre 0.18 y reducir.

\[ \begin{aligned} \frac{0.12}{0.18} = \frac{(0.18) \textcolor{red}{(100)}}{(0.18) \textcolor{red}{(100)}} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 100.}} \\ = \frac{12}{18} ~ & \textcolor{red}{ \text{ Move each decimal 2 places right.}} \\ = \frac{2 \cdot \textcolor{red}{6}}{3 \cdot \textcolor{red}{6}} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{2 \cdot \cancel{ \textcolor{red}{6}}}{3 \cdot \cancel{ \textcolor{red}{6}}} ~ & \textcolor{red}{ \text{Cancel.}} \\ \frac{2}{3} \end{aligned}\nonumber \]

Así, la relación 0. 12:0 .18 equivale a 2/3.

Ejercicio

Express 0.12:0.3 como fracción reducida a términos más bajos.

Contestar: 2/5

Ejemplo 2

Para el rectángulo que sigue, exprese la relación de largo a ancho como una fracción reducida a términos más bajos.

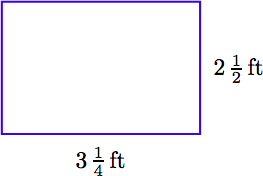
$imageedit_32_5126423827.png$

Solución.

La relación longitud a ancho puede expresarse como una fracción y reducirse de la siguiente manera.

\[ \begin{aligned} \frac{ \text{length}}{ \text{width}} = \frac{3 \frac{1}{4} \text{ ft}}{2 \frac{1}{2} \text{ ft}} ~ & \textcolor{red}{ \text{ Length to width as a fraction.}} \\ = \frac{3 \frac{1}{4} \cancel{ \text{ ft}}}{2 \frac{1}{2} \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{ \frac{13}{4}}{ \frac{5}{2}} ~ & \textcolor{red}{ \text{ Mixed to improper fractions.}} \end{aligned}\nonumber \]

Invertir y multiplicar, factorizar y cancelar factores comunes.

\[ \begin{aligned} = \frac{13}{4} \cdot \frac{2}{5} ~ & \textcolor{red}{ \text{ Invert and multiply.}} \\ = \frac{26}{20} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{13 \cdot \textcolor{red}{2}}{10 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Factor numerator and denominator.}} \\ = \frac{13 \cdot \cancel{ \textcolor{red}{2}}}{10 \cdot \cancel{ \textcolor{red}{2}}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{13}{10} \end{aligned}\nonumber \]

De ahí que la relación largo a ancho sea 13/10.

Ejercicio

Un rectángulo tiene$8 \frac{1}{4}$ pulgadas de largo y$3 \frac{1}{2}$ pulgadas de ancho. Expresar la relación de longitud a ancho como una fracción reducida a términos más bajos.

Contestar: 33/14

Tarifas

Ahora introducimos el concepto de tasa, un tipo especial de ratio.

Tarifa

Una tasa es un cociente de dos mediciones con diferentes unidades.

La interpretación física de una tasa en términos de sus unidades es una habilidad importante.

Ejemplo 3

Un automóvil viaja 224 millas con 12 galones de gasolina. Expresar la relación distancia recorrida al consumo de gas como una fracción reducida a los términos más bajos. Escribe una oración breve explicando el significado físico de tu solución. Incluya unidades en su descripción.

Solución

Colocar millas recorridas sobre galones de gasolina consumidos y reducir.

\[ \begin{aligned} \frac{224 \text{ mi}}{12 \text{ gal}} = \frac{56 \cdot \textcolor{red}{4} \text{ mi}}{3 \cdot \textcolor{red}{4} \text{ gal}} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{56 \cdot \cancel{ \textcolor{red}{4}} \text{ mi}}{3 \cdot \cancel{ \textcolor{red}{4}} \text{ gal}} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \\ = \frac{56 \text{ mi}}{3 \text{ gal}} \end{aligned}\nonumber \]

Así, la tarifa es de 56 millas a 3 galones de gasolina. En lenguaje sencillo, esto significa que el automóvil recorre 56 millas con 3 galones de gasolina.

Ejercicio

Lanny recorre 180 kilómetros con 14 litros de gasolina. Expresar la relación distancia recorrida al consumo de gas como una fracción reducida a los términos más bajos.

Contestar: 90/7 kilómetros por litro

Tarifas unitarias

A la hora de hacer comparaciones, es útil tener una tasa en una forma donde el denominador sea 1. A tales tarifas se les da un nombre especial.

Tasa Unitaria

Una tasa unitaria es una tasa cuyo denominador es 1.

Ejemplo 4

Herman conduce 120 millas en 4 horas. Encuentra su tasa promedio de velocidad.

Solución

Coloca la distancia recorrida en el tiempo que lleva conducir esa distancia.

\[ \begin{aligned} \frac{120 \text{ miles}}{4 \text{ hours}} = \frac{30 \text{ miles}}{1 \text{ hour}} ~ & \textcolor{red}{ \text{ Divide: } 120/4 = 30.} \\ = 30 \text{ miles/hour} \end{aligned}\nonumber \]

De ahí que la tasa promedio de velocidad de Herman sea de 30 millas por hora.

Ejercicio

Jacob conduce 120 kilómetros en 3 horas. Encuentra su tasa promedio de velocidad.

Contestar: 40 kilómetros por hora

Ejemplo 5

Aditya trabaja 8.5 horas y recibe 95 dólares por sus esfuerzos. ¿Cuál es su tarifa salarial por hora?

Solución

Coloquemos el dinero ganado sobre las horas trabajadas para obtener la siguiente tasa:

\[ \frac{95 \text{ dollars}}{8.5 \text{ hours}}\nonumber \]

Tendremos una idea mucho mejor de la tasa salarial de Aditya si expresamos la tasa con un denominador de 1. Para ello, divídanos. Empuje el decimal en el divisor hacia el extremo derecho, luego mueva el decimal un número igual de lugares en el dividendo. Como estamos tratando con dólares y centavos, redondearemos nuestra respuesta a la centésima más cercana.

$imageedit_20_5856924599.png$

Debido a que el dígito de prueba es mayor o igual a 5, agregamos 1 al dígito de redondeo y truncamos; es decir, 95/8.5 ≈ 11.18. Por lo tanto,

\[ \begin{aligned} \frac{95 \text{ dollars}}{8.5 \text{ hours}} = \frac{11.18 \text{ dollars}}{1 \text{ hour}} ~ & \textcolor{red}{ \text{ Divide: } 95/8.5 \approx 11.18.} \\ = 11.18 \text{ dollars/hour.} \end{aligned}\nonumber \]

Es decir, su tasa salarial es de 11.18 dólares por hora.

Ejercicio

Frannie trabaja 5.5 horas y recibe 120 dólares por sus esfuerzos. ¿Cuál es su tarifa salarial por hora? Redondee su respuesta al centavo más cercano.

Contestar: $21.82 por hora

Ejemplo 6

Un automóvil viaja 422 millas con 15 galones de gasolina. Un segundo automóvil viaja 354 millas con 13 galones de gasolina. ¿Qué automóvil obtiene el mejor kilometraje de gasolina?

Solución

La división decimal (redondeada a la décima más cercana) revela el mejor kilometraje de gasolina.

En el caso del primer automóvil, obtenemos la siguiente tarifa:

\[ \frac{422 \text{ mi}}{15 \text{gal}}\nonumber \]

Dividir.

$imageedit_24_9257583841.png$

A la décima más cercana, 28.1.

En el caso del segundo autombile, obtenemos la siguiente tasa:

\[ \frac{354 \text{ mi}}{13 \text{ gal}}\nonumber \]

Dividir.

$imageedit_28_6744192722.png$

A la décima más cercana, 27.2.

En el caso del primer automóvil, la tasa de kilometraje es de 28.1 mi/1 gal, que se puede leer “28.1 millas por galón”. En el caso del segundo automóvil, la tasa de kilometraje es de 27.2 mi/1 gal, que se puede leer “27.2 millas por galón”. Por lo tanto, el primer automóvil obtiene el mejor kilometraje de gasolina.

Ejercicio

Alicia trabaja 8 horas y gana $100. Connie trabaja 10 horas y gana $122. ¿Qué mujer trabaja a la tarifa por hora más grande?

Contestar: Alicia

Ejercicios

En los Ejercicios 1-24, expresar la proporción dada como una fracción reducida a los términos más bajos.

1. 0.14:0.44

2. 0.74:0.2

3. 0.05:0.75

4. 0.78:0.4

5. 0. 1:0 .95

6. 0.93:0.39

7. $2 \frac{2}{9}$:$1 \frac{1}{3}$

8. $3 \frac{2}{3} : 2 \frac{4}{9}$

9. 0.36:0.6

10. 0.58:0.42

11. 15:21

12. 77:121

13. $2 \frac{8}{9}$:$2 \frac{2}{3}$

14. $1 \frac{2}{3}$:$3 \frac{8}{9}$

15. $3 \frac{8}{9}$:$2 \frac{1}{3}$

16. $1 \frac{5}{9}$:$1 \frac{1}{3}$

17. $2 \frac{5}{8}$:$1 \frac{3}{4}$

18. $2 \frac{4}{9}$:$1 \frac{1}{3}$

19. 10:35

20. 132:84

21. 9:33

22. 35:10

23. 27:99

24. 12:28

25. Un automóvil viaja 271.8 millas con 10.1 galones de gasolina. Un segundo automóvil viaja 257.9 millas con 11.1 galones de gasolina. ¿Qué automóvil obtiene el mejor kilometraje de gasolina?

26. Un automóvil viaja 202.9 millas con 13.9 galones de gasolina. Un segundo automóvil viaja 221.6 millas con 11.8 galones de gasolina. ¿Qué automóvil obtiene el mejor kilometraje de gasolina?

27. A Todd se le paga 183 dólares por 8.25 horas de trabajo. ¿Cuál es su salario por hora, redondeado al centavo más cercano?

28. A David se le pagan 105 dólares por 8.5 horas de trabajo. ¿Cuál es su salario por hora, redondeado al centavo más cercano?

29. Un automóvil recorre 140 millas en 4 horas. Encuentra la tasa promedio de velocidad.

30. Un automóvil recorre 120 millas en 5 horas. Encuentra la tasa promedio de velocidad.

31. A Judá se le pagan 187 dólares por 8 horas de trabajo. ¿Cuál es su salario por hora, redondeado al centavo más cercano?

32. A Judá se le paga 181 dólares por 8.75 horas de trabajo. ¿Cuál es su salario por hora, redondeado al centavo más cercano?

33. Un automóvil viaja 234.2 millas con 10.8 galones de gasolina. Un segundo automóvil viaja 270.5 millas con 10.8 galones de gasolina. ¿Qué automóvil obtiene el mejor kilometraje de gasolina?

34. Un automóvil viaja 297.6 millas con 10.7 galones de gasolina. Un segundo automóvil viaja 298.1 millas con 12.6 galones de gasolina. ¿Qué automóvil obtiene el mejor kilometraje de gasolina?

35. Un automóvil recorre 180 millas en 5 horas. Encuentra la tasa promedio de velocidad.

36. Un automóvil recorre 220 millas en 5 horas. Encuentra la tasa promedio de velocidad.

37. Trekking antártico. Siete mujeres en una caminata de esquí antártico de 562-millas llegaron al Polo Sur 38 días después de que comenzaran su aventura. ¿Cuál era la tasa promedio de velocidad por día de las mujeres? Redondee su resultado a la décima de milla más cercana. Associated Press-Times-Standard 12/31/09 Después de una caminata de esquí de 561 millas, siete mujeres llegan al Polo Sur.

RESPUESTAS

1. $\frac{7}{22}$

3. $\frac{1}{15}$

5. $\frac{2}{19}$

7. $\frac{5}{3}$

9. $\frac{3}{5}$

11. $\frac{5}{7}$

13. $\frac{13}{12}$

15. $\frac{5}{3}$

17. $\frac{3}{2}$

19. $\frac{2}{7}$

21. $\frac{3}{11}$

23. $\frac{3}{11}$

25. El primer automóvil tiene el mejor kilometraje por galón.

27. 22.18 dólares/hr

29. 35 mi/h

31. 23.38 dólares/hr

33. El segundo automóvil tiene el mejor kilometraje por galón.

35. 36 mi/h

37. 14.8 millas por día