6.3: Introducción a la Proporción

Última actualización
Guardar como PDF

Page ID: 113449

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la Sección 6.1, se introdujeron los conceptos o ratio y tasa. En esta sección, equiparamos estas proporciones en un constructo llamado proporción.

Proporciones

Una proporción es una declaración que iguala dos ratios o tasas.

Por ejemplo, cada una de las ecuaciones

\[\frac{1}{3} = \frac{2}{6}, ~ \frac{15 \text{ miles}}{2 \text{ hours}} = \frac{30 \text{ miles}}{4 \text{ hours}}, \text{ and } \frac{a}{b} = \frac{c}{d}\nonumber \]

comparar dos ratios o tasas y es una proporción.

La proporción

\[ \frac{1}{3} = \frac{2}{6}\nonumber \]

se lee “uno es a tres como dos es a seis”. Los cuatro números que componen esta proporción se denominan términos de la proporción y se ordenan de manera natural.

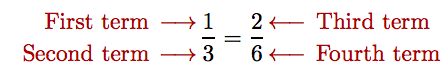
$Screen Shot 2019-09-18 en 2.43.31 PM.png$

Extremos y Medios

El primer y cuarto término se denominan los extremos de la proporción. El segundo y tercer término se denominan las medias de la proporción.

En la proporción

\[ \frac{a}{b} = \frac{c}{d},\nonumber \]

los términos a y d son los extremos; los términos b y c son las medias.

$Screen Shot 2019-09-18 en 2.45.27 PM.png$

Si multiplicamos ambos lados de la proporción por el denominador común,

\[bd \left(\frac{a}{b} \right) = bd \left( \frac{c}{d} \right)\nonumber \]

luego cancelar,

\[ \cancel{b} d \left( \frac{a}{\cancel{b}} \right) = b \cancel{d} \left( \frac{c}{\cancel{d}} \right)\nonumber \]

obtenemos el siguiente resultado.

\[ad = bc\nonumber \]

Esto lleva a la siguiente observación.

Producto de Extremos y Medios

En la proporción

\[ \frac{a}{b} = \frac{c}{d}\nonumber \]

el producto de las medias es igual al producto de los extremos. Es decir,

\[ad = bc.\nonumber \]

Podemos obtener un resultado equivalente usando una técnica llamada multiplicación cruzada.

$Screen Shot 2019-09-18 en 2.49.15 PM.png$

Ejemplo 1

Cuál de las siguientes proporciones es válida: a)$\frac{2}{3} = \frac{7}{12}$, o b)$\frac{4}{9} = \frac{12}{27}$.

Solución

(a) Multiplicar cruz

$Screen Shot 2019-09-18 en 2.52.15 PM.png$

para obtener

24 = 21.

De ahí que el producto de los extremos no sea igual al producto de las medias, por lo que 2/3=7/12 no es una proporción válida.

b) Multiplicar en cruz

$Screen Shot 2019-09-18 en 2.52.20 PM.png$

para obtener

108 = 108.

De ahí que el producto de los extremos sea igual al producto de las medias, por lo que 4/9 = 12/27 es una proporción válida.

Ejercicio

¿Es válida la siguiente proporción? $\frac{4}{3} = \frac{16}{11}$

Contestar: No

Resolviendo Proporciones

Ya tenemos todas las herramientas necesarias para resolver proporciones. Empecemos por el primer ejemplo.

Ejemplo 2

Resolver la proporción para x:$\frac{3}{4} = \frac{x}{12}$.

Solución

Cruzar multiplicar, luego resolver la ecuación resultante.

\[ \begin{aligned} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 4 \cdot x = 3 \cdot 12 ~ & \textcolor{red}{ \text{ Products of means and extremes are equal.}} \\ 4x = 36 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{4x}{4} = \frac{36}{4} ~ & \textcolor{red}{ \text{ Divide both sides by 4.}} \\ x = 9 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Cheque

Sustituye 9 por x en la proporción original y verifica.

\[ \begin{aligned} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ \frac{3}{4} = \frac{9}{12} ~ & \textcolor{red}{ \text{ Substitute 9 for } x.} \end{aligned}\nonumber \]

Multiplicar cruz.

$Screen Shot 2019-09-18 en 2.58.18 PM.png$

Así, la solución 9 comprueba.

Ejercicio

Resolver la proporción para n:$\frac{2}{3} = \frac{n}{9}$

Contestar: 6

Ejemplo 3

Resolver la proporción para n:$\frac{3}{2} = \frac{24}{n}$.

Solución

Cruzar multiplicar, luego resolver la ecuación resultante.

\[ \begin{aligned} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 3 \cdot n = 2 \cdot 24 ~ & \textcolor{red}{ \text{ Products of means and extremes are equal.}} \\ 3n = 48 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{3n}{3} = \frac{48}{3} ~ & \textcolor{red}{ \text{ Divide both sides by 3.}} \\ n = 16 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Cheque

Sustituir 16 por n en la proporción original y verificar.

\[ \begin{aligned} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ \frac{3}{2} = \frac{24}{16} ~ & \textcolor{red}{ \text{ Substitute 16 for } n.} \end{aligned}\nonumber \]

Multiplicar cruz.

$Screen Shot 2019-09-18 en 2.58.28 PM.png$

Así, la solución 16 comprueba.

Ejercicio

Resolver la proporción para m:$\frac{9}{6} = \frac{m}{4}$

Contestar: 6

Ejemplo 4

Resolver la proporción para x:$\frac{2x + 1}{15} = \frac{1}{3}$.

Solución

Cruzar multiplicar, luego resolver la ecuación resultante.

\[ \begin{aligned} \frac{2x+1}{15} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 3(2x+1) = 15(1) ~ & \textcolor{red}{ \text{ Products f means and extremes are equal.}} \\ 6x+3 = 15 ~ & \textcolor{red}{ \begin{aligned} \text{ On the left, distribute.} \\ \text{ On the right, multiply.} \end{aligned}} \\ 6x+3-3=15-3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 6x=12 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{6x}{6} = \frac{12}{6} ~ & \textcolor{red}{ \text{ Divide both sides by 6.}} \\ x = 2 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Cheque

Dejaremos que nuestros lectores comprueben esta solución.

Ejercicio

Resolver la proporción para y:$\frac{6+2y}{18} = \frac{8}{9}$

Contestar: 5

Aplicaciones

Una serie de aplicaciones prácticas implican resolver una proporción.

Ejemplo 5

Si 5 naranjas cuestan $1.15, ¿cuál será el costo de 15 naranjas (asumiendo una tasa igual)?

Solución

Dejar x representar el costo de 15 naranjas. Suponiendo que la tasa para 5 naranjas en $1.15 es igual a la tasa para 15 naranjas a un costo desconocido x, establecemos la siguiente proporción.

\[ \frac{5}{1.15} = \frac{15}{x}\nonumber \]

Multiplicar cruz

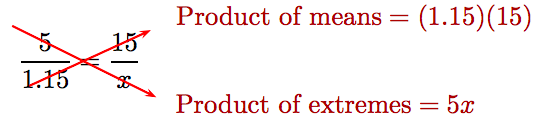
$Screen Shot 2019-09-18 en 2.58.39 PM.png$

para obtener

\[5x = 17.25.\nonumber \]

Resolver para x.

\[\begin{aligned} \frac{5x}{5} = \frac{17.25}{5} \\ x = 3.45 \end{aligned}\nonumber \]

Así, 15 naranjas cuestan $3.45.

Ejercicio

Si 7 manzanas cuestan $3.15, ¿cuánto costarán 10 manzanas (asumiendo una tasa igual)?

Contestar: $4.50

Verificar unidades es extremadamente importante

Al establecer una proporción, verifique que ambos numeradores tengan las mismas unidades y que ambos denominadores tengan las mismas unidades.

Por ejemplo, en el Ejemplo 5, ambos numeradores tienen “naranjas” como unidades y ambos denominadores tienen “dólares” como unidades.

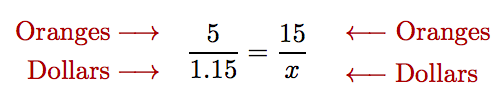
$Screen Shot 2019-09-18 en 2.58.50 PM.png$

Esta proporción se configura correctamente, porque ambos numeradores tienen las mismas unidades y ambos denominadores tienen las mismas unidades. Por otro lado, si hubiéramos establecido la proporción incorrectamente de la siguiente manera,

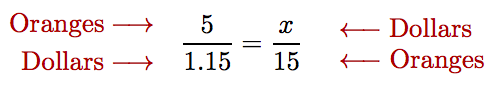
$Captura de pantalla 2019-09-18 en 2.58.56 PM.png$

una comprobación rápida de las unidades revela el error; es decir, los numeradores tienen diferentes unidades y los denominadores tienen diferentes unidades. ¡Comprobando unidades nos ayuda a evitar errores!

Ejemplo 6

Dylan y David están planeando un viaje de mochilero en el Parque Nacional Yosemite. En su mapa, la leyenda indica que 1.2 centímetros representan 2 millas. ¿Cuánto tiempo dura su viaje si la ruta mide 10.6 centímetros en el mapa? Redondee su respuesta a la décima de milla más cercana.

Solución

Vamos a establecer la proporción con unidades.

\[\frac{1.2 \text{ cm}}{2 \text{ mi}} = \frac{10.6 \text{ cm}}{x \text{ mi}}\nonumber \]

Observe cómo incluir las unidades ayuda en la configuración de la proporción. Ahora, dejemos caer las unidades y resolvamos para x.

\[ \begin{aligned} \frac{1.2}{2} = \frac{10.6}{x} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 1.2x = (2)(10.6) ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ 1.2x = 21.2 ~ & \textcolor{red}{ \text{ Simplify right-side hand.}} \\ \frac{1.2x}{1.2} = \frac{21.2}{1.2} ~ & \textcolor{red}{ \text{ Divide both sides by 1.2.}} \\ x \approx 17.66 ~ & \textcolor{red}{ \text{ On the right: Divide.}} \end{aligned}\nonumber \]

Llevamos la división de la derecha un decimal más allá del décimo lugar. El dígito de redondeo es un 6 y el siguiente dígito de prueba es un 6. Agrega 1 al dígito de redondeo y trunca.

A la décima de milla más cercana, la ruta de mochilero es aproximadamente de 17.7 millas.

Ejercicio

Eloise y Susannah están planeando un viaje es el Parque Nacional Sequoia. En su mapa, 3 pulgadas representa 50 millas. ¿Cuánto dura su viaje si la ruta mide$4 \frac{1}{2}$ pulgadas en el mapa?

Contestar: 75 millas

Ejemplo 7

Una receta para hacer 2 docenas de galletas requiere$1 \frac{3}{4}$ tazas de harina, entre otros ingredientes. Si el panadero desea hacer el doble de esa cantidad de galletas, ¿cuánta harina se requiere?

Solución

Dos veces 2 docenas son 4 docenas de galletas. Dejar x representar la cantidad de harina necesaria para 4 docenas de galletas. Asumiendo una tasa igual para 2 docenas de galletas (2 docenas requiere 1 3 4 tazas de harina), configuramos la siguiente proporción. Nuevamente, el uso de unidades nos ayuda a elaborar la proporción correcta.

\[\frac{2 \text{ dozen}}{1 \frac{3}{4} \text{ cups}} = \frac{4 \text{ dozen}}{x \text{ cups}}\nonumber \]

Observe cómo incluir las unidades ayuda en la configuración de la proporción. Ahora, dejemos caer las unidades y resolvamos para x.

\[ \begin{aligned} \frac{2}{1 \frac{3}{4}} = \frac{4}{x} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 2x = 1 \frac{3}{4} \cdot 4 ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ 2x = \frac{7}{4} \cdot 4 ~ & \textcolor{red}{ \text{ Change to improper fraction.}} \\ 2x = 7 ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Divide ambos lados de la ecuación por 2 y termina.

\[ \begin{aligned} \frac{2x}{2} = \frac{7}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = \frac{7}{2} \end{aligned}\nonumber \]

Cambiar la fracción impropia a una fracción mixta. Así, se necesitarán$3 \frac{1}{2}$ tazas de harina para hacer 4 docenas de galletas.

Ejercicio

La masa para 3 pizzas requiere$8 \frac{1}{2}$ tazas de harina. Si el panadero desea hacer 9 pizzas, ¿cuántas tazas de harina se requieren?

Contestar: $25 \frac{1}{2}$tazas

Ejercicios

En los Ejercicios 1-12, ¿cuál de los siguientes es una verdadera proporción?

1. $\frac{9}{7} = \frac{27}{21}, ~ \frac{4}{3} = \frac{9}{7}, ~ \frac{7}{2} = \frac{8}{9}, ~ \frac{4}{8} = \frac{9}{6}$

2. $\frac{6}{7} = \frac{18}{21}, ~ \frac{2}{3} = \frac{8}{6}, ~ \frac{4}{3} = \frac{3}{2}, ~ \frac{8}{9} = \frac{3}{8}$

3. $\frac{7}{6} = \frac{28}{24}, ~ \frac{5}{6} = \frac{5}{4}, ~ \frac{9}{5} = \frac{7}{3}, ~ \frac{9}{2} = \frac{8}{9}$

4. $\frac{7}{6} = \frac{2}{8}, ~ \frac{4}{5} = \frac{5}{7}, ~ \frac{3}{4} = \frac{15}{20}, ~ \frac{8}{4} = \frac{8}{7}$

5. $\frac{6}{5} = \frac{24}{20}, ~ \frac{7}{3} = \frac{2}{4}, ~ \frac{2}{4} = \frac{2}{6}, ~ \frac{5}{2} = \frac{2}{8}$

6. $\frac{9}{8} = \frac{4}{3}, ~ \frac{5}{7} = \frac{10}{14}, ~ \frac{8}{6} = \frac{5}{4}, ~ \frac{8}{5} = \frac{2}{6}$

7. $\frac{3}{5} = \frac{2}{8}, ~ \frac{3}{7} = \frac{6}{14}, ~ \frac{5}{6} = \frac{2}{4}, ~ \frac{7}{4} = \frac{5}{9}$

8. $\frac{7}{3} = \frac{7}{6}, ~ \frac{4}{7} = \frac{8}{14}, ~ \frac{5}{3} = \frac{7}{8}, ~ \frac{5}{7} = \frac{6}{9}$

9. $\frac{5}{4} = \frac{25}{20}, ~ \frac{9}{3} = \frac{9}{6}, ~ \frac{7}{4} = \frac{3}{6}, ~ \frac{3}{5} = \frac{9}{4}$

10. $\frac{7}{6} = \frac{6}{9}, ~ \frac{7}{3} = \frac{2}{5}, ~ \frac{6}{7} = \frac{30}{35}, ~ \frac{4}{7} = \frac{2}{8}$

11. $\frac{9}{7} = \frac{4}{3}, ~ \frac{9}{4} = \frac{7}{9}, ~ \frac{3}{5} = \frac{6}{10}, ~ \frac{3}{9} = \frac{9}{5}$

12. $\frac{4}{3} = \frac{8}{7}, ~ \frac{2}{6} = \frac{5}{8}, ~ \frac{7}{2} = \frac{3}{6}, ~ \frac{9}{4} = \frac{36}{16}$

En los Ejercicios 13-36, resuelve la proporción dada.

13. $\frac{17}{3} = \frac{x}{18}$

14. $\frac{16}{5} = \frac{x}{20}$

15. $\frac{6x + 10}{6} = \frac{11}{3}$

16. $\frac{4x + 8}{12} = \frac{5}{3}$

17. $\frac{17}{9} = \frac{x}{18}$

18. $\frac{8}{9} = \frac{x}{18}$

19. $\frac{11}{2} = \frac{x}{8}$

20. $\frac{11}{4} = \frac{x}{8}$

21. $\frac{7x + 15}{15} = \frac{10}{3}$

22. $\frac{7x + 3}{8} = \frac{5}{4}$

23. $\frac{11}{2} = \frac{x}{10}$

24. $\frac{19}{6} = \frac{x}{18}$

25. $\frac{5x + 8}{12} = \frac{2}{3}$

26. $\frac{3x + 12}{6} = \frac{3}{2}$

27. $\frac{2}{15} = \frac{24}{x}$

28. $\frac{7}{8} = \frac{14}{x}$

29. $\frac{3}{16} = \frac{6}{x}$

30. $\frac{4}{21} = \frac{12}{x}$

31. $\frac{5}{22} = \frac{20}{x}$

32. $\frac{3}{22} = \frac{21}{x}$

33. $\frac{2x + 10}{6} = \frac{14}{3}$

34. $\frac{2x + 9}{9} = \frac{13}{3}$

35. $\frac{7}{2} = \frac{21}{x}$

36. $\frac{2}{15} = \frac{18}{x}$

37. Si 13 huesos de perro cuestan $1.97, ¿cuál será el costo de 7 huesos de perro (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

38. Si 2 sandías cuestan $3.89, ¿cuál será el costo de 11 sandías (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

39. Si 7 bananos cuestan $2.55, ¿cuál será el costo de 14 bananos (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

40. Si 2 manzanas cuestan $2.05, ¿cuál será el costo de 8 manzanas (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

41. Si 13 naranjas cuestan $3.61, ¿cuál será el costo de 11 naranjas (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

42. Si 3 sandías cuestan $1.05, ¿cuál será el costo de 9 sandías (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

43. Si 3 huesos de perro cuestan $1.23, ¿cuál será el costo de 13 huesos de perro (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

44. Si 3 sandías cuestan $4.41, ¿cuál será el costo de 7 sandías (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

45. Si 3 manzanas cuestan $3.24, ¿cuál será el costo de 13 manzanas (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

46. Si 6 manzanas cuestan $3.43, ¿cuál será el costo de 7 manzanas (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

47. Si 4 huesos de perro cuestan $1.03, ¿cuál será el costo de 8 huesos de perro (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

48. Si 4 naranjas cuestan $4.28, ¿cuál será el costo de 3 naranjas (asumiendo una tasa igual)? Redondee su respuesta al centavo más cercano.

49. Dos rollos. En Haití, dos rollos planos cuestan 5 gourdes, alrededor de 12 centavos. ¿Cuántos centavos costarían 20 rollos? Associated Press-Times-Standard 02/18/10 Los campamentos sísmicos de Haití se convierten en barrios de chabolas.

50. Turbinas. Según lo propuesto, el proyecto Shell Wind Energy consiste en 25 turbinas con cima de crestas que pueden generar hasta 50 megavatios, o lo suficiente para suministrar electricidad a aproximadamente 1, 000 hogares. Estimar el número de turbinas crestas que se necesitarían para suministrar electricidad a 70, 000 viviendas, el número aproximado de propiedades en el condado de Humboldt, CA. John Driscoll Times-Standard 12/24/09 Proyecto de energía eólica se analiza.

51. Camiones volquetes. La autopista 199 de Estados Unidos tuvo un deslizamiento de tierra donde hasta 3, 000 yardas cúbicas de material cayeron sobre la carretera, requiriendo al parecer alrededor de 200 camiones volquetes grandes para retirar. Apenas una semana antes, 40, 000 yardas cúbicas de material cayeron sobre la Carretera 96. Estimar el número de volquetes necesarios para esa diapositiva redondeada al número entero más cercano. Associated Prensa-Times-Estándar 03/09/10 Otra autopista cerrada por tobogán.

52. Venta de madera. El plan Forestal Nacional Tongass de 26, 000 millas cuadradas de Alaska permite ventas de madera de hasta 267 millones de pies tablares por año, lo suficiente para casi 27, 000 viviendas de dos dormitorios, pero la demanda de madera es muy inferior a eso. Menos de 25 millones de pies tablares se registraron en el bosque en 2009. Funcionarios del Servicio Forestal han dicho que esperan aumentar la tala en el Tongass a unos 100 millones de pies tablares por año. Associated Press-Times-Standard 02/18/10 Industria pierde demanda por tala en Alaska.

i) Estimar el número de viviendas de 2 dormitorios que construirían 25 millones de pies de madera.

ii) ¿Cuántas casas de 2 dormitorios construirían 100 millones de pies de madera?

53. Derrame costoso. En Australia, las sanciones a los buques que causan derrames de petróleo son de aproximadamente 1.75 millones de dólares australianos, equivalentes a alrededor de $1.64 millones de dólares estadounidenses. Después de que un petrolero fue puesto a tierra en un arrecife de coral, funcionarios australianos están considerando elevar la multa a 10 millones de dólares australianos. ¿Cuál será la nueva multa en dólares estadounidenses? Redondee su respuesta a la centésima de millón de dólares más cercana. Associated Press-Times-Standard 04/13/10 Se eliminó el barco que filtró petróleo en la Gran Barrera de Coral.

RESPUESTAS

1. $\frac{9}{7} = \frac{27}{21}$es una proporción

3. $\frac{7}{6} = \frac{28}{24}$es una proporción

5. $\frac{6}{5} = \frac{24}{20}$es una proporción

7. $\frac{3}{7} = \frac{6}{14}$es una proporción

9. $\frac{5}{4} = \frac{25}{20}$es una proporción

11. $\frac{3}{5} = \frac{6}{10}$es una proporción

13. 102

15. 2

17. 34

19. 44

21. 5

23. 55

25. 0

27. 180

29. 32

31. 88

33. 9

35. 6

37. $1.06

39. $5.10

41. 3,05$

43. $5.33

45. 14.04$

47. $2.06

49. $0.48

51. 2, 667 cargas

53. $9.37 millones de dólares americanos