6.4: Conversión de Unidades - Sistema Americano

Última actualización
Guardar como PDF

Page ID: 113448

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección desarrollaremos una técnica para convertir unidades utilizadas en el sistema americano. Comenzamos con una discusión sobre las medidas comunes de longitud en los Estados Unidos.

Unidades de Largo

Las unidades de longitud más comunes son la pulgada, pie, yarda y milla. Nuestro enfoque estará en la técnica utilizada para convertir de una unidad de longitud a otra.

Unidades americanas de longitud

Hechos relativos a unidades comunes de longitud.

1 pie (ft) = 12 pulgadas (pulg.)
1 yarda (yd) = 3 pies (ft)
1 milla (mi) = 5280 pies (ft)

Tomemos por ejemplo, el hecho de que hay 3 pies en 1 yarda, lo que se puede afirmar como una ecuación, usando las abreviaturas comunes para pies (ft) y yardas (yd).

3 pies = 1 m

Si dividimos ambos lados de la ecuación por 3 pies,

\[ \frac{3 \text{ ft}}{3 \text{ ft}} = \frac{1 \text{ yd}}{3 \text{ ft}}, \nonumber\nonumber \]

o equivalentemente,

\[1 = \frac{1 \text{ yd}}{3 \text{ ft}}. \nonumber\nonumber \]

La observación clave es el hecho de que la relación 1 yd/3 ft es igual al número 1. En consecuencia, multiplicar por el “factor de conversión” 1 yd/3 ft equivale a multiplicar por 1. Esto se puede usar para cambiar una medida en pies a yardas.

Ejemplo 1

Cambia 36 pies a yardas.

Solución

Multiplique por el factor de conversión 1 yd/3 ft.

\[ \begin{aligned} 36 \text{ ft} = 36 \text{ ft} \cdot 1 ~ & \textcolor{red}{ \text{ Multiplicative Identity Property.}} \\ = 36 \text{ ft} \cdot \frac{1 \text{ yd}}{3 \text{ ft}} ~ & \textcolor{red}{ \text{ Replace 1 with 1 yd/3 ft.}} \\ = 36 \cancel{ \text{ ft}} \cdot \frac{1 \text{ yd}}{3 \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common unit.}} \\ = \frac{36 \cdot 1}{3} \text{ yd} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = \frac{36}{3} \text{ yd} ~ & \textcolor{red}{ \text{ Simplify.}} \\ = 12 \text{ yd} ~ & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]

De ahí que 36 pies equivalen a 12 yardas.

Ejercicio

Cambia 81 pies a yardas.

Contestar: 27 yardas

Por otro lado, podemos empezar de nuevo con

\[3 \text{ ft} = 1 \text{ yd}\nonumber \]

y dividir ambos lados de la ecuación por 1 yd.

\[\frac{3 \text{ ft}}{1 \text{ yd}} = \frac{1 \text{ yd}}{1 \text{ yd}} \nonumber\nonumber \]

Esto da el factor de conversión

\[ \frac{3 \text{ ft}}{1 \text{ yd}} = 1.\nonumber\nonumber \]

La observación clave es el hecho de que la relación 3 pies/1 yd es igual al número 1. En consecuencia, multiplicar por el “factor de conversión” 3 pies/1 yd equivale a multiplicar por 1. Esto se puede usar para cambiar una medida en yardas a pies.

Ejemplo 2

Cambia 18 yardas a pies.

Solución

Multiplicar por el factor de conversión 3 pies/1 yd.

\[ \begin{aligned} 18 \text{ yd} = 18 \text{ yd} \cdot 1 ~ & \textcolor{red}{ \text{ Multiplicative Identity Property.}} \\ = 18 \text{ yd} \cdot \frac{1 \text{ ft}}{1 \text{ yd}} ~ & \textcolor{red}{ \text{ Replace 1 with 3 ft/1 yd.} \\ = 18 \cancel{ \text{ yd}} \cdot \frac{3 \text{ ft}}{1 \cancel{ \text{ yd}} ~ & \textcolor{red}{ \text{ Cancel common unit.}} \\ = \frac{18 \cdot 3}{1} \text{ ft} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 54 \text{ ft} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

De ahí que 18 yardas equivalen a 54 pies.

Ejercicio

Cambia 15 yardas a pies.

Contestar: 45 pies

Otra comparación común es el hecho de que hay 12 pulgadas en 1 pie. Esto se puede representar como una ecuación usando la abreviatura común para pulgadas (in) y pies (ft).

\[12 \text{ in} = 1 \text{ ft}\nonumber \]

Dividiendo ambos lados por 12 pulgadas

\[ \frac{12 \text{ in}}{12 \text{ in}} = \frac{1 \text{ ft}}{12 \text{ in}},\nonumber \]

produce el factor de conversión

\[1 = \frac{1 \text{ ft}}{12 \text{ in}}.\nonumber \]

La observación clave es el hecho de que la relación 1 pies/12 in es igual al número 1. En consecuencia, multiplicar por el “factor de conversión” 1 pies/12 in equivale a multiplicar por 1. Esto se puede usar para cambiar una medida en pulgadas a pies.

Ejemplo 3

Cambiar 24 pulgadas a pies.

Solución

Multiplique por el factor de conversión 1 pies/12 in.

\[ \begin{aligned} 24 \text{ in} = 24 \text{ in} \cdot 1 ~ & \textcolor{red}{ \text{ Multiplicative Identity Property.}} \\ = 24 \text{ in} \cdot \frac{1 \text{ ft}}{12 \text{ in}} ~ & \textcolor{red}{ \text{ Replace 1 with 1 ft/12 in.}} \\ = 24 \cancel{ \text{ in}} \cdot \frac{1 \text{ in}}{12 \cancel{ \text{ in}}} ~ & \textcolor{red}{ \text{ Cancel common unit.}} \\ = \frac{24 \cdot 1}{12} \text{ ft} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 2 \text{ ft} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Por lo tanto, 24 pulgadas equivale a 2 pies.

Ejercicio

Cambia 48 pulgadas a pies.

Contestar: 4 pies

Ofrecemos un resumen de los factores de conversión para unidades de longitud en la Tabla 6.1.

Cuadro 6.1: Factores de conversión para unidades de longitud.
Convertir	Factor de conversión	Convertir	Factor de conversión
pies a pulgadas	12 pulgadas/1 pie	pulgadas a pies	1 pies/12 in
yardas a pies	3 pies/1 yarda	pies a yardas	1 yarda/3 pies
millas a pies	5280 ft/1 mi	pies a millas	1 mi/5280 ft

Algunas conversiones requieren más de una aplicación de un factor de conversión.

Ejemplo 4

Cambia 4 yardas a pulgadas.

Solución

Multiplicamos por una cadena de factores de conversión, el primero en cambiar yardas a pies, el segundo en cambiar pies a pulgadas.

\[ \begin{aligned} 4 \text{ yd} = 4 \text{ yd} \cdot \frac{3 \text{ ft}}{1 \text{ yd}} \cdot \frac{12 \text{ in}}{1 \text{ ft}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 4 \cancel{ \text{ yd}} \cdot \frac{3 \cancel{ \text{ ft}}{1 \cancel{ \text{ yd}} \cdot \frac{12 \text{ in}}{1 \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{4 \cdot 3 \cdot 12}{1 \cdot 1} \text{ in} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 144 \text{ in} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

De ahí que 4 yardas equivalen a 144 pulgadas.

Ejercicio

Cambia 8 yardas a pulgadas.

Contestar: 288 pulgadas

Ejemplo 5

Cambia 2 millas a yardas.

Solución

Multiplicamos por una cadena de factores de conversión, el primero en cambiar millas a pies, el segundo en cambiar pies a yardas.

\[ \begin{aligned} 2 \text{ mi} = 2 \text{ mi} \cdot \frac{5280 \text{ ft}}{1 \text{ mi}} \cdot \frac{1 \text{ yd}}{3 \text{ ft}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 2 \cancel{ \text{ mi}} \cdot \frac{5280 \cancel{ \text{ ft}}}{1 \cancel{ \text{ mi}}} \cdot \frac{1 \text{ yd}}{3 \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{2 \cdot 5280 \cdot 1}{1 \cdot 3} \text{ yd} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 3520 \text{ yd} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

De ahí que 2 millas equivalen a 3,520 yardas.

Ejercicio

Cambiar 5 millas a yardas.

Contestar: 8,800 yardas

Unidades de Peso

Las unidades de peso más comunes son la onza, la libra y la tonelada. Nuestro enfoque se mantendrá en cómo convertir de una unidad a otra.

Unidades americanas de peso

Hechos relativos a unidades comunes de peso.

1 libra (lb) = 16 onzas (oz)
1 tonelada = 2000 libras (lb)

Los hechos anteriores conducen a los factores de conversión en el Cuadro 6.2.

Cuadro 6.2: Factores de conversión para unidades de peso.
Convertir	Factor de conversión	Convertir	Factor de conversión
libras a onzas	16 oz/1 lb	onzas a libras	1 lb/16 oz
toneladas a libras	2000 lb/1 tonelada	libras a toneladas	1 ton/2000 lb

Ejemplo 6

Cambia$2 \frac{1}{2}$ libras a onzas.

Solución

Multiplicar por el factor de conversión apropiado.

\[ \begin{aligned} 2 \frac{1}{2} \text{ lb} = 2 \frac{1}{2} \text{ lb} \cdot \frac{16 \text{ oz}}{1 \text{ lb}} ~ & \textcolor{red}{ \text{ Multiply by conversion factor.}} \\ = 2 \frac{1}{2} \cancel{ \text{ lb}} \cdot \frac{16 \text{ oz}}{1 \cancel{ \text{ lb}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \left( 2 \frac{1}{2} \cdot 16 \right) \text{ oz } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = \left( \frac{5}{2} \cdot 16 \right) \text{ oz } & \textcolor{red}{ \text{ Mixed to improper fraction.}} \\ = \frac{80}{2} \text{ oz } & \textcolor{red}{ \text{ Multiply.}} \\ = 40 \text{ oz } & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]

De ahí que las$2 \frac{1}{2}$ libras equivalen a 40 onzas.

Ejercicio

Cambia$6 \frac{1}{4}$ libras a onzas.

Contestar: 100 onzas

Ejemplo 7

Cambiar 3.2 toneladas a onzas.

Solución

Este ejercicio requiere multiplicarse por una cadena de factores de conversión.

\[ \begin{aligned} 3.2 \text{ ton } = 3.2 \text{ ton } \cdot \frac{2000 \text{ lb}}{1 \text{ ton}} \cdot \frac{16 \text{ oz}}{1 \text{ lb}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 3.2 \cancel{ \text{ ton}} \cdot \frac{2000 \cancel{ \text{ lb}}}{1 \cancel{ \text{ ton}}} \cdot \frac{16 \text{ oz}}{1 \cancel{ \text{ lb}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{3.2 \cdot 2000 \cdot 16}{1 \cdot 1} \text{ oz } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 102,400 \text{ oz } & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

De ahí que 3.2 toneladas equivalen a 102,400 onzas.

Ejercicio

Cambiar 4.1 toneladas a onzas.

Contestar: 128,000 onzas

Unidades de Volumen

Las unidades de volumen más comunes son onzas líquidas, tazas, pintas, cuartos de galón y galones. Nos enfocaremos en convertir de una unidad a otra.

Unidades Americanas de Volumen

Hechos relativos a unidades comunes de volumen.

1 taza (c) = 8 onzas líquidas (fl oz)
1 pinta (pt) = 2 tazas (c)
1 cuarto (qt) = 2 pintas (pt)
1 galón (gal) = 4 cuartos (qt)

Estos hechos conducen a los factores de conversión enumerados en el Cuadro 6.3.

Cuadro 6.3: Factores de conversión para unidades de volumen.
Convertir	Factor de conversión	Convertir	Factor de conversión
tazas a onzas	8 fl oz/1 C	onzas a tazas	1c/8 fl oz
pintas a tazas	2 c/1 pt	tazas a pintas	1 pt/2 c
cuartos de galón a pintas	2 pt/1 qt	pintas a cuartos	1 qt/2 pt
galones a cuartos	4 qt/1 gal	cuartos a galones	1 gal/4 qt

Ejemplo 8

Cambiar 5.6 galones a pintas.

Solución

Este ejercicio requiere multiplicarse por una cadena de factores de conversión.

\[ \begin{aligned} 5.6 \text{ gal } = 5.6 \text{ gal } \cdot \frac{4 \text{ qt}}{1 \text{ gal}} \cdot \frac{2 \text{ pt}}{1 \text{ qt}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 5.6 \cancel{\text{ gal }} \cdot \frac{4 \cancel{\text{ qt}}}{1 \cancel{ \text{ gal}}} \cdot \frac{2 \text{ pt}}{1 \cancel{ \text{ qt}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{5.6 \cdot 4 \cdot 2}{1 \cdot 1} \text{ pt } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 44.8 \text{ pt } & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

De ahí que 5.6 galones equivalen a 44.8 pintas.

Ejercicio

Cambiar 3.2 galones a pintas.

Contestar: 25.6 pintas

Unidades de Tiempo

Las unidades de tiempo más comunes son segundos, minutos, horas, días y años.

Unidades Americanas del Tiempo

Hechos relativos a unidades comunes de tiempo.

1 minuto (min) = 60 segundo (s)
1 hora (hr) = 60 minutos (min)
1 día (día) = 24 horas (h)
1 año (año) = 365 días (día)

Estos hechos conducen a los factores de conversión en el Cuadro 6.4.

Cuadro 6.4: Factores de conversión para unidades de tiempo.
Convertir	Factor de conversión	Convertir	Factor de conversión
minutos a segundos	60 s/1 min	segundos a minutos	1 min/60 s
horas a minutos	60 min/1 hr	minutos a horas	1 hr/60 min
días a horas	24 hr/1 día	horas a días	1 día/24 hr
años a días	365 día/1 año	días a años	1 año/365 días

Ejemplo 9

¿Cuántos segundos en un año?

Solución

Se necesita una cadena de factores de conversión.

\[ \begin{aligned} 1 \text{ yr } = 1 \text{ yr } \cdot \frac{365 \text{ day}}{1 \text{ yr}} \cdot \frac{24 \text{ hr}}{1 \text{ day}} \cdot \frac{60 \text{ min}}{1 \text{ hr}} \cdot \frac{60 \text{ s}}{1 \text{ min}} ~ & \textcolor{red}{ \text{ Conversion factors.}} \\ = 1 \cancel{ \text{ yr}} \cdot \frac{365 \cancel{ \text{ day}}}{1 \cancel{ \text{ yr}}} \cdot \frac{24 \cancel{ \text{ hr}}}{1 \cancel{ \text{ day}}} \cdot \frac{60 \cancel{ \text{ min}}}{1 \cancel{ \text{ hr}}} \cdot \frac{60 \text{ s}}{1 \cancel{ \text{ min}}} & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{1 \cdot 365 \cdot 24 \cdot 60 \cdot 60}{1 \cdot 1 \cdot 1 \cdot 1} \text{ s } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 31,536,000 \text{ s } & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Así, 1 año equivale a 31,536,000 segundos.

Ejercicio

¿Cuántos segundos en un día?

Contestar: 86,400 segundos

Conversión de Unidades de Velocidad

¿Alguna vez se preguntó qué tan rápido se mueve un beisbol?

Ejemplo 10

Un lanzador profesional puede lanzar una pelota de béisbol a 95 millas por hora. ¿Qué tan rápido es esto en pies por segundo? Redondee su respuesta al pie por segundo más cercano.

Solución

Hay 5280 pies en una milla, 60 minutos en una hora y 60 segundos en un minuto.

\[ \begin{aligned} 95 \frac{ \text{mi}}{ \text{h}} \approx 95 \frac{ \text{mi}}{\text{h}} \cdot \frac{5280 \text{ ft}}{1 \text{ mi}} \cdot \frac{1 \text{ h}}{60 \text{ min}} \cdot \frac{1 \text{ min}}{60 \text{ s}} ~ & \textcolor{red}{ \text{ Conversion factors.}} \\ \approx 95 \frac{ \cancel{\text{mi}}}{\cancel{\text{h}}} \cdot \frac{5280 \text{ ft}}{1 \cancel{\text{ mi}}} \cdot \frac{1 \cancel{\text{ h}}}{60 \cancel{\text{ min}}} \cdot \frac{1 \cancel{\text{ min}}}{60 \text{ s}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ \approx \frac{95 \cdot 5280 \cdot 1 \cdot 1}{1 \cdot 60 \cdot 60} \frac{ \text{ft}}{\text{s}} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ \approx 139.3 \frac{ \text{ft}}{\text{s}} ~ & \textcolor{red}{ \text{ Multiply and divide.}} \end{aligned}\nonumber \]

Para redondear al pie por segundo más cercano, identifique los dígitos de redondeo y pruebe.

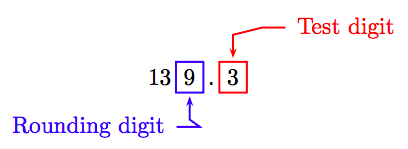
$Screen Shot 2019-09-20 a las 12.42.19 PM.png$

Debido a que el dígito de prueba es menor que 5, deje el dígito de redondeo solo y trunca. Así, al pie por segundo más cercano, la velocidad es de aproximadamente 139 pies por segundo.

¡Uf! Ya que la masa se encuentra en el plato de casa, que está a unos 60 pies de donde se entrega el terreno de juego, ¡la masa tiene menos de 1/2 segundo para reaccionar al terreno de juego!

Ejercicio

Una lanzadora de softbol femenino puede lanzar su bola rápida a 60 millas por hora. ¿Qué tan rápido es esto en pies por segundo? Redondee su respuesta al pie por segundo más cercano.

Contestar: 88 pies por segundo

Ejercicios

1. Cambiar 8 yardas a pies.

2. Cambiar 60 yardas a pies.

3. Cambia 261 pies a yardas.

4. Cambia 126 pies a yardas.

5. Cambia 235 pulgadas a yardas. Redondee su respuesta a la décima de yarda más cercana.

6. Cambia 244 pulgadas a yardas. Redondee su respuesta a la décima de yarda más cercana.

7. Cambia 141 pies a yardas.

8. Cambia 78 pies a yardas.

9. Cambia 2.8 millas a pies.

10. Cambia 4.9 millas a pies.

11. Cambia 104 pulgadas a yardas. Redondee su respuesta a la décima de yarda más cercana.

12. Cambia 101 pulgadas a yardas. Redondee su respuesta a la décima de yarda más cercana.

13. Cambie 168,372 pulgadas a millas, corrija a la décima de milla más cercana.

14. Cambie 198,550 pulgadas a millas, corrija a la décima de milla más cercana.

15. Cambia 82 pies a pulgadas.

16. Cambia 80 pies a pulgadas.

17. Cambia 2.9 yardas a pulgadas. Redondee su respuesta a la pulgada más cercana.

18. Cambia 4.5 yardas a pulgadas. Redondee su respuesta a la pulgada más cercana.

19. Cambia 25,756 pies a millas. Redondee su respuesta a la décima de milla más cercana.

20. Cambia 19,257 pies a millas. Redondee su respuesta a la décima de milla más cercana.

21. Cambia 5 yardas a pies.

22. Cambiar 20 yardas a pies.

23. Cambie 169,312 pulgadas a millas, corrija a la décima de milla más cercana.

24. Cambiar 162,211 pulgadas a millas, corregir a la décima de milla más cercana.

25. Cambia 1.5 yardas a pulgadas. Redondee su respuesta a la pulgada más cercana.

26. Cambia 2.1 yardas a pulgadas. Redondee su respuesta a la pulgada más cercana.

27. Cambia 360 pulgadas a pies.

28. Cambia 768 pulgadas a pies.

29. Cambia 48 pulgadas a pies.

30. Cambia 528 pulgadas a pies.

31. Cambia 15,363 pies a millas. Redondee su respuesta a la décima de milla más cercana.

32. Cambia 8,540 pies a millas. Redondee su respuesta a la décima de milla más cercana.

33. Cambia 1.7 millas a pulgadas.

34. Cambia 4.7 millas a pulgadas.

35. Cambia 3.1 millas a pulgadas.

36. Cambia 1.8 millas a pulgadas.

37. Cambia 3.6 millas a pies.

38. Cambia 3.1 millas a pies.

39. Cambia 18 pies a pulgadas.

40. Cambia 33 pies a pulgadas.

41. Cambia$5 \frac{1}{8}$ libras a onzas.

42. Cambia$3 \frac{1}{16}$ libras a onzas.

43. Cambiar 2.4 toneladas a onzas.

44. Cambiar 3.4 toneladas a onzas.

45. Cambia 34 onzas a libras. Exprese su respuesta como una fracción reducida a los términos más bajos.

46. Cambia 78 onzas a libras. Exprese su respuesta como una fracción reducida a los términos más bajos.

47. Cambiar 2.2 toneladas a libras.

48. Cambiar 4.8 toneladas a libras.

49. Cambia 70 onzas a libras. Exprese su respuesta como una fracción reducida a los términos más bajos.

50. Cambia 20 onzas a libras. Exprese su respuesta como una fracción reducida a los términos más bajos.

51. Cambia 9,560 libras a toneladas. Redondee su respuesta a la décima de tonelada más cercana.

52. Cambia 9,499 libras a toneladas. Redondee su respuesta a la décima de tonelada más cercana.

53. Cambia$2 \frac{1}{2}$ libras a onzas.

54. Cambia$7 \frac{1}{16}$ libras a onzas.

55. Cambiar 5.9 toneladas a libras.

56. Cambiar 2.1 toneladas a libras.

57. Cambiar 2.5 toneladas a onzas.

58. Cambiar 5.3 toneladas a onzas.

59. Cambia 8,111 libras a toneladas. Redondee su respuesta a la décima de tonelada más cercana.

60. Cambia 8,273 libras a toneladas. Redondee su respuesta a la décima de tonelada más cercana.

61. Cambiar 4.5625 pintas a onzas líquidas.

62. Cambiar 2.9375 pintas a onzas líquidas.

63. Cambia 32 onzas líquidas a pintas.

64. Cambia 160 onzas líquidas a pintas.

65. Cambiar 3.7 galones a pintas.

66. Cambiar 2.4 galones a pintas.

67. Cambia 216 pintas a galones.

68. Cambia 96 pintas a galones.

69. Cambia 544 onzas líquidas a pintas.

70. Cambia 432 onzas líquidas a pintas.

71. Cambia 112 pintas a galones.

72. Cambiar 200 pintas a galones.

73. Cambiar 7.7 galones a pintas.

74. Cambiar 5.7 galones a pintas.

75. Cambia 3.875 pintas a onzas líquidas.

76. Cambia 3 pintas a onzas líquidas.

77. Cambiar 7.8 años a horas.

78. Cambiar 4.7 años a horas.

79. Cambiar 7.6 años a horas.

80. Cambiar 6.6 años a horas.

81. Cambiar 4,025,005 segundos a días. Redondee su respuesta al décimo de día más cercano.

82. Cambiar 4,672,133 segundos a días. Redondee su respuesta al décimo de día más cercano.

83. Cambiar 37,668 horas a años.

84. Cambiar 40,296 horas a años.

85. Cambiar 22,776 horas a años.

86. Cambiar 29,784 horas a años.

87. Cambia 96 días a segundos.

88. Cambiar 50 días a segundos.

89. Cambiar 40 días a segundos.

90. Cambiar 10 días a segundos.

91. Cambiar 3,750,580 segundos a días. Redondee su respuesta al décimo de día más cercano.

92. Cambiar 4,493,469 segundos a días. Redondee su respuesta al décimo de día más cercano.

93. Cambia 367 pies por segundo a millas por hora. Redondee su respuesta a la milla por hora más cercana.

94. Cambia 354 pies por segundo a millas por hora. Redondee su respuesta a la milla por hora más cercana.

95. Cambia 442 pies por segundo a millas por hora. Redondee su respuesta a la milla por hora más cercana.

96. Cambia 388 pies por segundo a millas por hora. Redondee su respuesta a la milla por hora más cercana.

97. Cambia 30 millas por hora a pies por segundo. Redondee su respuesta al pie por segundo más cercano.

98. Cambia 99 millas por hora a pies por segundo. Redondee su respuesta al pie por segundo más cercano.

99. Cambia 106 millas por hora a pies por segundo. Redondee su respuesta al pie por segundo más cercano.

100. Cambia 119 millas por hora a pies por segundo. Redondee su respuesta al pie por segundo más cercano.

101. Hombre fuerte. El famoso hombre fuerte Joe Rollino, quien seguía doblando cuartos con los dedos a los 104 años, una vez levantó 3, 200 libras en el Parque de Atracciones Coney Island. ¿Cuántas toneladas levantó Joe ese día? Associated Press-Times-Standard 01/12/10 Parque de diversiones NYC strongman, 104, asesinado por camioneta.

102. Día de la Tierra. La cantidad de tiempo que tarda la Tierra en rotar una vez alrededor de su eje es de un día. ¿Cuántos segundos es eso?

103. Rotura de agua. “La edad promedio de las tuberías de agua de Washington, DC es de 76 años, y no están solas. Cada dos minutos, en algún lugar del país, se rompe una pipa”. ¿Cuántas pipas se rompen cada año en EU? New York Times 14/03/10 Ahorrar los sistemas de agua y alcantarillado de Estados Unidos podría ser costoso.

RESPUESTAS

1. 24 pies

3. 87 yardas

5. 6.5 yardas

7. 47 yardas

9. 14,784 pies

11. 2.9 yardas

13. 2.7 millas

15. 984 pulgadas

17. 104 pulgadas

19. 4.9 millas

21. 15 pies

23. 2.7 millas

25. 54 pulgadas

27. 30 pies

29. 4 pies

31. 2.9 millas

33. 107,712 pulgadas

35. 196,416 pulgadas

37. 19,008 pies

39. 216 pulgadas

41. 82 onzas

43. 76,800 onzas

45. $2 \frac{1}{8}$libras

47. 4,400 libras

49. $4 \frac{3}{8}$libras

51. 4.8 toneladas

53. 40 onzas

55. 11,800 libras

57. 80,000 onzas

59. 4.1 toneladas

61. 73 onzas líquidas

63. 2 pintas

65. 29.6 pintas

67. 27 galones

69. 34 pintas

71. 14 galones

73. 61.6 pintas

75. 62 onzas líquidas

77. 68,328 horas

79. 66,576 horas

81. 46.6 días

83. 4.3 años

85. 2.6 años

87. 8,294,400 segundos

89. 3,456,000 segundos

91. 43.4 días

93. 250 mi/h

95. 301 mi/h

97. 44 pies/s

99. 155 pies/s

101. 1.6 toneladas

103. 262, 800