Inicio
Matemáticas
Pre-Álgebra
Libro: Preálgebra (OpenStax)
4: Fracciones
4.8: Suma y resta fracciones con diferentes denominadores (Parte 1)

4.8: Suma y resta fracciones con diferentes denominadores (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114245

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Encuentra el mínimo denominador común (LCD)
Convertir fracciones a fracciones equivalentes con la pantalla LCD
Sumar y restar fracciones con diferentes denominadores
Identificar y usar operaciones de fracciones
Utilice el orden de las operaciones para simplificar fracciones complejas
Evaluar expresiones variables con fracciones

¡prepárate!

Antes de comenzar, toma este cuestionario de preparación.

Encuentra dos fracciones equivalentes a$\dfrac{5}{6}$. Si te perdiste este problema, revisa el Ejemplo 4.1.14.
Simplificar:$\dfrac{1 + 5 \cdot 3}{2^{2} + 4}$. Si te perdiste este problema, revisa el Ejemplo 4.3.13.

Encuentre el denominador menos común

En el apartado anterior, explicamos cómo sumar y restar fracciones con un denominador común. Pero, ¿cómo podemos sumar y restar fracciones con denominadores distintos?

Pensemos de nuevo en las monedas. ¿Se puede agregar un cuarto y un centavo? Se podría decir que hay dos monedas, pero eso no es muy útil. Para encontrar el valor total de un cuarto más una moneda de diez centavos, los cambias al mismo tipo de unidad: centavos. Un cuarto equivale a$25$ centavos y un centavo equivale a$10$ centavos, por lo que la suma es$35$ centavos. Ver Figura$\PageIndex{1}$.

$Se muestran un cuarto y una moneda de diez centavos. Debajo de ellos, dice 25 centavos más 10 centavos. Debajo de eso, dice 35 centavos.$

Figura$\PageIndex{1}$: Juntos, un cuarto y una moneda de diez centavos valen 35 centavos, o$\dfrac{35}{100}$ de un dólar.

De igual manera, cuando sumamos fracciones con diferentes denominadores tenemos que convertirlas en fracciones equivalentes con un denominador común. Con las monedas, cuando convertimos a centavos, el denominador es$100$. Ya que hay$100$ centavos en un dólar,$25$ centavos es$\dfrac{25}{100}$ y$10$ centavos es$\dfrac{10}{100}$. Entonces agregamos$\dfrac{25}{100} + \dfrac{10}{100}$ para obtener$\dfrac{35}{100}$, que son$35$ centavos.

Has practicado sumar y restar fracciones con denominadores comunes. Ahora veamos qué hay que hacer con fracciones que tienen diferentes denominadores.

Primero, usaremos mosaicos de fracción para modelar encontrando el denominador común de$\dfrac{1}{2}$ y$\dfrac{1}{3}$. Empezaremos con una$\dfrac{1}{2}$ baldosa y una$\dfrac{1}{3}$ baldosa. Queremos encontrar una baldosa de fracción común que podamos usar para que coincida con ambas$\dfrac{1}{2}$ y$\dfrac{1}{3}$ exactamente. Si probamos las$\dfrac{1}{4}$ piezas,$2$ de ellas coinciden exactamente con la$\dfrac{1}{2}$ pieza, pero no coinciden exactamente con la$\dfrac{1}{3}$ pieza.

$Se muestran dos rectángulos uno al lado del otro. El primero está etiquetado como 1 mitad. El segundo es más corto y está etiquetado con 1 tercio. Debajo del primer rectángulo hay un rectángulo de igual tamaño dividido verticalmente en dos piezas, cada una etiquetada con 1 cuarto. Debajo del segundo rectángulo hay dos piezas, cada una etiquetada 1 cuarta. Estos rectángulos juntos son más largos que el rectángulo etiquetado como 1 tercio.$

Figura$\PageIndex{2}$

Si probamos las$\dfrac{1}{5}$ piezas, no cubren exactamente la$\dfrac{1}{2}$ pieza ni la$\dfrac{1}{3}$ pieza.

$Se muestran dos rectángulos uno al lado del otro. El primero está etiquetado como 1 mitad. El segundo es más corto y está etiquetado con 1 tercio. Debajo del primer rectángulo hay tres rectángulos más pequeños, cada uno etiquetado como 1 quinto. Juntos, estos rectángulos son más largos que el medio rectángulo 1. Debajo del rectángulo de 1 tercio hay dos rectángulos más pequeños, cada uno etiquetado como 1 quinto. Juntos, estos rectángulos son más largos que el rectángulo de 1 tercio.$

Figura$\PageIndex{3}$

Si tuviéramos que probar las$\dfrac{1}{12}$ piezas, también funcionarían.

$Se muestran dos rectángulos uno al lado del otro. El primero está etiquetado como 1 mitad. El segundo es más corto y está etiquetado con 1 tercio. Debajo del primer rectángulo hay un rectángulo de igual tamaño dividido verticalmente en 6 piezas, cada una etiquetada 1 duodécima. Debajo del segundo rectángulo hay un rectángulo de igual tamaño dividido verticalmente en 4 piezas, cada una etiquetada 1 duodécima.$

Figura$\PageIndex{4}$

Incluso las baldosas más pequeñas, como$\dfrac{1}{24}$ y$\dfrac{1}{48}$, también cubrirían exactamente la$\dfrac{1}{2}$ pieza y la$\dfrac{1}{3}$ pieza. El denominador de la pieza más grande que cubre ambas fracciones es el mínimo denominador común (LCD) de las dos fracciones. Entonces, el mínimo común denominador de$\dfrac{1}{2}$ y$\dfrac{1}{3}$ es$6$.

Observe que todas las baldosas que cubren$\dfrac{1}{2}$ y$\dfrac{1}{3}$ tienen algo en común: Sus denominadores son múltiplos comunes de$2$ y$3$, los denominadores de$\dfrac{1}{2}$ y$\dfrac{1}{3}$. El mínimo común múltiplo (LCM) de los denominadores es$6$, y así decimos que$6$ es el mínimo común denominador (LCD) de las fracciones$\dfrac{1}{2}$ y$\dfrac{1}{3}$.

Definición: Mínimo denominador común

El mínimo común denominador (LCD) de dos fracciones es el mínimo común múltiplo (LCM) de sus denominadores.

Para encontrar el LCD de dos fracciones, encontraremos el LCM de sus denominadores. Seguimos el procedimiento que utilizamos anteriormente para encontrar el LCM de dos números. Solo usamos los denominadores de las fracciones, no los numeradores, al encontrar la LCD.

Ejemplo$\PageIndex{1}$: lcd

Encuentra la pantalla LCD para las fracciones$\dfrac{7}{12}$ y$\dfrac{5}{18}$.

Solución

Factorizar cada denominador en sus primos.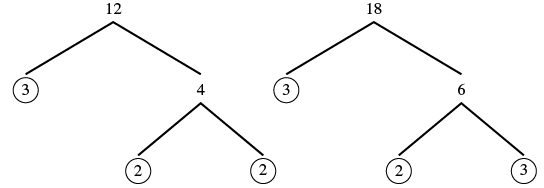
Enumere los primos de 12 y los primos de 18 alineándolos en columnas cuando sea posible.
Derriba las columnas.
Multiplicar los factores. El producto es el LCM.	LCM = 36
El LCM de 12 y 18 es 36, por lo que el LCD de$\dfrac{7}{12}$ y$\dfrac{5}{18}$ es 36.	LCD de$\dfrac{7}{12}$ y$\dfrac{5}{18}$ es 36.

Ejercicio$\PageIndex{1}$

Encuentra el mínimo denominador común para las fracciones:$\dfrac{7}{12}$ y$\dfrac{11}{15}$.

Contestar: $60$

Ejercicio$\PageIndex{2}$

Encuentra el mínimo denominador común para las fracciones:$\dfrac{13}{15}$ y$\dfrac{17}{5}$.

Contestar: $15$

Para encontrar el LCD de dos fracciones, encuentra el LCM de sus denominadores. Observe cómo los pasos que se muestran a continuación son similares a los pasos que tomamos para encontrar el LCM.

CÓMO: ENCONTRAR EL MENOS COMÚN DENIMINADOR (LCD) DE

Paso 1. Factorizar cada denominador en sus primos.

Paso 2. Enumere los primos, coincidiendo los primos en columnas cuando sea posible.

Paso 3. Derriba las columnas.

Paso 4. Multiplicar los factores. El producto es el LCM de los denominadores.

Paso 5. El LCM de los denominadores es el LCD de las fracciones.

Ejemplo$\PageIndex{2}$:

Encuentra el mínimo denominador común para las fracciones$\dfrac{8}{15}$ y$\dfrac{11}{24}$.

Solución

Para encontrar el LCD, encontramos el LCM de los denominadores. Encuentra el LCM de$15$ y$24$.

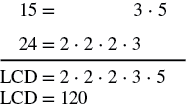
$La línea superior muestra 15 es igual a 3 veces 5. La siguiente línea muestra 24 es igual a 2 veces 2 veces 2 veces 3. Los 3s están alineados verticalmente. La siguiente línea muestra LCM es igual a 2 veces 2 veces 2 veces 3 veces 5. La última línea muestra LCM es igual a 120.$

El LCM de$15$ y$24$ es$120$. Entonces, el LCD de$\dfrac{8}{15}$ y$\dfrac{11}{24}$ es$120$.

Ejercicio$\PageIndex{3}$

Encuentra el mínimo denominador común para las fracciones:$\dfrac{13}{24}$ y$\dfrac{17}{32}$.

Contestar: $96$

Ejercicio$\PageIndex{4}$

Encuentra el mínimo denominador común para las fracciones:$\dfrac{9}{28}$ y$\dfrac{21}{32}$.

Contestar: $224$

Convertir fracciones a fracciones equivalentes con la pantalla LCD

Anteriormente, utilizamos fichas de fracción para ver que la pantalla LCD de$\dfrac{1}{4}$ y$\dfrac{1}{6}$ es$12$. Vimos que tres$\dfrac{1}{12}$ piezas cubiertas exactamente$\dfrac{1}{4}$ y dos$\dfrac{1}{12}$ piezas exactamente cubiertas$\dfrac{1}{6}$, así que

\[\dfrac{1}{4} = \dfrac{3}{12} \quad and \quad \dfrac{1}{6} = \dfrac{2}{12} \ldotp \nonumber \]

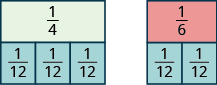
$A la izquierda hay un rectángulo etiquetado con 1 cuarto. Debajo hay un rectángulo idéntico dividido verticalmente en 3 piezas iguales, cada una etiquetada 1 doceava. A la derecha hay un rectángulo etiquetado 1 sexto. Debajo hay un rectángulo idéntico dividido verticalmente en 2 piezas iguales, cada una etiquetada 1 doceava.$

Decimos eso$\dfrac{1}{4}$ y$\dfrac{3}{12}$ son fracciones equivalentes y también eso$\dfrac{1}{6}$ y$\dfrac{2}{12}$ son fracciones equivalentes.

Podemos usar la Propiedad de Fracciones Equivalentes para cambiar algebraicamente una fracción a una equivalente. Recuerde, dos fracciones son equivalentes si tienen el mismo valor. La Propiedad de Fracciones Equivalentes se repite a continuación para referencia.

Definición: Propiedad de Fracciones Equivalentes

Si$a, b, c$ son números enteros donde$b ≠ 0$,$c ≠ 0$, entonces

\[\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c} \quad and \quad \dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}\]

Para sumar o restar fracciones con diferentes denominadores, primero tendremos que convertir cada fracción a una fracción equivalente con la LCD. Veamos cómo cambiar$\dfrac{1}{4}$ y$\dfrac{1}{6}$ a fracciones equivalentes con denominador$12$ sin usar modelos.

Ejemplo$\PageIndex{3}$: conversion

Convertir$\dfrac{1}{4}$ y$\dfrac{1}{6}$ a fracciones equivalentes con denominador$12$, su LCD.

Solución

Encuentra la pantalla LCD.	El LCD de$\dfrac{1}{4}$ y$\dfrac{1}{6}$ es 12.
Encuentra el número para multiplicar 4 para obtener 12.	$4 \cdot \textcolor{red}{3} = 12$
Encuentra el número para multiplicar 6 para obtener 12.	$6 \cdot \textcolor{red}{2} = 12$
Utilice la Propiedad de Fracciones Equivalentes para convertir cada fracción en una fracción equivalente con la LCD, multiplicando tanto el numerador como el denominador de cada fracción por el mismo número.	$\begin{split} \dfrac{1}{4} \qquad & \dfrac{1}{6} \\ \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} \qquad & \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} \end{split}$
Simplificar los numeradores y denominadores.	$\dfrac{3}{12} \qquad \dfrac{2}{12}$

No reducimos las fracciones resultantes. Si lo hiciéramos, volveríamos a nuestras fracciones originales y perderíamos el denominador común.

Ejercicio$\PageIndex{5}$

Cambiar a fracciones equivalentes con la pantalla LCD:$\dfrac{3}{4}$ y$\dfrac{5}{6}$,$LCD = 12$

Contestar: $\dfrac{9}{12}, \dfrac{10}{12}$

Ejercicio$\PageIndex{6}$

Cambiar a fracciones equivalentes con la pantalla LCD:$- \dfrac{7}{12}$ y$\dfrac{11}{15}$,$LCD = 60$

Contestar: $-\dfrac{35}{60}, \dfrac{44}{60}$

CÓMO: CONVERTIR DOS FRACCIONES EN FRACCIONES EQUIVALES CON SU LCD COMO denominador

Paso 1. Encuentra la pantalla LCD.

Paso 2. Para cada fracción, determine el número necesario para multiplicar el denominador para obtener la LCD.

Paso 3. Usa la Propiedad Fracciones Equivalentes para multiplicar tanto el numerador como el denominador por el número que encontraste en el Paso 2.

Paso 4. Simplifica el numerador y denominador.

Ejemplo$\PageIndex{4}$: conversion

Convertir$\dfrac{8}{15}$ y$\dfrac{11}{24}$ a fracciones equivalentes con denominador$120$, su LCD.

Encuentra el número que debe multiplicar 15 para obtener 120.	$15 \cdot \textcolor{red}{8} = 120$
Encuentra el número que debe multiplicar 24 para obtener 120.	$24 \cdot \textcolor{red}{5} = 120$
Utilice la Propiedad Fracciones Equivalentes.	$\dfrac{8 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} \qquad \dfrac{11 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}$
Simplificar los numeradores y denominadores.	$\dfrac{64}{120} \qquad \dfrac{55}{120}$

Ejercicio$\PageIndex{7}$

Cambiar a fracciones equivalentes con la pantalla LCD:$\dfrac{13}{24}$ y$\dfrac{17}{32}$, LCD$96$

Contestar: $\dfrac{52}{96}, \dfrac{51}{96}$

Ejercicio$\PageIndex{8}$

Cambiar a fracciones equivalentes con la pantalla LCD:$\dfrac{9}{28}$ y$\dfrac{27}{32}$, LCD$224$

Contestar: $\dfrac{72}{224}, \dfrac{189}{224}$

Sumar y restar fracciones con diferentes denominadores

Una vez convertidos dos fracciones a formas equivalentes con denominadores comunes, podemos sumarlas o restarlas sumando o restando los numeradores.

CÓMO: SUMAR O RESTAR FRACCIONES CON DIFERENTES DENOMIN

Paso 1. Encuentra la pantalla LCD.

Paso 2. Convierte cada fracción a una forma equivalente con la LCD como denominador.

Paso 3. Sumar o restar las fracciones.

Paso 4. Escribe el resultado en forma simplificada.

Ejemplo$\PageIndex{5}$: add

Agregar:$\dfrac{1}{2} + \dfrac{1}{3}$.

Solución

Encuentra la pantalla LCD de 2, 3.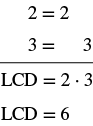
Cambia a fracciones equivalentes con la LCD 6.	$\dfrac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}$
Simplificar los numeradores y denominadores.	$\dfrac{3}{6} + \dfrac{2}{6}$
Agregar.	$\dfrac{5}{6}$

Recuerda, comprueba siempre para ver si se puede simplificar la respuesta. Dado que$5$ y no$6$ tienen factores comunes, la fracción$\dfrac{5}{6}$ no se puede reducir.

Ejercicio$\PageIndex{9}$

Agregar:$\dfrac{1}{4} + \dfrac{1}{3}$.

Contestar: $\dfrac{7}{12}$

Ejercicio$\PageIndex{10}$

Agregar:$\dfrac{1}{2} + \dfrac{1}{5}$.

Contestar: $\dfrac{7}{10}$

Ejemplo$\PageIndex{6}$: subtract

Restar:$\dfrac{1}{2} - \left(- \dfrac{1}{4}\right)$.

Solución

Encuentra la pantalla LCD de 2 y 4.
Reescribe como fracciones equivalentes usando la pantalla LCD 4.	$\dfrac{1 \cdot \textcolor{red}{2}}{2 \cdot \textcolor{red}{2}} - \left(- \dfrac{1}{4}\right)$
Simplifica la primera fracción.	$\dfrac{2}{4} - \left(- \dfrac{1}{4}\right)$
Restar.	$\dfrac{2 - (-1)}{4}$
Simplificar.	$\dfrac{3}{4}$

Una de las fracciones ya tenía el mínimo denominador común, así que sólo tuvimos que convertir la otra fracción.

Ejercicio$\PageIndex{11}$

Restar:$\dfrac{1}{2} - \left(- \dfrac{1}{8}\right)$.

Contestar: $\dfrac{5}{8}$

Ejercicio$\PageIndex{12}$

Restar:$\dfrac{1}{3} - \left(- \dfrac{1}{6}\right)$.

Contestar: $\dfrac{1}{2}$

Ejemplo$\PageIndex{7}$: add

Agregar:$\dfrac{7}{12} + \dfrac{5}{18}$.

Solución

Encuentra la pantalla LCD de 12 y 18.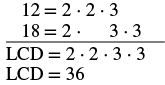
Reescribe como fracciones equivalentes con la pantalla LCD.	$\dfrac{7 \cdot \textcolor{red}{3}}{12 \cdot \textcolor{red}{3}} + \dfrac{5 \cdot \textcolor{red}{2}}{18 \cdot \textcolor{red}{2}}$
Simplificar los numeradores y denominadores.	$\dfrac{21}{36} + \dfrac{10}{36}$
Agregar.	$\dfrac{31}{36}$

Debido a que$31$ es un número primo, no tiene factores en común con$36$. La respuesta se simplifica.

Ejercicio$\PageIndex{13}$

Agregar:$\dfrac{7}{12} + \dfrac{11}{15}$.

Contestar: $\dfrac{79}{60}$

Ejercicio$\PageIndex{14}$

Agregar:$\dfrac{13}{15} + \dfrac{17}{20}$.

Contestar: $\dfrac{103}{60}$

Cuando usamos la Propiedad de Fracciones Equivalentes, hay una manera rápida de encontrar el número por el que necesitas multiplicar para obtener la LCD. Escribe los factores de los denominadores y el LCD tal como lo hiciste para encontrar el LCD. Los factores “faltantes” de cada denominador son los números que necesitas.

$La primera línea dice 12 es igual a 2 veces 2 por 3. Hay un espacio en blanco al lado del 3. La siguiente línea dice 18 es igual a 2 veces 3 por 3. Hay un espacio en blanco entre el 2 y el primero 3. Hay líneas rojas dibujadas a partir de los espacios en blanco. Esto está etiquetado como factores faltantes. Hay una línea horizontal. Por debajo de la línea, dice LCD es igual a 2 veces 2 veces 3 veces 3. Debajo de esto, dice LCD equivale a 36.$

El LCD,$36$, tiene$2$ factores de$2$ y$2$ factores de$3$. Doce tiene dos factores de$2$, pero sólo uno de$3$ —por lo que le 'falta' uno$3$. Multiplicamos el numerador y denominador de$\dfrac{7}{12}$ por$3$ para obtener una fracción equivalente con denominador$36$. A dieciocho le falta un factor de$2$ —entonces multiplicas el numerador y el denominador$\dfrac{5}{18}$ por$2$ para obtener una fracción equivalente con denominador$36$. Aplicaremos este método a medida que restemos las fracciones en el siguiente ejemplo.

Ejemplo$\PageIndex{8}$: subtract

Restar:$\dfrac{7}{15} − \dfrac{19}{24}$.

Solución

Encuentra la pantalla LCD. 15 está 'faltando' tres factores de 2 24 es 'faltante' un factor de 5
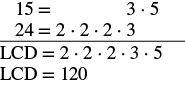Reescribe como fracciones equivalentes con la pantalla LCD.	$\dfrac{7 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} - \dfrac{19 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}$
Simplifica cada numerador y denominador.	$\dfrac{56}{120} - \dfrac{95}{120}$
Restar.	$- \dfrac{39}{120}$
Reescribir mostrando el factor común de 3.	$- \dfrac{13 \cdot 3}{40 \cdot 3}$
Eliminar el factor común para simplificar.	$- \dfrac{13}{40}$

Ejercicio$\PageIndex{15}$

Restar:$\dfrac{13}{24} − \dfrac{17}{32}$.

Contestar: $\dfrac{1}{96}$

Ejercicio$\PageIndex{16}$

Restar:$\dfrac{21}{32} − \dfrac{9}{28}$.

Contestar: $\dfrac{75}{224}$

Ejemplo$\PageIndex{9}$: add

Agregar:$- \dfrac{11}{30} + \dfrac{23}{42}$.

Solución

Encuentra la pantalla LCD.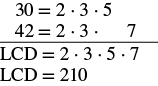
Reescribe como fracciones equivalentes con la pantalla LCD.	$- \dfrac{11 \cdot \textcolor{red}{7}}{30 \cdot \textcolor{red}{7}} + \dfrac{23 \cdot \textcolor{red}{5}}{42 \cdot \textcolor{red}{5}}$
Simplifica cada numerador y denominador.	$- \dfrac{77}{210} + \dfrac{115}{210}$
Agregar.	$\dfrac{38}{210}$
Reescribir mostrando el factor común de 2.	$\dfrac{19 \cdot 2}{105 \cdot 2}$
Eliminar el factor común para simplificar.	$\dfrac{19}{105}$

Ejercicio$\PageIndex{17}$

Agregar:$- \dfrac{13}{42} + \dfrac{17}{35}$.

Contestar: $\dfrac{37}{210}$

Ejercicio$\PageIndex{18}$

Agregar:$- \dfrac{19}{24} + \dfrac{17}{32}$.

Contestar: $-\dfrac{25}{96}$

En el siguiente ejemplo, una de las fracciones tiene una variable en su numerador. Seguimos los mismos pasos que cuando ambos numeradores son números.

Ejemplo$\PageIndex{10}$: add

Agregar:$\dfrac{3}{5} + \dfrac{x}{8}$.

Solución

Las fracciones tienen diferentes denominadores.

Encuentra la pantalla LCD.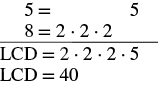
Reescribe como fracciones equivalentes con la pantalla LCD.	$\dfrac{3 \cdot \textcolor{red}{8}}{5 \cdot \textcolor{red}{8}} + \dfrac{x \cdot \textcolor{red}{5}}{8 \cdot \textcolor{red}{5}}$
Simplificar los numeradores y denominadores.	$\dfrac{24}{40} + \dfrac{5x}{40}$
Agregar.	$\dfrac{24 + 5x}{40}$

No podemos añadir$24$ y$5x$ ya que no son como términos, por lo que no podemos simplificar más la expresión.

Ejercicio$\PageIndex{19}$

Agregar:$\dfrac{y}{6} + \dfrac{7}{9}$.

Contestar: $\dfrac{3y+14}{18}$

Ejercicio$\PageIndex{20}$

Agregar:$\dfrac{x}{6} + \dfrac{7}{15}$.

Contestar: $\dfrac{5x+14}{30}$

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

Search

Definición: Mínimo denominador común

Ejemplo\(\PageIndex{1}\): lcd

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

CÓMO: ENCONTRAR EL MENOS COMÚN DENIMINADOR (LCD) DE

Ejemplo\(\PageIndex{2}\):

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Definición: Propiedad de Fracciones Equivalentes

Ejemplo\(\PageIndex{3}\): conversion

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

CÓMO: CONVERTIR DOS FRACCIONES EN FRACCIONES EQUIVALES CON SU LCD COMO denominador

Ejemplo\(\PageIndex{4}\): conversion

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

CÓMO: SUMAR O RESTAR FRACCIONES CON DIFERENTES DENOMIN

Ejemplo\(\PageIndex{5}\): add

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejemplo\(\PageIndex{6}\): subtract

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejemplo\(\PageIndex{7}\): add

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejemplo\(\PageIndex{8}\): subtract

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejemplo\(\PageIndex{9}\): add

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejemplo\(\PageIndex{10}\): add

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Encuentra la pantalla LCD.	El LCD de\(\dfrac{1}{4}\) y\(\dfrac{1}{6}\) es 12.
Encuentra el número para multiplicar 4 para obtener 12.	\(4 \cdot \textcolor{red}{3} = 12\)
Encuentra el número para multiplicar 6 para obtener 12.	\(6 \cdot \textcolor{red}{2} = 12\)
Utilice la Propiedad de Fracciones Equivalentes para convertir cada fracción en una fracción equivalente con la LCD, multiplicando tanto el numerador como el denominador de cada fracción por el mismo número.	\(\begin{split} \dfrac{1}{4} \qquad & \dfrac{1}{6} \\ \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} \qquad & \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} \end{split}\)
Simplificar los numeradores y denominadores.	\(\dfrac{3}{12} \qquad \dfrac{2}{12}\)

Encuentra el número que debe multiplicar 15 para obtener 120.	\(15 \cdot \textcolor{red}{8} = 120\)
Encuentra el número que debe multiplicar 24 para obtener 120.	\(24 \cdot \textcolor{red}{5} = 120\)
Utilice la Propiedad Fracciones Equivalentes.	\(\dfrac{8 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} \qquad \dfrac{11 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}\)
Simplificar los numeradores y denominadores.	\(\dfrac{64}{120} \qquad \dfrac{55}{120}\)

Encuentra la pantalla LCD de 2, 3.
Cambia a fracciones equivalentes con la LCD 6.	\(\dfrac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}\)
Simplificar los numeradores y denominadores.	\(\dfrac{3}{6} + \dfrac{2}{6}\)
Agregar.	\(\dfrac{5}{6}\)

Encuentra la pantalla LCD de 2 y 4.
Reescribe como fracciones equivalentes usando la pantalla LCD 4.	\(\dfrac{1 \cdot \textcolor{red}{2}}{2 \cdot \textcolor{red}{2}} - \left(- \dfrac{1}{4}\right)\)
Simplifica la primera fracción.	\(\dfrac{2}{4} - \left(- \dfrac{1}{4}\right)\)
Restar.	\(\dfrac{2 - (-1)}{4}\)
Simplificar.	\(\dfrac{3}{4}\)

Encuentra la pantalla LCD de 12 y 18.
Reescribe como fracciones equivalentes con la pantalla LCD.	\(\dfrac{7 \cdot \textcolor{red}{3}}{12 \cdot \textcolor{red}{3}} + \dfrac{5 \cdot \textcolor{red}{2}}{18 \cdot \textcolor{red}{2}}\)
Simplificar los numeradores y denominadores.	\(\dfrac{21}{36} + \dfrac{10}{36}\)
Agregar.	\(\dfrac{31}{36}\)

Encuentra la pantalla LCD. 15 está 'faltando' tres factores de 2 24 es 'faltante' un factor de 5
Reescribe como fracciones equivalentes con la pantalla LCD.	\(\dfrac{7 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} - \dfrac{19 \cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}\)
Simplifica cada numerador y denominador.	\(\dfrac{56}{120} - \dfrac{95}{120}\)
Restar.	\(- \dfrac{39}{120}\)
Reescribir mostrando el factor común de 3.	\(- \dfrac{13 \cdot 3}{40 \cdot 3}\)
Eliminar el factor común para simplificar.	\(- \dfrac{13}{40}\)

Encuentra la pantalla LCD.
Reescribe como fracciones equivalentes con la pantalla LCD.	\(- \dfrac{11 \cdot \textcolor{red}{7}}{30 \cdot \textcolor{red}{7}} + \dfrac{23 \cdot \textcolor{red}{5}}{42 \cdot \textcolor{red}{5}}\)
Simplifica cada numerador y denominador.	\(- \dfrac{77}{210} + \dfrac{115}{210}\)
Agregar.	\(\dfrac{38}{210}\)
Reescribir mostrando el factor común de 2.	\(\dfrac{19 \cdot 2}{105 \cdot 2}\)
Eliminar el factor común para simplificar.	\(\dfrac{19}{105}\)

Encuentra la pantalla LCD.
Reescribe como fracciones equivalentes con la pantalla LCD.	\(\dfrac{3 \cdot \textcolor{red}{8}}{5 \cdot \textcolor{red}{8}} + \dfrac{x \cdot \textcolor{red}{5}}{8 \cdot \textcolor{red}{5}}\)
Simplificar los numeradores y denominadores.	\(\dfrac{24}{40} + \dfrac{5x}{40}\)
Agregar.	\(\dfrac{24 + 5x}{40}\)