Saltar al contenido principal
LibreTexts Español

5.12: Simplificar y Usar Raíces Cuadradas (Parte 1)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114294

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Simplifica expresiones con raíces cuadradas
    • Estimar raíces cuadradas
    • Raíces cuadradas aproximadas
    • Simplifique las expresiones variables con raíces cuadradas
    • Uso de raíces cuadradas en aplicaciones
    ¡prepárate!

    Antes de comenzar, toma este cuestionario de preparación.

    1. Simplificar: (−9) 2. Si te perdiste este problema, revisa el Ejemplo 3.7.6.
    2. Vuelta 3.846 a la centésima más cercana. Si te perdiste este problema, revisa el Ejemplo 5.2.9.
    3. Evalúa 12d para d = 80. Si te perdiste este problema, revisa el Ejemplo 2.3.2.

    Simplifique las expresiones con raíces cuadradas

    Para iniciar esta sección, necesitamos revisar algunos vocabulario y notación importantes. Recuerda que cuando un número n se multiplica por sí mismo, podemos escribir esto como n 2, que leemos en voz alta como “n al cuadrado”. Por ejemplo, 8 2 se lee como “8 al cuadrado”. Llamamos al 64 el cuadrado de 8 porque 8 2 = 64. De igual manera, 121 es el cuadrado de 11, porque 11 2 = 121.

    Definición: cuadrado de un número

    Si n 2 = m, entonces m es el cuadrado de n.

    Modelado de Cuadros

    ¿Sabes por qué usamos la palabra cuadrado? Si construimos un cuadrado con tres mosaicos en cada lado, el número total de mosaicos sería nueve.

    Se muestra un cuadrado con 3 baldosas en cada lado. Hay un total de 9 azulejos en la plaza.

    Es por ello que decimos que la plaza de tres es de nueve.

    \[3^{2} = 9\]

    Al número 9 se le llama un cuadrado perfecto porque es el cuadrado de un número entero.

    El gráfico muestra los cuadrados de los números de conteo del 1 al 15. Puedes referirte a él para ayudarte a identificar los cuadrados perfectos.

    Se muestra una tabla con dos columnas. La primera columna está etiquetada como “Número” y tiene los valores: n, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 y 15. La segunda columna está etiquetada como “Cuadrado” y tiene los valores: n al cuadrado, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 y 225.

    Definición: cuadrados perfectos

    Un cuadrado perfecto es el cuadrado de un número entero.

    ¿Qué pasa cuando cuadras un número negativo?

    \[\begin{split} (-8)^{2} & = (-8) (-8) \\ & = 64 \end{split}\]

    Cuando multiplicamos dos números negativos, el producto siempre es positivo. Entonces, el cuadrado de un número negativo siempre es positivo. El gráfico muestra los cuadrados de los enteros negativos de −1 a −15.

    Se muestra una tabla con 2 columnas. La primera columna está etiquetada como “Número” y contiene los valores: n, negativo 1, negativo 2, negativo 3, negativo 4, negativo 5, negativo 6, negativo 7, negativo 8, negativo 9, negativo 10, negativo 11, negativo 12, negativo 13, negativo 14 y negativo 15. La siguiente columna está etiquetada como “Cuadrado” y contiene los valores: n al cuadrado, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 y 225.

    ¿Se dio cuenta de que estos cuadrados son los mismos que los cuadrados de los números positivos?

    Raíces Cuadradas

    A veces tendremos que mirar a la inversa la relación entre los números y sus cuadrados. Porque 10 2 = 100, decimos 100 es el cuadrado de 10. También podemos decir que 10 es una raíz cuadrada de 100.

    Definición: Raíz cuadrada de un número

    Un número cuyo cuadrado es m se llama raíz cuadrada de m. Si n 2 = m, entonces n es una raíz cuadrada de m.

    Observe (−10) 2 = 100 también, por lo que −10 también es una raíz cuadrada de 100. Por lo tanto, tanto 10 como −10 son raíces cuadradas de 100. Entonces, cada número positivo tiene dos raíces cuadradas: una positiva y otra negativa.

    ¿Y si solo queremos la raíz cuadrada positiva de un número positivo? El signo radical,\(\sqrt{\quad}\), representa la raíz cuadrada positiva. La raíz cuadrada positiva también se llama raíz cuadrada principal.

    Definición: Notación de raíz cuadrada

    \(\sqrt{m}\)se lee como “la raíz cuadrada de m.” Si m = n 2, entonces m = n para n ≥ 0.

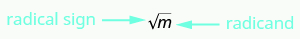
    Se muestra una imagen de una m dentro de un letrero de raíz cuadrada. El signo se etiqueta como un signo radical y la m se etiqueta como el radicando.

    También podemos usar el signo radical para la raíz cuadrada de cero. Porque 0 2 = 0,\(\sqrt{0}\) = 0. Observe que cero tiene solo una raíz cuadrada. El gráfico muestra las raíces cuadradas de los primeros 15 números cuadrados perfectos.

    Se muestra una tabla con 2 columnas. La primera columna contiene los valores: raíz cuadrada de 1, raíz cuadrada de 4, raíz cuadrada de 9, raíz cuadrada de 16, raíz cuadrada de 25, raíz cuadrada de 36, raíz cuadrada de 49, raíz cuadrada de 64, raíz cuadrada de 81, raíz cuadrada de 100, raíz cuadrada de 121, raíz cuadrada de 144, raíz cuadrada de 169, raíz cuadrada de 196, y raíz cuadrada de 225. La segunda columna contiene los valores: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 y 15.

    Ejemplo\(\PageIndex{1}\):

    Simplificar: a)\(\sqrt{25}\) b)\(\sqrt{121}\).

    Solución

    (a)\(\sqrt{25}\)

    Desde 5 2 = 25 5

    b)\(\sqrt{121}\)

    Desde 11 2 = 121 11
    Ejercicio\(\PageIndex{1}\):

    Simplificar: a)\(\sqrt{36}\) b)\(\sqrt{169}\).

    Contestar a

    6

    Respuesta b

    13

    Ejercicio\(\PageIndex{2}\):

    Simplificar: a)\(\sqrt{16}\) b)\(\sqrt{196}\).

    Contestar a

    4

    Respuesta b

    14

    Cada número positivo tiene dos raíces cuadradas y el signo radical indica el positivo. Escribimos\(\sqrt{100}\) = 10. Si queremos encontrar la raíz cuadrada negativa de un número, colocamos un negativo frente al signo radical. Por ejemplo,\(− \sqrt{100}\) = −10.

    Ejemplo\(\PageIndex{2}\):

    Simplificar. a)\(- \sqrt{9}\) b)\(- \sqrt{144}\).

    Solución

    (a)\(- \sqrt{9}\)

    El negativo está frente al signo radical. -3

    b)\(- \sqrt{144}\)

    El negativo está frente al signo radical. -12
    Ejercicio\(\PageIndex{3}\):

    Simplificar: a)\(- \sqrt{4}\) b)\(- \sqrt{225}\).

    Contestar a

    -2

    Respuesta b

    -15

    Ejercicio\(\PageIndex{4}\):

    Simplificar: a)\(- \sqrt{81}\) b)\(- \sqrt{64}\).

    Contestar a

    -9

    Respuesta b

    -8

    Raíz cuadrada de un número negativo

    ¿Podemos simplificar\(\sqrt{−25}\)? ¿Hay un número cuyo cuadrado es −25?

    \[(\;)^{2} = -25?\]

    Ninguno de los números que hemos tratado hasta ahora tiene un cuadrado que sea −25. ¿Por qué? Cualquier número positivo al cuadrado es positivo, y cualquier número negativo al cuadrado también es positivo. En el siguiente capítulo veremos que todos los números con los que trabajamos se llaman los números reales. Entonces decimos que no hay un número real igual a\(\sqrt{−25}\). Si se nos pide encontrar la raíz cuadrada de cualquier número negativo, decimos que la solución no es un número real.

    Ejemplo\(\PageIndex{3}\):

    Simplificar: a)\(\sqrt{−169}\) b)\(− \sqrt{121}\).

    Solución

    (a) No hay un número real cuyo cuadrado sea −169. Por lo tanto, no\(\sqrt{−169}\) es un número real.

    (b) El negativo se encuentra frente al signo radical, por lo que encontramos lo opuesto a la raíz cuadrada de 121.

    El negativo está frente al radical. -11
    Ejercicio\(\PageIndex{5}\):

    Simplificar: a)\(\sqrt{-196}\) b)\(- \sqrt{81}\).

    Contestar a

    no es un número real

    Respuesta b

    -9

    Ejercicio\(\PageIndex{6}\):

    Simplificar: a)\(- \sqrt{49}\) b)\(\sqrt{-121}\).

    Contestar a

    -7

    Respuesta b

    no es un número real

    Las raíces cuadradas y el orden de operaciones

    Al utilizar el orden de las operaciones para simplificar una expresión que tiene raíces cuadradas, tratamos el signo radical como un símbolo de agrupación. Simplificamos cualquier expresión bajo el signo radical antes de realizar otras operaciones.

    Ejemplo\(\PageIndex{4}\):

    Simplificar: a)\(\sqrt{25} + \sqrt{144}\) b)\(\sqrt{25 + 144}\).

    Solución

    (a)

    Utilizar el orden de las operaciones. $$\ sqrt {25} +\ sqrt {144} $$
    Simplifica cada radical. 5 + 12
    Agregar. 17

    b)

    Utilizar el orden de las operaciones. $$\ sqrt {25 + 144} $$
    Añadir bajo el signo radical. $$\ sqrt {169} $$
    Simplificar. 13
    Ejercicio\(\PageIndex{7}\):

    Simplificar: a)\(\sqrt{9} + \sqrt{16}\) b)\(\sqrt{9 + 16}\).

    Contestar a

    7

    Respuesta b

    5

    Ejercicio\(\PageIndex{8}\):

    Simplificar: a)\(\sqrt{64 + 225}\) b)\(\sqrt{64} + \sqrt{225}\).

    Contestar a

    17

    Respuesta b

    23

    Observe las diferentes respuestas en las partes (a) y (b) del Ejemplo\(\PageIndex{4}\). Es importante seguir correctamente el orden de las operaciones. En (a), primero tomamos cada raíz cuadrada y luego las agregamos. En (b), agregamos primero bajo el signo radical y luego encontramos la raíz cuadrada.

    Estimar raíces cuadradas

    Hasta el momento sólo hemos trabajado con raíces cuadradas de cuadrados perfectos. Las raíces cuadradas de otros números no son números enteros.

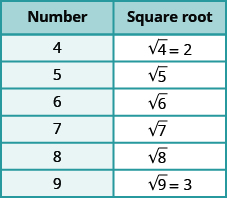
    Se muestra una tabla con 2 columnas. La primera columna está etiquetada como “Número” y contiene los valores: 4, 5, 6, 7, 8, 9. La segunda columna está etiquetada como “Raíz cuadrada” y contiene los valores: raíz cuadrada de 4 es igual a 2, raíz cuadrada de 5, raíz cuadrada de 6, raíz cuadrada de 7, raíz cuadrada de 8, raíz cuadrada de 9 es igual a 3.

    Podríamos concluir que las raíces cuadradas de los números entre 4 y 9 estarán entre 2 y 3, y no serán números enteros. Con base en el patrón de la tabla anterior, podríamos decir que\(\sqrt{5}\) está entre 2 y 3. Usando símbolos de desigualdad, escribimos

    \[2 < \sqrt{5} < 3\]

    Ejemplo\(\PageIndex{5}\):

    Estimar\(\sqrt{60}\) entre dos números enteros consecutivos.

    Solución

    Piensa en los cuadrados perfectos más cercanos a 60. Haz una mesita de estos cuadrados perfectos y sus raíces cuadradas.

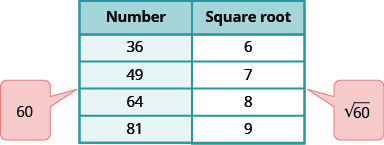
    Se muestra una tabla con 2 columnas. La primera columna está etiquetada como “Número” y contiene los valores: 36, 49, 64 y 81. Hay un globo saliendo de la mesa entre el 49 y el 64 que dice 60. La segunda columna está etiquetada como “Raíz cuadrada” y contiene los valores: 6, 7, 8 y 9. Hay un globo saliendo de la mesa entre 7 y 8 que dice raíz cuadrada de 60.

    Localiza 60 entre dos cuadrados perfectos consecutivos. 49 < 60 < 64
    \(\sqrt{60}\)está entre sus raíces cuadradas. $$7 <\ sqrt {60} < 8$$
    Ejercicio\(\PageIndex{9}\):

    Estimar\(\sqrt{38}\) entre dos números enteros consecutivos.

    Contestar

    \(6 < \sqrt{38} < 7 \)

    Ejercicio\(\PageIndex{10}\):

    Estimar\(\sqrt{84}\) entre dos números enteros consecutivos.

    Contestar

    \(9 < \sqrt{84} < 10 \)

    Colaboradores y Atribuciones

    This page titled 5.12: Simplificar y Usar Raíces Cuadradas (Parte 1) is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.