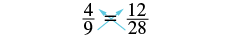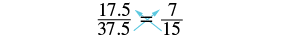Saltar al contenido principal
LibreTexts Español

6.5: Resolver proporciones y sus aplicaciones (Parte 1)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114305

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Usa la definición de proporción
    • Resolver proporciones
    • Resolver aplicaciones usando proporciones
    • Escribir ecuaciones porcentuales como proporciones
    • Traducir y resolver proporciones porcentuales
    ¡prepárate!

    Antes de comenzar, toma este cuestionario de preparación.

    1. Simplificar:\(\dfrac{\dfrac{1}{3}}{4}\). Si te perdiste este problema, revisa el Ejemplo 4.5.8.
    2. Resolver:\(\dfrac{x}{4}\) = 20. Si te perdiste este problema, revisa el Ejemplo 4.12.5.
    3. Escribe como tarifa: Sale montó su bicicleta 24 millas en 2 horas. Si te perdiste este problema, revisa el Ejemplo 5.10.6.

    Usar la Definición de Proporción

    En la sección de Ratios y Tarifas vimos algunas formas en que se utilizan en nuestra vida diaria. Cuando dos ratios o tasas son iguales, la ecuación que las relaciona se denomina proporción.

    Definición: proporcion

    Una proporción es una ecuación de la forma\(\dfrac{a}{b} = \dfrac{c}{d}\), donde b ≠ 0, d ≠ 0.

    La proporción indica que dos ratios o tasas son iguales. La proporción se lee “a es a b, como c es a d”.

    La ecuación\(\dfrac{1}{2} = \dfrac{4}{8}\) es una proporción porque las dos fracciones son iguales. La proporción\(\dfrac{1}{2} = \dfrac{4}{8}\) se lee “1 es a 2 como 4 es a 8”.

    Si comparamos cantidades con unidades, tenemos que estar seguros de que las estamos comparando en el orden correcto. Por ejemplo, en la proporción\(\dfrac{20\; students}{1\; teacher} = \dfrac{60\; students}{3\; teachers}\) comparamos el número de alumnos con el número de profesores. Ponemos a los alumnos en los numeradores y a los profesores en los denominadores.

    Ejemplo\(\PageIndex{1}\):

    Escribe cada oración en proporción: (a) 3 es a 7 como 15 es a 35. (b) 5 hits en 8 en murciélagos es lo mismo que 30 hits en 48 turnos al bate. (c) $1.50 por 6 onzas equivale a $2.25 por 9 onzas.

    Solución

    (a) 3 es a 7 como 15 es a 35

    Escribir como proporción. $$\ dfrac {3} {7} =\ dfrac {15} {35} $$

    (b) 5 hits en 8 en murciélagos es lo mismo que 30 hits en 48 turnos al bate

    Escribe cada fracción para comparar golpes con turnos al bate. $$\ dfrac {hits} {at-bats} =\ dfrac {hits} {at-bats} $$
    Escribir como proporción. $$\ dfrac {5} {8} =\ dfrac {30} {48} $$

    (c) $1.50 por 6 onzas equivale a $2.25 por 9 onzas

    Escribe cada fracción para comparar dólares con onzas. $$\ dfrac {\ $} {onzas} =\ dfrac {\ $} {onzas} $$
    Escribir como proporción. $$\ dfrac {1.50} {6} =\ dfrac {2.25} {9} $$
    Ejercicio\(\PageIndex{1}\):

    Escribe cada oración en proporción: (a) 5 es a 9 como 20 es a 36. (b) 7 hits en 11 turnos al bate es lo mismo que 28 hits en 44 turnos al bate. (c) $2.50 por 8 onzas equivale a $3.75 por 12 onzas.

    Responder a

    \(\frac{5}{9} = \frac{20}{36}\)

    Respuesta b

    \(\frac{7}{11} = \frac{28}{44}\)

    Respuesta c

    \(\frac{2.50}{8} = \frac{3.75}{12}\)

    Ejercicio\(\PageIndex{2}\):

    Escribe cada oración en proporción: (a) 6 es a 7 como 36 es a 42. b) 8 adultos para 36 niños es lo mismo que 12 adultos para 54 niños. (c) $3.75 por 6 onzas equivale a $2.50 por 4 onzas.

    Responder a

    \(\frac{6}{7} = \frac{36}{42}\)

    Respuesta b

    \(\frac{8}{36} = \frac{12}{54}\)

    Respuesta c

    \(\frac{3.75}{6} = \frac{2.50}{4}\)

    Mira las proporciones\(\dfrac{1}{2} = \dfrac{4}{8}\) y\(\dfrac{2}{3} = \dfrac{6}{9}\). De nuestro trabajo con fracciones equivalentes sabemos que estas ecuaciones son ciertas. Pero, ¿cómo sabemos si una ecuación es una proporción con fracciones equivalentes si contiene fracciones con números mayores? Para determinar si una proporción es verdadera, encontramos los productos cruzados de cada proporción. Para encontrar los productos cruzados, multiplicamos cada denominador con el numerador opuesto (diagonalmente a través del signo igual). Los resultados se denominan productos cruzados debido a la cruz formada. Los productos cruzados de una proporción son iguales.

    La figura muestra la multiplicación cruzada de dos proporciones. Ahí está la proporción 1 es a 2 ya que 4 es a 8. Las flechas se muestran diagonalmente a través del signo igual para mostrar productos cruzados. Las ecuaciones formadas por multiplicación cruzada son 8 · 1 = 8 y 2 · 4 = 8. Ahí está la proporción 2 es a 3 ya que 6 es a 9. Las flechas se muestran diagonalmente a través del signo igual para mostrar productos cruzados. Las ecuaciones formadas por multiplicación cruzada son 9 · 2 = 18 y 3 · 6 = 18.

    Definición: Productos cruzados de una proporción

    Para cualquier proporción de la forma\(\dfrac{a}{b} = \dfrac{c}{d}\), donde b ≠ 0, d ≠ 0, sus productos cruzados son iguales.

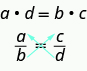
    Los productos cruzados se pueden usar para probar si una proporción es verdadera. Para probar si una ecuación hace una proporción, encontramos los productos cruzados. Si son iguales, tenemos una proporción.

    Ejemplo\(\PageIndex{2}\):

    Determinar si cada ecuación es una proporción: (a)\(\dfrac{4}{9} = \dfrac{12}{28}\) (b)\(\dfrac{17.5}{37.5} = \dfrac{7}{15}\)

    Solución

    Para determinar si la ecuación es una proporción, encontramos los productos cruzados. Si son iguales, la ecuación es una proporción.

    (a)\(\dfrac{4}{9} = \dfrac{12}{28}\)

    Encuentra los productos cruzados.

    \[28 \cdot 4 = 112 \qquad 9 \cdot 12 = 108\]

    Dado que los productos cruzados no son iguales, 28 · 4 ≠ 9 · 12, la ecuación no es una proporción.

    b)\(\dfrac{17.5}{37.5} = \dfrac{7}{15}\)

    Encuentra los productos cruzados.

    \[15 \cdot 17.5 = 262.5 \qquad 37.5 \cdot 7 = 262.5\]

    Dado que los productos cruzados son iguales, 15 • 17.5 = 37.5 • 7, la ecuación es una proporción.

    Ejercicio\(\PageIndex{3}\):

    Determinar si cada ecuación es una proporción: (a)\(\dfrac{7}{9} = \dfrac{54}{72}\) (b)\(\dfrac{24.5}{45.5} = \dfrac{7}{13}\)

    Responder a

    no

    Respuesta b

    si

    Ejercicio\(\PageIndex{4}\):

    Determinar si cada ecuación es una proporción: (a)\(\dfrac{8}{9} = \dfrac{56}{73}\) (b)\(\dfrac{28.5}{52.5} = \dfrac{8}{15}\)

    Responder a

    no

    Respuesta b

    no

    Resolver proporciones

    Para resolver una proporción que contiene una variable, recordamos que la proporción es una ecuación. Todas las técnicas que hemos utilizado hasta ahora para resolver ecuaciones siguen aplicándose. En el siguiente ejemplo, resolveremos una proporción multiplicando por el Mínimo Denominador Común (LCD) usando la Propiedad de Multiplicación de Igualdad.

    Ejemplo\(\PageIndex{3}\):

    Resolver:\(\dfrac{x}{63} =\dfrac{4}{7}\).

    Solución

    Para aislar x, multiplique ambos lados por la pantalla LCD, 63. $$\ textcolor {rojo} {63}\ izquierda (\ dfrac {x} {63}\ derecha) =\ textcolor {rojo} {63}\ izquierda (\ dfrac {4} {7}\ derecha) $$
    Simplificar. $$x =\ dfrac {9\ cdot\ cancel {7}\ cdot 4} {\ cancel {7}} $$
    Dividir los factores comunes. $$x = 36$$

    Consulta: Para verificar nuestra respuesta, sustituimos en la proporción original.

    Sustituto x =\(\textcolor{red}{36}\) $$\ dfrac {\ textcolor {rojo} {36}} {63}\ stackrel {?} {=}\ dfrac {4} {7} $$
    Mostrar factores comunes. $$\ dfrac {4\ cdot 9} {7\ cdot 9}\ stackrel {?} {=}\ dfrac {4} {7} $$
    Simplificar. $$\ dfrac {4} {7} =\ dfrac {4} {7}\;\ marca de verificación$$
    Ejercicio\(\PageIndex{5}\):

    Resolver la proporción:\(\dfrac{n}{84} = \dfrac{11}{12}\).

    Responder

    77

    Ejercicio\(\PageIndex{6}\):

    Resolver la proporción:\(\dfrac{y}{96} = \dfrac{13}{12}\).

    Responder

    104

    Cuando la variable está en un denominador, usaremos el hecho de que los productos cruzados de una proporción son iguales para resolver las proporciones.

    Podemos encontrar los productos cruzados de la proporción y luego ponerlos iguales. Luego resolvemos la ecuación resultante utilizando nuestras técnicas familiares.

    Ejemplo\(\PageIndex{4}\):

    Resolver:\(\dfrac{144}{a} =\dfrac{9}{4}\).

    Solución

    Observe que la variable está en el denominador, por lo que resolveremos encontrando los productos cruzados y poniéndolos iguales.

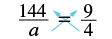
    Encuentra los productos cruzados y ponlos iguales. 4 • 144 = a • 9
    Simplificar. 576 = 9a
    Divide ambos lados por 9. $$\ dfrac {576} {9} =\ dfrac {9a} {9} $$
    Simplificar. $64 = a$$

    Comprueba tu respuesta.

    Sustituir a =\(\textcolor{red}{64}\) $$\ dfrac {144} {\ textcolor {rojo} {64}}\ stackrel {?} {=}\ dfrac {9} {4} $$
    Mostrar factores comunes. $$\ dfrac {9\ cdot 16} {4\ cdot 16}\ stackrel {?} {=}\ dfrac {9} {4} $$
    Simplificar. $$\ dfrac {9} {4} =\ dfrac {9} {4}\;\ marca de verificación$$

    Otro método para resolver esto sería multiplicar ambos lados por la LCD, 4a. Pruébalo y verifica que obtienes la misma solución.

    Ejercicio\(\PageIndex{7}\):

    Resolver la proporción:\(\dfrac{91}{b} = \dfrac{7}{5}\).

    Responder

    65

    Ejercicio\(\PageIndex{8}\):

    Resolver la proporción:\(\dfrac{39}{c} = \dfrac{13}{8}\).

    Responder

    24

    Ejemplo\(\PageIndex{5}\):

    Resolver:\(\dfrac{52}{91} = \dfrac{-4}{y}\)

    Solución

    Encuentra los productos cruzados y ponlos iguales.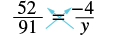
      y • 52 = 91 (-4)
    Simplificar. 52 años = -364
    Divide ambos lados por 52. $$\ dfrac {52} {52} =\ dfrac {-364} {52} $$
    Simplificar. $$y = -7$$

    Comprobar:

    Sustituto y =\(\textcolor{red}{-7}\) $$\ dfrac {52} {91}\ stackrel {?} {=}\ dfrac {-4} {\ textcolor {rojo} {-7}} $$
    Mostrar factores comunes. $$\ dfrac {13\ cdot 4} {13\ cdot 7}\ stackrel {?} {=}\ dfrac {-4} {\ textcolor {rojo} {-7}} $$
    Simplificar. $$\ dfrac {4} {7} =\ dfrac {4} {7}\;\ marca de verificación$$
    Ejercicio\(\PageIndex{9}\):

    Resolver la proporción:\(\dfrac{84}{98} = \dfrac{-6}{x}\).

    Responder

    -7

    Ejercicio\(\PageIndex{10}\):

    Resolver la proporción:\(\dfrac{-7}{y} = \dfrac{105}{135}\).

    Responder

    -9

    Resolver aplicaciones usando proporciones

    La estrategia para resolver aplicaciones que hemos utilizado anteriormente en este capítulo, también funciona para proporciones, ya que las proporciones son ecuaciones. Cuando establecemos la proporción, debemos asegurarnos de que las unidades sean correctas—las unidades en los numeradores coinciden y las unidades en los denominadores coinciden.

    Ejemplo\(\PageIndex{6}\):

    Cuando los pediatras recetan paracetamol a los niños, prescriben 5 mililitros (ml) de acetaminofén por cada 25 libras del peso del niño. Si Zoe pesa 80 libras, ¿cuántos mililitros de acetaminofén le recetará su médico?

    Solución

    Identifica lo que te piden encontrar. ¿Cuántos ml de acetaminofén recetará el médico?
    Elija una variable para representarla. Dejar a = ml de acetaminofén.
    Escribe una frase que dé la información para encontrarla. Si se recetan 5 ml por cada 25 libras, ¿cuánto se recetará por 80 libras?
    Traducir en una proporción. $$\ dfrac {ml} {libras} =\ dfrac {ml} {libras}\ tag {6.5.24} $$
    Sustituir valores dados: tenga cuidado con las unidades. $$\ dfrac {5} {25} =\ dfrac {a} {80}\ tag {6.5.25} $$
    Multiplica ambos lados por 80. $$80\ cdot\ dfrac {5} {25} = 80\ cdot\ dfrac {a} {80}\ tag {6.5.26} $$
    Multiplicar y mostrar factores comunes. $$\ dfrac {16\ cdot 5\ cdot 5} {5\ cdot 5} =\ dfrac {80a} {80}\ tag {6.5.27} $$
    Simplificar. $$16 = a\ tag {6.5.28} $$
    Comprueba si la respuesta es razonable. Sí. Ya que 80 es aproximadamente 3 veces 25, el medicamento debe ser aproximadamente 3 veces 5.
    Escribe una oración completa. El pediatra le recetaría 16 ml de acetaminofén a Zoe.

    También podrías resolver esta proporción estableciendo iguales los productos cruzados.

    Ejercicio\(\PageIndex{11}\):

    Los pediatras prescriben 5 mililitros (ml) de acetaminofén por cada 25 libras del peso de un niño. ¿Cuántos mililitros de acetaminofén le recetará el médico a Emilia, quien pesa 60 libras?

    Responder

    12 ml

    Ejercicio\(\PageIndex{12}\):

    Por cada 1 kilogramo (kg) de peso de un niño, los pediatras prescriben 15 miligramos (mg) de un reductor de fiebre. Si Isabella pesa 12 kg, ¿cuántos miligramos del reductor de fiebre prescribirá el pediatra?

    Responder

    180 mg

    Ejemplo\(\PageIndex{7}\):

    Una marca de palomitas de maíz para microondas tiene 120 calorías por porción. Una bolsa entera de estas palomitas tiene 3.5 porciones. ¿Cuántas calorías hay en una bolsa entera de estas palomitas de maíz para microondas?

    Solución

    Identifica lo que te piden encontrar. ¿Cuántas calorías hay en una bolsa entera de palomitas de maíz para microondas?
    Elija una variable para representarla. Dejar c = número de calorías.
    Escribe una frase que dé la información para encontrarla. Si hay 120 calorías por porción, ¿cuántas calorías hay en una bolsa entera con 3.5 porciones?
    Traducir en una proporción. $$\ dfrac {calorías} {porción} =\ dfrac {calorías} {porción}\ tag {6.5.29} $$
    Sustituir valores dados. $$\ dfrac {120} {1} =\ dfrac {c} {3.5}\ tag {6.5.30} $$
    Multiplica ambos lados por 3.5. $$ (3.5)\ izquierda (\ dfrac {120} {1}\ derecha) = (3.5)\ izquierda (\ dfrac {c} {3.5}\ derecha)\ tag {6.5.31} $$
    Multiplicar. $420 = c\ tag {6.5.32} $$
    Comprueba si la respuesta es razonable. Sí. Dado que 3.5 está entre 3 y 4, las calorías totales deben estar entre 360 (3 • 120) y 480 (4 • 120).
    Escribe una oración completa. Toda la bolsa de palomitas de maíz microondas tiene 420 calorías.
    Ejercicio\(\PageIndex{13}\):

    A Marissa le encanta el Caramel Macchiato en la cafetería. El tamaño mediano de 16 oz. tiene 240 calorías. ¿Cuántas calorías obtendrá si bebe la talla grande de 20 oz?

    Responder

    300

    Ejercicio\(\PageIndex{14}\):

    A Yaneli le encantan los dulces Starburst, pero quiere mantener sus refrigerios a 100 calorías. Si los caramelos tienen 160 calorías por 8 piezas, ¿cuántas piezas puede tener en su merienda?

    Responder

    5

    Ejemplo\(\PageIndex{8}\):

    Josías se fue a México para las vacaciones de primavera y cambió 325 dólares en pesos mexicanos. En ese momento, el tipo de cambio tenía $1 US es igual a 12.54 pesos mexicanos. ¿Cuántos pesos mexicanos obtuvo para su viaje?

    Solución

    Identifica lo que te piden encontrar. ¿Cuántos pesos mexicanos obtuvo Josías?
    Elija una variable para representarla. Dejar p = número de pesos.
    Escribe una frase que dé la información para encontrarla. Si $1 US es igual a 12.54 pesos mexicanos, entonces $325 es ¿cuántos pesos?
    Traducir en una proporción. $$\ dfrac {\ $} {pesos} =\ dfrac {\ $} {pesos}\ tag {6.5.33} $$
    Sustituir valores dados. $$\ dfrac {1} {12.54} =\ dfrac {325} {p}\ tag {6.5.34} $$
    La variable está en el denominador, así que encuentra los productos cruzados y ponlos iguales. $$p\ cdot 1 = 12.54 (325)\ tag {6.5.35} $$
    Simplificar. $$c = 4.075.5\ tag {6.5.36} $$
    Comprueba si la respuesta es razonable. Sí, $100 serían $1,254 pesos. $325 es un poco más de 3 veces esta cantidad.
    Escribe una oración completa. Josías tiene 4075.5 pesos para su viaje de vacaciones de primavera.
    Ejercicio\(\PageIndex{15}\):

    Yurianna va a Europa y quiere cambiar 800 dólares en euros. Al tipo de cambio actual, $1 US es igual a 0.738 Euro. ¿Cuántos euros tendrá para su viaje?

    Responder

    590 Euros

    Ejercicio\(\PageIndex{16}\):

    Corey y Nicole viajan a Japón y necesitan cambiar 600 dólares por yenes japoneses. Si cada dólar es 94.1 yenes, ¿cuántos yenes obtendrán?

    Responder

    56,460 yenes

    Colaboradores y Atribuciones

    This page titled 6.5: Resolver proporciones y sus aplicaciones (Parte 1) is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.