7.3: Propiedades conmutativas y asociativas (Parte 2)
- Page ID
- 114161
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Simplificar expresiones mediante las propiedades conmutativas y asociativas
Cuando tenemos que simplificar las expresiones algebraicas, a menudo podemos facilitar el trabajo aplicando primero la Propiedad Conmutativa o Asociativa en lugar de seguir automáticamente el orden de las operaciones. Observe que en el Ejemplo 7.2.4 la parte (b) era más fácil de simplificar que la parte (a) porque los opuestos estaban uno al lado del otro y su suma es 0. De igual manera, la parte (b) del Ejemplo 7.2.5 fue más fácil, con los recíprocos agrupados, porque su producto es 1. En los siguientes ejemplos, usaremos nuestro sentido numérico para buscar formas de aplicar estas propiedades para facilitar nuestro trabajo.
Simplificar: −84n + (−73n) + 84n.
Solución
Observe que los términos primero y tercero son opuestos, por lo que podemos usar la propiedad conmutativa de adición para reordenar los términos.
| Vuelva a ordenar los términos. | −84n + 84n + (−73n) |
| Añadir de izquierda a derecha. | 0 + (−73n) |
| Agregar. | −73n |
Simplificar: −27a + (−48a) + 27a.
- Contestar
-
\(-48a\)
Simplificar: 39x + (−92x) + (−39x).
- Contestar
-
\(-92x\)
Ahora veremos cómo es útil reconocer los recíprocos. Antes de multiplicar de izquierda a derecha, busque reciprocales—su producto es 1.
Simplificar:\(\dfrac{7}{15} \cdot \dfrac{8}{23} \cdot \dfrac{15}{7}\).
Solución
Observe que los términos primero y tercero son recíprocos, por lo que podemos usar la Propiedad Conmutativa de Multiplicación para reordenar los factores.
| Vuelva a ordenar los términos. | $$\ dfrac {7} {15}\ cdot\ dfrac {15} {7}\ cdot\ dfrac {8} {23} $$ |
| Multiplicar de izquierda a derecha. | $$1\ cdot\ dfrac {8} {23} $$ |
| Multiplicar. | $$\ dfrac {8} {23} $$ |
Simplificar:\(\dfrac{9}{16} \cdot \dfrac{5}{49} \cdot \dfrac{16}{9}\).
- Contestar
-
\(\frac{5}{49}\)
Simplificar:\(\dfrac{6}{17} \cdot \dfrac{11}{25} \cdot \dfrac{17}{6}\).
- Contestar
-
\(\frac{11}{25}\)
En las expresiones en las que necesitamos sumar o restar tres o más fracciones, primero combine aquellas con un denominador común.
Simplificar:\(\left(\dfrac{5}{13} + \dfrac{3}{4}\right) + \dfrac{1}{4}\).
Solución
Observe que los términos segundo y tercero tienen un denominador común, por lo que este trabajo será más fácil si cambiamos la agrupación.
| Agrupar los términos con un denominador común. | $$\ dfrac {5} {13} +\ izquierda (\ dfrac {3} {4} +\ dfrac {1} {4}\ derecha) $$ |
| Agregue primero entre paréntesis. | $$\ dfrac {5} {13} +\ izquierda (\ dfrac {4} {4}\ derecha) $$ |
| Simplifica la fracción. | $$\ dfrac {5} {13} + 1$$ |
| Agregar. | $$1\ dfrac {5} {13} $$ |
| Convertir a una fracción impropia. | $$\ dfrac {18} {13} $$ |
Simplificar:\(\left(\dfrac{7}{15} + \dfrac{5}{8}\right) + \dfrac{3}{8}\).
- Contestar
-
\(\frac{22}{15}\)
Simplificar:\(\left(\dfrac{2}{9} + \dfrac{7}{12}\right) + \dfrac{5}{12}\).
- Contestar
-
\(\frac{11}{9}\)
Al sumar y restar tres o más términos que involucren decimales, busque términos que se combinen para dar números enteros.
Simplificar: (6.47q + 9.99q) + 1.01q.
Solución
Observe que la suma del segundo y tercer coeficiente es un número entero.
| Cambiar la agrupación. | 6.47q + (9.99q + 1.01q) |
| Agregue primero entre paréntesis. | 6.47q + (11.00q) |
| Agregar. | 17.47q |
Muchas personas tienen buen sentido numérico cuando tratan con dinero. Piensa en sumar 99 centavos y 1 centavo. ¿Ves cómo se aplica esto para sumar 9.99 + 1.01?
Simplificar: (5.58c + 8.75c) + 1.25c.
- Contestar
-
\(15.58c\)
Simplificar: (8.79d + 3.55d) + 5.45d.
- Contestar
-
\(17.79d\)
No importa lo que estés haciendo, siempre es una buena idea pensar en el futuro. Al simplificar una expresión, piensa en cuáles serán tus pasos. El siguiente ejemplo te mostrará cómo usar la Propiedad Asociativa de Multiplicación puede hacer que tu trabajo sea más fácil si planeas con anticipación.
Simplifica la expresión: [1.67 (8)] (0.25).
Solución
Observe que multiplicar (8) (0.25) es más fácil que multiplicar 1.67 (8) porque da un número entero. (Piensa en tener 8 cuartos, eso hace $2.)
| Reagruparse. | 1.67 [(8) (0.25)] |
| Multiplique primero entre corchetes. | 1.67 [2] |
| Multiplicar. | 3.34 |
Simplificar: [1.17 (4)] (2.25).
- Contestar
-
\(10.53\)
Simplificar: [3.52 (8)] (2.5).
- Contestar
-
\(70.4\)
Al simplificar expresiones que contienen variables, podemos usar las propiedades conmutativas y asociativas para reordenar o reagrupar términos, como se muestra en el siguiente par de ejemplos.
Simplificar: 6 (9x).
Solución
| Utilice la propiedad asociativa de la multiplicación para reagrupar. | (6 • 9) x |
| Multiplicar entre paréntesis. | 54x |
Simplificar: 8 (3y).
- Contestar
-
\(24y\)
Simplificar: 12 (5z).
- Contestar
-
\(60z\)
En El lenguaje del álgebra aprendimos a combinar términos similares reordenando una expresión para que los términos similares estuvieran juntos. Simplificamos la expresión 3x + 7 + 4x + 5 reescribiéndola como 3x + 4x + 7 + 5 y luego la simplificamos a 7x + 12. Estábamos usando la Propiedad Conmutativa de Adición.
Simplificar: 18p + 6q + (−15p) + 5q.
Solución
Utilice la Propiedad Conmutativa de Adición para reordenar de manera que los términos similares estén juntos.
| Términos de reordenar. | 18p + (−15p) + 6q + 5q |
| Combina términos similares. | 3p + 11q |
Simplificar: 23r + 14s + 9r + (−15s).
- Contestar
-
\(32r-s\)
Simplificar: 37m + 21n + 4m + (−15n).
- Contestar
-
\(41m+6n\)
La práctica hace la perfección
Utilizar las propiedades conmutativas y asociativas
En los siguientes ejercicios, utilice las propiedades conmutativas para reescribir la expresión dada.
- 8 + 9 = ___
- 7 + 6 = ___
- 8 (−12) = ___
- 7 (−13) = ___
- (−19) (−14) = ___
- (−12) (−18) = ___
- −11 + 8 = ___
- −15 + 7 = ___
- x + 4 = ___
- y + 1 = ___
- −2a = ___
- −3m = ___
En los siguientes ejercicios, utilice las propiedades asociativas para reescribir la expresión dada.
- (11 + 9) + 14 = ___
- (21 + 14) + 9 = ___
- (12 · 5) • 7 = ___
- (14 · 6) • 9 = ___
- (−7 + 9) + 8 = ___
- (−2 + 6) + 7 = ___
- \ (\ izquierda (16\ cdot\ dfrac {4} {5}\ derecha) • 15 = ___
- \ (\ izquierda (13\ cdot\ dfrac {2} {3}\ derecha) • 18 = ___
- 3 (4x) = ___
- 4 (7x) = ___
- (12 + x) + 28 = ___
- (17 + y) + 33 = ___
Evaluar expresiones usando las propiedades conmutativas y asociativas
En los siguientes ejercicios, evalúe cada expresión para el valor dado.
- Si y =\(\dfrac{5}{8}\), evalúe:
- y + 0.49 + (− y)
- y + (− y) + 0.49
- Si z =\(\dfrac{7}{8}\), evalúe:
- z + 0.97 + (− z)
- z + (− z) + 0.97
- Si c =\(− \dfrac{11}{4}\), evaluar:
- c + 3.125 + (− c)
- c + (− c) + 3.125
- Si d =\(− \dfrac{9}{4}\), evaluar:
- d + 2.375 + (− d)
- d + (− d) + 2.375
- Si j = 11, evalúe:
- \(\dfrac{5}{6} \left(\dfrac{6}{5} j \right)\)
- \(\left(\dfrac{5}{6} \cdot \dfrac{6}{5}\right)j\)
- Si k = 21, evalúe:
- \(\dfrac{4}{13} \left(\dfrac{13}{4}k \right)\)
- \(\left(\dfrac{4}{13} \cdot \dfrac{13}{4}\right)k\)
- Si m = −25, evalúe:
- \(- \dfrac{3}{7} \left(\dfrac{7}{3}m \right)\)
- \(\left(- \dfrac{3}{7} \cdot \dfrac{7}{3}\right)m\)
- Si n = −8, evalúe:
- \(- \dfrac{5}{21} \left(\dfrac{21}{5}n \right)\)
- \(\left(- \dfrac{5}{21} \cdot \dfrac{21}{5}\right)n\)
Simplificar expresiones mediante las propiedades conmutativas y asociativas
En los siguientes ejercicios, simplifique.
- −45a + 15 + 45a
- 9y + 23 + (−9y)
- \(\dfrac{1}{2} + \dfrac{7}{8} + \left(− \dfrac{1}{2}\right)\)
- \(\dfrac{2}{5} + \dfrac{5}{12} + \left(− \dfrac{2}{5}\right)\)
- \(\dfrac{3}{20} \cdot \dfrac{49}{11} \cdot \dfrac{20}{3}\)
- \(\dfrac{13}{18} \cdot \dfrac{25}{7} \cdot \dfrac{18}{13}\)
- \(\dfrac{7}{12} \cdot \dfrac{9}{17} \cdot \dfrac{24}{7}\)
- \(\dfrac{3}{10} \cdot \dfrac{13}{23} \cdot \dfrac{50}{3}\)
- −24 • 7 •\(\dfrac{3}{8}\)
- −36 • 11 •\(\dfrac{4}{9}\)
- \(\left(\dfrac{5}{6} + \dfrac{8}{15}\right) + \dfrac{7}{15}\)
- \(\left(\dfrac{1}{12} + \dfrac{4}{9}\right) + \dfrac{5}{9}\)
- \(\dfrac{5}{13} + \dfrac{3}{4} + \dfrac{1}{4}\)
- \(\dfrac{8}{15} + \dfrac{5}{7} + \dfrac{2}{7}\)
- (4.33p + 1.09p) + 3.91p
- (5.89d + 2.75d) + 1.25d
- 17 (0.25) (4)
- 36 (0.2) (5)
- [2.48 (12)] (0.5)
- [9.731 (4)] (0.75)
- 7 (4a)
- 9 (8w)
- −15 (5m)
- −23 (2n)
- 12\(\left(\dfrac{5}{6} p\right)\)
- 20\(\left(\dfrac{3}{5} q\right)\)
- 14x + 19y + 25x + 3años
- 15u + 11v + 27u + 19v
- 43m + (−12n) + (−16m) + (−9n)
- −22p + 17q + (−35p) + (−27q)
- \(\dfrac{3}{8}g + \dfrac{1}{12}h + \dfrac{7}{8}g + \dfrac{5}{12}h\)
- \(\dfrac{5}{6}a + \dfrac{3}{10}b + \dfrac{1}{6}a + \dfrac{9}{10}b\)
- 6.8p + 9.14q + (−4.37p) + (−0.88q)
- 9.6m + 7.22n + (−2.19m) + (−0.65n)
Matemáticas cotidianas
- Sellos Allie y Loren necesitan comprar sellos. Allie necesita cuatro sellos de $0.49 y nueve sellos de $0.02. Loren necesita ocho sellos de $0.49 y tres sellos de $0.02.
- ¿Cuánto costarán los sellos de Allie?
- ¿Cuánto costarán los sellos de Loren?
- ¿Cuál es el costo total de los sellos de las niñas?
- ¿Cuántos sellos de $0.49 necesitan las chicas en conjunto? ¿Cuánto van a costar?
- ¿Cuántos sellos de $0.02 necesitan las chicas en conjunto? ¿Cuánto van a costar?
- Contar Cash Grant es sumar el efectivo de una cena de recaudación de fondos. En un sobre, tiene veintitrés billetes de 5 dólares, dieciocho billetes de 10 dólares y treinta y cuatro billetes de 20 dólares. En otro sobre, tiene catorce billetes de 5 dólares, nueve billetes de 10 dólares y veintisiete billetes de 20 dólares.
- ¿Cuánto dinero hay en el primer sobre?
- ¿Cuánto dinero hay en el segundo sobre?
- ¿Cuál es el valor total de todo el efectivo?
- ¿Cuál es el valor de todos los billetes de $5?
- ¿Cuál es el valor de todos los billetes de $10?
- ¿Cuál es el valor de todos los billetes de $20?
Ejercicios de escritura
- En sus propias palabras, diga la Propiedad Conmutativa de Adición y explique por qué es útil.
- En sus propias palabras, diga la Propiedad Asociativa de la Multiplicación y explique por qué es útil.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
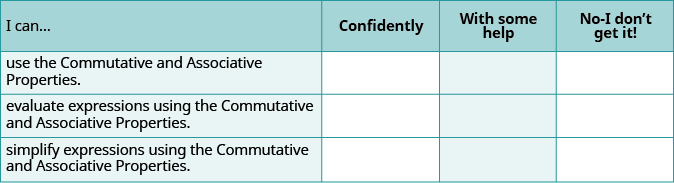
(b) Después de revisar esta lista de verificación, ¿qué hará para confiar en todos los objetivos?