Inicio
Matemáticas
Pre-Álgebra
Libro: Preálgebra (OpenStax)
11: Gráficas
11.7: Comprender la pendiente de una línea (Parte 1)

11.7: Comprender la pendiente de una línea (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114232

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Usar geotableros para modelar taludes
Encuentra la pendiente de una línea a partir de su gráfica
Encuentra la pendiente de las líneas horizontales y verticales
Utilice la fórmula de pendiente para encontrar el talud de una línea entre dos puntos
Graficar una línea dada un punto y la pendiente
Resolver aplicaciones de pendientes

¡prepárate!

Antes de comenzar, toma este cuestionario de preparación.

Simplificar:$\dfrac{1 − 4}{8 − 2}$. Si te perdiste este problema, revisa el Ejemplo 4.6.12.
Dividir:$\dfrac{0}{4}, \dfrac{4}{0}$. Si te perdiste este problema, revisa el Ejemplo 7.5.5.
Simplificar:$\dfrac{15}{-3}, \dfrac{−15}{3}, \dfrac{−15}{−3}$. Si te perdiste este problema, revisa el Ejemplo 4.6.11.

Como hemos estado graficando ecuaciones lineales, hemos visto que algunas líneas se inclinan hacia arriba a medida que van de izquierda a derecha y algunas líneas se inclinan hacia abajo. Algunas líneas son muy empinadas y algunas líneas son más planas. ¿Qué determina si una línea se inclina hacia arriba o hacia abajo, y si su inclinación es empinada o plana?

La pendiente de la inclinación de una línea se llama pendiente de la línea. El concepto de talud tiene muchas aplicaciones en el mundo real. El cabeceo de un techo y el rasante de una autopista o rampa para sillas de ruedas son solo algunos ejemplos en los que literalmente se ven pendientes. Y cuando montas en bicicleta, sientes la pendiente mientras bombeas cuesta arriba o cuesta abajo en la costa.

Uso de geoplacas para modelar taludes

En esta sección, exploraremos los conceptos de pendiente.

El uso de bandas de goma en una geoplaca proporciona una forma concreta de modelar líneas en una cuadrícula de coordenadas. Al estirar una banda de goma entre dos clavijas en una geobordo, podemos descubrir cómo encontrar la pendiente de una línea. Y cuando montas en bicicleta, sientes la pendiente mientras bombeas cuesta arriba o cuesta abajo en la costa.

Comenzaremos estirando una banda de goma entre dos clavijas para hacer una línea como se muestra en la Figura$\PageIndex{1}$.

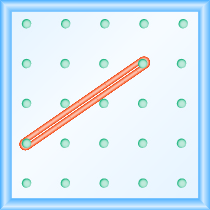
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 4 y el punto en la columna 4 fila 2.$

Figura$\PageIndex{1}$

¿Se ve como una línea?

Ahora estiramos una parte de la banda de goma recta hacia arriba desde la clavija izquierda y alrededor de una tercera clavija para hacer los lados de un triángulo rectángulo como se muestra en la Figura$\PageIndex{2}$. Cuidadosamente hacemos un ángulo de 90° alrededor de la tercera clavija, de manera que un lado es vertical y el otro es horizontal.

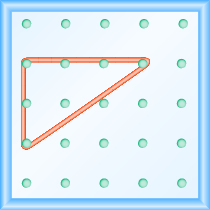
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un triángulo estilo banda elástica que conecta tres de los tres puntos en la columna 1 fila 2, columna 1 fila 4 y columna 4 fila 2.$

Figura$\PageIndex{2}$

Para encontrar la pendiente de la línea, medimos la distancia a lo largo de las patas verticales y horizontales del triángulo. A la distancia vertical se le llama subida y a la distancia horizontal se le llama recorrido, como se muestra en la Figura$\PageIndex{3}$.

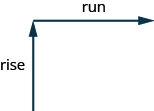
$Esta figura muestra dos flechas. La primera flecha es vertical y está etiquetada como “subir”. La segunda flecha comienza al final de la primera flecha que se extiende hacia la derecha y se etiqueta como “correr”.$

Figura$\PageIndex{3}$

Para ayudar a recordar los términos, puede ayudar pensar en las imágenes que se muestran en la Figura$\PageIndex{4}$.

$...$

Figura$\PageIndex{4}$

En nuestro geoboard, la subida es de 2 unidades debido a que la banda de goma sube 2 espacios en la pata vertical. Ver Figura$\PageIndex{5}$.

¿Cuál es la carrera? ¡Asegúrate de contar los espacios entre las clavijas en lugar de las propias clavijas! La banda de goma atraviesa 3 espacios en la pata horizontal, por lo que la carrera es de 3 unidades.

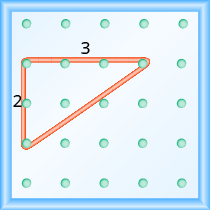
Figura$\PageIndex{5}$

La pendiente de una línea es la relación entre la subida y la carrera. Entonces la pendiente de nuestra línea es$\dfrac{2}{3}$. En matemáticas, la pendiente siempre está representada por la letra m.

Definición: Pendiente de una línea

La pendiente de una línea es m =$\dfrac{rise}{run}$.

La subida mide el cambio vertical y la corrida mide el cambio horizontal.

¿Cuál es la pendiente de la línea en el geobordo en la Figura$\PageIndex{5}$?

\[\begin{split} m &= \dfrac{rise}{run} \\ m &= \dfrac{2}{3} \\ The\; line\; &has\; slope\; \dfrac{2}{3} \ldotp \end{split}\]

Cuando trabajamos con geoboards, es una buena idea tener el hábito de comenzar por una clavija a la izquierda y conectarnos a una clavija a la derecha. Después estiramos la banda de goma para formar un triángulo rectángulo.

Si empezamos por subir la subida es positiva, y si la estiramos hacia abajo la subida es negativa. Vamos a contar la carrera de izquierda a derecha, así como leíste este párrafo, por lo que la carrera será positiva.

Dado que la fórmula de pendiente tiene subida sobre carrera, puede ser más fácil contar siempre primero la subida y luego la carrera.

Ejemplo$\PageIndex{1}$:

¿Cuál es la pendiente de la línea en el geobordo que se muestra?

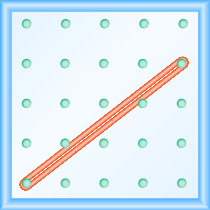
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 5 y el punto en la columna 5 fila 2.$

Solución

Utilice la definición de talud.

\[m = \dfrac{rise}{run}\]

Comienza por la clavija izquierda y haz un triángulo rectángulo estirando la goma elástica hacia arriba y hacia la derecha para llegar a la segunda clavija. Contar la subida y la carrera como se muestra.

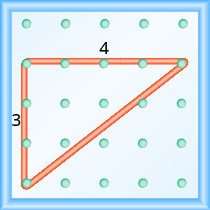
El ascenso es de 3 unidades. \[m = \dfrac{3}{run}\]

La carrera es de 4 unidades. \[m = \dfrac{3}{4}\]

La pendiente es$\dfrac{3}{4}$.

Ejercicio$\PageIndex{1}$:

¿Cuál es la pendiente de la línea en el geobordo que se muestra?

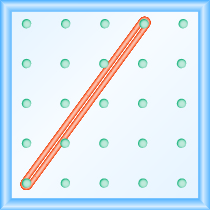
Responder: $\frac{4}{3}$

Ejercicio$\PageIndex{2}$:

¿Cuál es la pendiente de la línea en el geobordo que se muestra?

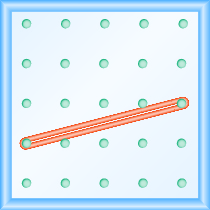
Responder: $\frac{1}{4}$

Ejemplo$\PageIndex{2}$:

¿Cuál es la pendiente de la línea en el geobordo que se muestra?

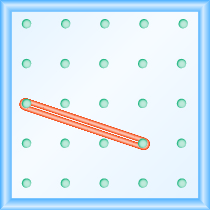
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 3 y el punto en la columna 4 fila 4.$

Solución

Utilice la definición de talud.

\[m = \dfrac{rise}{run}\]

Comienza por la clavija izquierda y haz un triángulo rectángulo estirando la banda de goma hasta la clavija de la derecha. Esta vez necesitamos estirar la banda de goma hacia abajo para hacer la pierna vertical, por lo que la subida es negativa.

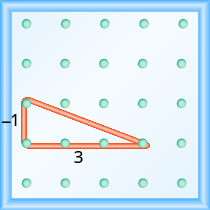
La subida es −1.

\[m = \dfrac{−1}{run}\]

La carrera es 3.

\[\begin{split} m &= \dfrac{−1}{3} \\ m &= − \dfrac{1}{3} \end{split}\]

La pendiente es$− \dfrac{1}{3}$.

Ejercicio$\PageIndex{3}$:

¿Cuál es la pendiente de la línea en el geobordo?

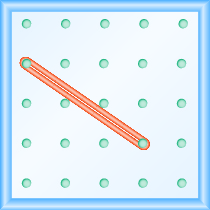
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 2 y el punto en la columna 4 fila 4.$

Responder: $-\frac{2}{3}$

Ejercicio$\PageIndex{4}$:

¿Cuál es la pendiente de la línea en el geobordo?

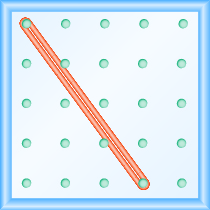
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 1 y el punto en la columna 4 fila 5.$

Responder: $-\frac{4}{3}$

Observe que en el primer ejemplo, la pendiente es positiva y en el segundo ejemplo la pendiente es negativa. ¿Se nota alguna diferencia en las dos líneas que se muestran en la$\PageIndex{6}$ Figura?

$...$

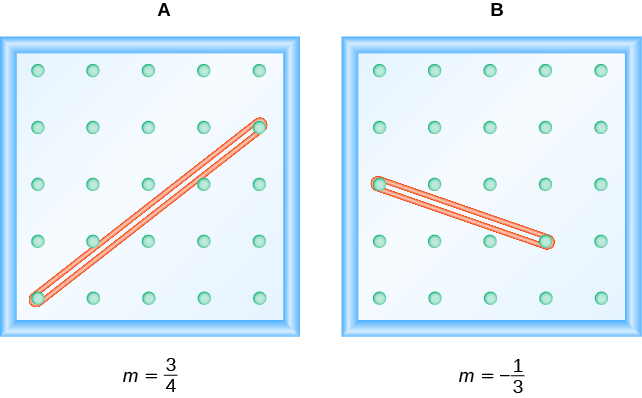
Figura$\PageIndex{6}$

Al leer de izquierda a derecha, la línea de la Figura A, va subiendo; tiene pendiente positiva. La línea Figura B va bajando; tiene pendiente negativa.

$...$

Figura$\PageIndex{7}$

Ejemplo$\PageIndex{3}$:

Utilice un geoboard para modelar una línea con pendiente$\frac{1}{2}$.

Solución

Para modelar una línea con una pendiente específica en un geobordo, necesitamos conocer la subida y la carrera.

Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Reemplazar m con$\dfrac{1}{2}$.	$$\ dfrac {1} {2} =\ dfrac {subida} {correr} $$

Entonces, la subida es de 1 unidad y la carrera es de 2 unidades.

Comienza en una clavija en la parte inferior izquierda del geoboard. Estire la banda elástica hasta 1 unidad, y luego a la derecha 2 unidades.

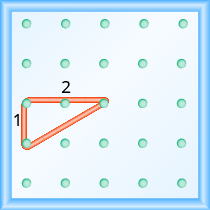
La hipotenusa del triángulo rectángulo formado por la banda elástica representa una línea con una pendiente de$\dfrac{1}{2}$.

Ejercicio$\PageIndex{5}$:

Utilice un geoboard para modelar una línea con la pendiente dada: m =$\dfrac{1}{3}$.

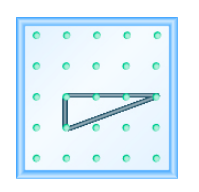
Responder: $La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un triángulo estilo banda elástica que conecta tres de los tres puntos en la columna 2 fila 3, columna 2 fila 4 y columna 5 fila 3.$

Ejercicio$\PageIndex{6}$:

Utilice un geoboard para modelar una línea con la pendiente dada: m =$\dfrac{3}{2}$.

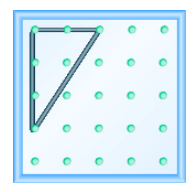
Responder: $La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un triángulo estilo banda elástica que conecta tres de los tres puntos en la columna 1 fila 1, columna 1 fila 4 y columna 3 fila 1.$

Ejemplo$\PageIndex{4}$:

Utilice un geoboard para modelar una línea con pendiente$\dfrac{−1}{4}$.

Solución

Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Reemplazar m con$− \dfrac{1}{4}$.	$$-\ dfrac {1} {4} =\ dfrac {subida} {correr} $$

Entonces, la subida es −1 y la carrera es 4.

Dado que la subida es negativa, elegimos una clavija inicial en la parte superior izquierda que nos dará espacio para la cuenta regresiva. Estiramos la banda de goma hacia abajo 1 unidad, luego a la derecha 4 unidades.

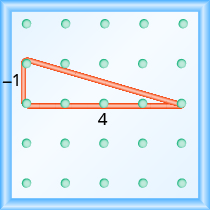
La hipotenusa del triángulo rectángulo formado por la banda elástica representa una línea cuya pendiente es$− \dfrac{1}{4}$.

Ejercicio$\PageIndex{7}$:

Utilice un geoboard para modelar una línea con la pendiente dada: m =$\dfrac{−3}{2}$.

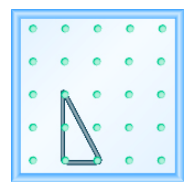
Responder: $La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un triángulo estilo banda elástica que conecta tres de los tres puntos en la columna 2 fila 3, columna 2 fila 5 y columna 3 fila 5.$

Ejercicio$\PageIndex{8}$:

Utilice un geoboard para modelar una línea con la pendiente dada: m =$\dfrac{−1}{3}$.

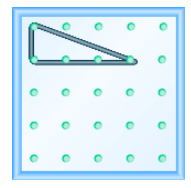
Responder: $La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un triángulo estilo banda elástica que conecta tres de los tres puntos en la columna 1 fila 1, columna 1 fila 2 y columna 4 fila 2.$

Encuentra la Pendiente de una Línea a partir de su Gráfica

Ahora veremos algunas gráficas en una cuadrícula de coordenadas para encontrar sus pendientes. El método será muy similar al que acabamos de modelar en nuestras geoplacas.

Para encontrar la pendiente, debemos contar la subida y la carrera. Pero, ¿por dónde empezamos?

Localizamos dos puntos cualesquiera en la línea. Intentamos elegir puntos con coordenadas que sean enteros para facilitar nuestros cálculos. Luego comenzamos con el punto de la izquierda y dibujamos un triángulo rectángulo, para que podamos contar la subida y la carrera.

Ejemplo$\PageIndex{5}$:

Encuentra la pendiente de la línea que se muestra:

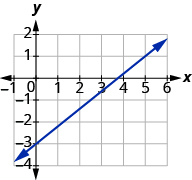
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 6. El eje y va de -4 a 2. Una línea pasa por los puntos “par ordenado 5, 1” y “par ordenado 0, -3”.$

Solución

Localice dos puntos en la gráfica, eligiendo puntos cuyas coordenadas sean números enteros. Utilizaremos (0, −3) y (5, 1).

Comenzando por el punto de la izquierda, (0, −3), esboza un triángulo rectángulo, yendo del primer punto al segundo punto, (5, 1).

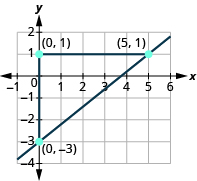
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 6. El eje y va de -4 a 2. Una línea pasa por los puntos “par ordenado 5, 1” y “par ordenado 0, -3”. Dos segmentos de línea forman un triángulo con la línea. Una línea horizontal conecta “par ordenado 0, 1” y “par ordenado 5,1”. Un segmento de línea vertical conecta “par ordenado 0, -3” y “par ordenado 0, 1".$

Cuenta la subida en la pata vertical del triángulo.	El ascenso es de 4 unidades.
Cuenta la carrera en la pierna horizontal.	La carrera es de 5 unidades.
Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Sustituir los valores de la subida y corrida.	$$m =\ dfrac {4} {5} $$

La pendiente de la línea es$\dfrac{4}{5}$.

Observe que la pendiente es positiva ya que la línea se inclina hacia arriba de izquierda a derecha.

Ejercicio$\PageIndex{9}$:

Encuentra la pendiente de la línea:

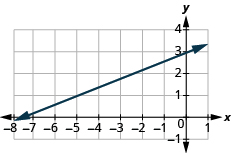
$La gráfica muestra el plano de la coordenada x y. El eje x va de -8 a 1. El eje y va de -1 a 4. Una línea pasa por los puntos “par ordenado -8, 1” y “par ordenado 0, 3”.$

Responder: $\frac{2}{5}$

Ejercicio$\PageIndex{10}$:

Encuentra la pendiente de la línea:

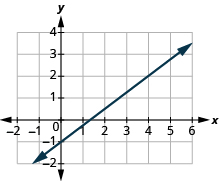
$La gráfica muestra el plano de la coordenada x y. El eje x va de -2 a 6. El eje y va de -2 a 4. Una línea pasa por los puntos “par ordenado 4, 2” y “par ordenado 0, -1”.$

Responder: $\frac{3}{4}$

CÓMO: ENCONTRAR LA PENDIENTE A PARTIR DE

Paso 1. Localice dos puntos en la línea cuyas coordenadas sean números enteros.

Paso 2. Comenzando por el punto de la izquierda, esboza un triángulo rectángulo, yendo del primer punto al segundo punto.

Paso 3. Cuenta la subida y la carrera en las piernas del triángulo.

Paso 4. Toma la proporción de subida para correr para encontrar la pendiente.

\[m = \dfrac{rise}{run}\]

Ejemplo$\PageIndex{6}$:

Encuentra la pendiente de la línea que se muestra:

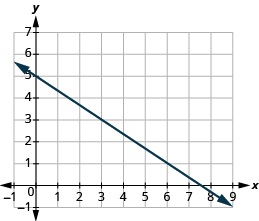
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 9. El eje y va de -1 a 7. Una línea pasa por los puntos “par ordenado 4, 2” y “par ordenado 3, 3”.$

Solución

Localiza dos puntos en la gráfica. Busque puntos con coordenadas que sean números enteros. Podemos elegir cualquier punto, pero usaremos (0, 5) y (3, 3). Comenzando por el punto de la izquierda, esboza un triángulo rectángulo, yendo del primer punto al segundo punto.

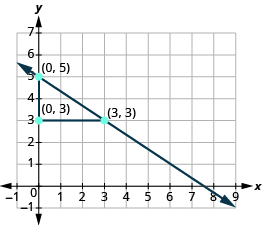
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 9. El eje y va de -1 a 7. Una línea pasa por los puntos “par ordenado 0, 5” y “par ordenado 3, 3”. Dos segmentos de línea forman un triángulo con la línea. Una línea horizontal conecta “par ordenado 0, 3" y “par ordenado 3, 3". Un segmento de línea vertical conecta “par ordenado 0, 3" y “par ordenado 0, 5". Está etiquetado como “subir”.$

Contar la subida — es negativo.	La subida es −2.
Cuenta la carrera.	La carrera es 3.
Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Sustituir los valores de la subida y corrida.	$$m =\ dfrac {-2} {3} $$
Simplificar.	$$m = -\ dfrac {2} {3} $$

La pendiente de la línea es$− \dfrac{2}{3}$.

Observe que la pendiente es negativa ya que la línea se inclina hacia abajo de izquierda a derecha.

¿Y si hubiéramos elegido diferentes puntos? Volvamos a encontrar la pendiente de la línea, esta vez usando diferentes puntos. Usaremos los puntos (−3, 7) y (6, 1).

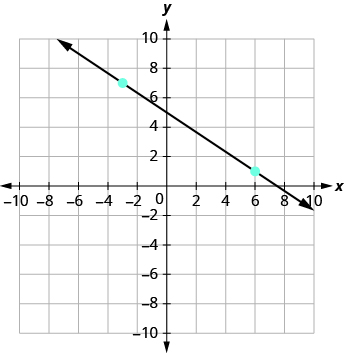
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 9. El eje y va de -1 a 7. Una línea pasa por los puntos “par ordenado 0, 5” y “par ordenado 3, 3”.$

Comenzando en (−3, 7), dibuje un triángulo rectángulo a (6, 1).

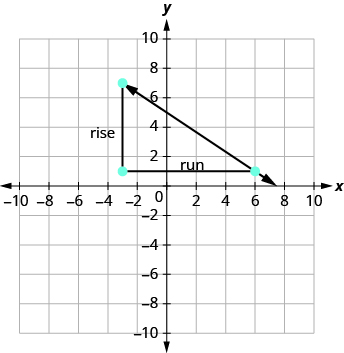
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 9. El eje y va de -1 a 7. Una línea pasa por los puntos “par ordenado 0, 5” y “par ordenado 3, 3”. Dos segmentos de línea forman un triángulo con la línea. Una línea vertical conecta “par ordenado 0, 3" y “par ordenado 3, 3". Un segmento de línea vertical conecta “par ordenado 0, 3" y “par ordenado 0, 5".$

Contar la subida.	La subida es −6.
Cuenta la carrera.	La carrera es 9.
Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Sustituir los valores de la subida y corrida.	$$m =\ dfrac {-6} {9} $$
Simplifica la fracción.	$$m = -\ dfrac {2} {3} $$

La pendiente de la línea es$− \dfrac{2}{3}$.

No importa qué puntos uses, la pendiente de la línea es siempre la misma. ¡La pendiente de una línea es constante!

Ejercicio$\PageIndex{11}$:

Encuentra la pendiente de la línea:

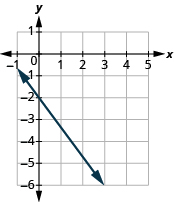
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 5. El eje y va de -6 a 1. Una línea pasa por los puntos “par ordenado 3, -6” y “par ordenado 0, -2”.$

Responder: $-\frac{4}{3}$

Ejercicio$\PageIndex{12}$:

Encuentra la pendiente de la línea:

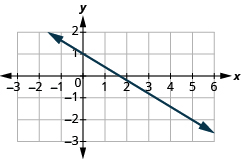
$La gráfica muestra el plano de la coordenada x y. El eje x va de -3 a 6. El eje y va de -3 a 2. Una línea pasa por los puntos “par ordenado 5, -2” y “par ordenado 0, 1”.$

Responder: $-\frac{3}{5}$

Las líneas de los ejemplos anteriores tenían intercepciones y con valores enteros, por lo que fue conveniente usar la intercepción y como uno de los puntos que usamos para encontrar la pendiente. En el siguiente ejemplo, la intercepción y es una fracción. Los cálculos son más fáciles si utilizamos dos puntos con coordenadas enteras.

Ejemplo$\PageIndex{7}$:

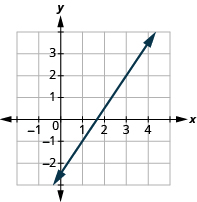
Encuentra la pendiente de la línea que se muestra:

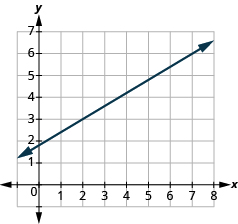
$La gráfica muestra el plano de la coordenada x y. El eje x va de 0 a 7. El eje y va de 0 a 8. Una línea pasa por los puntos “par ordenado 2, 3” y “par ordenado 7, 6”.$

Solución

Localice dos puntos en la gráfica cuyas coordenadas sean números enteros.	(2, 3) y (7, 6)
¿Qué punto está a la izquierda?	(2, 3)

Comenzando en (2, 3), dibuje un ángulo recto a (7, 6) como se muestra a continuación.

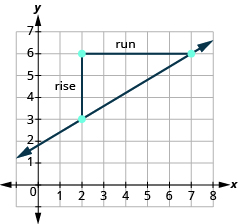
$La gráfica muestra el plano de la coordenada x y. El eje x va de 0 a 7. El eje y va de 0 a 8. Dos puntos sin etiquetar se dibujan en “par ordenado 2, 3” y “par ordenado 7, 6”. Una línea pasa por los puntos. Dos segmentos de línea forman un triángulo con la línea. Una línea vertical conecta “par ordenado 2, 3" y “par ordenado 2, 6". Está etiquetado como “subir”. Un segmento de línea horizontal conecta “par ordenado 2, 6" y “par ordenado 7, 6". Está etiquetado como “correr”.$

Contar la subida.	El ascenso es de 3.
Cuenta la carrera.	La carrera es 5.
Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Sustituir los valores de la subida y corrida.	$$m =\ dfrac {3} {5} $$

La pendiente de la línea es$\dfrac{3}{5}$.

Ejercicio$\PageIndex{13}$:

Encuentra la pendiente de la línea:

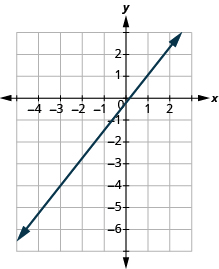
$La gráfica muestra el plano de la coordenada x y. El eje x va de -4 a 2. El eje y va de -5 a 2. Una línea pasa por los puntos “par ordenado -3, -4” y “par ordenado 1, 1”.$

Responder: $\frac{5}{4}$

Ejercicio$\PageIndex{14}$:

Encuentra la pendiente de la línea:

$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 4. El eje y va de -2 a 3. Una línea pasa por los puntos “par ordenado 3, 2” y “par ordenado 1, -1”.$

Responder: $\frac{3}{2}$

Encuentra la Pendiente de Líneas Horizontales y Verticales

¿Recuerdas qué tenían de especial las líneas horizontales y verticales? Sus ecuaciones solo tenían una variable.

línea horizontal y = b; todas las coordenadas y son iguales.
línea vertical x = a; todas las coordenadas x son iguales.

Entonces, ¿cómo encontramos la pendiente de la línea horizontal y = 4? Una aproximación sería graficar la línea horizontal, encontrar dos puntos en ella, y contar la subida y la carrera. Veamos qué pasa en la Figura$\PageIndex{8}$. Usaremos los dos puntos (0, 4) y (3, 4) para contar la subida y la carrera.

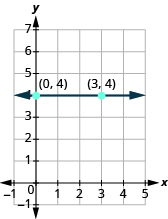
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 5. El eje y va de -1 a 7. Una línea horizontal pasa por los puntos etiquetados “par ordenado 0, 4” y “par ordenado 3, 4”.$

Figura$\PageIndex{8}$

¿Cuál es la subida?	El ascenso es 0.
¿Cuál es la carrera?	La carrera es 3.
¿Cuál es la pendiente?	$$m =\ dfrac {rise} {run}\ tag {11.4.21} $$
	$$m =\ dfrac {0} {3}\ tag {11.4.22} $$
	$$m = 0\ tag {11.4.23} $$

La pendiente de la línea horizontal y = 4 es 0.

Todas las líneas horizontales tienen pendiente 0. Cuando las coordenadas y son las mismas, la subida es 0.

Definición: Pendiente de una línea horizontal

La pendiente de una línea horizontal, y = b, es 0.

Ahora consideraremos una línea vertical, como la línea x = 3, que se muestra en la Figura$\PageIndex{9}$. Usaremos los dos puntos (3, 0) y (3, 2) para contar la subida y la carrera.

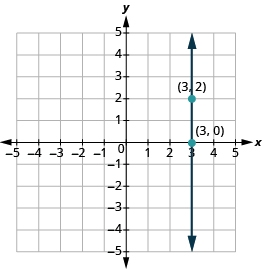
$La gráfica muestra el plano de la coordenada x y. Ambos ejes van de -5 a 5. Una línea vertical pasa por los puntos etiquetados “par ordenado 3, 2” y “par ordenado 3, 0”.$

Figura$\PageIndex{9}$

¿Cuál es la subida?	El ascenso es de 2.
¿Cuál es la carrera?	La carrera es 0.
¿Cuál es la pendiente?	$$m =\ dfrac {rise} {run}\ tag {11.4.24} $$
	$$m =\ dfrac {2} {0}\ tag {11.4.25} $$

Pero no podemos dividir por 0. División por 0 no está definida. Entonces decimos que la pendiente de la línea vertical x = 3 es indefinida. La pendiente de todas las líneas verticales es indefinida, porque la carrera es 0.

Definición: Pendiente de una línea vertical

La pendiente de una línea vertical, x = a, es indefinida.

Ejemplo$\PageIndex{8}$:

Encuentra la pendiente de cada línea: (a) x = 8 (b) y = −5

Solución

(a) x = 8

Esta es una línea vertical, por lo que su pendiente es indefinida.

(b) y = −5

Esta es una línea horizontal, por lo que su pendiente es 0.

Ejercicio$\PageIndex{15}$:

Encuentra la pendiente de la línea: x = −4.

Responder: undefined

Ejercicio$\PageIndex{16}$:

Encuentra la pendiente de la línea: y = 7.

Responder: 0

Guía rápida de las laderas de las líneas

$En la figura se muestran 4 flechas. El primero se eleva de izquierda a derecha con la flecha apuntando hacia arriba. Está etiquetado como “positivo”. El segundo baja de izquierda a derecha con la flecha apuntando hacia abajo. Está etiquetado como “negativo”. El tercero es horizontal con puntas de flecha en ambos extremos. Está etiquetado como “cero”. El último es vertical con puntas de flecha en ambos extremos. Está etiquetado como “indefinido”.$

Usa la Fórmula de Talud para encontrar la Talud de una Línea entre Dos Puntos

A veces necesitamos encontrar la pendiente de una línea entre dos puntos y puede que no tengamos una gráfica para contar la subida y la carrera. Podríamos trazar los puntos en papel de cuadrícula, luego contar la subida y la carrera, pero hay una manera de encontrar la pendiente sin graficar.

Antes de llegar a ella, necesitamos introducir alguna nueva notación algebraica. Hemos visto que un par ordenado (x, y) da las coordenadas de un punto. Pero cuando trabajamos con pendientes, utilizamos dos puntos. ¿Cómo se puede usar el mismo símbolo (x, y) para representar dos puntos diferentes?

Los matemáticos utilizan subíndices para distinguir entre los puntos. Un subíndice es un número pequeño escrito a la derecha de, y un poco más bajo que, una variable.

(x ₁, y ₁) leer x sub 1, y sub 1
(x ₂, y ₂) lectura x sub 2, y sub 2

Utilizaremos (x ₁, y ₁) para identificar el primer punto y (x ₂, y ₂) para identificar el segundo punto. Si tuviéramos más de dos puntos, podríamos usar (x ₃, y ₃), (x ₄, y ₄), y así sucesivamente.

Para ver cómo se relacionan la subida y la carrera con las coordenadas de los dos puntos, echemos otro vistazo a la pendiente de la línea entre los puntos (2, 3) y (7, 6) en la Figura$\PageIndex{10}$.

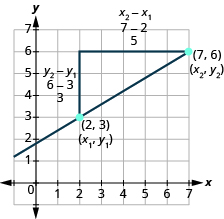
$La gráfica muestra el plano de la coordenada x y. El eje x va de 0 a 7. El eje y va de 0 a 7. Una línea recorre los puntos etiquetados 2, 3 y 7, 6. Un segmento de línea va desde el punto 2, 3 hasta el punto no etiquetado 2, 6. Se etiqueta y sub 2 menos y sub 1, 6 menos 3, 3. Un segmento de línea va desde el punto 7, 6 hasta el punto no etiquetado 2, 6. Es os etiquetado x sub 2 menos x sub 1, 7 menos 2, 5.$

Figura$\PageIndex{10}$

Ya que tenemos dos puntos, usaremos notación subíndice.

\[\begin{split} x_{1}, y_{1} \qquad &x_{2}, y_{2} \\ (2, 3) \qquad &(7, 6) \end{split}\]

En la gráfica, contamos la subida de 3. La subida también se puede encontrar restando las coordenadas y de los puntos.

\[\begin{split} y_{2} &- y_{1} \\ 6 &- 3 \\ &\; 3 \end{split}\]

Contamos una corrida de 5. La carrera también se puede encontrar restando las coordenadas x.

\[\begin{split} x_{2} &- x_{1} \\ 7 &- 2 \\ &\; 5 \end{split}\]

Sabemos	$$m =\ dfrac {rise} {run}\ tag {11.4.26} $$
Entonces	$$m =\ dfrac {3} {5}\ tag {11.4.27} $$
Reescribimos la subida y corremos poniendo en las coordenadas.	$$m =\ dfrac {6 - 3} {7 - 2}\ tag {11.4.28} $$
Pero 6 es la coordenada y del segundo punto, y ₂ y 3 es la coordenada y del primer punto y ₁. Así podemos reescribir la subida usando notación subíndice.	$$m =\ dfrac {y_ {2} - y_ {1}} {7 - 2}\ tag {11.4.29} $$
También 7 es la coordenada x del segundo punto, x ₂ y 2 es la coordenada x del primer punto x ₂. Así que reescribimos la ejecución usando notación de subíndices.	$$m =\ dfrac {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ tag {11.4.30} $$

Hemos demostrado que m =$\dfrac{y_{2} − y_{1}}{x_{2} − x_{1}}$ es realmente otra versión de m =$\dfrac{rise}{run}$. Podemos usar esta fórmula para encontrar la pendiente de una línea cuando tenemos dos puntos en la línea.

Definición: Fórmula de talud

La pendiente de la línea entre dos puntos (x ₁, y ₁) y (x ₂, y ₂) es

\[m = \dfrac{y_{2} - y_{1}}{x_{2} - x_{1}} \tag{11.4.31}\]

Dígase la fórmula para ayudarle a recordarla:

La pendiente es y del segundo punto menos y del primer punto

sobre

x del segundo punto menos x del primer punto.

Ejemplo$\PageIndex{9}$:

Encuentra la pendiente de la línea entre los puntos (1, 2) y (4, 5).

Solución

Llamaremos al (1, 2) punto #1 y (4, 5) punto #2.	$$\ begin {split} x_ {1}, y_ {1}\ qquad &x_ {2}, y_ {2}\\ (1, 2)\ qquad & (4, 5)\ end {split} $$
Utilice la fórmula de pendiente.	$$m =\ dfrac {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ tag {11.4.32} $$
Sustituya los valores en la fórmula de pendiente:
y del segundo punto menos y del primer punto	$$m =\ dfrac {5 - 2} {x_ {2} - x_ {1}}\ tag {11.4.33} $$
x del segundo punto menos x del primer punto	$$m =\ dfrac {5 - 2} {4 - 1}\ tag {11.4.34} $$
Simplifica el numerador y el denominador.	$$m =\ dfrac {3} {3}\ tag {11.4.35} $$
	m = 1

Confirmemos esto contando la pendiente en la gráfica.

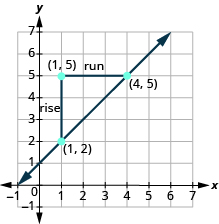
$La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 7. El eje y va de -1 a 7. Dos puntos etiquetados se dibujan en “par ordenado 1, 2” y “par ordenado 4, 5". Una línea pasa por los puntos. Dos segmentos de línea forman un triángulo con la línea. Una línea vertical conecta “par ordenado 1, 2” y “par ordenado 1, 5”. Está etiquetado como “subir”. Un segmento de línea horizontal conecta “par ordenado 1, 5” y “par ordenado 4, 5". Está etiquetado como “correr”.$

El ascenso es de 3 y la carrera es de 3, entonces

\[\begin{split} m &= \dfrac{rise}{run} \\ m &= \dfrac{3}{3} \\ m &= 1 \end{split}\]

Ejercicio$\PageIndex{17}$:

Encuentra la pendiente de la línea a través de los puntos dados: (8, 5) y (6, 3).

Responder: 1

Ejercicio$\PageIndex{18}$:

Encuentra la pendiente de la línea a través de los puntos dados: (1, 5) y (5, 9).

Responder: 1

¿Cómo sabemos a qué punto llamar #1 y cuál llamar #2? Volvamos a encontrar la pendiente, esta vez cambiando los nombres de los puntos para ver qué pasa. Ya que ahora vamos a estar contando la carrera de derecha a izquierda, será negativa.

Llamaremos al (4, 5) punto #1 y (1, 2) punto #2.	$$\ begin {split} x_ {1}, y_ {1}\ qquad &x_ {2}, y_ {2}\\ (4, 5)\ qquad & (1, 2)\ end {split} $$
Utilice la fórmula de pendiente.	$$m =\ dfrac {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ tag {11.4.36} $$
Sustituya los valores en la fórmula de pendiente:
y del segundo punto menos y del primer punto	$$m =\ dfrac {2 - 5} {x_ {2} - x_ {1}}\ tag {11.4.37} $$
x del segundo punto menos x del primer punto	$$m =\ dfrac {2 - 5} {1 - 4}\ tag {11.4.38} $$
Simplifica el numerador y el denominador.	$$m =\ dfrac {-3} {-3}\ tag {11.4.39} $$
	m = 1

La pendiente es la misma sin importar en qué orden usemos los puntos.

Ejemplo$\PageIndex{10}$:

Encuentra la pendiente de la línea a través de los puntos (−2, −3) y (−7, 4).

Solución

Llamaremos (−2, −3) punto #1 y (−7, 4) punto #2.	$$\ begin {split} x_ {1}, y_ {1}\ qquad &x_ {2}, y_ {2}\\ (-2, -3)\ qquad & (-7, 4)\ end {split} $$
Utilice la fórmula de pendiente.	$$m =\ dfrac {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ tag {11.4.40} $$
Sustituir los valores.
y del segundo punto menos y del primer punto	$$m =\ dfrac {4 - (-3)} {x_ {2} - x_ {1}}\ tag {11.4.41} $$
x del segundo punto menos x del primer punto	$$m =\ dfrac {4 - (-3)} {-7 - (-2)}\ tag {11.4.42} $$
Simplificar.	$$m =\ dfrac {7} {-5}\ tag {11.4.43} $$
	m =$- \dfrac{7}{5}$

Confirmemos esto en la gráfica que se muestra.

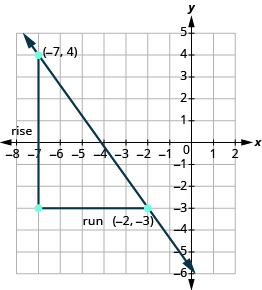
$La gráfica muestra el plano de la coordenada x y. El eje x va de -8 a 2. El eje y va de -6 a 5. Dos puntos sin etiquetar se dibujan en “par ordenado -7, 4” y “par ordenado -2, -3”. Una línea pasa por los puntos. Dos segmentos de línea forman un triángulo con la línea. Una línea vertical conecta “par ordenado -7, 4” y “par ordenado -7, -3”. Está etiquetado como “subir”. Un segmento de línea horizontal conecta “par ordenado -7, -3” y “par ordenado -2, -3”. Está etiquetado como “correr”.$

\[\begin{split} m &= \dfrac{rise}{run} \\ m &= \dfrac{-7}{5} \\ m &= - \dfrac{7}{5} \end{split}\]

Ejercicio$\PageIndex{19}$:

Encuentra la pendiente de la línea a través del par de puntos: (−3, 4) y (2, −1).

Responder: -1

Ejercicio$\PageIndex{20}$:

Encuentra la pendiente de la línea a través del par de puntos: (−2, 6) y (−3, −4).

Responder: 10

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

Search

Definición: Pendiente de una línea

Ejemplo\(\PageIndex{1}\):

Ejercicio\(\PageIndex{1}\):

Ejercicio\(\PageIndex{2}\):

Ejemplo\(\PageIndex{2}\):

Ejercicio\(\PageIndex{3}\):

Ejercicio\(\PageIndex{4}\):

Ejemplo\(\PageIndex{3}\):

Ejercicio\(\PageIndex{5}\):

Ejercicio\(\PageIndex{6}\):

Ejemplo\(\PageIndex{4}\):

Ejercicio\(\PageIndex{7}\):

Ejercicio\(\PageIndex{8}\):

Ejemplo\(\PageIndex{5}\):

Ejercicio\(\PageIndex{9}\):

Ejercicio\(\PageIndex{10}\):

CÓMO: ENCONTRAR LA PENDIENTE A PARTIR DE

Ejemplo\(\PageIndex{6}\):

Ejercicio\(\PageIndex{11}\):

Ejercicio\(\PageIndex{12}\):

Ejemplo\(\PageIndex{7}\):

Ejercicio\(\PageIndex{13}\):

Ejercicio\(\PageIndex{14}\):

Definición: Pendiente de una línea horizontal

Definición: Pendiente de una línea vertical

Ejemplo\(\PageIndex{8}\):

Ejercicio\(\PageIndex{15}\):

Ejercicio\(\PageIndex{16}\):

Guía rápida de las laderas de las líneas

Definición: Fórmula de talud

Ejemplo\(\PageIndex{9}\):

Ejercicio\(\PageIndex{17}\):

Ejercicio\(\PageIndex{18}\):

Ejemplo\(\PageIndex{10}\):

Ejercicio\(\PageIndex{19}\):

Ejercicio\(\PageIndex{20}\):

Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Reemplazar m con\(\dfrac{1}{2}\).	$$\ dfrac {1} {2} =\ dfrac {subida} {correr} $$

Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} $$
Reemplazar m con\(− \dfrac{1}{4}\).	$$-\ dfrac {1} {4} =\ dfrac {subida} {correr} $$