11.6: Graficar con intercepciones (Parte 2)
- Page ID
- 114235
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Elija el método más conveniente para graficar una línea
Si bien podríamos graficar cualquier ecuación lineal trazando puntos, puede que no siempre sea el método más conveniente. Esta tabla muestra seis de las ecuaciones que hemos graficado en este capítulo, y los métodos que utilizamos para graficarlas.
| Ecuación | Método | |
|---|---|---|
| #1 | y = 2x + 1 | Puntos de trazado |
| #2 | y =\(\dfrac{1}{2}\) x + 3 | Puntos de trazado |
| #3 | x = −7 | Línea vertical |
| #4 | y = 4 | Línea horizontal |
| #5 | 2x + y = 6 | Intercepta |
| #6 | 4x − 3 años = 12 | Intercepta |
¿Qué tiene la forma de ecuación que puede ayudarnos a elegir el método más conveniente para graficar su línea?
Observe que en las ecuaciones #1 y #2, y está aislado en un lado de la ecuación, y su coeficiente es 1. Encontramos puntos sustituyendo valores por x en el lado derecho de la ecuación y luego simplificando para obtener los valores y correspondientes.
Las ecuaciones #3 y #4 tienen cada una solo una variable. Recuerde, en este tipo de ecuaciones el valor de esa variable es constante; no depende del valor de la otra variable. Las ecuaciones de esta forma tienen gráficas que son líneas verticales u horizontales.
En las ecuaciones #5 y #6, tanto x como y están en el mismo lado de la ecuación. Estas dos ecuaciones son de la forma Ax + By = C. Sustituimos y = 0 y x = 0 para encontrar las intercepciones x e y, a continuación, encontramos un tercer punto eligiendo un valor para x o y.
Esto lleva a la siguiente estrategia para elegir el método más conveniente para graficar una línea.
Paso 1. Si la ecuación tiene sólo una variable. Es una línea vertical u horizontal.
- x = a es una línea vertical que pasa por el eje x en a.
- y = b es una línea horizontal que pasa por el eje y en b.
Paso 2. Si y está aislado en un lado de la ecuación. Gráfica trazando puntos.
- Elija tres valores cualesquiera para x y luego resuelva para los valores y- correspondientes.
Paso 3. Si la ecuación es de la forma Ax + By = C, encuentra las intercepciones.
- Encuentra las intercepciones x e y y luego un tercer punto.
Identificar el método más conveniente para graficar cada línea: (a) y = −3 (b) 4x−6y = 12 (c) x = 2 (d) y = 2 5 x−1
Solución
(a) y = −3
Esta ecuación tiene una sola variable, y. Su gráfica es una línea horizontal que cruza el eje y en −3.
(b) 4x−6y = 12
Esta ecuación es de la forma Ax + By = C. Encuentra las intercepciones y un punto más.
(c) x = 2
Sólo hay una variable, x. La gráfica es una línea vertical que cruza el eje x en 2.
(d) y =\(\dfrac{2}{5}\) x−1
Dado que y está aislado en el lado izquierdo de la ecuación, será más fácil graficar esta línea trazando tres puntos.
Identificar el método más conveniente para graficar cada línea: (a) 3x + 2y = 12 (b) y = 4 (c) y =\(\dfrac{1}{5}\) x−4 (d) x = −7
- Contestar a
-
intercepta
- Respuesta b
-
línea horizontal
- Respuesta c
-
trazando puntos
- Respuesta d
-
línea vertical
Identificar el método más conveniente para graficar cada línea: (a) x = 6 (b) y =\(− \dfrac{3}{4}\) x + 1 (c) y = −8 (d) 4x−3y = −1
- Contestar a
-
línea vertical
- Respuesta b
-
trazando puntos
- Respuesta c
-
línea horizontal
- Respuesta d
-
intercepta
La práctica hace la perfección
Identificar las Intercepciones en una Gráfica
En los siguientes ejercicios, encuentra las intercepciones x e y.
Encuentra las intercepciones x e y a partir de una ecuación de una línea
En los siguientes ejercicios, encuentra las intercepciones.
- x + y = 4
- x + y = 3
- x + y = −2
- x + y = −5
- x − y = 5
- x − y = 1
- x − y = −3
- x − y = −4
- x + 2y = 8
- x + 2y = 10
- 3x + y = 6
- 3x + y = 9
- x−3y = 12
- x−2y = 8
- 4x − y = 8
- 5x − y = 5
- 2x + 5 años = 10
- 2x + 3 años = 6
- 3x−2y = 12
- 3x−5y = 30
- y =\(\dfrac{1}{3}\) x−1
- y =\(\dfrac{1}{4}\) x−1
- y =\(\dfrac{1}{5}\) x + 2
- y =\(\dfrac{1}{3}\) x + 4
- y = 3x
- y = −2x
- y = −4x
- y = 5x
Graficar una línea usando las intercepciones
En los siguientes ejercicios, grafica usando las intercepciones.
- −x + 5y = 10
- −x + 4y = 8
- x + 2y = 4
- x + 2y = 6
- x + y = 2
- x + y = 5
- x + y = −3
- x + y = −1
- x − y = 1
- x − y = 2
- x − y = −4
- x − y = −3
- 4x + y = 4
- 3x + y = 3
- 3x − y = −6
- 2x − y = −8
- 2x + 4 años = 12
- 3x + 2 años = 12
- 3x−2y = 6
- 5x−2y = 10
- 2x−5y = −20
- 3x−4y = −12
- y = −2x
- y = −4x
- y = x
- y = 3x
Elija el método más conveniente para graficar una línea
En los siguientes ejercicios, identifica el método más conveniente para graficar cada línea.
- x = 2
- y = 4
- y = 5
- x = −3
- y = −3x + 4
- y = −5x + 2
- x − y = 5
- x − y = 1
- y =\(\dfrac{2}{3}\) x−1
- y =\(\dfrac{4}{5}\) x−3
- y = −3
- y = −1
- 3x−2y = −12
- 2x−5y = −10
- y =\(− \dfrac{1}{4}\) x + 3
- y =\(− \dfrac{1}{3}\) x + 5
Matemáticas cotidianas
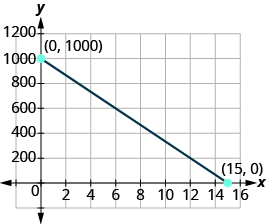
- Viaje por carretera Damien está conduciendo de Chicago a Denver, a una distancia de 1,000 millas. El eje x de la gráfica a continuación muestra el tiempo en horas desde que Damien salió de Chicago. El eje y representa la distancia que le queda para conducir.
- Encuentra las intercepciones x e y.
- Explique qué significan las intercepciones x e y para Damien.
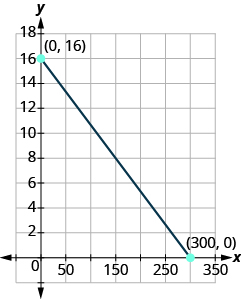
- Viaje por carretera Ozzie llenó el tanque de gasolina de su camioneta y se fue de viaje por carretera. El eje x en la gráfica muestra el número de millas que Ozzie condujo desde que se llenó. El eje y representa el número de galones de gas en el tanque de gasolina del camión.
- Encuentra las intercepciones x e y.
- Explique qué significan las intercepciones x e y para Ozzie.
Ejercicios de escritura
- ¿Cómo encuentra la intercepción x de la gráfica de 3x−2y = 6?
- ¿Cómo encuentra la intercepción y de la gráfica de 5x − y = 10?
- ¿Prefiere graficar la ecuación 4x + y = −4 trazando puntos o intercepciones? ¿Por qué?
- ¿Prefiere graficar la ecuación y =\(\dfrac{2}{3}\) x − 2 trazando puntos o intercepciones? ¿Por qué?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
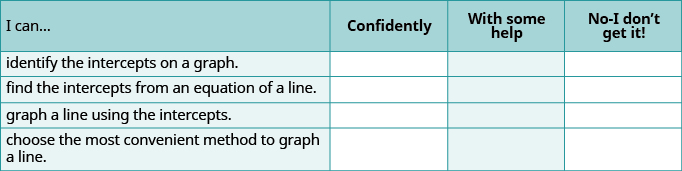
(b) ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?