1.1.5: Movimientos de coordenadas

Última actualización
Guardar como PDF

Page ID: 118684

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Transformemos algunas figuras y veamos qué pasa con las coordenadas de los puntos.

Ejercicio$\PageIndex{1}$: Translating Coordinates

Selecciona todas las traducciones que llevan Triángulo T a Triángulo U. Puede haber más de una respuesta correcta.

Traducir$(-3,0)$ a$(1,2)$.
Traducir$(2,1)$ a$(-2,-1)$.
Traducir$(-4,-3)$ a$(0,-1)$.
Traducir$(1,2)$ a$(2,1)$.

Ejercicio$\PageIndex{2}$: Reflecting Points on the Coordinate Plane

Se trazan cinco puntos en el plano de coordenadas.
1. Usando la herramienta Pluma o la herramienta Texto, etiquete cada una con sus coordenadas.
2. Usando el$x$ eje -como línea de reflexión, trazar la imagen de cada punto.
3. Etiquetar la imagen de cada punto con sus coordenadas.
4. Incluya una etiqueta usando una letra. Por ejemplo, se$A$ debe etiquetar la imagen de punto$A'$.
Si el punto$(13,10)$ se reflejara usando el$x$ eje -como línea de reflexión, ¿cuáles serían las coordenadas de la imagen? ¿Y qué pasa$(13,-20)$? $(13,570)$? Explique cómo sabe.
El punto$R$ tiene coordenadas$(3,2)$.
1. Sin graficar, predecir las coordenadas de la imagen de punto$R$ si el punto$R$ se reflejó usando el$y$ eje -como línea de reflexión.
2. Comprueba tu respuesta encontrando la imagen de$R$ en la gráfica.
  
  $clipboard_e93946b30837001f90406e33fb9d2ac0d.png$
  Figura$\PageIndex{2}$
3. Etiquetar la imagen del punto$R$ como$R'$.
4. ¿De qué son las coordenadas$R'$?
Supongamos que refleja un punto usando el$y$ eje -como línea de reflexión. ¿Cómo describirías su imagen?

Ejercicio$\PageIndex{3}$: Transformations of a Segment

El applet tiene instrucciones para las primeras 3 preguntas integradas en él. Mueve el control deslizante marcado como “pregunta” cuando estés listo para responder a la siguiente. Haga una pausa antes de usar el applet para mostrar la transformación descrita en cada pregunta para predecir dónde estarán las nuevas coordenadas.

Aplicar cada una de las siguientes transformaciones al segmento$AB$. Utilice la herramienta Pluma para registrar las coordenadas.

Gire el segmento$AB$ 90 grados en sentido antihorario alrededor del centro$B$ moviendo el deslizador marcado 0 grados. Se nombra$A$ la imagen de$C$. ¿De qué son las coordenadas$C$?
Gire el segmento$AB$ 90 grados en sentido antihorario alrededor del centro$A$ moviendo el deslizador marcado 0 grados. Se nombra$B$ la imagen de$D$. ¿De qué son las coordenadas$D$?
Gire el segmento$AB$ 90 grados en sentido horario$(0,0)$ moviendo el deslizador marcado 0 grados. Se nombra la imagen de$E$ y$A$ se nombra la imagen de$B$$F$. ¿Cuáles son las coordenadas de$E$ y$F$?
Compare las dos rotaciones de 90 grados en sentido antihorario del segmento$AB$. ¿Qué pasa con las imágenes de estas rotaciones? ¿Qué es diferente?

¿Estás listo para más?

Supongamos$EF$ y$GH$ son segmentos de línea de la misma longitud. Describir una secuencia de transformaciones que se traslada$EF$ a$GH$.

Resumen

Podemos usar coordenadas para describir puntos y encontrar patrones en las coordenadas de puntos transformados.

Podemos describir una traducción expresándola como una secuencia de traducciones horizontales y verticales. Por ejemplo, el segmento$AB$ se traduce a la derecha 3 y hacia abajo 2.

Figura$\PageIndex{3}$: Cuadrilátero en un plano de coordenadas. Escala del eje horizontal negativo 3 a 5 por 1's. Escala del eje vertical negativo 2 a 3 por 1's. Cuadrilátero A B B primo A primo tiene las coordenadas A (negativo 2 coma 1), B (1 coma 2), B primo (4 coma 0) y A primo (1 coma negativo 1).

Reflejar un punto a través de un eje cambia el signo de una coordenada. Por ejemplo, al reflejar el punto$A$ cuyas coordenadas están$(2,-1)$ a través del$x$ eje -se cambia el signo de la$y$ coordenada, haciendo de su imagen el punto$A'$ cuyas coordenadas son$(2,1)$. Reflejar el punto$A$ a través$y$ del eje cambia el signo de la$x$ coordenada, haciendo de la imagen el punto$A"$ cuyas coordenadas son$(-2,-1)$.

Figura$\PageIndex{4}$: 3 puntos en un plano de coordenadas. Escala del eje horizontal negativo 3 a 5 por 1's. Escala del eje vertical negativo 2 a 2 por 1's. Los puntos tienen estas coordenadas: A (2 coma negativa 1), A primo (2 coma 1) y A doble primo (negativo 2 coma negativo 1).

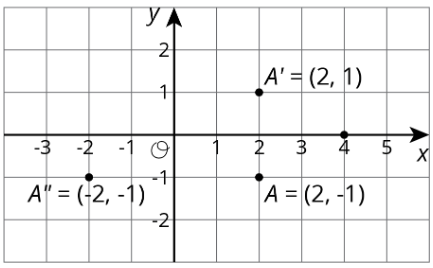
Las reflexiones a través de otras líneas son más complejas de describir.

Aún no tenemos las herramientas para describir las rotaciones en términos de coordenadas en general. Aquí hay un ejemplo de una$90^{\circ}$ rotación con centro$(0,0)$ en sentido contrario a las agujas del reloj.

Figura$\PageIndex{5}$: Segmento A B girado en un plano de coordenadas, origen O. Escala del eje horizontal negativa 4 a 4 por 1. Escala del eje vertical negativa 2 a 4 por 1's. Los segmentos tienen estas coordenadas: A (0 coma 0), B (2 coma 3) y B prima (negativa 3 coma 2). Ángulo B A B primo es un ángulo recto.

$A$El punto tiene coordenadas$(0,0)$. $AB$El segmento se giró en$90^{\circ}$ sentido antihorario alrededor$A$. Punto$B$ con coordenadas$(2,3)$ gira a punto$B'$ cuyas coordenadas son$(-3,2)$.

Entradas en el glosario

Definición: en sentido horario

En sentido horario significa girar en la misma dirección que las manecillas de un reloj. La parte superior gira a la derecha. Este diagrama muestra la Figura A girada en sentido horario para hacer la Figura B.

Definición: Plano de coordenadas

El plano de coordenadas es un sistema para indicar dónde están los puntos. Por ejemplo. punto$R$ se encuentra en$(3,2)$ en el plano de coordenadas, ya que es de tres unidades a la derecha y dos unidades hacia arriba.

Definición: En sentido antihorario

En sentido antihorario significa girar opuesto a la forma en que giran las manecillas de un reloj. La parte superior gira a la izquierda.

Este diagrama muestra la Figura A girada en sentido antihorario para hacer la Figura B.

Definición: Imagen

Una imagen es el resultado de traducciones, rotaciones y reflexiones sobre un objeto. Cada parte del objeto original se mueve de la misma manera para coincidir con una parte de la imagen.

En este diagrama, el triángulo se$ABC$ ha traducido hacia arriba y hacia la derecha para hacer triángulo$DEF$. Triángulo$DEF$ es la imagen del triángulo original$ABC$.

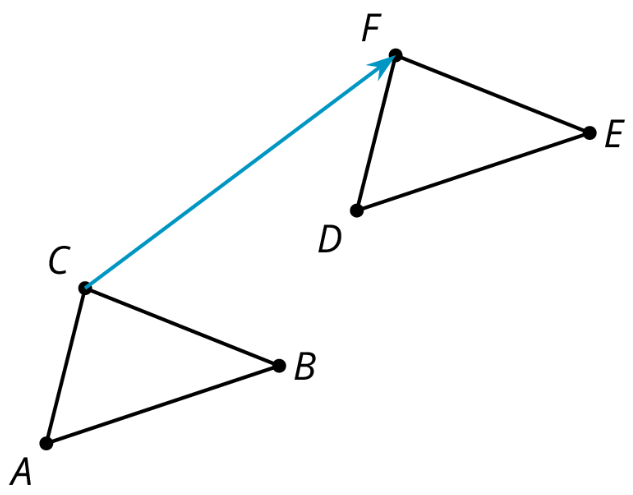
Definición: Reflexión

Una reflexión a través de una línea mueve cada punto de una figura a un punto directamente en el lado opuesto de la línea. El nuevo punto está a la misma distancia de la línea que estaba en la figura original.

Este diagrama muestra un reflejo de A sobre línea$l$ que hace que la imagen especular B.

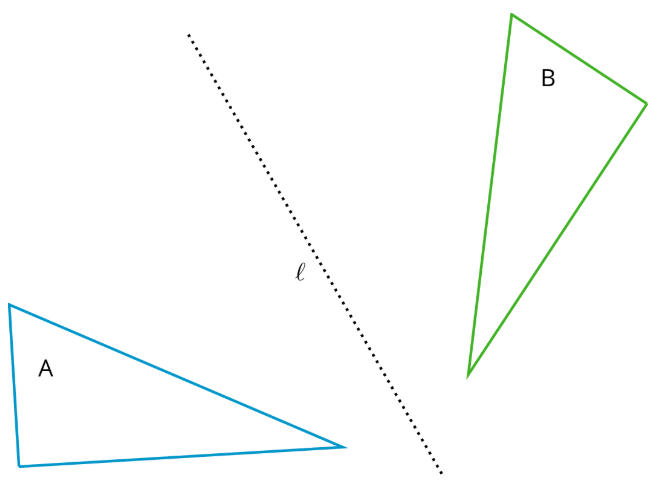
Definición: Rotación

Una rotación mueve cada punto de una figura alrededor de un centro en un ángulo dado en una dirección específica.

Este diagrama muestra el Triángulo A girado alrededor del centro$O$ 55 grados en sentido horario para obtener el Triángulo B.

Definición: Secuencia de Transformaciones

Una secuencia de transformaciones es un conjunto de traslaciones, rotaciones, reflexiones y dilataciones sobre una figura. Las transformaciones se realizan en un orden dado.

Este diagrama muestra una secuencia de transformaciones para mover la Figura A a la Figura C.

Primero, A se traduce a la derecha para hacer B. A continuación, B se refleja a través de la línea$l$ para hacer C.

Definición: Transformación

Una transformación es una traslación, rotación, reflexión o dilatación, o una combinación de estas.

Definición: Traducción

Una traslación mueve cada punto de una figura una distancia dada en una dirección dada.

Este diagrama muestra una traslación de la Figura A a la Figura B usando la dirección y la distancia dadas por la flecha.

Definición: Vertex

Un vértice es un punto donde dos o más aristas se encuentran. Cuando tenemos más de un vértice, los llamamos vértices.

Los vértices en este polígono están etiquetados$A, B, C, D,$ y$E$.

Practica

Ejercicio$\PageIndex{4}$

1. Aquí hay algunos puntos.

Figura$\PageIndex{15}$: Puntos,$A, B$ y$C$ en un plano coordenado, origen$O$. Escala del eje horizontal negativo 10 a 8 por 1's. Escala del eje vertical negativo 4 a 6 por 1's. Las coordenadas de los puntos son$A$ (negativo 6 coma 5),$B$ (3 coma 2) y$C$ (negativo 1 coma 0).

¿Cuáles son las coordenadas de$A, B$, y$C$ después de una traducción a la derecha por 4 unidades y hasta 1 unidad? Trazar estos puntos en la cuadrícula, y etiquetarlos$A'$,$B'$ y$C'$.

2. Aquí hay algunos puntos.

Figura$\PageIndex{16}$: Puntos$D$,$E$ y$F$ en un plano coordenado, origen$O$. Escala del eje horizontal negativo 5 a 5 por 1's. Escala del eje vertical negativo 2 a 3 por 1's. Las coordenadas de los puntos son$D$ (negativo 3 coma 3),$E$ (5 coma 0) y$F$ (2 coma negativa 2).

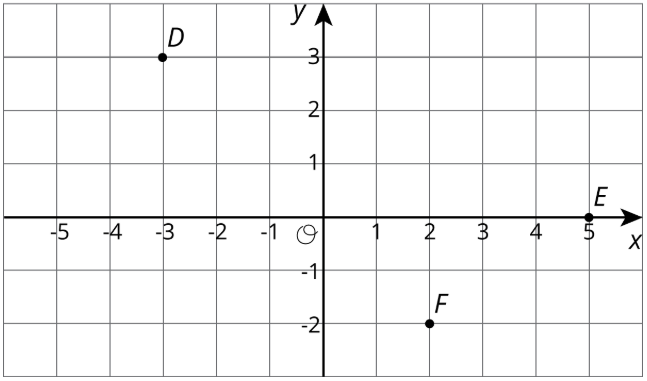
¿Cuáles son las coordenadas de$D$$E$, y$F$ después de una reflexión sobre el eje? Trazar estos puntos en la cuadrícula, y etiquetarlos$D'$,$E'$ y$F'$.

3. Aquí hay algunos puntos.

Figura$\PageIndex{17}$: Puntos$G, H$ y$I$ en un plano de coordenadas, origen O. Escala del eje horizontal negativo 5 a 5 por 1's. Escala del eje vertical negativo 3 a 5 por 1's. Las coordenadas de los puntos son$G$ (negativo 1 coma 3),$H$ (negativo 4 coma 0) y$I$ (3 coma negativo 2).

¿Cuáles son las coordenadas de$G$,$H$, y$I$ después de una rotación alrededor$(0,0)$ de 90 grados en sentido horario? Trazar estos puntos en la cuadrícula, y etiquetarlos$G'$,$H'$ y$I'$.

Ejercicio$\PageIndex{5}$

Describir una secuencia de transformaciones que lleva el trapezoide A al trapecio B.

Figura$\PageIndex{18}$: El cuadrilátero A y su imagen cuadrilátero B son trapezoides. El cuadrilátero A está en la esquina inferior derecha, las bases son verticales y la base más pequeña está a la derecha. El cuadrilátero B está en la esquina superior izquierda, las bases están inclinadas hacia abajo hasta la esquina opuesta y la base más pequeña está en la parte superior.

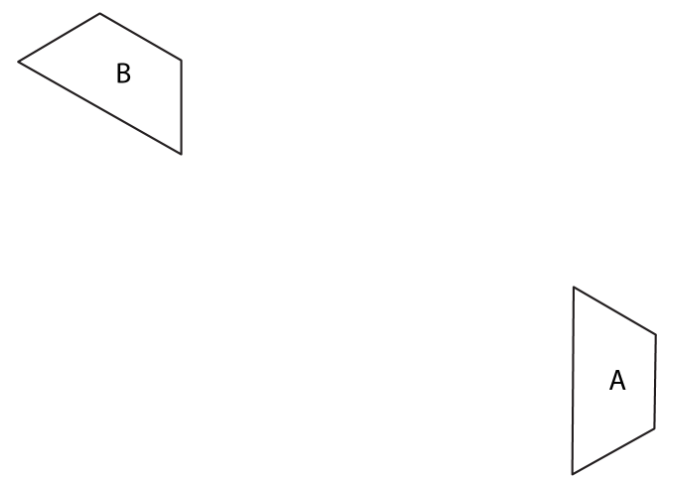
(De la Unidad 1.1.4)

Ejercicio$\PageIndex{6}$

Reflejar polígono$P$ usando línea$l$.

Figura$\PageIndex{19}$: Polígono P y línea discontinua$l$ en una cuadrícula. Dejar (0 coma 0) ser la esquina inferior izquierda. Entonces las coordenadas del polígono P son (1 coma 2), (2 coma 3), (4 coma 3), (3 coma 2), (3 coma 1) y (2 coma 1). Línea$l$ es la línea vertical$x$ = 4 punto 5.

(De la Unidad 1.1.3)

Search

Text Color

Text Size

Margin Size

Font Type