1.2.3: Movimientos en Paralelo
- Page ID
- 118673
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Transformemos algunas líneas.
Ejercicio\(\PageIndex{1}\): Line Moves
Para cada diagrama, describa una traslación, rotación o reflexión que toma línea\(l\) a línea\(l'\). Después trazar y etiquetar\(A'\) y\(B'\), las imágenes de\(A\) y\(B\).
1.
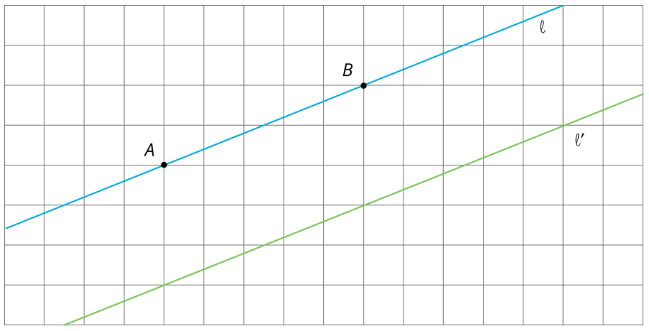
2.
Ejercicio\(\PageIndex{2}\): Parallel Lines
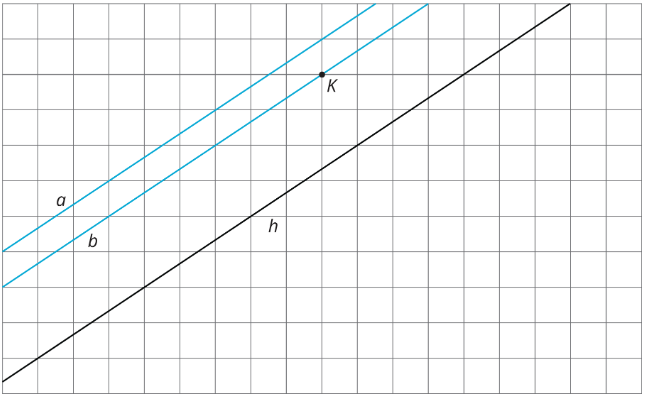
Use un trozo de papel de calco para trazar líneas\(a\)\(b\) y señalar\(K\). Luego usa ese papel de calco para dibujar las imágenes de las líneas bajo las tres transformaciones diferentes enumeradas.
A medida que realice cada transformación, piense en la pregunta:
¿Cuál es la imagen de dos líneas paralelas bajo una transformación rígida?
- Traduce líneas\(a\) y\(b\) 3 unidades hacia arriba y 2 unidades a la derecha.
- ¿Qué nota sobre los cambios que se producen en las líneas\(a\) y\(b\) después de la traducción?
- ¿Qué es lo mismo en el original y en la imagen?
- Girar las líneas\(a\) y\(b\) en sentido antihorario 180 grados usando\(K\) como centro de rotación.
- ¿Qué nota sobre los cambios que se producen en las líneas\(a\) y\(b\) después de la rotación?
- ¿Qué es lo mismo en el original y en la imagen?
- Refleja líneas\(a\) y\(b\) a través de línea\(h\).
- ¿Qué nota sobre los cambios que se producen en las líneas\(a\) y\(b\) después de la reflexión?
- ¿Qué es lo mismo en el original y en la imagen?
¿Estás listo para más?
Cuando gira dos líneas paralelas, a veces las dos líneas originales se cruzan con sus imágenes y forman un cuadrilátero. ¿Qué es lo más específico que puedes decir de este cuadrilátero? ¿Puede ser un cuadrado? ¿Un rombo? ¿Un rectángulo que no es cuadrado? Explica tu razonamiento.
Ejercicio\(\PageIndex{3}\): Let's Do Some 180's
- El diagrama muestra una línea con puntos etiquetados\(A\),\(C\),\(D\), y\(B\).
- En el diagrama, dibuja la imagen de la línea y los puntos\(A\),\(C\), y\(B\) después de que la línea haya sido girada 180 grados alrededor del punto\(D\).
- Etiquetar las imágenes de los puntos\(A'\),\(B'\), y\(C'\).
- ¿Cuál es el orden de los siete puntos? Explica o muestra tu razonamiento.
2. El diagrama muestra una línea con puntos\(A\) y\(C\) en la línea y un segmento\(AD\) donde no\(D\) está en la línea.
- Gire la figura 180 grados alrededor del punto\(C\). Etiquetar la imagen de\(A\) como\(A'\) y la imagen de\(D\) como\(D'\).
- ¿Qué sabes de la relación entre ángulo\(CAD\) y ángulo\(C'A'D'\)? Explica o muestra tu razonamiento.
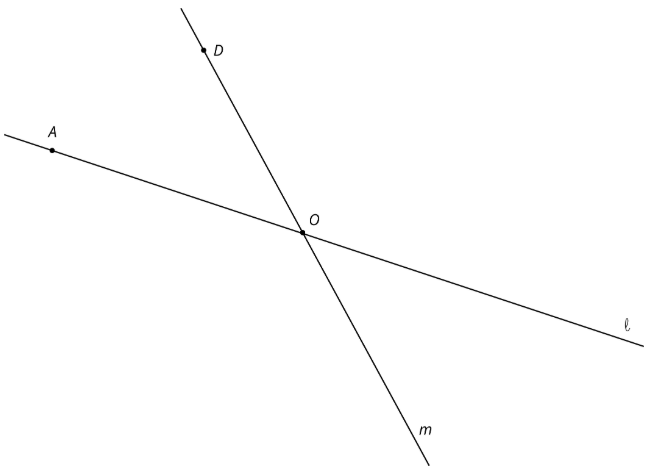
3. El diagrama muestra dos líneas\(l\) y\(m\) que se cruzan en un punto\(O\) con\(A\) el punto encendido\(l\) y el punto\(D\) encendido\(m\).
- Gire la figura 180 grados alrededor\(O\). Etiquetar la imagen de\(A\) como\(A'\) y la imagen de\(D\) como\(D'\).
- ¿Qué sabes de la relación entre los ángulos en la figura? Explica o muestra tu razonamiento.
Resumen
Las transformaciones rígidas tienen las siguientes propiedades:
- Una transformación rígida de una línea es una línea.
- Una transformación rígida de dos líneas paralelas da como resultado dos líneas paralelas que están a la misma distancia que las dos líneas originales.
- A veces, una transformación rígida toma una línea hacia sí misma. Por ejemplo:
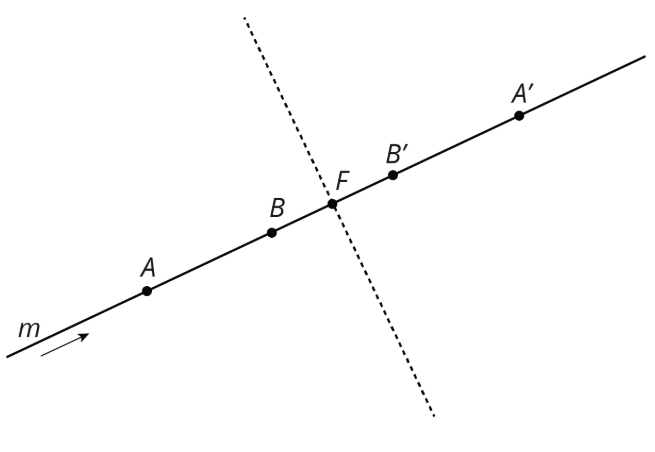
- Una traslación paralela a la línea. La flecha muestra una traducción de línea\(m\) que se llevará\(m\) a sí misma.
- Una rotación\(180^{\circ}\) alrededor de cualquier punto de la línea. Una\(180^{\circ}\) rotación de la línea\(m\) alrededor del punto\(F\) se llevará\(m\) a sí misma.
- Reflejo a través de cualquier línea perpendicular a la línea. Un reflejo de línea\(m\) a través de la línea discontinua se llevará\(m\) a sí mismo.
Estos hechos nos permiten llegar a una conclusión importante. Si dos líneas se cruzan en un punto, al que llamaremos\(O\), entonces una\(180^{\circ}\) rotación de las líneas con centro\(O\) muestra que los ángulos verticales son congruentes. Aquí hay un ejemplo:
Girar ambas líneas\(180^{\circ}\) alrededor\(O\) envía ángulo\(AOC\) a ángulo\(A'OC'\), siempre que tengan la misma medida. La rotación también envía ángulo\(AOC'\) a ángulo\(A'OC\).
Entradas en el glosario
Definición: Correspondiente
Cuando parte de una figura original coincide con parte de una copia, las llamamos partes correspondientes. Estos podrían ser puntos, segmentos, ángulos o distancias.
Por ejemplo, el punto\(B\) en el primer triángulo corresponde al punto\(E\) en el segundo triángulo. Segmento\(AC\) corresponde al segmento\(DF\).
Definición: Transformación rígida
Una transformación rígida es un movimiento que no cambia ninguna medida de una figura. Las traducciones, las rotaciones y las reflexiones son transformaciones rígidas, al igual que cualquier secuencia de éstas.
Definición: Ángulos verticales
Los ángulos verticales son ángulos opuestos que comparten el mismo vértice. Están formados por un par de líneas que se cruzan. Sus medidas de ángulo son iguales.
Por ejemplo, los ángulos\(AEC\) y\(DEB\) son ángulos verticales. Si el ángulo\(AEC\) mide\(120^{\circ}\), entonces el ángulo también\(DEB\) debe medir\(120^{\circ}\).
Ángulos\(AED\) y\(BEC\) son otro par de ángulos verticales.
Práctica
Ejercicio\(\PageIndex{4}\)
- Dibujar líneas paralelas\(AB\) y\(CD\).
- Escoge cualquier punto\(E\). Gire\(AB\) 90 grados en sentido horario alrededor\(E\).
- Gire la línea\(CD\) 90 grados en sentido horario alrededor\(E\).
- ¿Qué notas?
Ejercicio\(\PageIndex{5}\)
Usa el diagrama para encontrar las medidas de cada ángulo. Explica tu razonamiento.
- \(m\angle ABC\)
- \(m\angle EBD\)
- \(m\angle ABE\)
Ejercicio\(\PageIndex{6}\)
Puntos\(P\) y\(Q\) se trazan en una línea.
- Encuentra un punto\(R\) para que una rotación de 180 grados con centro\(R\) envíe\(P\) hacia\(Q\) y\(Q\) hacia\(P\).
- ¿Hay más de un punto\(R\) que funcione para la parte a?
Ejercicio\(\PageIndex{7}\)
En la imagen triángulo\(A'B'C'\) es una imagen de triángulo\(ABC\) después de una rotación. El centro de rotación es\(D\).
- ¿Cuál es la longitud del lado\(B'C'\)? Explica cómo sabes.
- ¿Cuál es la medida del ángulo\(B\)? Explica cómo sabes.
- ¿Cuál es la medida del ángulo\(C\)? Explica cómo sabes.
(De la Unidad 1.2.1)
Ejercicio\(\PageIndex{8}\)
El punto\((-4,1)\) se gira 180 grados en sentido antihorario usando el centro\((0,0)\). ¿Cuáles son las coordenadas de la imagen?
A:\((-1,-4)\)
B:\((-1,4)\)
C:\((4,1)\)
D:\((4,-1)\)
(De la Unidad 1.1.6)