1.2.2: Patrones de Rotación

Última actualización
Guardar como PDF

Page ID: 118672

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Rotemos figuras en un plano.

Ejercicio$\PageIndex{1}$: Building a Quadrilateral

Aquí hay un triángulo isósceles derecho.

Gire el triángulo$ABC$ 90 grados en sentido horario alrededor$B$.
Gire el triángulo$ABC$ 180 grados en sentido horario alrededor$B$.
Gire el triángulo$ABC$ 270 grados en sentido horario alrededor$B$.
¿Cómo se vería cuando giras los cuatro triángulos 90 grados en sentido horario alrededor$B$? ¿180 grados? ¿270 grados en sentido horario?

Ejercicio$\PageIndex{2}$: Rotating a Segment

Rotación de un segmento

Cree un segmento$AB$ y un punto$C$ que no esté en el segmento$AB$.

Gire el segmento$AB 180^{\circ}$ alrededor del punto$B$.
Gire el segmento$AB 180^{\circ}$ alrededor del punto$C$.

$clipboard_e297000b2b234fe3e8b15cd3c679a7989.png$

Construya el punto medio del segmento$AB$ con la herramienta Punto medio.

Gire el segmento$AB 180^{\circ}$ alrededor de su punto medio. ¿Cuál es la imagen de A?
Qué sucede cuando rotas un segmento$180^{\circ}$

¿Estás listo para más?

Aquí hay dos segmentos de línea. ¿Es posible rotar un segmento de línea al otro? Si es así, encuentra el centro de tal rotación. Si no, explica por qué no.

Ejercicio$\PageIndex{3}$: A Pattern of Four Triangles

Aquí hay un diagrama construido con tres transformaciones rígidas diferentes de triángulo$ABC$.

Usa el applet para responder a las preguntas. Puede ser útil restablecer la imagen después de cada pregunta.

Describir una transformación rígida que toma triángulo$ABC$ a triángulo$CDE$.
Describir una transformación rígida que toma triángulo$ABC$ a triángulo$EFG$.
Describir una transformación rígida que toma triángulo$ABC$ a triángulo$GHA$.
¿Los segmentos$AC$$CE$,$EG$, y$GA$ todos tienen la misma longitud? Explica tu razonamiento.

Resumen

Cuando aplicamos una rotación de 180 grados a un segmento de línea, hay varios resultados posibles:

El segmento se mapea a sí mismo (si el centro de rotación es el punto medio del segmento).
La imagen del segmento se solapa con el segmento y se encuentra en la misma línea (si el centro de rotación es un punto en el segmento).
La imagen del segmento no se superpone con el segmento (si el centro de rotación no está en el segmento).

También podemos construir patrones rotando una forma. Por ejemplo, el triángulo que$ABC$ se muestra aquí tiene$m(\angle A)=60$. Si giramos el triángulo$ABC$ 60 grados, 120 grados, 180 grados, 240 grados y 300 grados en el sentido de las agujas del reloj, podemos construir un hexágono.

Figura$\PageIndex{3}$: Se dibujan seis triángulos equiláteros idénticos de tal manera que cada triángulo se alinea con otro triángulo creado un hexágono. Uno de los triángulos está etiquetado como A B C y los 6 triángulos se encuentran en el punto común de A.

Entradas en el glosario

Definición: Correspondiente

Cuando parte de una figura original coincide con parte de una copia, las llamamos partes correspondientes. Estos podrían ser puntos, segmentos, ángulos o distancias.

Por ejemplo, el punto$B$ en el primer triángulo corresponde al punto$E$ en el segundo triángulo. Segmento$AC$ corresponde al segmento$DF$.

Definición: Transformación rígida

Una transformación rígida es un movimiento que no cambia ninguna medida de una figura. Las traducciones, las rotaciones y las reflexiones son transformaciones rígidas, al igual que cualquier secuencia de éstas.

Practica

Ejercicio$\PageIndex{4}$

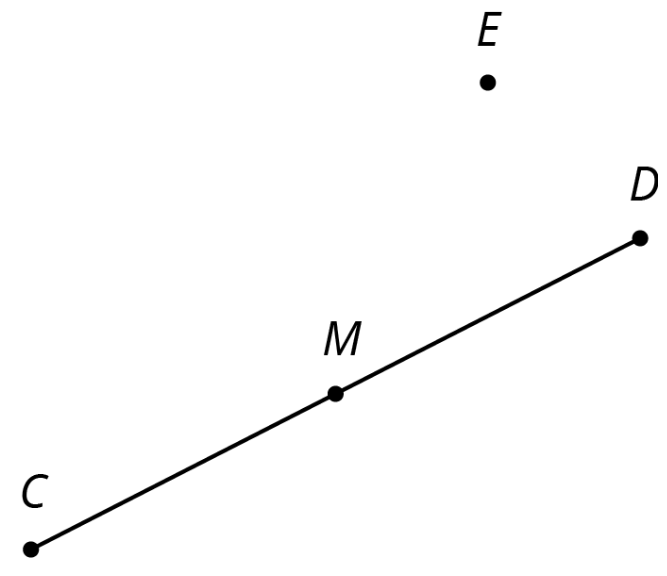
Para la figura aquí mostrada,

Gire el segmento$CD$$180^{\circ}$ alrededor del punto$D$.
Gire el segmento$CD$$180^{\circ}$ alrededor del punto$E$.
Gire el segmento$CD$$180^{\circ}$ alrededor del punto$M$.

Ejercicio$\PageIndex{5}$

Aquí hay un triángulo rectángulo isósceles:

Dibuja estas tres rotaciones de triángulo$ABC$ juntas.

Gire el triángulo$ABC$ 90 grados en sentido horario alrededor$A$.
Gire el triángulo$ABC$ 180 grados alrededor$A$.
Gire el triángulo$ABC$ 270 grados en sentido horario alrededor$A$.

Ejercicio$\PageIndex{6}$

Cada gráfica muestra dos polígonos$ABCD$ y$A'B'C'D'$. En cada caso, describir una secuencia de transformaciones que lleva$ABCD$ a$A'B'C'D'$.

Figura$\PageIndex{7}$: Cuadrilátero$ABCD$ y su imagen cuadrilátero$A'B'C'D'$ en un plano coordenado, origen$O$. Escala del eje horizontal negativo 5 a 5 por 1's. Escala del eje vertical negativo 2 a 3 por 1's. Las coordenadas de$ABCD$ son$A$ (negativo 3 coma 3),$B$ (negativo 4 coma 1),$C$ (negativo 2 coma negativo 1) y$D$ (negativo 2 coma 2). Las coordenadas de$A'B'C'D'$ son$A'$ (3 coma 2),$B'$ (4 coma 0),$C'$ (2 coma negativa 2) y$D'$ (2 coma 1).

Figura$\PageIndex{8}$: Cuadrilátero$ABCD$ y su imagen cuadrilátero$A'B'C'$ y$D'$ en plano coordenado, origen$O$. Escala del eje horizontal negativo 5 a 7 por 1's. Escala del eje vertical negativo 1 a 4 por 1's. Las coordenadas de$ABCD$ son$A$ (negativo 4 coma 1),$B$ (negativo 1 coma 0),$C$ (1 coma 3) y$D$ (negativo 2 coma 3). 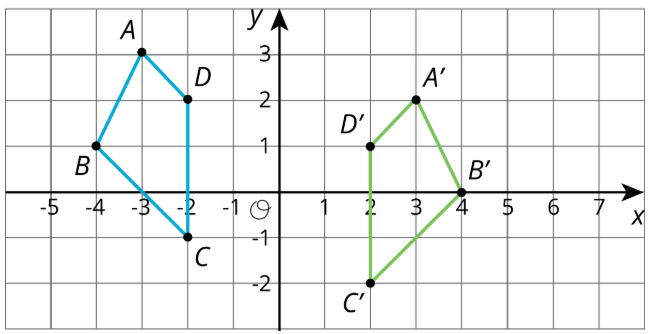Las coordenadas de$A'B'C'D'$ son$A'$ (4 coma 4),$B'$ (3 coma 1),$C'$ (6 coma negativa 1) y$D'$ (6 coma 2).

(De la Unidad 1.1.5)

Ejercicio$\PageIndex{7}$

Lin dice que puede mapear el Polígono A al Polígono B usando solo reflexiones. ¿Estás de acuerdo con Lin? Explica tu razonamiento.

Figura$\PageIndex{9}$: Dos cuadriláteros polígonos A y B en una cuadrícula. Dejar (0 coma 0) ser la esquina inferior izquierda. Entonces las coordenadas del polígono A son: (1 coma 4), (3 coma 7), (4 coma 5) y (3 coma 4). Las coordenadas del polígono B son: (5 coma 1), (7 coma 4), (5 coma 4) y (4 coma 3).

(De la Unidad 1.1.4)

Search

Text Color

Text Size

Margin Size

Font Type