Saltar al contenido principal
LibreTexts Español

2.1.2: Rejilla Circular

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118655

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Vamos a dilatar figuras en rejillas circulares.

    Ejercicio\(\PageIndex{1}\): Notice and Wonder: Concentric Circles

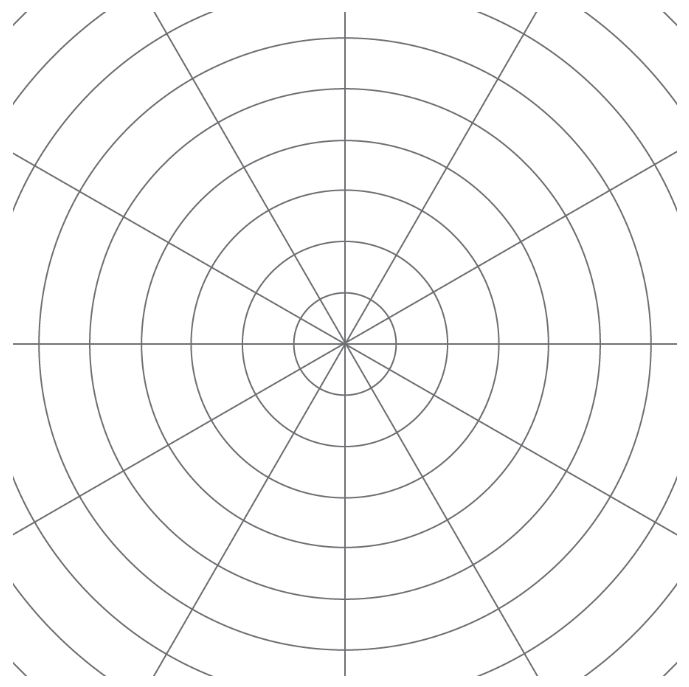
    clipboard_e1f994af6350e3fb3177e57a37421767f.png
    Figura\(\PageIndex{1}\)

    ¿Qué notas? ¿Qué te preguntas?

    Ejercicio\(\PageIndex{2}\): A Droplet on the Surface

    El círculo d más grande es una dilatación del círculo más pequeño c.\(P\) es el centro de dilatación.

    1. Dibuja cuatro puntos en el círculo más pequeño usando la herramienta Punto sobre objeto.
      clipboard_e7eed210813d6c4888f0f3899ef947223.png
    2. Dibuja los rayos a\(P\) través de cada uno de esos cuatro puntos. Seleccione la herramienta Rayos, luego punto\(P\) y luego el segundo punto.
      clipboard_ef7b116ea9fb641f6a2824f13434b9208.png
    3. Marque los puntos de intersección de los rayos y Círculo d seleccionando la herramienta Intersectar y haciendo clic en el punto de intersección.
      clipboard_e275af0c9be9b07c4f66cece47eca7e2b.png
    4. Completa la tabla. En la fila etiquetada S, escriba la distancia entre\(P\) y el punto en el círculo más pequeño en unidades de cuadrícula. En la fila etiquetada L, escriba la distancia entre\(P\) y el punto correspondiente en el círculo más grande en unidades de cuadrícula. Mida las distancias entre pares de puntos seleccionando la herramienta Distancia y luego haciendo clic en los dos puntos.
      clipboard_e4760109a4ecbf80413593c7e65231c46.png
    \(A\) \(B\) \(C\) \(D\)
    \(S\) \ (A\) "> \ (B\) "> \ (C\) "> \ (D\) ">
    \(L\) \ (A\) "> \ (B\) "> \ (C\) "> \ (D\) ">
    Mesa\(\PageIndex{1}\)

    5. El centro de dilatación es el punto\(P\). ¿Cuál es el factor de escala que lleva el círculo más pequeño al círculo más grande? Explica tu razonamiento.

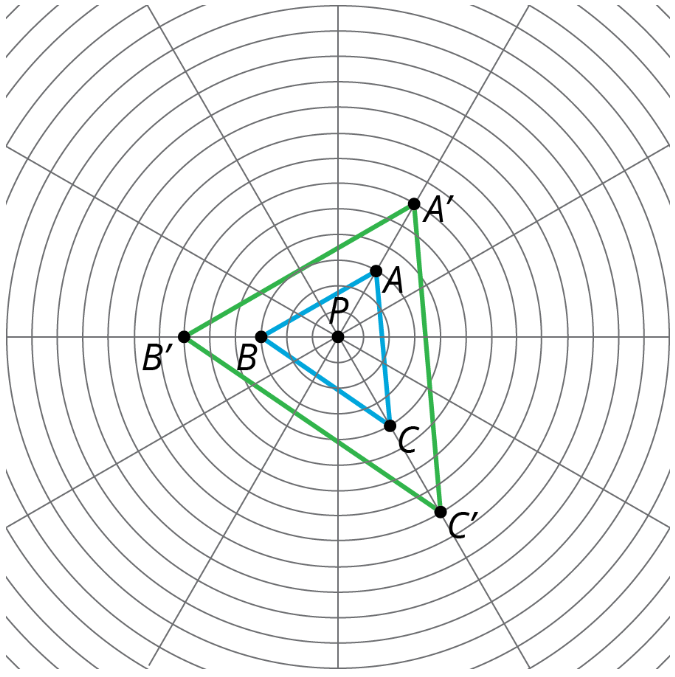
    Ejercicio\(\PageIndex{3}\): Quadrilateral on a Circular Grid

    Aquí hay un polígono\(ABCD\)

    1. Dilate cada vértebra del polígono\(ABCD\) utilizando\(P\) como centro de dilatación y un factor de escala de\(2\).
    2. Dibuja segmentos entre los puntos dilatados para crear un nuevo polígono.
    3. ¿Cuáles son algunas cosas que notas sobre el nuevo polígono?
    4. Elige algunos puntos más a los lados del polígono original y transfórmalos usando la misma dilatación. ¿Qué notas?
    5. Dilate cada vértice del polígono\(ABCD\) utilizando\(P\) como centro de dilatación y un factor de escala de\(\frac{1}{2}\).
    6. ¿Qué notas sobre este nuevo polígono?

    ¿Estás listo para más?

    Supongamos que\(P\) es un punto no en el segmento de línea\(\overline{WX}\). Dejar\(\overline{YZ}\) ser la dilatación del segmento lineal\(\overline{WX}\) utilizando\(P\) como centro con factor de escala 2. Experimente usando una cuadrícula circular para hacer predicciones sobre si cada una de las siguientes afirmaciones debe ser verdadera, podría ser verdadera o debe ser falsa.

    1. \(\overline{YZ}\)es el doble de largo\(\overline{WX}\)
    2. \(\overline{YZ}\)es cinco unidades más largas que\(\overline{WX}\)
    3. El punto\(P\) está encendido\(\overline{YZ}\)
    4. \(\overline{YZ}\)y\(\overline{WX}\) se cruzan.

    Ejercicio\(\PageIndex{4}\): A Quadrilateral and Concentric Circles

    1. Dilar polígono\(EFGH\) usando\(Q\) como centro de dilatación y un factor de escala de\(\frac{1}{3}\). La imagen de ya\(F\) se muestra en el diagrama. (Es posible que necesite dibujar más rayos para encontrar las imágenes de otros puntos).\(Q\)

    Resumen

    Una rejilla circular como esta puede ser útil para realizar dilataciones.

    El radio del círculo más pequeño es una unidad, y el radio de cada círculo sucesivo es una unidad más que el anterior.

    clipboard_e5d49cb2c967ab76568525fb594ddc556.png
    Figura\(\PageIndex{2}\)

    Para realizar una dilatación, necesitamos un centro de dilatación, un factor de escala y un punto para dilatar. En la imagen,\(P\) está el centro de dilatación. Con un factor de escala de 2, cada punto permanece en el mismo rayo desde\(P\), pero su distancia de\(P\) dobles:

    clipboard_e2f2319de4c59af0cc10589076c066930.png
    Figura\(\PageIndex{3}\)

    Dado que los círculos en la cuadrícula están separados a la misma distancia, el segmento\(PA'\) tiene el doble de longitud del segmento\(PA\), y lo mismo se mantiene para los otros puntos.

    Entradas en el glosario

    Definición: Centro de una Dilatación

    El centro de una dilatación es un punto fijo en un plano. Es el punto de partida desde el que medimos distancias en una dilatación.

    En este diagrama, el punto\(P\) es el centro de la dilatación.

    clipboard_e2f3b2b4783c0d5233cdcfab1e1a44ca6.png
    Figura\(\PageIndex{4}\)

    Definición: Dilatación

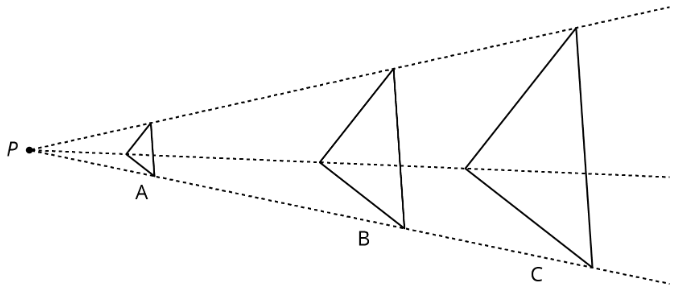
    Una dilatación es una transformación en la que cada punto de una figura se mueve a lo largo de una línea y cambia su distancia desde un punto fijo. El punto fijo es el centro de la dilatación. Todas las distancias originales se multiplican por el mismo factor de escala.

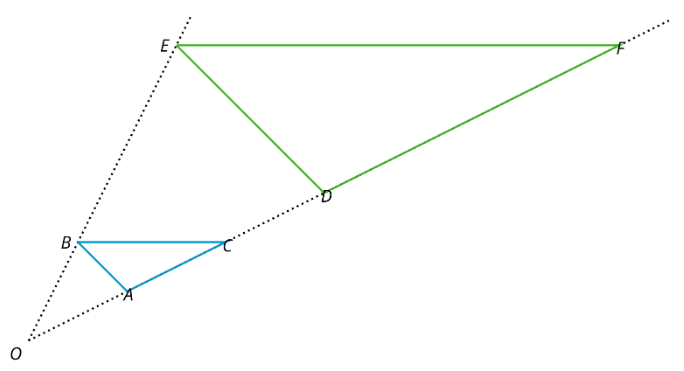
    Por ejemplo, triángulo\(DEF\) es una dilatación de triángulo\(ABC\). El centro de dilatación es\(O\) y el factor de escala es 3.

    Esto significa que cada punto del triángulo\(DEF\) está 3 veces más lejos\(O\) de cada punto correspondiente del triángulo\(ABC\).

    clipboard_edaebac256db4e50e29e5ccd173f94779.png
    Figura\(\PageIndex{5}\)

    Definición: Factor de Escala

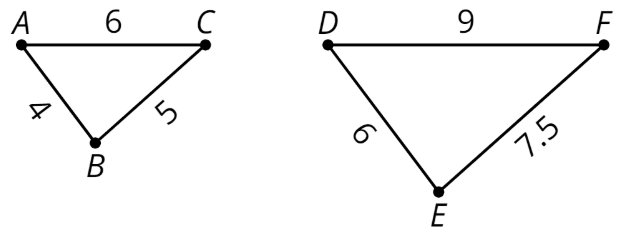
    Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. Este número se llama factor de escala.

    En este ejemplo, el factor de escala es 1.5, porque\(4\cdot (1.5)=6\),\(5\cdot (1.5)=7.5\), y\(6\cdot (1.5)=9\).

    clipboard_efd0588f0a74adfcd3856c842a8bb0c2b.png
    Figura\(\PageIndex{6}\)

    Practica

    Ejercicio\(\PageIndex{5}\)

    Aquí están Círculos\(c\) y\(d\). Punto\(O\) es el centro de dilatación, y la dilatación lleva Círculo\(c\) a Círculo\(d\).

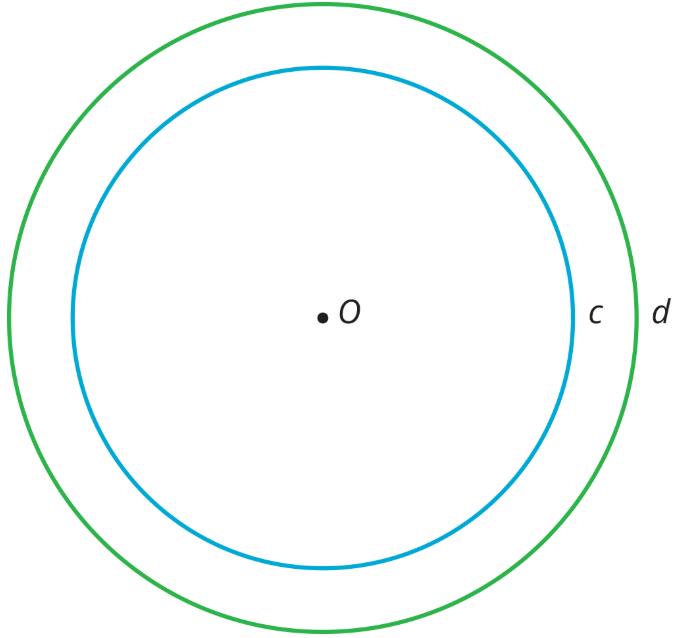
    clipboard_e6c0279b6bd7a35a4e0a01348040b1882.png
    Figura\(\PageIndex{7}\)
    1. Trazar un punto en Círculo\(c\). Etiquete el punto\(P\). Trazar donde\(P\) va cuando se aplica la dilatación.
    2. Trazar un punto en Círculo\(d\). Etiquete el punto\(Q\). Trazar un punto al que lleva la dilatación\(Q\).

    Ejercicio\(\PageIndex{6}\)

    Aquí hay un triángulo\(ABC\).

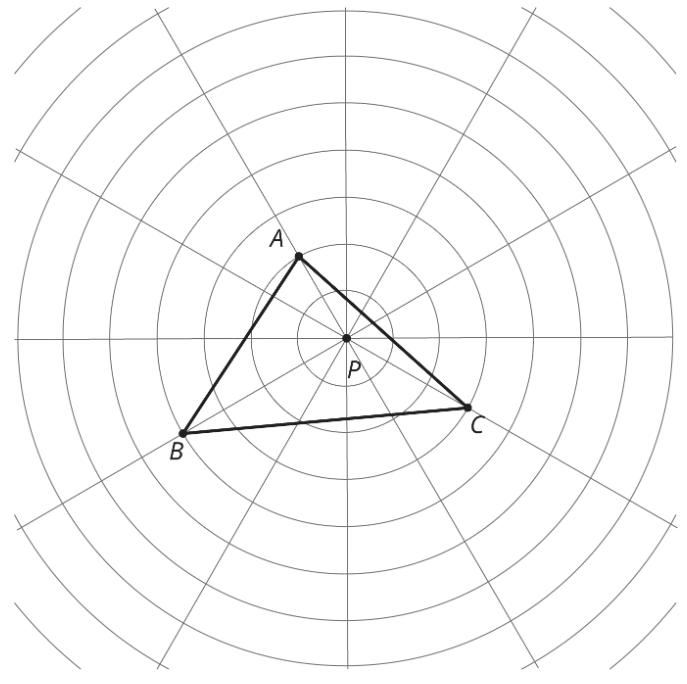
    clipboard_e01e18e244b1d93a50eaebeccbec331cc.png
    Figura\(\PageIndex{8}\)
    1. Dilate cada vértice del triángulo\(ABC\) usando\(P\) como centro de dilatación y un factor de escala de 2. Dibuja el triángulo que conecta los tres nuevos puntos.
    2. Dilate cada vértice del triángulo\(ABC\) usando\(P\) como centro de dilatación y un factor de escala de\(\frac{1}{2}\). Dibuja el triángulo que conecta los tres nuevos puntos.
    3. Mida el lado más largo de cada uno de los tres triángulos. ¿Qué notas?
    4. Mida los ángulos de cada triángulo. ¿Qué notas?

    Ejercicio\(\PageIndex{7}\)

    Describe una transformación rígida que podrías usar para mostrar que los polígonos son congruentes.

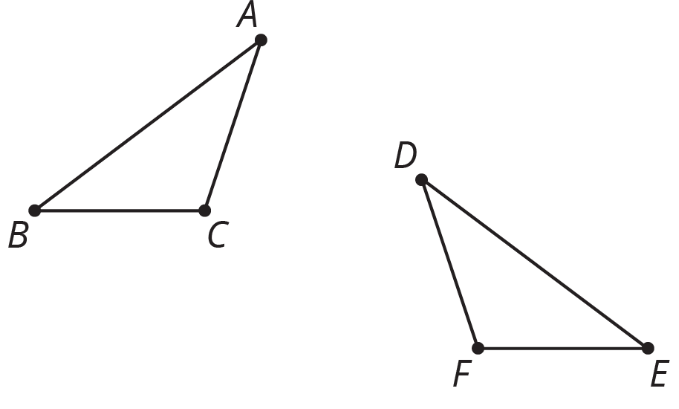
    clipboard_ee7e98eaf361d067a5ef51bec1474b9a9.png
    Figura\(\PageIndex{9}\)

    (De la Unidad 1.3.2)

    Ejercicio\(\PageIndex{8}\)

    La línea ha sido particionada en tres ángulos.

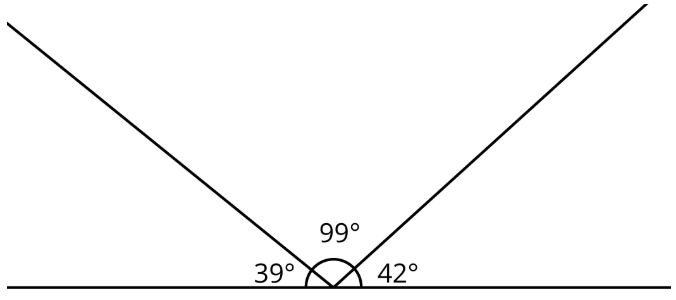
    clipboard_e1b8a20c83455d034c503b7725bff8155.png
    Figura\(\PageIndex{10}\): Una línea recta con dos rayos que salen de un solo punto. Uno inclinado hacia arriba y hacia la izquierda. Uno inclinado hacia arriba y hacia la derecha. Se forman tres ángulos. 39 grados. 99 grados. 42 grados.

    ¿Hay un triángulo con estas tres medidas angulares? Explique.

    (De la Unidad 1.4.2)

    This page titled 2.1.2: Rejilla Circular is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.