3.2.3: Representaciones de Relaciones Lineales

Lección

Escribamos ecuaciones a partir de soluciones reales.

Ejercicio\(\PageIndex{1}\): Estimation: Which Holds More?

¿Qué vaso contendrá más agua? ¿El menos?

Figura\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\): Rising Water Levels

Mueve el círculo verde para establecer el nivel inicial de agua a un valor que tú o tu profesor elijan.

1. Cuál es el volumen,\(V\), en el cilindro después de agregar:
   1. ¿3 objetos?
   2. ¿7 objetos?
   3. \(x\)objetos? Explica tu razonamiento.
2. Si quisieras que el agua alcanzara la marca más alta en el cilindro, ¿cuántos objetos necesitarías?
3. Trazar y etiquetar puntos que muestren sus medidas del experimento.
4. Traza y etiqueta un punto que muestre la profundidad del agua antes de agregar cualquier objeto.
5. Los puntos deben caer en una línea. Usa la herramienta Línea para dibujar esta línea.
6. Calcular la pendiente de la línea usando varios triángulos diferentes. ¿Importa qué triángulo uses para calcular la pendiente? ¿Por qué o por qué no?
7. La ecuación de la línea en el experimento tiene dos números y dos variables. ¿Qué cantidades físicas representan los dos números? ¿Qué\(V\) representa y qué\(x\) representa?

¿Estás listo para más?

Una situación es representada por la ecuación\(y=5+\frac{1}{2}x\).

1. Inventar una historia para esta situación.
2. Grafica la ecuación.
3. ¿Qué representan los\(\frac{1}{2}\) y los 5 en su situación?
4. ¿Dónde ves el\(\frac{1}{2}\) y 5 en la gráfica?

Ejercicio\(\PageIndex{3}\): Calculate the Slope

Figura\(\PageIndex{2}\): 3 gráficas de líneas etiquetadas A, B, C. gráfica A, triángulo rectángulo dibujado hacia la derecha y hacia arriba desde el punto 1 coma 3 hasta el punto 4 coma 9, ambos en la línea. gráfico B, triángulo rectángulo dibujado hacia la derecha y hacia arriba desde el punto 2 coma 1 y 5 décimas hasta el punto 10 coma 3 y 5 décimas, ambos en la línea. gráfico C, triángulo rectángulo dibujado a la derecha y hacia arriba desde el punto 10 coma 35 hasta el punto 30 coma 75, ambos en la línea.

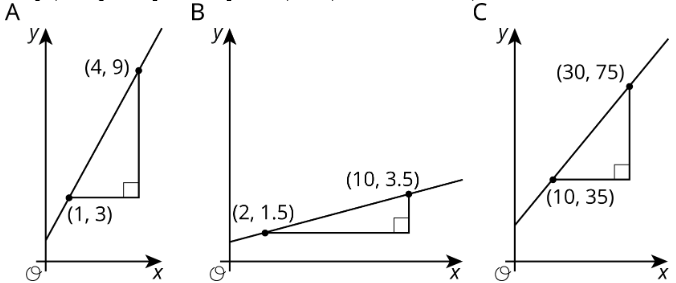
1. Para cada registro gráfico:

   Mesa\(\PageIndex{1}\)

   cambio vertical	cambio horizontal	pendiente

2. Describir un procedimiento para encontrar la pendiente entre dos puntos cualesquiera de una línea.
3. Escriba una expresión para la pendiente de la línea en la gráfica usando las letras\(u\),\(v\),\(s\), y\(t\).

Figura\(\PageIndex{3}\)

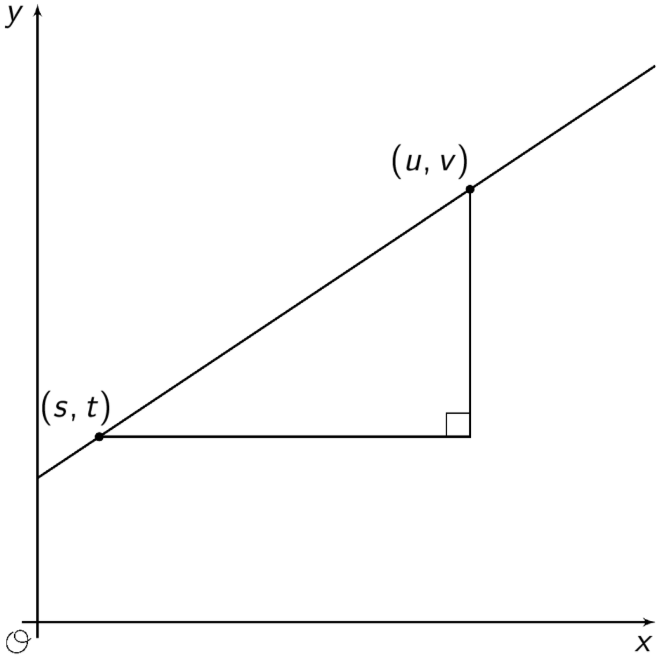
Resumen

Digamos que tenemos un cilindro de vidrio lleno de 50 ml de agua y un manojo de canicas que son de 3 ml de volumen. Si dejamos caer canicas en el cilindro una a la vez, podemos observar que la altura del agua aumenta en la misma cantidad, 3 ml, por cada una agregada. Esta tasa constante de cambio significa que existe una relación lineal entre el número de canicas y la altura del agua. Agrega una canica, la altura del agua sube 3 ml. Agrega 2 canicas, la altura del agua sube 6 ml. Agrega\(x\) canicas, la altura del agua sube\(3x\) ml.

Razonando de esta manera, podemos calcular que la altura\(y\),, del agua para\(x\) canicas es\(y=3x+50\). Cualquier relación lineal se puede expresar en la forma\(y=mx+b\) usando solo la tasa de cambio,\(m\), y la cantidad inicial,\(b\). El 3 representa la tasa de cambio, o pendiente de la gráfica, y el 50 representa la cantidad inicial, o intercepción vertical de la gráfica. Aprenderemos algunas formas más de pensar sobre esta ecuación en lecciones futuras.

Ahora, ¿y si no tuviéramos una descripción que usar para averiguar la pendiente y la intercepción vertical? ¡Eso está bien siempre y cuando podamos encontrar algunos puntos en la línea! Para la línea graficada aquí, dos de los puntos en la línea son\((3,3)\) y\((9,5)\) y podemos usar estos puntos para dibujar en un triángulo de pendiente como se muestra:

Figura\(\PageIndex{4}\)

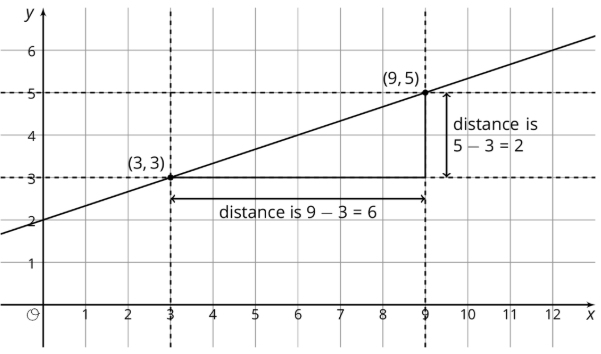
La pendiente de esta línea es el cociente de la longitud del lado vertical del triángulo de pendiente y la longitud del lado horizontal del triángulo de pendiente. Entonces la pendiente,\(m\), es\(\frac{vertical change}{horizontal change}=\frac{2}{6}=\frac{1}{3}\). También podemos ver en la gráfica que la intercepción vertical,\(b\), es 2. Armando estos, podemos decir que la ecuación para esta línea es\(y=\frac{1}{3}x+2\).

Entradas en el glosario

Definición: Relación lineal

Una relación lineal entre dos cantidades significa que están relacionadas así: Cuando una cantidad cambia en una cantidad determinada, la otra cantidad siempre cambia por una cantidad establecida. En una relación lineal, una cantidad tiene una tasa de cambio constante con respecto a la otra.

La relación se llama lineal porque su gráfica es una línea.

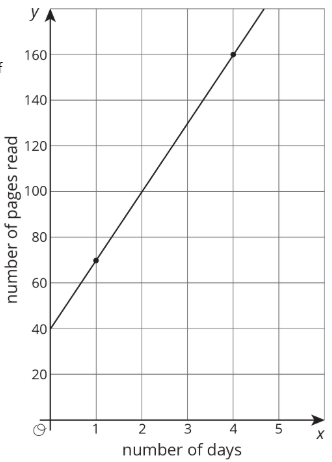
La gráfica muestra una relación entre el número de días y el número de páginas leídas.

Cuando el número de días aumenta en 2, el número de páginas leídas siempre aumenta en 60. La tasa de cambio es constante, 30 páginas por día, por lo que la relación es lineal.

Figura\(\PageIndex{5}\)

Definición: Intercepción vertical

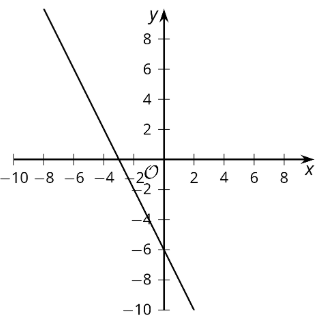
La intercepción vertical es el punto donde la gráfica de una línea cruza el eje vertical.

La intercepción vertical de esta línea es\((0,-6)\) o apenas -6.

Figura\(\PageIndex{6}\)

Practica

Ejercicio\(\PageIndex{4}\)

Cree una gráfica que muestre tres relaciones lineales con diferentes -intercepciones utilizando las siguientes pendientes, y escriba una ecuación para cada línea.

Pistas:

• \(\frac{1}{5}\)
• \(\frac{3}{5}\)
• \(\frac{6}{5}\)

Figura\(\PageIndex{7}\)

Ejercicio\(\PageIndex{5}\)

La gráfica muestra la altura en pulgadas,\(h\), de una planta de bambú\(t\) meses después de haber sido plantada.

Figura\(\PageIndex{8}\)

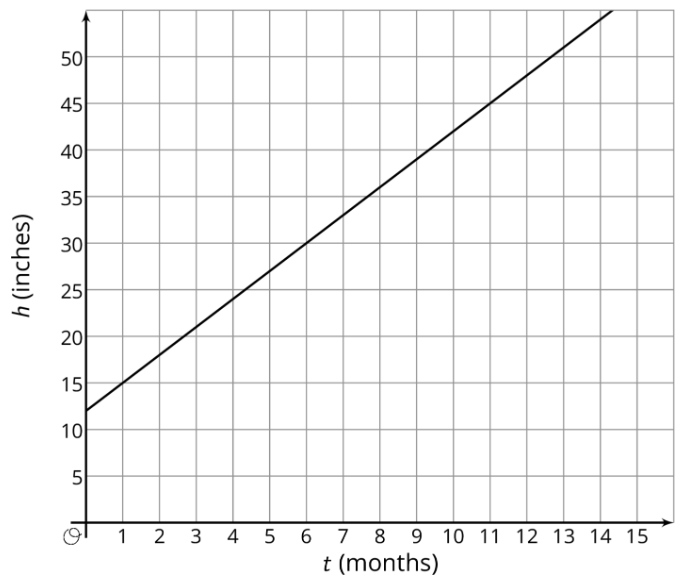
1. Escribir una ecuación que describa la relación entre\(h\) y\(t\).
2. ¿Después de cuántos meses tendrá la planta de bambú 66 pulgadas de alto? Explica o muestra tu razonamiento.

Ejercicio\(\PageIndex{6}\)

Aquí hay recetas para dos pasteles de plátano diferentes. La información de la primera receta se muestra en la tabla.

Mesa\(\PageIndex{2}\)

azúcar (tazas)	harina (tazas)
\(\frac{1}{2}\)	\(\frac{3}{4}\)
\(2\frac{1}{2}\)	\(3\frac{3}{4}\)
\(3\)	\(4\frac{1}{2}\)

La relación entre tazas de harina\(y\) y tazas de azúcar\(x\) en la segunda receta es\(y=\frac{7}{4}x\).

1. Si usaste 4 tazas de azúcar, ¿cuánta harina necesita cada receta?
2. ¿Cuál es la constante de proporcionalidad para cada situación y qué significa?

(De la Unidad 3.1.4)

Ejercicio\(\PageIndex{7}\)

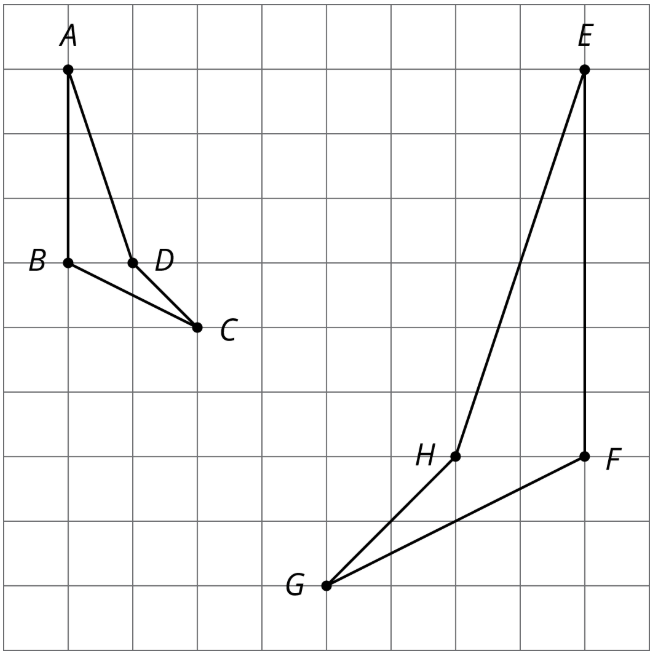
Demostrar que las dos figuras son similares al identificar una secuencia de traslaciones, rotaciones, reflexiones y dilataciones que lleva la figura más grande a la más pequeña.

Figura ABCD y figura EFGH sobre una cuadrícula de 10 por 10. dejando esquina inferior izquierda = 0 coma 0, A = 1 coma 9, B = 1 coma 6, C = 3 coma 5, D = 2 coma 6, E = 9 coma 9, F = 9 coma 3, G = 5 coma 1, H = 7 coma 3.

(De la Unidad 2.2.1)