4.3.3: Sistemas de Ecuaciones

Lección

Aprendamos qué es un sistema de ecuaciones.

Ejercicio\(\PageIndex{1}\): Milkshakes

Diego y Lin están tomando batidos. Lin empieza con 12 onzas y bebe\(\frac{1}{4}\) una onza por segundo. Diego comienza con 20 onzas y bebe\(\frac{2}{3}\) una onza por segundo.

1. ¿Cuánto tardarán Lin y Diego en terminar sus batidos?
2. Sin graficar, explique cómo serían las gráficas en esta situación. Piense en la pendiente, las intercepciones, las etiquetas de eje, las unidades y los puntos de intersección para guiar su pensamiento.
3. Discuta su descripción con su pareja. Si no estás de acuerdo, trabaja para llegar a un acuerdo.

Ejercicio\(\PageIndex{2}\): Passing on the Trail

Hay una ruta de senderismo cerca del pueblo donde viven Han y Jada que comienza en un estacionamiento y termina en un lago. Han y Jada deciden caminar desde el estacionamiento hasta el lago y regresar, pero inician sus caminatas en diferentes momentos.

En el momento en que Han llega al lago y comienza a dar la vuelta, Jada se encuentra a 0.6 millas del estacionamiento y camina a una velocidad constante de 3.2 millas por hora hacia el lago. La distancia de Han\(d\),, desde el estacionamiento se puede expresar como\(d=-2.4t+4.8\), donde\(t\) representa el tiempo en horas desde que salió del lago.

1. ¿Cuál es una ecuación para la distancia de Jada del estacionamiento mientras se dirige hacia el lago?
2. Dibuja ambas gráficas: una que representa la ecuación de Han y otra que representa la ecuación de Jada. Es importante ser muy precisos.
3. Fnd el punto donde las dos gráficas se cruzan entre sí. ¿Cuáles son las coordenadas de este punto?
4. ¿Qué significan las coordenadas en esta situación?
5. ¿Qué tiene que ser cierto sobre la relación entre estas coordenadas y la ecuación de Jada?
6. ¿Qué tiene que ser cierto sobre la relación entre estas coordenadas y la ecuación de Han?

Ejercicio\(\PageIndex{3}\): Stacks of Cups

Una pila de tazas\(n\) pequeñas tiene una altura,\(h\), en centímetros de\(h=1.5n+6\). Una pila de tazas\(n\) grandes tiene una altura,\(h\), en centímetros de\(h=1.5n+9\).

1. Grafica las ecuaciones para cada copa en el mismo conjunto de ejes. Asegúrese de etiquetar los ejes y decidir sobre una escala apropiada.
2. ¿Para qué número de policías tendrán la misma altura las dos pilas?

Resumen

Un sistema de ecuaciones es un conjunto de 2 (o más) ecuaciones donde las variables representan los mismos valores desconocidos. Por ejemplo, supongamos que se plantan dos tipos diferentes de bambú al mismo tiempo. La planta A comienza a 6 pies de altura y crece a un ritmo constante de\(\frac{1}{4}\) pie cada día. La planta B comienza a 3 pies de altura y crece a un ritmo constante de\(\frac{1}{2}\) pie cada día. Podemos escribir ecuaciones\(y=\frac{1}{4}x+6\) para la Planta A y\(y=\frac{1}{2}x+3\) para la Planta B, donde\(x\) representa el número de días después de ser plantada, y representa la altura. Podemos escribir este sistema de ecuaciones.

\[\left\{\begin{array}{c} {y=\frac{1}{4}x+6}\\{y=\frac{1}{2}x+3}\end{array}\right.\nonumber\]

Resolver un sistema de ecuaciones significa encontrar los valores de\(x\) y\(y\) que hacen que ambas ecuaciones sean verdaderas al mismo tiempo. Una forma que hemos visto para encontrar la solución a un sistema de ecuaciones es graficar ambas líneas y encontrar el punto de intersección. El punto de intersección representa el par de\(x\) y\(y\) los valores que hacen que ambas ecuaciones sean verdaderas. Aquí hay una gráfica para el ejemplo de bambú:

Figura\(\PageIndex{1}\): Gráfica de dos líneas, origen O, con cuadrícula. Eje horizontal, tiempo en días, escala 0 a 13, por 1's. Eje vertical, altura en pies, escala 0 a 12, por 1's. Una línea, etiquetada Planta A, cruza el eje y en 6. Una línea, etiquetada Planta B, cruza el eje y en 3. Las líneas se cruzan en el punto 12 coma 9.

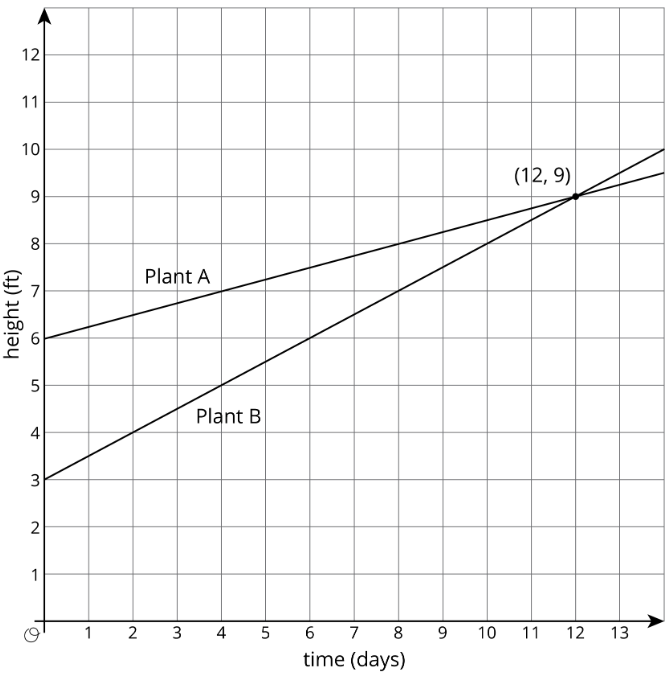
La solución a este sistema de ecuaciones es\((12,9)\), lo que significa que ambas plantas de bambú tendrán 9 pies de altura después de 12 días.

Hemos visto sistemas de ecuaciones que no tienen soluciones, una solución e infinitamente muchas soluciones.

• Cuando las líneas no se cruzan, no hay solución. (Las líneas que no se cruzan son paralelas.)
• Cuando las líneas se cruzan una vez, hay una solución.
• Cuando las líneas están justo una encima de la otra, hay infinitamente muchas soluciones.

En lecciones futuras, veremos que algunos sistemas no se pueden resolver fácilmente mediante gráficos, sino que se pueden resolver fácilmente usando álgebra.

Entradas en el glosario

Definición: Sistema de ecuaciones

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones. Cada ecuación contiene dos o más variables. Queremos encontrar valores para las variables que hagan verdaderas todas las ecuaciones.

Estas ecuaciones conforman un sistema de ecuaciones:

\[\left\{\begin{array}{c}{x+y=-2}\\{x-y=12}\end{array}\right.\nonumber\]

La solución a este sistema es\(x=5\) y\(y=-7\) porque cuando estos valores son sustituidos por\(x\) y\(y\), cada ecuación es verdadera:\(5+(-7)=-2\) y\(5-(-7)=12\).

Practica

Ejercicio\(\PageIndex{4}\)

Aquí está la gráfica para una ecuación en un sistema de ecuaciones:

Figura\(\PageIndex{2}\): Gráfica de una línea en el plano x y, origen O, con cuadrícula. Eje horizontal, escala negativa 6 a 6, por 1's. Eje vertical, escala negativa 6 a 6, por 1's. La línea cruza el eje y en 4. Pasa por el punto 4 coma 1.

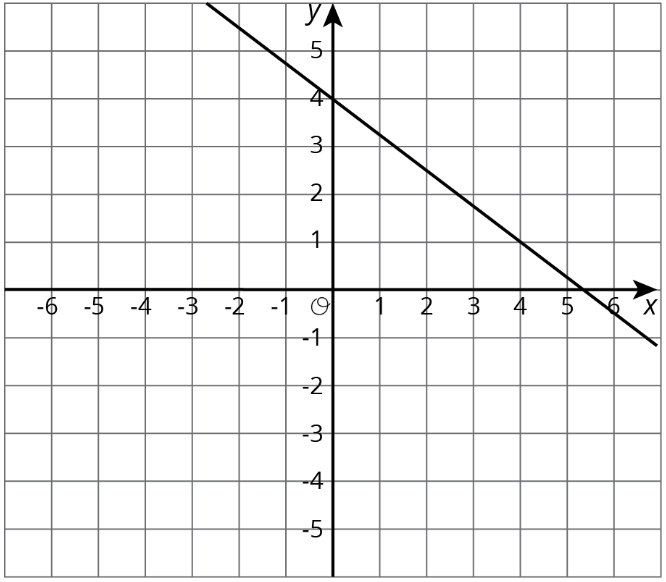
1. Escribe una segunda ecuación para el sistema para que tenga infinitamente muchas soluciones.
2. Escribe una segunda ecuación cuya gráfica pase por\((0,1)\) lo que el sistema no tenga soluciones.
3. Escribir una segunda ecuación cuya gráfica pasa por\((0,2)\) lo que el sistema tiene una solución en\((4,1)\).

Ejercicio\(\PageIndex{5}\)

Crear una segunda ecuación para que el sistema no tenga soluciones.

\[\left\{\begin{array}{c}{y=\frac{3}{4}x-4}\\{}\end{array}\right.\nonumber\]

Ejercicio\(\PageIndex{6}\)

Andre es el encargado de cocinar brócoli y calabacín para un grupo numeroso. Tiene que gastar todos los 17 dólares que tiene y puede llevar 10 libras de verduras. El calabacín cuesta $1.50 por libra y el brócoli cuesta $2 por libra. Una gráfica muestra combinaciones de calabacín y brócoli que pesan 10 libras y la otra muestra combinaciones de calabacín y brócoli que cuestan 17 dólares.

Figura\(\PageIndex{3}\): La gráfica de dos líneas que se cruzan en el plano x y. La primera línea se inclinó hacia abajo y hacia la derecha y pasa por el punto 4 coma 5 punto 5. La segunda línea se inclinó hacia abajo y hacia la derecha y pasa por el punto 5 coma 5. Las líneas se cruzan en el punto 6 coma 4.

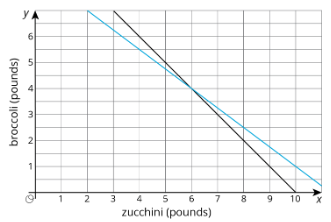
1. Nombra una combinación de verduras que pese 10 libras pero que no cueste $17.
2. Nombra una combinación de verduras que cueste $17 pero que no pese 10 libras.
3. ¿Cuántas libras cada uno de calabacín y brócoli puede obtener Andre para que gaste todos los 17 dólares y obtenga 10 libras de verduras?

(De la Unidad 4.3.2)

Ejercicio\(\PageIndex{7}\)

La temperatura en grados Fahrenheit,\(F\), está relacionada con la temperatura en grados Celsius,\(C\), por la ecuación\(F=\frac{9}{5}C+32\)

1. En el desierto del Sahara, las temperaturas suelen alcanzar los 50 grados centígrados. ¿Cuántos grados Fahrenheit es este?
2. En partes de Alaska, las temperaturas pueden alcanzar -60 grados Fahrenheit. ¿Cuántos grados centígrados es este?
3. Hay una temperatura donde los grados Fahrenheit y grados Celsius son los mismos, así que eso\(C=F\). Utilice la expresión de la ecuación, donde\(F\) se expresa en términos de\(C\), para resolver para esta temperatura.

(De la Unidad 4.3.1)