Saltar al contenido principal
LibreTexts Español

4.3.4: Resolver Sistemas de Ecuaciones

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118694

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Lección

    Resolvamos sistemas de ecuaciones.

    Ejercicio\(\PageIndex{1}\): True or False: Two Lines

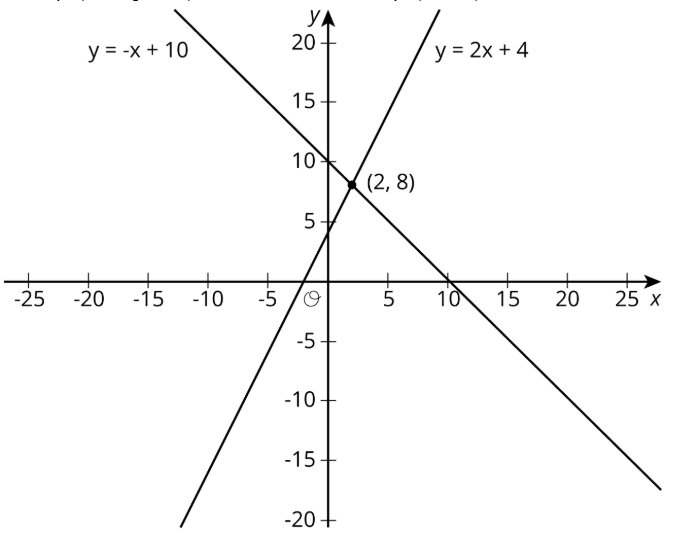
    clipboard_e95deaeeae86c267975aefa550fdd46a9.png
    Figura\(\PageIndex{1}\): Gráfica de 2 líneas, origen O. Eje horizontal, escala negativa 25 a 25, por 5's. Eje vertical, escala negativa 20 a 20, por 5's. Una línea es etiquetada y es igual a negativo x más 10. Otra línea está etiquetada y es igual a 2 x más 4. Las líneas se cruzan en el punto 2 coma 8.

    Usa las líneas para decidir si cada declaración es verdadera o falsa. Esté preparado para explicar su razonamiento usando las líneas.

    1. Una solución a\(8=-x+10\) es 2.
    2. Una solución a\(2=2x+4\) es 8.
    3. Una solución a\(-x+10=2x+4\) es 8.
    4. Una solución a\(-x+10=2x+4\) es 2.
    5. No hay valores de\(x\) y\(y\) que hacen\(y=-x+10\) y\(y=2x+4\) verdad al mismo tiempo.

    Ejercicio\(\PageIndex{2}\): Matching Graphs to Systems

    Aquí hay tres sistemas de ecuaciones gráficas en un plano de coordenadas:

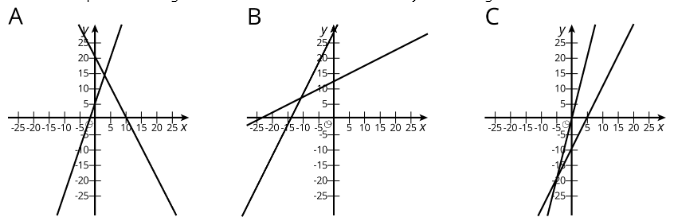
    clipboard_e69809836db8a306cc07f2878837c8879.png
    Figura\(\PageIndex{2}\): Tres gráficas, con dos líneas cada una, en el plano x y, origen O. Todas las gráficas tienen una escala de 25 a 25 negativas tanto en el eje x como en el eje y. Gráfica A. Una línea se inclinó hacia abajo y hacia la derecha. Cruza el eje x en 10 y el eje y en 20. Otra línea se inclinó hacia arriba y hacia la derecha. Cruza el eje y en 5. Cruza el eje x a la izquierda del origen. Gráfica B. Una línea se inclinó hacia arriba y hacia la derecha. Cruza el eje y entre 25 y 30. Cruza el eje x entre negativo 10 y negativo 15. Otra línea se inclinó hacia arriba y hacia la derecha. Cruza el eje y entre 10 y 15. Cruza el eje x entre negativo 20 y negativo 25. Gráfica C. Una línea se inclinó hacia arriba y hacia la derecha. Cruza el eje x entre 0 y 5. Cruza el eje y entre 0 y negativo 5. Otra línea se inclinó hacia arriba y hacia la derecha. Cruza el eje x en 5 y el eje y en negativo 10.
    1. Haga coincidir cada figura con uno de los sistemas de ecuaciones que se muestran aquí.
      1. \(\left\{\begin{array}{l}{y=3x+5}\\{y=-2x+20}\end{array}\right.\)
      2. \(\left\{\begin{array}{l}{y=2x-10}\\{y=4x-1}\end{array}\right.\)
      3. \(\left\{\begin{array}{l}{y=0.5x+12}\\{y=2x+27}\end{array}\right.\)
    2. Encuentre la solución para cada sistema y luego verifique que su solución sea razonable en la gráfica.
    • Observe que los deslizadores establecen los valores del coeficiente y el término constante en cada ecuación.
    • Cambiar los deslizadores a los valores del coeficiente y el término constante en el siguiente par de ecuaciones.
    • Haga clic en el lugar donde se cruzan las líneas y debería aparecer un punto etiquetado.

    Ejercicio\(\PageIndex{3}\): Different Types of Systems

    Tu profesor te dará una página con 6 sistemas de ecuaciones.

    1. Grafica cada sistema de ecuaciones escribiendo cada par de ecuaciones en el applet, una a la vez.
    2. Describir cómo se ve la gráfica de un sistema de ecuaciones cuando tiene.
      1. 1 solución
      2. 0 soluciones
      3. infinitamente muchas soluciones

    Usa el applet para confirmar tu respuesta a la pregunta 2.

    ¿Estás listo para más?

    Las gráficas de las ecuaciones\(Ax+By=15\) y se\(Ax-By=9\) cruzan en\((2,1)\). Encontrar\(A\) y\(B\). Muestra o explica tu razonamiento.

    Resumen

    A veces es más fácil resolver un sistema de ecuaciones sin tener que graficar las ecuaciones y buscar un punto de intersección. En general, siempre que estemos resolviendo un sistema de ecuaciones escritas como

    \[\left\{\begin{array}{l}{y=\text{[some stuff]}}\\{y=\text{[some other stuff]}}\end{array}\right.\nonumber\]

    sabemos que estamos buscando un par de valores\((x,y)\) que hagan verdaderas ambas ecuaciones. En particular, sabemos que el valor para\(y\) será el mismo en ambas ecuaciones. Eso significa que

    \[\text{[some stuff]}=\text{[some other stuff]}\nonumber\]

    Por ejemplo, mira este sistema de ecuaciones:

    \[\left\{\begin{array}{l}{y=2x+6}\\{y=-3x-4}\end{array}\right.\nonumber\]

    Dado que el\(y\) valor de la solución es el mismo en ambas ecuaciones, entonces sabemos\(2x+6=-3x-4\)

    Podemos resolver esta ecuación para\(x\):

    \[\begin{aligned} 2x+6&=-3x-4 \\ 5x+6&=-4 &\text{add 3x to each side} \\ 5x&=-10 &\text{subtract 6 from each side} \\ x&=-2 &\text{divide each side by 5}\end{aligned}\nonumber\]

    Pero esto es sólo la mitad de lo que estamos buscando: conocemos el valor para\(x\), pero necesitamos el valor correspondiente para\(y\). Dado que ambas ecuaciones tienen el mismo\(y\) valor, podemos usar cualquiera de las dos ecuaciones para encontrar el\(y\) -value:

    \(y=2(-2)+6\)

    O

    \(y=-3(-2)-4\)

    En ambos casos, nos encontramos con eso\(y=2\). Entonces la solución al sistema es\((-2,2)\). Podemos verificar esto graficando ambas ecuaciones en el plano de coordenadas.

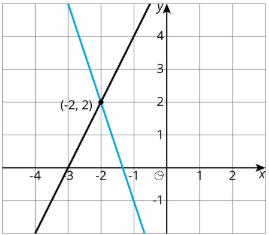
    clipboard_e92b623cca976c54bce8bcf25a0bedd07.png
    Figura\(\PageIndex{3}\): Gráfica de línea de dos líneas, origen O, con cuadrícula. Eje horizontal, x, escala negativa 4 a 1, por 1s. Eje vertical, y, escala negativa 1 a 4, por 1's Las líneas se cruzan en el punto negativo 2 coma 2.

    En general, un sistema de ecuaciones lineales puede tener:

    • Sin soluciones. En este caso, las líneas que corresponden a cada ecuación nunca se cruzan.
    • Exactamente una solución. Las líneas que corresponden a cada ecuación se cruzan en exactamente un punto.
    • Un número infinito de soluciones. ¡Las gráficas de las dos ecuaciones son la misma línea!

    Entradas en el glosario

    Definición: Sistema de ecuaciones

    Un sistema de ecuaciones es un conjunto de dos o más ecuaciones. Cada ecuación contiene dos o más variables. Queremos encontrar valores para las variables que hagan verdaderas todas las ecuaciones.

    Estas ecuaciones conforman un sistema de ecuaciones:

    \[\left\{\begin{array}{l}{x+y=-2}\\{x-y=12}\end{array}\right.\nonumber\]

    La solución a este sistema es\(x=5\) y\(y=-7\) porque cuando estos valores son sustituidos por\(x\) y\(y\), cada ecuación es verdadera:\(5+(-7)=-2\) y\(5-(-7)=12\).

    Practica

    Ejercicio\(\PageIndex{4}\)

    1. Escribe ecuaciones para las líneas mostradas.

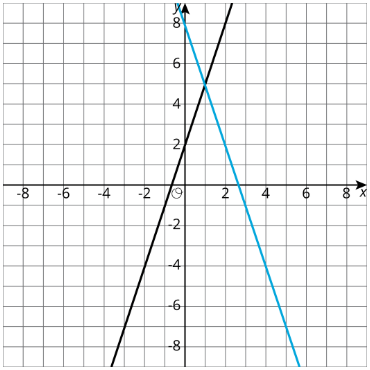
    clipboard_efe9490a33f5d04424da71d52621926d5.png
    Figura\(\PageIndex{4}\): Gráfica de dos líneas que se cruzan en el plano XY. Escala negativa 8 a 8 en ambos ejes. La primera línea se inclinó hacia arriba y hacia la derecha, cruza el eje y en 2, y pasa por el punto 1 coma 5. La segunda línea se inclinó hacia abajo y hacia la derecha, cruza el eje y en 8, y pasa por el punto 1 coma 5.

    2. Describir cómo encontrar la solución al sistema correspondiente mirando la gráfica.

    3. Describir cómo encontrar la solución al sistema correspondiente mediante el uso de las ecuaciones.

    Ejercicio\(\PageIndex{5}\)

    La solución a un sistema de ecuaciones es\((5,-19)\). Elija dos ecuaciones que podrían formar el sistema.

    1. \(y=-3x-6\)
    2. \(y=2x-23\)
    3. \(y=-7x+16\)
    4. \(y=x-17\)
    5. \(y=-2x-9\)

    Ejercicio\(\PageIndex{6}\)

    Resuelve el sistema de ecuaciones:

    \[\left\{\begin{array}{l}{y=4x-3}\\{y=-2x+9}\end{array}\right.\nonumber\]

    Ejercicio\(\PageIndex{7}\)

    Resuelve el sistema de ecuaciones:

    \[\left\{\begin{array}{l}{y=\frac{5}{4}x-2}\\{y=-\frac{1}{4}x+19}\end{array}\right.\nonumber\]

    Ejercicio\(\PageIndex{8}\)

    Aquí hay una ecuación:\(\frac{15(x-3)}{5}=3(2x-3)\)

    1. Resuelve la ecuación usando primero la propiedad distributiva.
    2. Resuelve la ecuación sin usar la propiedad distributiva.
    3. Consulta tu solución.

    (De la Unidad 4.2.5)

    This page titled 4.3.4: Resolver Sistemas de Ecuaciones is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.