Saltar al contenido principal
LibreTexts Español

5.2.2: Tablas, Ecuaciones y Gráficas de Funciones

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118608

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Conectemos ecuaciones y gráficas de funciones.

    Ejercicio\(\PageIndex{1}\): Notice and Wonder: Doubling Back

    ¿Qué notas? ¿Qué te preguntas?

    clipboard_e2bdbbd78d72a8f763a0f55174f7f2df6.png
    Figura\(\PageIndex{1}\): Una gráfica en un plano de coordenadas. Eje horizontal, distancia desde la línea de inicio en metros, eje vertical, tiempo en segundos. La gráfica comienza en el origen y aumenta de manera firme a medida que se mueve hacia la derecha hasta llegar a 200 coma 40. La gráfica luego gira y aumenta de manera constante a medida que se mueve hacia la izquierda hasta llegar al punto 0 coma 74.

    Ejercicio\(\PageIndex{2}\): Equations and Graphs of Functions

    Se muestran las gráficas de tres funciones.

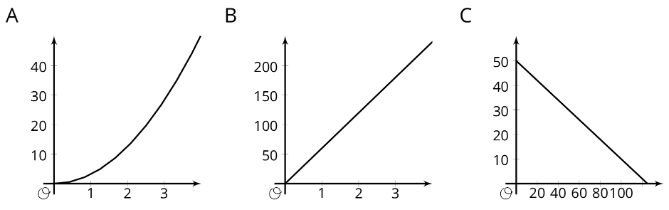
    clipboard_e14f4923f224c6aea2b053de994c4dff1.png
    Figura\(\PageIndex{2}\): Gráficas de 3 funciones. Gráfica A, horizontal 0 a 3 por unos, vertical 0 a 40 por decenas, comenzando en el origen y aumenta, pendiente también aumentando. Gráfica B, horizontal 0 a 3 por unos, vertical o a 200 por cincuenta, comenzando por el origen, la gráfica aumenta linealmente. Gráfica C, horizontal, 0 a 100 por veinte, vertical 0 a 50 por decenas, comenzando en 0 coma 50, disminuye linealmente a 120 coma 0.
    1. Coincidir una de estas ecuaciones con cada una de las gráficas.
      1. \(d=60t\), donde\(d\) es la distancia en millas que recorrías en\(t\) horas si conduces a 60 millas por hora.
      2. \(q=50-0.4d\), donde\(q\) está el número de cuartos, y\(d\) es el número de monedas de diez centavos, en un montón de monedas por valor de 12.50 dólares.
      3. \(A=\pi r^{2}\), donde\(A\) está el área en centímetros cuadrados de un círculo con\(r\) centímetros de radio.
    2. Etiquetar cada uno de los ejes con las variables independientes y dependientes y las cantidades que representan.
    3. Para cada función: ¿Cuál es la salida cuando la entrada es 1? ¿Qué te dice esto sobre la situación? Etiquete el punto correspondiente en la gráfica.
    4. Encuentra dos pares de entrada-salida más. ¿Qué te dicen de la situación? Etiquetar los puntos correspondientes en la gráfica.

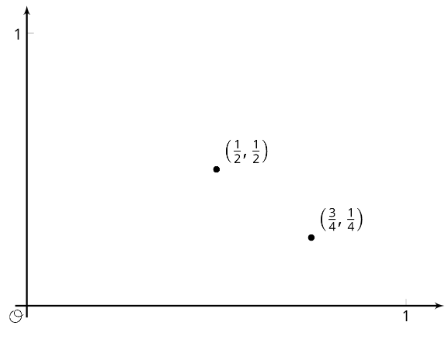
    ¿Estás listo para más?
    Una función ingresa fracciones\(\frac{a}{b}\) entre 0 y 1 donde\(a\) y no\(b\) tienen factores comunes, y genera la fracción\(\frac{1}{b}\). Por ejemplo, dada la entrada las salidas de\(\frac{3}{4}\) la función\(\frac{1}{4}\), y a la entrada las salidas de\(\frac{1}{2}\) la función\(\frac{1}{2}\). Estos dos pares entrada-salida se muestran en la gráfica.

    Traza al menos 10 puntos más en la gráfica de esta función. ¿La mayoría de los puntos de la gráfica están arriba o por debajo de una altura de\(0.3\)? ¿De altura\(0.01\)?

    clipboard_ea0015a632b524569c378c7813ae64f25.png
    Figura\(\PageIndex{3}\)

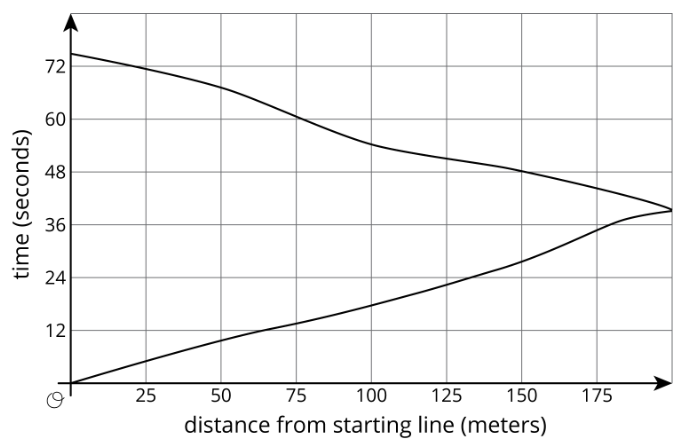
    Ejercicio\(\PageIndex{3}\): Running around a Track

    1. Kiran corría alrededor de la pista. El gráfico muestra el tiempo,\(t\), tardó en correr diversas distancias,\(d\). El cuadro muestra su tiempo en segundos después de cada tres metros.
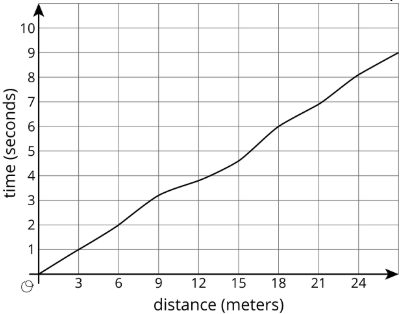
    clipboard_e98ac4e60eab91951ff2d5b09689dffb3.png
    Figura\(\PageIndex{4}\): Gráfica en plano coordenado, eje horizontal, distancia en metros, 0 a 24 por tres, eje vertical, tiempo en segundos, 0 a 10 por unos. La gráfica comienza en el origen y se mueve constantemente hacia arriba y hacia la derecha, pasa a través (3 coma 1) y (18 coma 6).
    \(d\) 0 3 6 9 12 15 18 21 24 27
    \(t\) 0 1.0 2.0 3.2 3.8 4.6 6.0 6.9 8.09 9.0
    Mesa\(\PageIndex{1}\)
    1. ¿Cuánto tiempo le tomó a Kiran correr 6 metros?
    2. ¿Hasta dónde había llegado después de 6 segundos?
    3. Estimar cuándo había corrido 19.5 metros.
    4. Estima hasta dónde corrió en 4 segundos.
    5. ¿El tiempo de Kiran es función de la distancia que ha recorrido? Explica cómo sabes.

    2. Priya corre una vez alrededor de la pista. El gráfico muestra su tiempo dado lo lejos que está de su punto de partida.

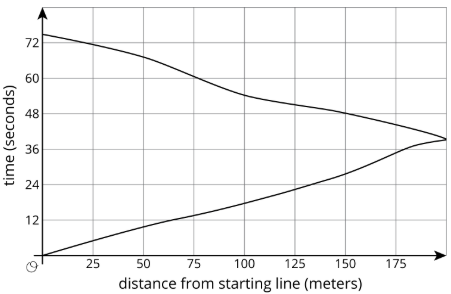
    clipboard_e670c5a3ffb1dcab3ba0398165b9cbb6a.png
    Figura\(\PageIndex{5}\): Una gráfica en un plano de coordenadas. Eje horizontal, distancia desde la línea de inicio en metros, eje vertical, tiempo en segundos. La gráfica comienza en el origen y aumenta de manera firme a medida que se mueve hacia la derecha hasta llegar a 200 coma 40. La gráfica luego gira y aumenta de manera constante a medida que se mueve hacia la izquierda hasta llegar al punto 0 coma 74.
    1. ¿Cuál era su distancia más alejada de su punto de partida?
    2. Estima cuánto tiempo le tomó correr alrededor de la pista.
    3. Estime cuando estaba a 100 metros de su punto de partida.
    4. Estima lo lejos que estaba de la línea de salida después de 60 segundos.
    5. ¿El tiempo de Priya es función de su distancia desde su punto de partida? Explica cómo sabes.

    Resumen

    Aquí está la gráfica que muestra la carrera de Noé.

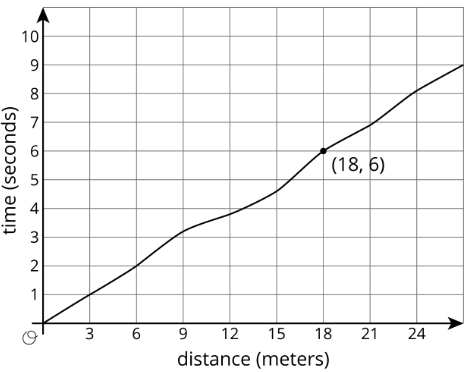
    clipboard_e9068fb7d6587e2b0c64f28d9cff4f547.png
    Figura\(\PageIndex{6}\): Una gráfica en el plano de coordenadas, horizontal, distancia en metros, 0 a 24 por tres, vertical, tiempo en segundos, 0 a 10 por unos. La gráfica comienza en el origen y aumenta constantemente a medida que se mueve hacia la derecha, pasando por el punto etiquetado en (18 coma 6).

    El tiempo en segundos desde que empezó a correr es función de la distancia que ha recorrido. El punto (18,6) de la gráfica te dice que el tiempo que le lleva correr 18 metros es de 6 segundos. La entrada es 18 y la salida es 6.

    El gráfico de una función es todos los pares de coordenadas, (entrada, salida), trazados en el plano de coordenadas. Por convención, siempre ponemos primero la entrada, lo que significa que las entradas se representan en el eje horizontal y las salidas, en el eje vertical.

    Entradas en el glosario

    Definición: Variable dependiente

    Una variable dependiente representa la salida de una función.

    Por ejemplo, supongamos que necesitamos comprar 20 piezas de fruta y decidir comprar manzanas y plátanos. Si seleccionamos primero el número de manzanas, la ecuación\(b=20-a\) muestra el número de plátanos que podemos comprar. El número de plátanos es la variable dependiente porque depende del número de manzanas.

    Definición: Variable independiente

    Una variable independiente representa la entrada de una función.

    Por ejemplo, supongamos que necesitamos comprar 20 piezas de fruta y decidir comprar algunas manzanas y plátanos. Si seleccionamos primero el número de manzanas, la ecuación\(b=20-a\) muestra el número de plátanos que podemos comprar. El número de manzanas es la variable independiente porque podemos elegir cualquier número para ello.

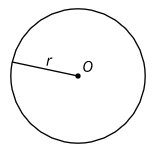
    Definición: Radio

    Un radio es un segmento de línea que va desde el centro hasta el borde de un círculo. Un radio puede ir en cualquier dirección. Cada radio del círculo tiene la misma longitud. También usamos la palabra radio para significar la longitud de este segmento.

    Por ejemplo,\(r\) es el radio de este círculo con centro\(O\).

    clipboard_e69f0a34d6b79fc98f4ba3b0bbc1239b8.png
    Figura\(\PageIndex{7}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

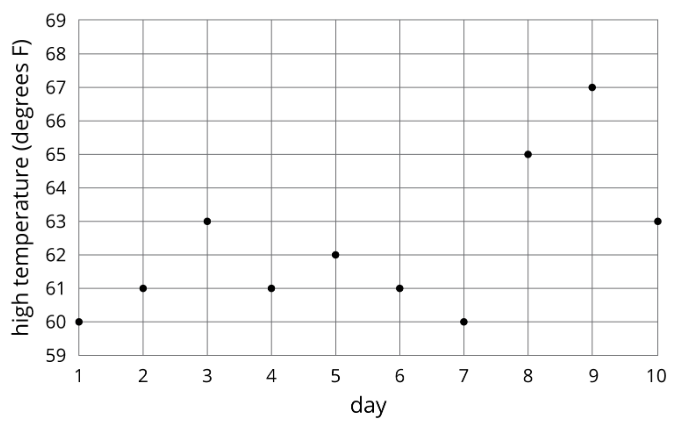
    La gráfica y la tabla muestran las altas temperaturas en una ciudad durante un periodo de 10 días.

    clipboard_eb43b3763aebce8fa4fab3eead04a01e7.png
    Figura\(\PageIndex{8}\)
    día 1 2 3 4 5 6 7 8 9 10
    temperatura (grados F) 60 61 63 61 62 61 60 65 67 63
    Mesa\(\PageIndex{2}\)
    1. ¿Cuál fue la temperatura alta en el Día 7?
    2. ¿En qué días fue la temperatura alta 61 grados?
    3. ¿La alta temperatura es una función del día? Explica cómo sabes.
    4. ¿El día es una función de la alta temperatura? Explica cómo sabes.

    Ejercicio\(\PageIndex{5}\)

    La cantidad que gana la hermana de Lin en su trabajo de medio tiempo es proporcional al número de horas que trabaja. Ella gana $9.60 por hora.

    1. Escribe una ecuación en la forma\(y=kx\) para describir esta situación, donde\(x\) representa las horas que trabaja y\(y\) representa los dólares que gana.
    2. Es\(y\) una función de\(x\)? Explica cómo sabes.
    3. Escribir una ecuación que describa\(x\) como una función de\(y\).

    Ejercicio\(\PageIndex{6}\)

    Usa la ecuación\(2m+4s=16\) para completar la tabla, luego grafica la línea usando\(s\) como variable dependiente.

    \(m\) 0 -2
    \(s\) 3 0
    Mesa\(\PageIndex{3}\)
    clipboard_e3b6834e392125708bd9ef64affe30eee.png
    Figura\(\PageIndex{9}\)

    Ejercicio\(\PageIndex{7}\)

    Resuelve el sistema de ecuaciones:

    \[\left\{\begin{array}{l}{y=7x+10}\\{y=-4x-23}\end{array}\right.\nonumber\]

    (De la Unidad 4.3.4)

    This page titled 5.2.2: Tablas, Ecuaciones y Gráficas de Funciones is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.