Saltar al contenido principal
LibreTexts Español

5.2.3: Más Gráficas de Funciones

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118612

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Lección

    Interpretemos gráficas de funciones.

    Ejercicio\(\PageIndex{1}\): Which One Doesn't Belong: Graphs

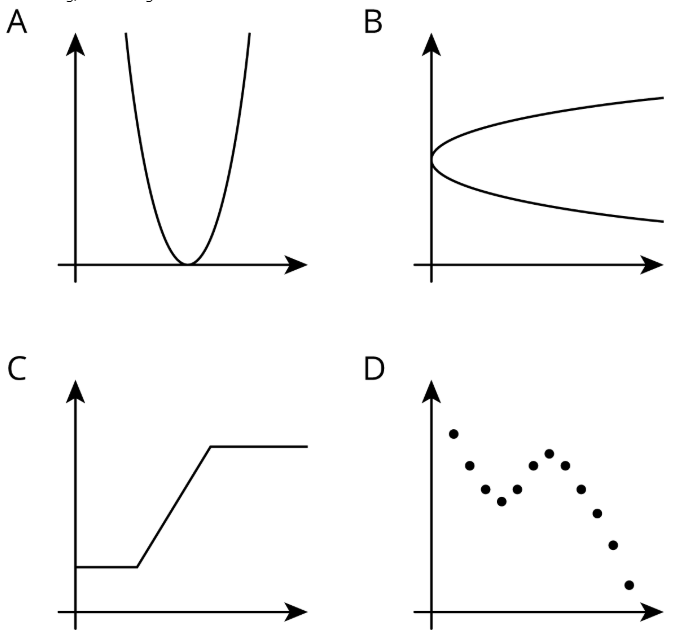
    clipboard_eafb66b89403939652b3cc452fe2ced0f.png
    Figura\(\PageIndex{1}\): Cuatro gráficas, todas cuadrantes 1. Gráfica A, una parábola, abierta, vértice en el eje horizontal. Gráfica B, parábola, abierta a la derecha, vértice en el eje vertical. Gráfica C, gráfica por tramos, constante, pendiente positiva, constante. Gráfica D, diagrama de dispersión, decreciente, creciente, decreciente.

    Ejercicio\(\PageIndex{2}\): Time and Temperature

    La gráfica muestra la temperatura entre el mediodía y la medianoche en un día en una ciudad determinada.

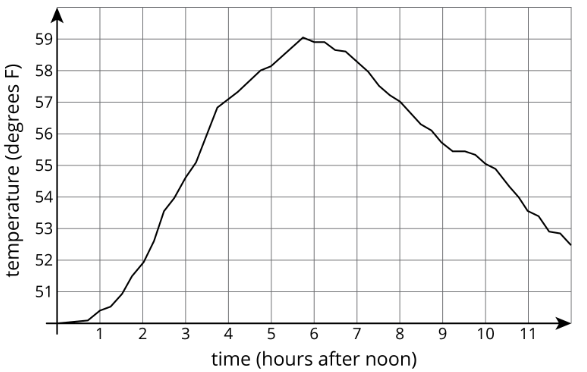
    clipboard_e8ee89b082e3463c76dbc35a8b3b623cf.png
    Figura\(\PageIndex{2}\): Gráfica en plano coordenado, horizontal, tiempo en horas después del mediodía, 0 a 12 por unos, vertical, temperatura en grados Farenheit, 50 a 60 por unos. El gráfico comienza en 0 coma 50 y sube lentamente, más rápido a medida que se mueve hacia la derecha, pasando por 2 coma 52 y 4 coma 57 antes de alcanzar su punto máximo en 5 punto 8 coma 59. La gráfica luego disminuye de manera constante a medida que se mueve hacia la derecha hasta llegar al punto 12 coma 52 punto 5.
    1. ¿Hacía más calor a las 3:00 p.m. o a las 9:00 p.m.?
    2. Aproximadamente ¿cuándo fue la temperatura más alta?
    3. Encuentra otra hora en que la temperatura era la misma que a las 4:00 p.m.
    4. ¿La temperatura cambió más entre la 1:00 p.m. y las 3:00 p.m. o entre las 3:00 p.m. y 5:00 p.m.?
    5. ¿Esta gráfica muestra que la temperatura es una función del tiempo, o el tiempo es una función de la temperatura?
    6. Cuando la entrada para la función es 8, ¿cuál es la salida? ¿Qué te dice eso del tiempo y la temperatura?

    Ejercicio\(\PageIndex{3}\): Garbage

    1. La gráfica muestra la cantidad de basura producida en EU cada año entre 1991 y 2013.
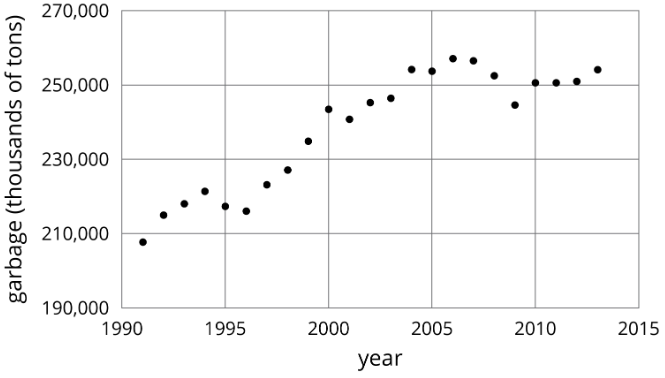
    clipboard_ef1e300fdfd0551bc978d63b8e5bb2e8b.png
    Figura\(\PageIndex{3}\): Gráfica de dispersión, horizontal, año, 1990 a 2015 por cinco, vertical, basura en miles de toneladas, 190,000 a 270 mil por 20,000. Los puntos comienzan en 1991 coma 208,000, y aumentan de manera constante a 2007 coma 255,000 excepto por ligeras disminuciones en 1995 y 2001. Entre 2006 y 2009, los puntos disminuyen, pero vuelven a aumentar de 2009 a 2014.
    1. ¿Aumentó o disminuyó la cantidad de basura entre 1999 y 2000?
    2. ¿Aumentó o disminuyó la cantidad de basura entre 2005 y 2009?
    3. Entre 1991 y 1995, la basura aumentó por tres años, y luego disminuyó en el cuarto año. Describir cómo cambió la cantidad de basura en los años comprendidos entre 1995 y 2000.
    clipboard_ee3db589f412cbe7e28a8e848abfdbf39.png
    Figura\(\PageIndex{4}\): Atribución: Por PublicDomainPictures. Dominio Público. Pixabay. Fuente.

    2. La gráfica muestra el porcentaje de basura que se recicló entre 1991 y 2013.

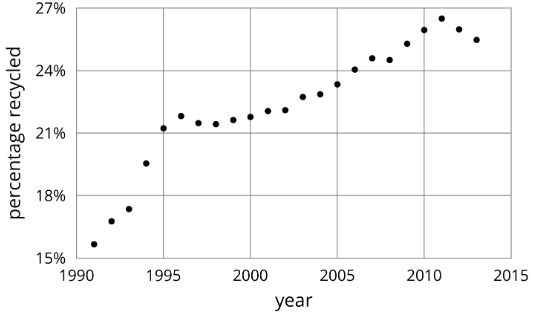
    clipboard_e3a2e5999b1aa16c346fc6aaaea50f297.png
    Figura\(\PageIndex{5}\): Un diagrama de dispersión, horizontal, año, 1900 a 2015 por cincos, vertical, porcentaje reciclado, 15% a 27% por tres. A partir de 1991 coma 16%, los puntos tienen tendencia linealmente ascendente a 1996 coma 22%, luego linealmente al alza a una tasa menos pronunciada a 2011 coma 26%, luego dos puntos tendencia a la baja.
    1. ¿Cuándo iba en aumento?
    2. ¿Cuándo fue disminuyendo?
    3. Cuente la historia del cambio en el porcentaje de basura reciclada en EU durante este periodo de tiempo.

    ¿Estás listo para más?

    Consulte la gráfica en la primera parte de la actividad.

    1. Encuentra un año donde la cantidad de basura producida aumentó con respecto al año anterior, pero no tanto aumentó al año siguiente.
    2. Encontrar un año donde la cantidad de basura producida aumentó con respecto al año anterior, para luego incrementarse en una cantidad menor al año siguiente.
    3. Encuentra un año donde la cantidad de basura producida disminuyó con respecto al año anterior, pero no tanto disminuyó al año siguiente.
    4. Encontrar un año donde la cantidad de basura producida disminuyó con respecto al año anterior, y luego disminuyó en una cantidad menor al año siguiente.

    Resumen

    Aquí hay una gráfica que muestra la temperatura en un pueblo en función del tiempo posterior a las 8:00 p.m.

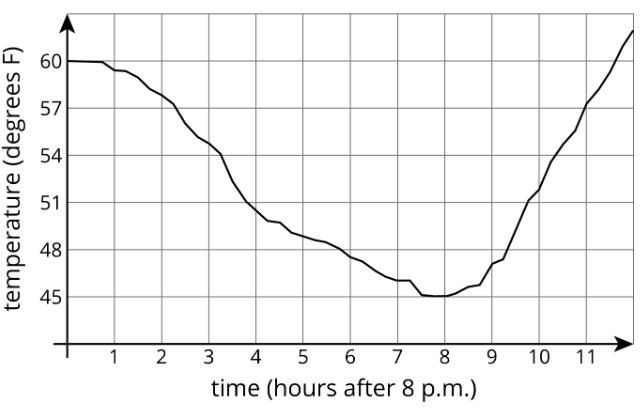
    clipboard_ec0f9d9fa6c50182e64330ea84d5275e5.png
    Figura\(\PageIndex{6}\): La gráfica de una curva en el plano de coordenadas. El eje horizontal se etiqueta como “tiempo en horas después de las 8 pm” y se indican los números del 1 al 11. El eje vertical está etiquetado como “temperatura en grados Fahrenheit” y se indican los números 45 a 60, en incrementos de 3. La curva comienza en el eje vertical en el punto 0 coma 60, y se mueve hacia abajo y hacia la derecha. Continúa hacia abajo hasta alcanzar un punto mínimo de 8 coma 45, gira, y luego se mueve hacia arriba y hacia la derecha, pasando por el punto 11 coma 57.

    La gráfica de una función nos dice lo que está sucediendo en el contexto que representa la función. En este ejemplo, la temperatura inicia en\(60^{\circ}\) F a las 8:00 p.m. Disminuye durante la noche, alcanzando su punto más bajo a las 8 horas después de las 8:00 p.m., o 4:00 a.m. Luego comienza a aumentar nuevamente.

    Entradas en el glosario

    Definición: Variable dependiente

    Una variable dependiente representa la salida de una función.

    Por ejemplo, supongamos que necesitamos comprar 20 piezas de fruta y decidir comprar manzanas y plátanos. Si seleccionamos primero el número de manzanas, la ecuación\(b=20-a\) muestra el número de plátanos que podemos comprar. El número de plátanos es la variable dependiente porque depende del número de manzanas.

    Definición: Variable independiente

    Una variable independiente representa la entrada de una función.

    Por ejemplo, supongamos que necesitamos comprar 20 piezas de fruta y decidir comprar algunas manzanas y plátanos. Si seleccionamos primero el número de manzanas, la ecuación\(b=20-a\) muestra el número de plátanos que podemos comprar. El número de manzanas es la variable independiente porque podemos elegir cualquier número para ello.

    Definición: Radio

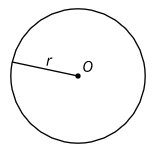
    Un radio es un segmento de línea que va desde el centro hasta el borde de un círculo. Un radio puede ir en cualquier dirección. Cada radio del círculo tiene la misma longitud. También usamos la palabra radio para significar la longitud de este segmento.

    Por ejemplo,\(r\) es el radio de este círculo con centro\(O\).

    clipboard_e69f0a34d6b79fc98f4ba3b0bbc1239b8.png
    Figura\(\PageIndex{7}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

    La solución a un sistema de ecuaciones es\((6,-3)\). Elija dos ecuaciones que podrían formar el sistema.

    1. \(y=-3x+6\)
    2. \(y=2x-9\)
    3. \(y=-5x+27\)
    4. \(y=2x-15\)
    5. \(y=-4x+27\)

    (De la Unidad 4.3.4)

    Ejercicio\(\PageIndex{5}\)

    Un automóvil viaja por una autopista pequeña y va a 55 millas por hora o 35 millas por hora, dependiendo de los límites de velocidad, hasta llegar a su destino a 200 millas de distancia. Dejar\(x\) representar la cantidad de tiempo en horas que el carro va 55 millas por hora, y\(y\) siendo el tiempo en horas que el auto va 35 millas por hora, una ecuación que describe la relación es:\(55x+35y=200\)

    1. Si el auto pasa 2.5 horas yendo 35 millas por hora en el viaje, ¿cuánto tiempo pasa yendo 55 millas por hora?
    2. Si el auto pasa 3 horas yendo 55 millas por hora en el viaje, ¿cuánto tiempo pasa yendo 35 millas por hora?
    3. Si el auto no pasa tiempo yendo 35 millas por hora, ¿cuánto tardaría el viaje? Explica tu razonamiento.

    (De la Unidad 5.2.1)

    Ejercicio\(\PageIndex{6}\)

    La gráfica representa un objeto que es disparado hacia arriba desde una torre y luego cae al suelo. La variable independiente es el tiempo en segundos y la variable dependiente es la altura del objeto sobre el suelo en metros.

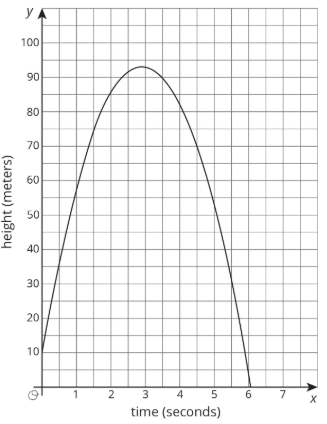
    clipboard_e9209055d679838e87485683c776413d3.png
    Figura\(\PageIndex{8}\): Plano de coordenadas, x, tiempo en segundos, 0 a 7 por unos, y, altura en metros, 0 a 100 por decenas. La gráfica de una curva comienza en (0 coma 10), sube abruptamente a medida que se mueve a la derecha (1 punto 5 coma 75), hasta (2 punto 9 coma 93), luego retrocede a través de (4 punto 5 coma 70), hasta (6 punto 1 coma 0).
    1. ¿Qué tan alta es la torre desde la que se disparó el objeto?
    2. ¿Cuándo chocó el objeto contra el suelo?
    3. Estimar la mayor altura que alcanzó el objeto y el tiempo que tardó en llegar a esa altura. Indicar esta situación en la gráfica.

    This page titled 5.2.3: Más Gráficas de Funciones is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.