5.4.4: Encontrar las dimensiones del cilindro
- Page ID
- 118634
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Averigüemos las dimensiones de los cilindros.
Ejercicio\(\PageIndex{1}\): A Cylinder of Unknown Height
¿Cuál es un volumen posible para este cilindro si el diámetro es de 8 cm? Explica tu razonamiento.
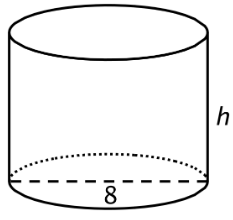
Ejercicio\(\PageIndex{2}\): What's the Dimension?
El volumen\(V\) de un cilindro con radio\(r\) viene dado por la fórmula\(V=\pi r^{2}h\).
1. El volumen de este cilindro con radio 5 unidades es de unidades\(50\pi\) cúbicas. Esta afirmación es cierta:\(50\pi = 5^{2}\pi h\)
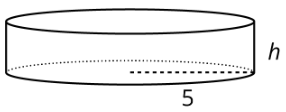
¿Cuál tiene que ser la altura de este cilindro? Explique cómo sabe.
2. El volumen de este cilindro con altura 4 unidades es de unidades\(36\pi\) cúbicas. Esta afirmación es cierta:\(36\pi =4^{2}\pi 4\)
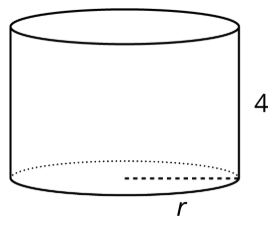
¿Cuál tiene que ser el radio de este cilindro? Explique cómo sabe.
¿Estás listo para más?
Supongamos que un cilindro tiene un volumen de pulgadas\(36\pi\) cúbicas, pero no es el mismo cilindro que el que encontraste anteriormente en esta actividad.
- ¿Cuáles son algunas posibilidades para las dimensiones del cilindro?
- ¿Cuántos cilindros diferentes puedes encontrar que tengan un volumen de pulgadas\(36\pi\) cúbicas?
Ejercicio\(\PageIndex{3}\): Cylinders with Unknown Dimensions
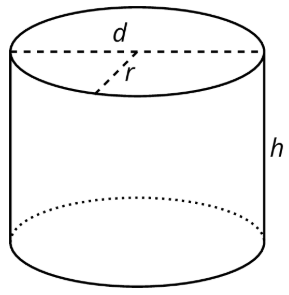
Cada fila de la mesa tiene información sobre un cilindro en particular. Completa la mesa con las dimensiones faltantes.
| diámetro (unidades) | radio (unidades) | área de la base (unidades cuadradas) | altura (unidades) | volumen (unidades cúbicas) |
|---|---|---|---|---|
| 3 | 5 | |||
| 12 | 108\(\pi\) | |||
| 11 | 99\(\pi\) | |||
| 8 | 16\(\pi\) | |||
| 100 | 16\(\pi\) | |||
| 10 | 20\(\pi\) | |||
| 20 | 314 | |||
| \(b\) | \(\pi\cdot b\cdot a^{2}\) |
Resumen
En una lección anterior aprendimos que el volumen,\(V\), de un cilindro con radio\(r\) y altura\(h\) es
\(V=\pi r^{2}h\)
Decimos que el volumen depende del radio y la altura, y si conocemos el radio y la altura, podemos encontrar el volumen. También es cierto que si conocemos el volumen y una dimensión (ya sea radio o altura), podemos encontrar la otra dimensión.
Por ejemplo, imagina un cilindro que tenga un volumen de\(500\pi\) cm 3 y un radio de 5 cm, pero se desconoce la altura. De la fórmula de volumen sabemos que
\(500\pi =\pi\cdot 25\cdot h\)
debe ser verdad. Mirando la estructura de la ecuación, podemos ver eso\(500=25h\). Eso quiere decir que la altura tiene que ser de 20 cm, ya que\(500\div 25=20\).
Ahora imagina otro cilindro que también tenga un volumen de\(500\pi\) cm 3 con un radio desconocido y una altura de 5 cm. Entonces sabemos que
\(500\pi =\pi\cdot r^{2}\cdot 5\)
debe ser verdad. Mirando la estructura de esta ecuación, podemos ver eso. Por lo que el radio debe ser de 10 cm.
Entradas en el glosario
Definición: Cono
Un cono es una figura tridimensional como una pirámide, pero la base es un círculo.
Definición: Cilindro
Un cilindro es una figura tridimensional como un prisma, pero con bases que son círculos.
Definición: Esfera
Una esfera es una figura tridimensional en la que todas las secciones transversales en todas las direcciones son círculos.
Practica
Ejercicio\(\PageIndex{4}\)
Completa la tabla con toda la información que falta sobre tres cilindros diferentes.
| diámetro de la base (unidades) | área de base (unidades cuadradas) | altura (unidades) | volumen (unidades cúbicas) |
|---|---|---|---|
| 4 | 10 | ||
| 6 | 63\(\pi\) | ||
| 25\(\pi\) | 6 |
Ejercicio\(\PageIndex{5}\)
Un cilindro tiene volumen\(45\pi\) y radio 3. ¿Cuál es su altura?
Ejercicio\(\PageIndex{6}\)
Tres cilindros tienen un volumen de 2826 cm 3. El Cilindro A tiene una altura de 900 cm. El Cilindro B tiene una altura de 225 cm. El Cilindro C tiene una altura de 100 cm. Encuentra el radio de cada cilindro. Utilice 3.14 como aproximación para\(\pi\).
Ejercicio\(\PageIndex{7}\)
El camión de reparto de una compañía de gas tiene un tanque cilíndrico de 14 pies de diámetro y 40 pies de largo.
- Esboce el tanque y marque el radio y la altura.
- ¿Cuánto gas puede caber en el tanque?
(De la Unidad 5.4.3)
Ejercicio\(\PageIndex{8}\)
Aquí hay una gráfica que muestra la altura del agua del océano entre el 22 de septiembre y el 24 de septiembre de 2016 en Bodega Bay, CA.
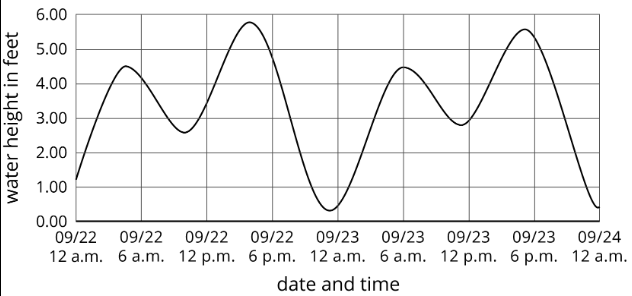
- Estimar la altura del agua a las 12 de la tarde del 22 de septiembre.
- ¿Cuántas veces fue la altura del agua 5 pies? Encuentra dos momentos en los que esto sucede.
- ¿Cuál fue lo más bajo que obtuvo el agua durante este periodo de tiempo? ¿Cuándo ocurre esto?
- ¿Alguna vez el agua alcanza una altura de 6 pies?
(De la Unidad 5.2.3)