5.5.3: Estimación de un hemisferio
- Page ID
- 118600
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Estimemos el volumen de los hemisferios con cifras que conocemos.
Ejercicio\(\PageIndex{1}\): Notice and Wonder: Two Shapes
Aquí hay dos formas.
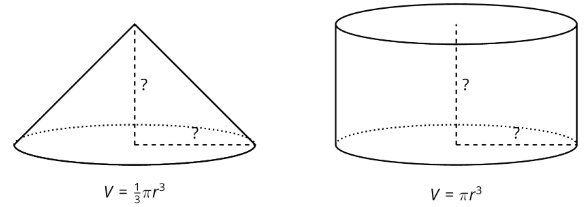
¿Qué notas? ¿Qué te preguntas?
Ejercicio\(\PageIndex{2}\): Hemispheres in Boxes
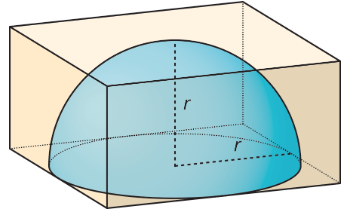
- Mai tiene un pisapapeles de cúpula que puede usar como lupa. El pisapapeles tiene la forma de un hemisferio hecho de vidrio sólido, por lo que quiere diseñar una caja para mantenerlo adentro para que no se rompa. Su pisapapeles tiene un radio de 3 cm.
- ¿Cuáles deben ser las dimensiones del interior de la caja para que la caja sea lo más pequeña posible?
- ¿Cuál es el volumen de la caja?
- ¿Cuál es una estimación razonable para el volumen del pisapapeles?
- Tyler tiene una caja diferente con longitudes laterales que son el doble de largas que los lados de la caja de Mai. La caja de Tyler es lo suficientemente grande como para contener un pisapapeles de vidrio diferente.
- ¿Cuál es el volumen de la nueva caja?
- ¿Cuál es una estimación razonable para el volumen de este pisapapeles de vidrio?
- ¿Cuántas veces más grande crees que es el volumen del pisapapeles en esta caja que el volumen del pisapapeles de Mai? Explica tu forma de pensar.
Ejercicio\(\PageIndex{3}\): Estimating Hemispheres
1. Un hemisferio con radio 5 unidades encaja perfectamente en un cilindro del mismo radio y altura.
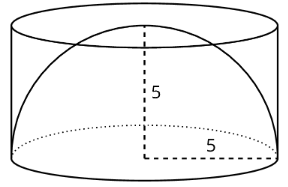
- Calcular el volumen del cilindro.
- Estimar el volumen del hemisferio. Explica tu razonamiento.
2. Un cono encaja perfectamente dentro de un hemisferio, y comparten un radio de 5.
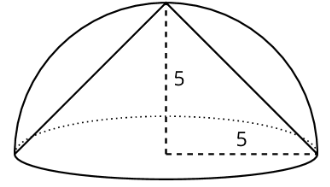
- ¿Cuál es el volumen del cono?
- Estimar el volumen del hemisferio. Explica tu razonamiento.
3. Compara tu estimación para el hemisferio con el cono interior con tu estimación del hemisferio dentro del cilindro. ¿Cómo se comparan con los volúmenes del cilindro y el cono?
¿Estás listo para más?
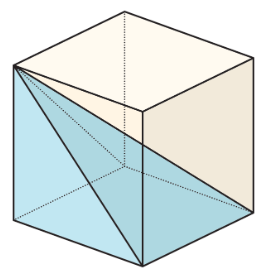
Estimar qué fracción del volumen del cubo está ocupada por la pirámide que comparte la base y un vértice superior con el cubo, como en la figura.
Resumen
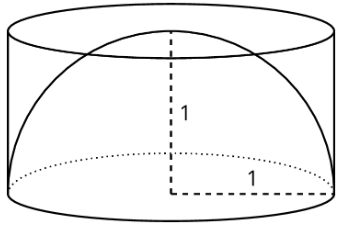
Podemos estimar el volumen de un hemisferio comparándolo con otras formas para las que conocemos el volumen. Por ejemplo, un hemisferio de radio 1 unidad encaja dentro de un cilindro con un radio de 1 unidad y una altura de 1 unidad.
Dado que el hemisferio está dentro del cilindro, debe tener un volumen menor que el cilindro, lo que hace que el volumen del cilindro sea una sobreestimación razonable para el volumen del hemisferio.
El volumen de este cilindro en particular es de alrededor de 3.14 unidades 3 ya que\(\pi (1)^{2}(1)=\pi\), así sabemos que el volumen del hemisferio es menor a 3.14 unidades cúbicas.
Usando lógica similar, un cono de radio 1 unidad y altura 1 unidad encaja dentro del hemisferio de radio 1 unidad.
Dado que el cono está dentro del hemisferio, el cono debe tener un volumen menor que el hemisferio, lo que hace que el volumen del cono sea una subestimación razonable para el volumen del hemisferio.
El volumen de este cono en particular es de aproximadamente 1.05 unidades 3 ya que\(\frac{1}{3}\pi (1)^{2}(1)=\frac{1}{3}\pi\approx 1.05\), por lo que sabemos que el volumen del hemisferio es de más de 1.05 unidades cúbicas.
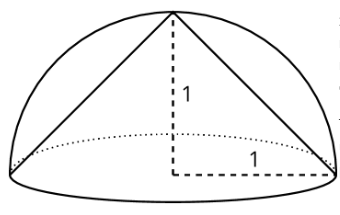
Al promediar los volúmenes del cilindro y el cono, podemos estimar que el volumen del hemisferio sea de aproximadamente 2.10 unidades 3 ya que\(\frac{3.14+1.05}{2}\approx 2.10\). Y, dado que un hemisferio es la mitad de una esfera, también podemos estimar que una esfera con radio de 1 sería el doble de este volumen, o alrededor de 4.20 unidades 3.
Practica
Ejercicio\(\PageIndex{4}\)
Una pelota de béisbol se ajusta perfectamente dentro de un cubo de exhibición transparente. La longitud de un borde del cubo es de 2.9 pulgadas.
¿El volumen del beisbol es mayor, menor o igual a pulgadas\(2.9^{3}\) cúbicas? Explique cómo sabe.