6.2.2: Ajuste de una Línea a Datos

Lección

Veamos las gráficas de dispersión en su conjunto.

Ejercicio\(\PageIndex{1}\): Predict This

Aquí hay un diagrama de dispersión que muestra pesos y eficiencias de combustible de 20 tipos diferentes de automóviles.

Figura\(\PageIndex{1}\)

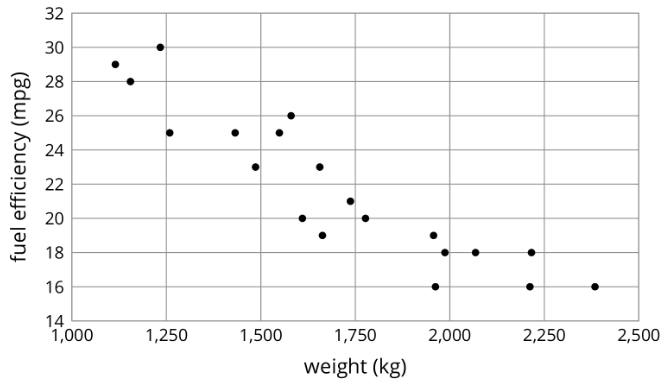
Si un automóvil pesa 1,750 kg, ¿esperaría que su eficiencia de combustible esté más cerca de 22 mpg o de 28 mpg? Explica tu razonamiento.

Ejercicio\(\PageIndex{2}\): Shine Bright

Aquí hay una tabla que muestra pesos y precios de 20 diamantes diferentes.

Mesa\(\PageIndex{1}\)

peso (quilates)	precio real (dólares)	precio previsto (dólares)
1	3,772	4,429
1	4,221	4,429
1	4,032	4,429
1	5,385	4,429
1.05	3,942	4,705
1.05	4,480	4,705
1.06	4,511	4,760
1.2	5,544	5533
1.3	6,131	6,085
1.32	5,872	6,195
1.41	7,122	6,692
1.5	7,474	7,189
1.5	5,904	7,189
1.59	8,706	7,686
1.61	8,252	7,796
1.73	9,530	8,459
1.77	9,374	8,679
1.85	8,169	9,121
1.9	9,541	9,397
2.04	9,125	10,170

El diagrama de dispersión muestra los precios y pesos de los 20 diamantes junto con la gráfica de\(y=5,520x-1,091\).

La función descrita por la ecuación\(y=5,520x-1,091\) es un modelo de la relación entre el peso de un diamante y su precio.

Este modelo predice el precio de un diamante a partir de su peso. Estos precios previstos se muestran en la tercera columna de la tabla.

1. Dos diamantes que pesan 1.5 quilates tienen diferentes precios. ¿Cuáles son sus precios? ¿Cómo puedes ver esto en la tabla? ¿Cómo puedes ver esto en la gráfica?
2. El modelo predice que cuando el peso es de 1.5 quilates, el precio será de $7,189. ¿Cómo puedes ver esto en la gráfica? ¿Cómo puedes ver esto usando la ecuación?
3. Uno de los diamantes pesa 1.9 quilates. ¿Qué predice el modelo para su precio? ¿Cómo se compara eso con el precio real?
4. Encuentra un diamante para el que el modelo haga una muy buena predicción del precio real. ¿Cómo puedes ver esto en la tabla? ¿En la gráfica?
5. Encuentra un diamante para el que la predicción del modelo no esté muy cerca del precio real. ¿Cómo puedes ver esto en la tabla? ¿En la gráfica?

Ejercicio\(\PageIndex{3}\): The Agony of the Feet

Aquí hay una gráfica de dispersión que muestra longitudes y anchuras de 20 pies izquierdos diferentes. Usa las flechas dobles para mostrar u ocultar la lista de expresiones.

1. Estimar los anchos del pie más largo y el pie más corto.
2. Estimar las longitudes del pie más ancho y el pie más estrecho.
3. Haga clic en el círculo gris junto a las palabras “La Línea” en la lista de expresiones. Debe aparecer la gráfica de un modelo lineal. Encuentra el punto de datos que parece raro al compararlo con el modelo. ¿Qué longitud y anchura representa ese punto?

Resumen

En ocasiones, podemos usar una función lineal como modelo de la relación entre dos variables. Por ejemplo, aquí hay una gráfica de dispersión que muestra las alturas y pesos de 25 perros junto con la gráfica de una función lineal que es un modelo para la relación entre la altura de un perro y su peso.

Figura\(\PageIndex{2}\)

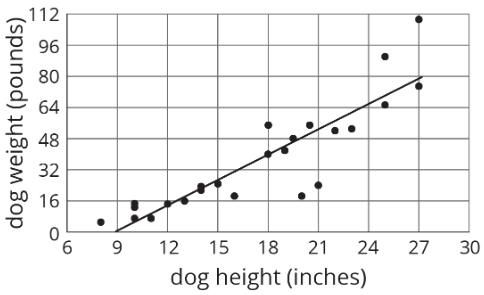
Podemos ver que el modelo hace un buen trabajo al predecir el peso dada la altura para algunos perros. Estos corresponden a puntos en o cerca de la línea. El modelo no hace muy buen trabajo al predecir el peso dada la altura para los perros cuyos puntos están lejos de la línea.

Por ejemplo, hay un perro que mide aproximadamente 20 pulgadas de alto y pesa un poco más de 16 libras. El modelo predice que el peso sería de unas 48 libras. Decimos que el modelo sobrepredice el peso de este perro. También hay un perro que mide 27 pulgadas de alto y pesa alrededor de 110 libras. El modelo predice que su peso será un poco menos de 80 libras. Decimos que el modelo subpredice el peso de este perro.

A veces un punto de datos está muy lejos de los otros puntos o no se ajusta a una tendencia que todos los demás puntos encajan. A estos valores atípicos los llamamos.

Entradas en el glosario

Definición: Outlier

Un valor atípico es un valor de datos que está lejos de los otros valores en el conjunto de datos.

Aquí hay una gráfica de dispersión que muestra longitudes y anchuras de 20 pies izquierdos diferentes. El pie cuya longitud es de 24.5 cm y ancho es de 7.8 cm es un valor atípico.

Figura\(\PageIndex{3}\)

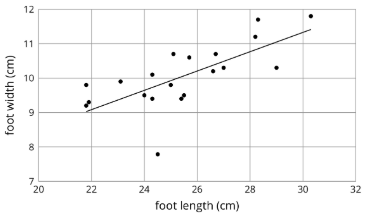
Practica

Ejercicio\(\PageIndex{4}\)

El diagrama de dispersión muestra el número de hits y jonrones para 20 beisbolistas que tuvieron al menos 10 hits la temporada pasada. En la tabla se muestran los valores para 15 de esos jugadores.

El modelo, representado por\(y=0.15x-1.5\), se grafica con un diagrama de dispersión.

Figura\(\PageIndex{4}\)

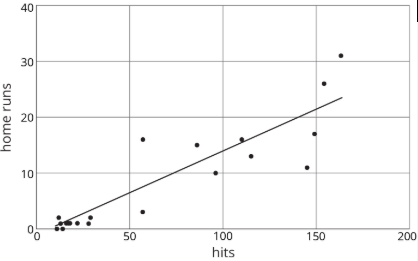
hits	jonrones	jonrones predichos
12	2	0.3
22	1	1.8
154	26	21.6
145	11	20.3
110	16	15
57	3	7.1
149	17	20.9
29	2	2.9
13	1	0.5
18	1	1.2
86	15	11.4
163	31	23
115	13	15.8
57	16	7.1
96	10	12.9

Mesa\(\PageIndex{2}\)

Utilice la gráfica y la tabla para responder a las preguntas.

1. El jugador A tuvo 154 hits en 2015. ¿Cuántos jonrones tenía? ¿Cuántos se predijo que tendría?
2. El jugador B fue el jugador que más superó a la predicción. ¿Cuántos hits tuvo el Jugador B la temporada pasada?
3. ¿Qué esperarías ver en la gráfica para un jugador que bateó muchos menos jonrones de los que predijo el modelo?

Ejercicio\(\PageIndex{5}\)

Aquí hay una gráfica de dispersión que compara puntos por juego con intentos de tiros libres por juego para jugadores de basquetbol en un torneo. El modelo, representado por\(y=4.413x+0.377\), se grafica con el diagrama de dispersión. Aquí,\(x\) representa intentos de tiros libres por juego, y\(y\) representa puntos por juego.

Figura\(\PageIndex{5}\)

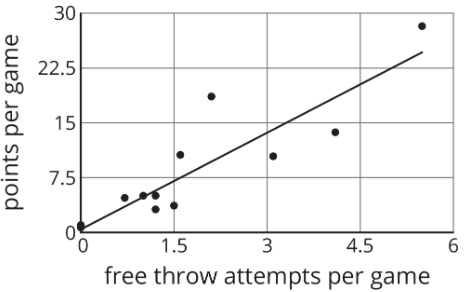
1. Encierra en círculo cualquier punto de datos que parezcan ser valores atípicos.
2. ¿Qué significa que un punto esté muy por encima de la línea en esta situación?
3. Basado en el modelo, ¿cuántos puntos por juego esperarías que tuviera un jugador que intente 4.5 tiros libres por juego? Redondear su respuesta a la décima de punto más cercana por juego.
4. Uno de los jugadores anotó 13.7 puntos por juego con 4.1 intentos de tiros libres por juego. ¿Cómo se compara esto con lo que el modelo predice para este jugador?