6.2.4: La pendiente de una línea ajustada
- Page ID
- 118760
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Veamos cómo cambiar una variable cambia a otra.
Ejercicio\(\PageIndex{1}\): Estimating Slope
Estimar la pendiente de la línea.
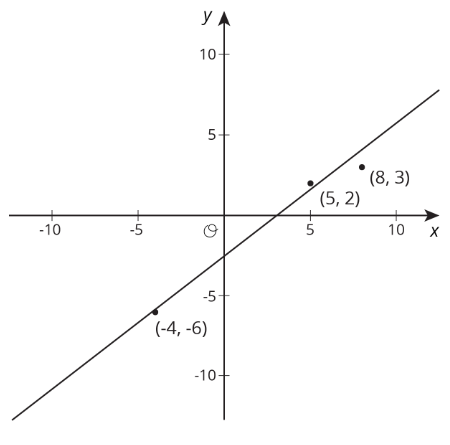
Ejercicio\(\PageIndex{2}\): Describing Linear Associations
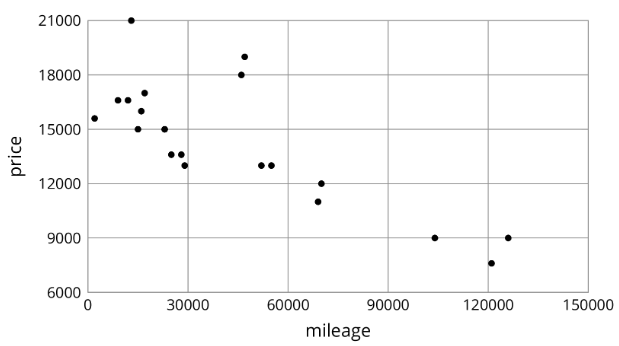
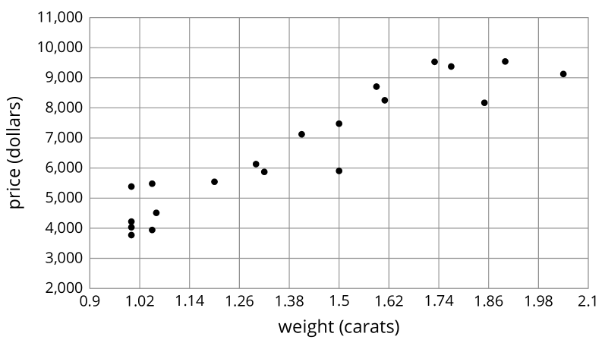
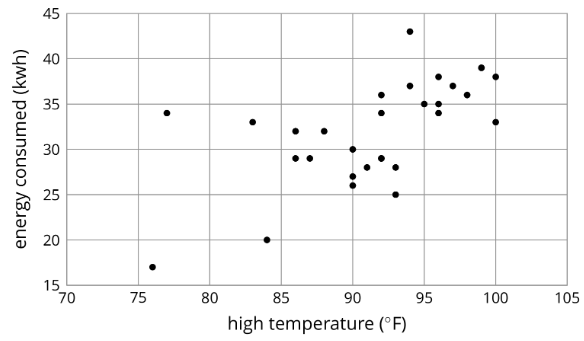
Para cada diagrama de dispersión, decida si existe una asociación entre las dos variables y describa la situación usando una de estas frases:
- Para estos datos, a medida que ________________ aumenta, ________________ tiende a aumentar.
- Para estos datos, a medida que ________________ aumenta, ________________ tiende a disminuir.
- Para estos datos, ________________ y ________________ no parecen estar relacionados.
Ejercicio\(\PageIndex{3}\): Interpreting Slopes
Para cada una de las situaciones se muestra un modelo lineal para algunos datos.
- ¿Cuál es la pendiente de la línea en el diagrama de dispersión para cada situación?
- ¿Cuál es el significado de la pendiente en esa situación?
\(y=5,520.619x - 1,091.393\)
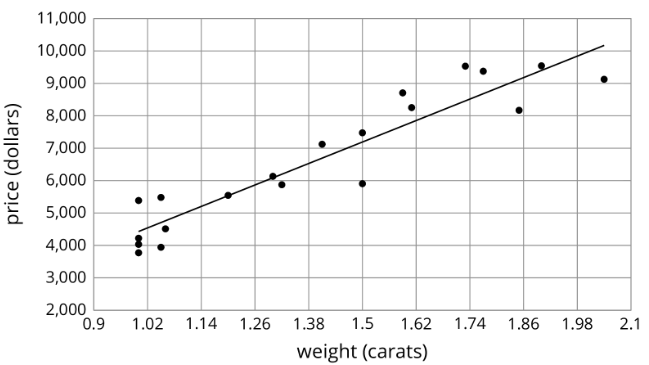
\(y=-.011x + 40.604\)
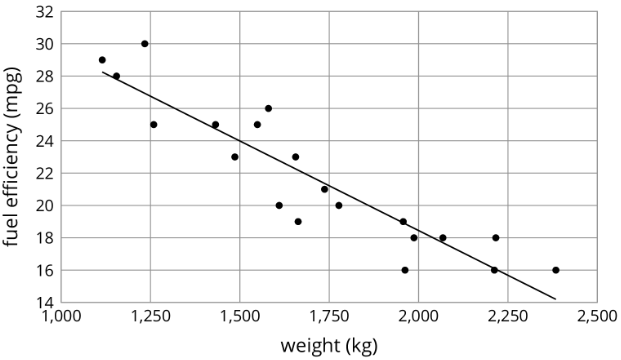
\(y=0.59x - 21.912\)
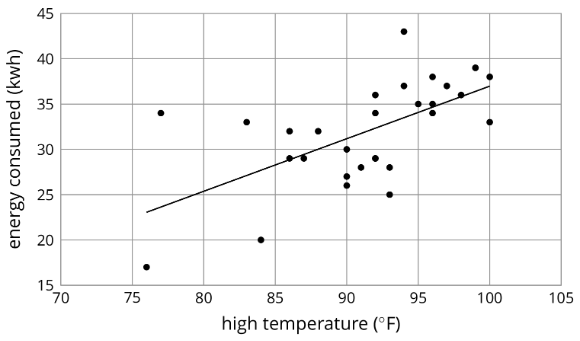
¿Estás listo para más?
La gráfica de dispersión muestra los datos de peso y eficiencia de combustible utilizados en una lección anterior junto con un modelo lineal representado por la ecuación\(y = -0.0114x + 41.3021\)
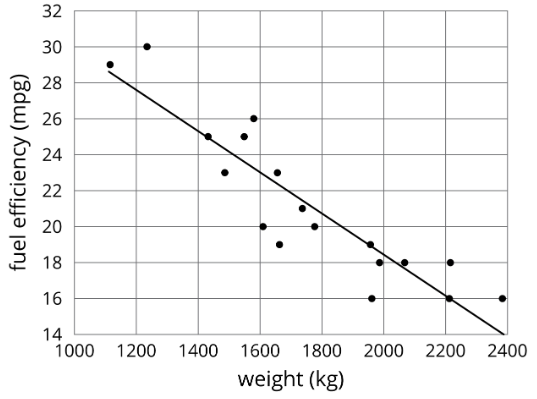
- ¿Cuál es el valor de la pendiente y qué significa en este contexto?
- ¿Qué representa el otro número de la ecuación en la gráfica? ¿Qué significa en contexto?
- Utilice la ecuación para predecir la eficiencia de combustible de un automóvil que pesa 100 kilogramos.
- Utilice la ecuación para predecir el peso de un automóvil que tenga una eficiencia de combustible de 22 mpg.
- ¿Cuál de estas dos predicciones probablemente se ajusta mejor a la realidad? Explicar.
Ejercicio\(\PageIndex{4}\): Positive or Negative?
1. Para cada una de las gráficas de dispersión, decida si tiene sentido ajustar un modelo lineal a los datos. Si lo hace, ¿la gráfica del modelo tendría una pendiente positiva, una pendiente negativa o una pendiente de cero?
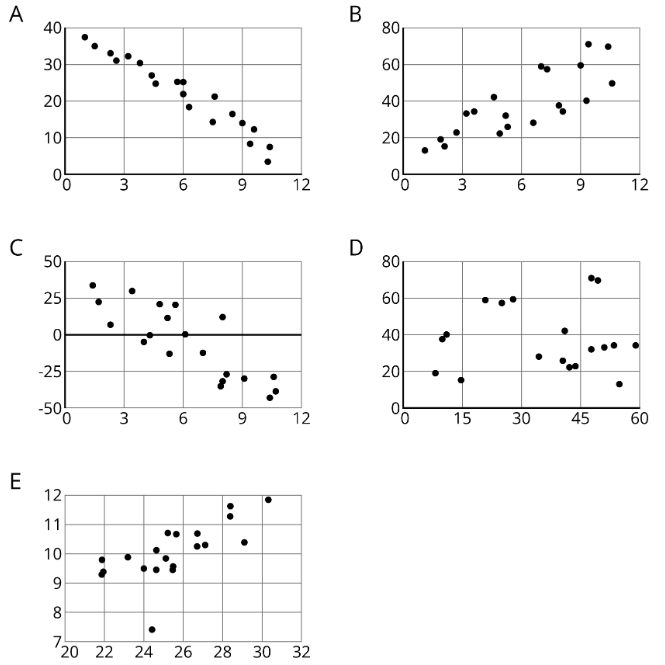
2. ¿Cuáles de estas gráficas de dispersión muestran evidencia de una asociación positiva entre las variables? ¿De una asociación negativa? ¿Cuáles no parecen mostrar una asociación?
Resumen
Aquí hay un diagrama de dispersión que hemos visto antes. Como se señaló anteriormente, podemos ver en el diagrama de dispersión que los perros más altos tienden a pesar más que los perros más cortos. Otra forma de decirlo es que el peso tiende a aumentar a medida que aumenta la altura. Cuando tenemos una asociación positiva entre dos variables, un aumento en una significa que tiende a haber un aumento en la otra.
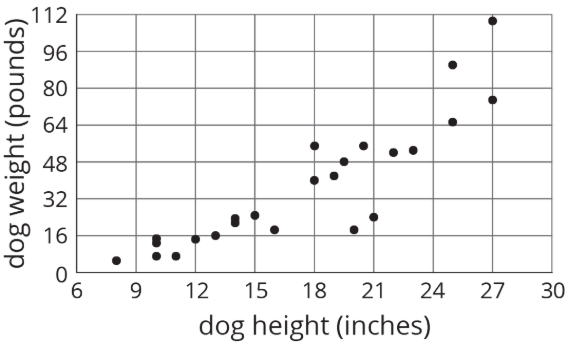
Podemos cuantificar esta tendencia ajustando una línea a los datos y encontrando su pendiente. Por ejemplo, la ecuación de la línea ajustada es\(w=4.27h-37\) donde\(h\) está la altura del perro y\(w\) es el peso previsto del perro.
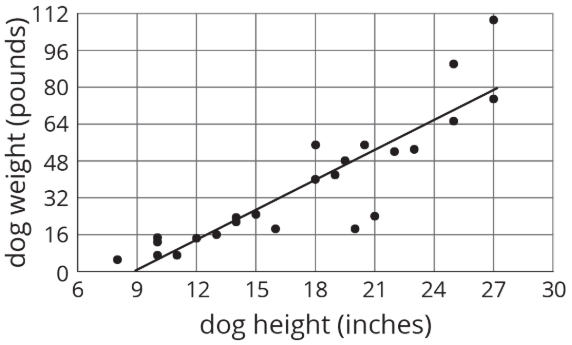
El desnivel es de 4.27, lo que nos dice que por cada incremento de 1 pulgada en la altura del perro, se prevé que el peso aumente en 4.27 libras.
En nuestro ejemplo de la eficiencia de combustible y el peso de un automóvil, la pendiente de la línea ajustada mostrada es -0.01.
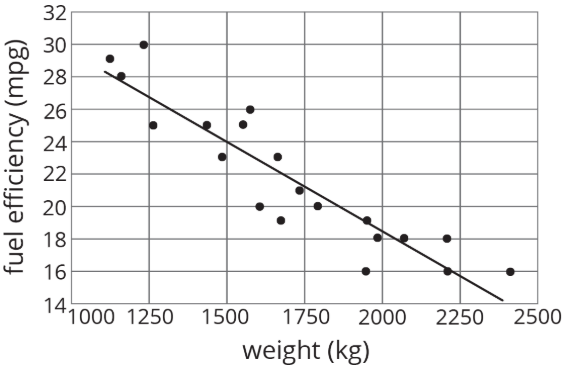
Esto nos dice que por cada incremento de 1 kilogramo en el peso del automóvil, se prevé que la eficiencia del combustible disminuya en 0.01 millas por galón. Cuando tenemos una asociación negativa entre dos variables, un aumento en una significa que tiende a haber una disminución en la otra.
Entradas en el glosario
Definición: Asociación Negativa
Una asociación negativa es una relación entre dos cantidades donde una tiende a disminuir a medida que la otra aumenta. En una gráfica de dispersión, los puntos de datos tienden a agruparse alrededor de una línea con pendiente negativa.
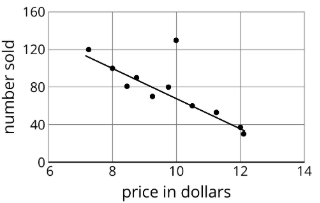
Diferentes tiendas en todo el país venden un libro por diferentes precios.
El diagrama de dispersión muestra que existe una asociación negativa entre el precio del libro en dólares y el número de libros vendidos a ese precio.
Definición: Outlier
Un valor atípico es un valor de datos que está lejos de los otros valores en el conjunto de datos.
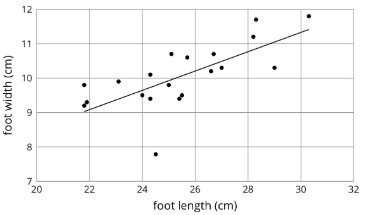
Aquí hay una gráfica de dispersión que muestra longitudes y anchuras de 20 pies izquierdos diferentes. El pie cuya longitud es de 24.5 cm y ancho es de 7.8 cm es un valor atípico.
Definición: Asociación Positiva
Una asociación positiva es una relación entre dos cantidades donde una tiende a aumentar a medida que la otra aumenta. En una gráfica de dispersión, los puntos de datos tienden a agruparse alrededor de una línea con pendiente positiva.
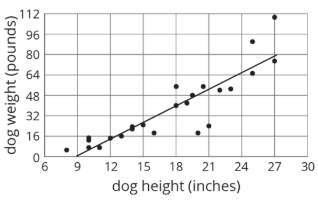
La relación entre altura y peso para 25 perros se muestra en el diagrama de dispersión. Existe una asociación positiva entre la altura del perro y el peso del perro.
Práctica
Ejercicio\(\PageIndex{5}\)
¿Cuál de estas afirmaciones es cierta sobre los datos en el diagrama de dispersión?
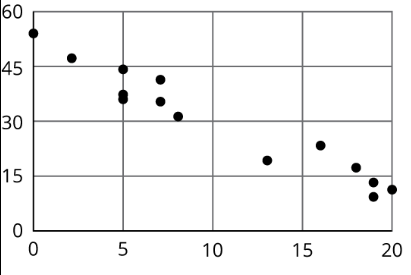
- A\(x\) medida que aumenta,\(y\) tiende a aumentar.
- A\(x\) medida que aumenta,\(y\) tiende a disminuir.
- A medida que\(x\) aumenta,\(y\) tiende a permanecer sin cambios.
- \(x\)y no\(y\) están relacionados.
Ejercicio\(\PageIndex{6}\)
Aquí hay un diagrama de dispersión que compara los golpes con los murciélagos para los jugadores de un equipo de béisbol.
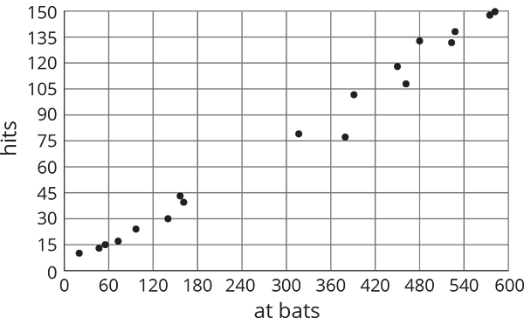
Describir la relación entre el número de murciélagos y el número de aciertos utilizando los datos del diagrama de dispersión.
Ejercicio\(\PageIndex{7}\)
El modelo lineal para algunos datos de mariposa viene dado por la ecuación\(y=0.238x+4.642\). ¿Cuál de los siguientes describe mejor la pendiente del modelo?
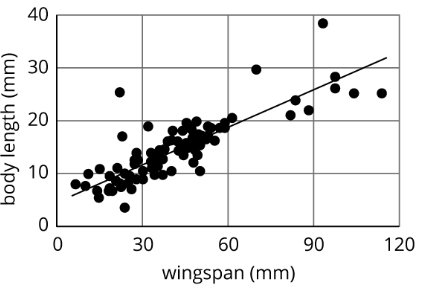
- Por cada 1 mm la envergadura aumenta, la longitud de la mariposa aumenta 0.238 mm.
- Por cada 1 mm la envergadura aumenta, la longitud de la mariposa aumenta 4.642 mm.
- Por cada 1 mm la longitud de la mariposa aumenta, la envergadura aumenta 0.238 mm.
- Por cada 1 mm la longitud de la mariposa aumenta, la envergadura aumenta 4.642 mm.
Ejercicio\(\PageIndex{8}\)
En el gráfico de dispersión se muestran los horarios de los vuelos sin escalas, de solo ida del Aeropuerto O'Hare en Chicago y los precios de un boleto de ida.
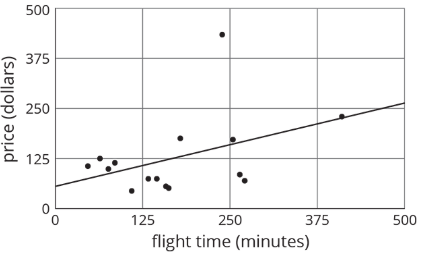
- Encierra en círculo cualquier dato que parezca ser valores atípicos.
- Utilice la gráfica para estimar la diferencia entre los valores atípicos y sus valores predichos.
(De la Unidad 6.2.2)
Ejercicio\(\PageIndex{9}\)
Resolver:
\[\left\{\begin{array}{l}{y=-3x+13}\\{y=-2x+1}\end{array}\right.\nonumber\]
(De la Unidad 4.3.5)