Saltar al contenido principal
LibreTexts Español

6.2.5: Observando más patrones en gráficas de dispersión

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118756

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Busquemos otros patrones en los datos.

    Ejercicio\(\PageIndex{1}\): Notice and Wonder: Nonlinear Scatter Plot

    ¿Qué notas? ¿Qué te preguntas?

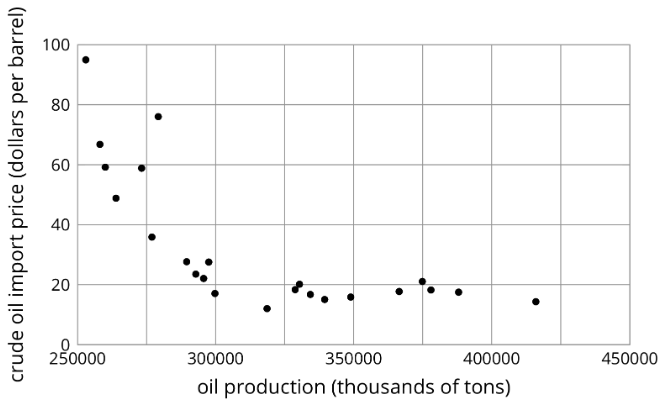
    clipboard_ee3007b60d55efbd80bfed2700239c491.png
    Figura\(\PageIndex{1}\)

    Ejercicio\(\PageIndex{2}\): Scatter Plot City

    Tu profesor te dará un juego de tarjetas. Cada carta muestra un diagrama de dispersión.

    1. Clasifique las tarjetas en categorías y describa cada categoría.
    2. Explique el razonamiento detrás de sus categorías a su pareja. Escucha el razonamiento de tu pareja para sus categorías.
    3. Clasifique las tarjetas en dos categorías: asociaciones positivas y asociaciones negativas. Compara tu clasificación con la de tu pareja y discute cualquier desacuerdo.
    4. Clasifique las tarjetas en dos categorías: asociaciones lineales y asociaciones no lineales. Compara tu clasificación con la de tu pareja y discute cualquier desacuerdo.

    Ejercicio\(\PageIndex{3}\): Clustering

    ¿En qué se parecen estas gráficas de dispersión? ¿En qué se diferencian?

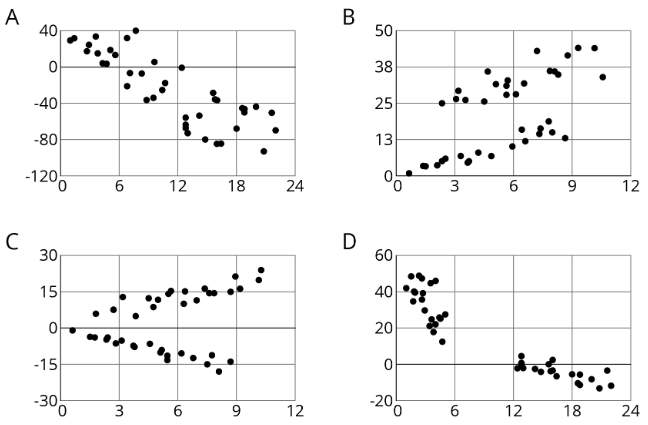
    clipboard_ebedcb22e09ced0ee912f6fcabc43a67f.png
    Figura\(\PageIndex{2}\): Cuatro diagramas de dispersión. Trama A, los puntos comienzan en 0 coma 40 y tienden a la baja y a la derecha. La parcela B tiene 2 juegos de puntos, 1 comienza cerca del origen y tiende hacia arriba y hacia la derecha. El segundo comienza cerca de 3 coma 25 y tiende hacia arriba y hacia la derecha. La parcela C tiene 2 juegos de puntos, 1 comienza cerca del origen y tiende hacia arriba y hacia la derecha. El segundo comienza cerca del origen y tiende hacia abajo y hacia la derecha. Los puntos de la trama D comienzan cerca de 0 coma 40 y tienden a la baja y a la derecha hacia 24 negativos 20, pero no hay puntos entre x = 6 y x = 12.

    Resumen

    A veces, una gráfica de dispersión muestra una asociación que no es lineal:

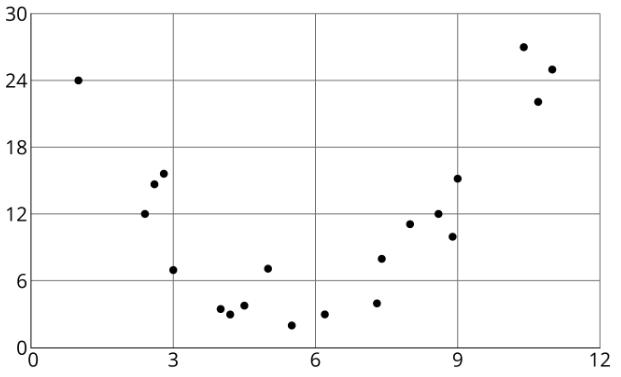
    clipboard_e10463cd08199ff51554d66e65a108485.png
    Figura\(\PageIndex{3}\)

    Llamamos a tal asociación asociación no lineal. En grados posteriores, estudiarás funciones que pueden ser modelos para asociaciones no lineales.

    A veces en una gráfica de dispersión podemos ver grupos separados de puntos.

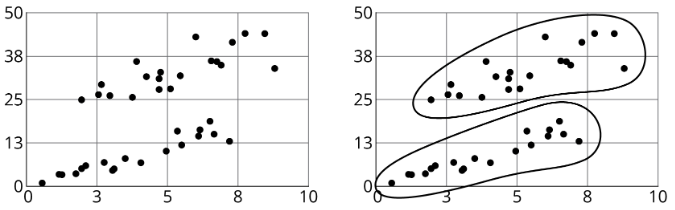
    clipboard_e522959635f2a9ad5635ab81f30608313.png
    Figura\(\PageIndex{4}\): Un diagrama de dispersión con dos grupos de puntos. El primero comienza cerca del origen y tiende hacia arriba y hacia la derecha hacia 8 coma 13. El segundo grupo comienza cerca de 3 coma 25 y tiende hacia arriba y derecha hacia 9 coma 45. La segunda imagen es la misma gráfica de dispersión, con cada grupo en un círculo.

    A estos grupos los llamamos clusters.

    Entradas en el glosario

    Definición: Asociación Negativa

    Una asociación negativa es una relación entre dos cantidades donde una tiende a disminuir a medida que la otra aumenta. En una gráfica de dispersión, los puntos de datos tienden a agruparse alrededor de una línea con pendiente negativa.

    Diferentes tiendas en todo el país venden un libro por diferentes precios.

    El diagrama de dispersión muestra que existe una asociación negativa entre el precio del libro en dólares y el número de libros vendidos a ese precio.

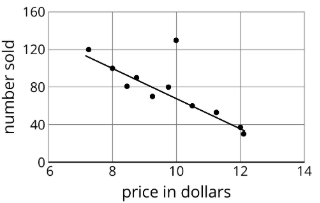
    clipboard_eab65766890cf1492613cd690560b3992.png
    Figura\(\PageIndex{5}\)

    Definición: Outlier

    Un valor atípico es un valor de datos que está lejos de los otros valores en el conjunto de datos.

    Aquí hay una gráfica de dispersión que muestra longitudes y anchuras de 20 pies izquierdos diferentes. El pie cuya longitud es de 24.5 cm y ancho es de 7.8 cm es un valor atípico.

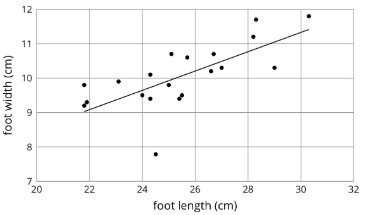
    clipboard_e8c41b607f7acd2fad49b581c0621199d.png
    Figura\(\PageIndex{6}\)

    Definición: Asociación Positiva

    Una asociación positiva es una relación entre dos cantidades donde una tiende a aumentar a medida que la otra aumenta. En una gráfica de dispersión, los puntos de datos tienden a agruparse alrededor de una línea con pendiente positiva.

    La relación entre altura y peso para 25 perros se muestra en el diagrama de dispersión. Existe una asociación positiva entre la altura del perro y el peso del perro.

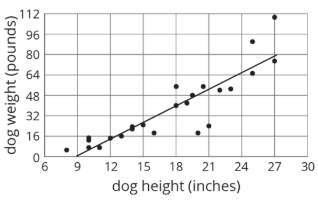
    clipboard_ee59595d412dd9cac9e902713a4d8844c.png
    Figura\(\PageIndex{7}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

    La tasa de alfabetización y la población de los 12 países con más de 100 millones de personas se muestran en el diagrama de dispersión. Encierra en círculo cualquier clúster en los datos.

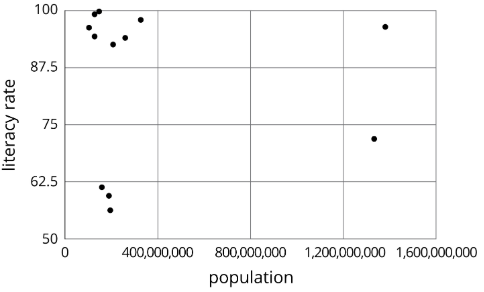
    clipboard_e683748760afe218d8eb1901cecd0ccf9.png
    Figura\(\PageIndex{8}\)

    Ejercicio\(\PageIndex{5}\)

    Aquí hay un diagrama de dispersión:

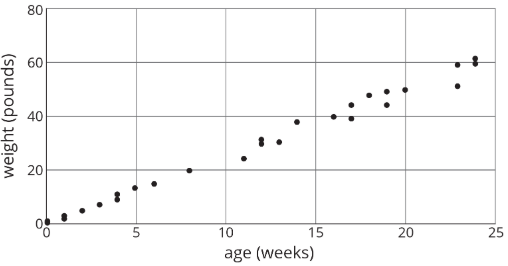
    clipboard_e74bf16b84ac701511f45c11bc38e028c.png
    Figura\(\PageIndex{9}\)

    Seleccione todas las siguientes opciones que describan la asociación en el diagrama de dispersión:

    1. Asociación lineal
    2. Asociación no lineal
    3. Asociación positiva
    4. Asociación negativa
    5. Sin asociación

    Ejercicio\(\PageIndex{6}\)

    Para los mismos datos, se grafican dos modelos diferentes. ¿Qué modelo coincide más con los datos? Explica tu razonamiento.

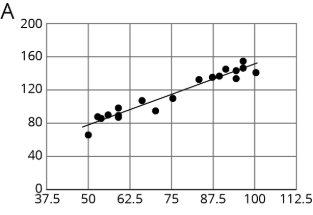
    clipboard_e295e89491ba587383d89b8beceaedb29.png
    Figura\(\PageIndex{10}\)
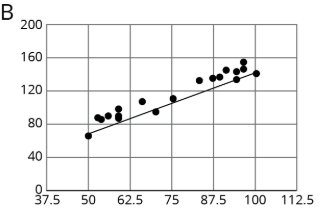
    clipboard_e25660d29960fa4cab185f07ece84f131.png
    Figura\(\PageIndex{11}\)

    (De la Unidad 6.2.3)

    Ejercicio\(\PageIndex{7}\)

    Aquí hay un diagrama de dispersión de datos para algunas de las montañas más altas de la Tierra.

    Se muestran las alturas en metros y año de primer ascenso registrado. El monte Everest es la montaña más alta de este conjunto de datos.

    1. Estimar la altura del Monte Everest.
    2. Estimar el año del primer ascenso registrado del Monte Everest.
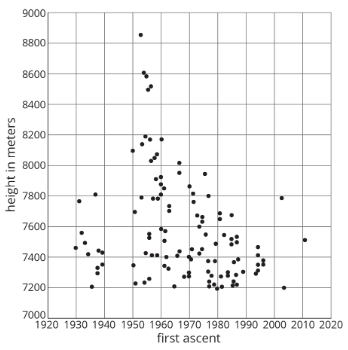
    clipboard_e3c69564ab18f82edf3877aefab7f6eb6.png
    Figura\(\PageIndex{12}\)

    (De la Unidad 6.2.1)

    Ejercicio\(\PageIndex{8}\)

    Un cono tiene un volumen\(V\)\(r\), radio y una altura de 12 cm.

    1. Un cono tiene la misma altura y\(\frac{1}{3}\) del radio del cono original. Escribir una expresión para su volumen.
    2. Un cono tiene la misma altura y 3 veces el radio del cono original. Escribir una expresión para su volumen.

    (De la Unidad 5.5.2)

    This page titled 6.2.5: Observando más patrones en gráficas de dispersión is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.