8.2.1: Encontrar longitudes laterales de triángulos
- Page ID
- 118624
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Encontremos las longitudes de los lados del triángulo.
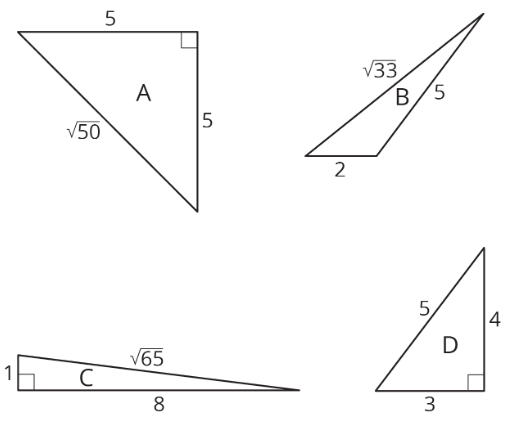
Ejercicio\(\PageIndex{1}\): Which One Doesn't Belong: Triangles
¿Qué triángulo no pertenece?
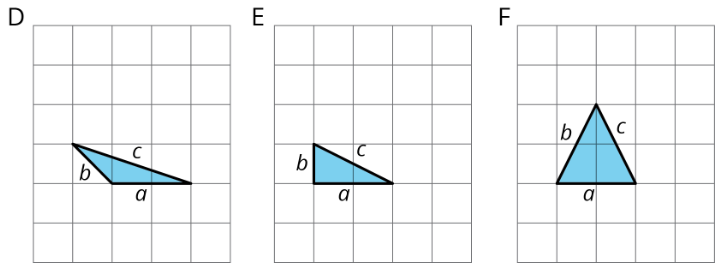
Ejercicio\(\PageIndex{2}\): A Table of Triangles
1. Completa las tablas para estos tres triángulos:
| triángulo | \(a\) | \(b\) | \(c\) |
|---|---|---|---|
| \(D\) | \ (a\) "> | \ (b\) "> | \ (c\) "> |
| \(E\) | \ (a\) "> | \ (b\) "> | \ (c\) "> |
| \(F\) | \ (a\) "> | \ (b\) "> | \ (c\) "> |
| triángulo | \(a^{2}\) | \(b^{2}\) | \(c^{2}\) |
|---|---|---|---|
| \(D\) | \ (a^ {2}\) "> | \ (b^ {2}\) "> | \ (c^ {2}\) "> |
| \(E\) | \ (a^ {2}\) "> | \ (b^ {2}\) "> | \ (c^ {2}\) "> |
| \(F\) | \ (a^ {2}\) "> | \ (b^ {2}\) "> | \ (c^ {2}\) "> |
2. ¿Qué nota acerca de los valores en la tabla para el Triángulo E pero no para los Triángulos D y F?
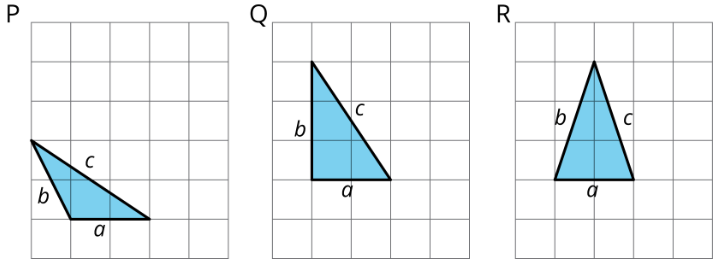
3. Completa las tablas para estos tres triángulos más:
| triángulo | \(a\) | \(b\) | \(c\) |
|---|---|---|---|
| \(P\) | \ (a\) "> | \ (b\) "> | \ (c\) "> |
| \(Q\) | \ (a\) "> | \ (b\) "> | \ (c\) "> |
| \(R\) | \ (a\) "> | \ (b\) "> | \ (c\) "> |
| triángulo | \(a^{2}\) | \(b^{2}\) | \(c^{2}\) |
|---|---|---|---|
| \(P\) | \ (a^ {2}\) "> | \ (b^ {2}\) "> | \ (c^ {2}\) "> |
| \(Q\) | \ (a^ {2}\) "> | \ (b^ {2}\) "> | \ (c^ {2}\) "> |
| \(R\) | \ (a^ {2}\) "> | \ (b^ {2}\) "> | \ (c^ {2}\) "> |
4. ¿Qué nota acerca de los valores en la tabla para Triángulo Q pero no para Triángulos P y R?
5. ¿Qué tienen en común el Triángulo E y el Triángulo Q?
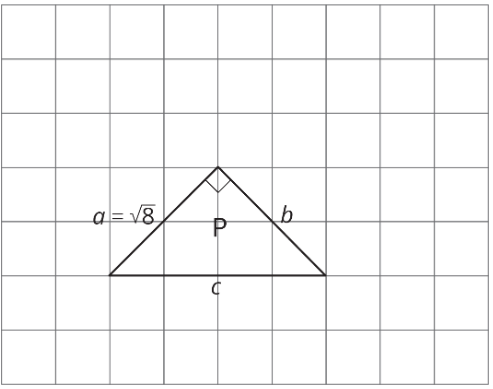
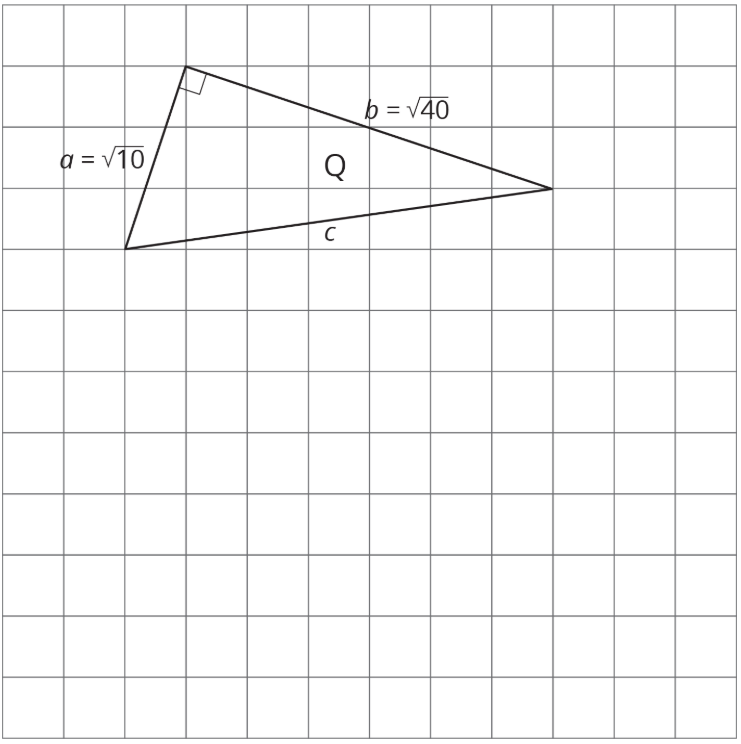
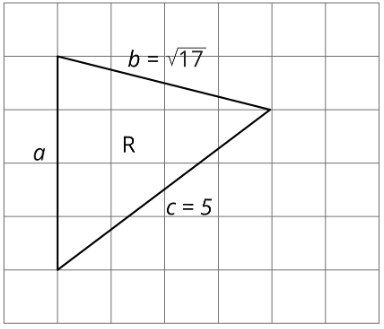
Ejercicio\(\PageIndex{3}\): Meet the Pythagorean Theorem
- Encuentra las longitudes laterales faltantes. Esté preparado para explicar su razonamiento.
- ¿Para qué triángulos hace\(a^{2}+b^{2}=c^{2}\)?
¿Estás listo para más?
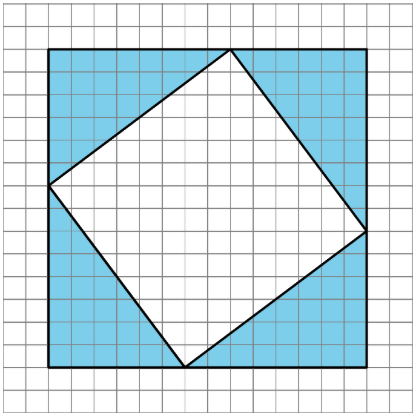
Si los cuatro triángulos sombreados en la figura son triángulos rectos congruentes, ¿el cuadrilátero interno tiene que ser un cuadrado? Explique cómo sabe.
Resumen
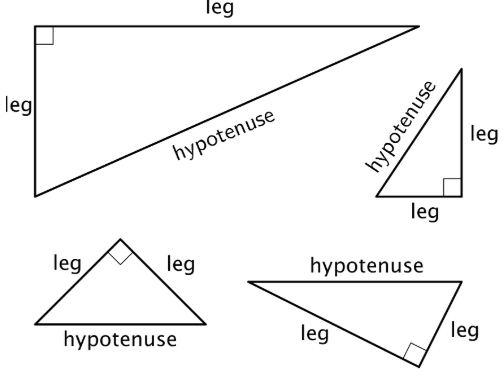
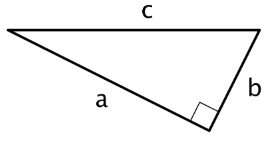
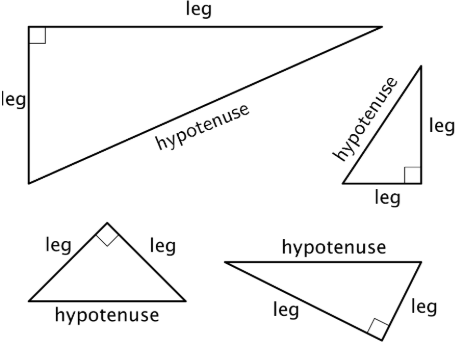
Un triángulo rectángulo es un triángulo con un ángulo recto. En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa, y los otros dos lados se llaman sus patas. Aquí hay algunos triángulos rectos con la hipotenusa y las piernas etiquetadas:
A menudo usamos las letras\(a\) y\(b\) para representar las longitudes de los lados más cortos de un triángulo y\(c\) para representar la longitud del lado más largo de un triángulo rectángulo. Si el triángulo es un triángulo rectángulo, entonces\(a\) y se\(b\) utilizan para representar las longitudes de las patas, y\(c\) se usa para representar la longitud de la hipotenusa (ya que la hipotenusa es siempre el lado más largo de un triángulo rectángulo). Por ejemplo, en este triángulo rectángulo,\(a=\sqrt{20}\),\(b=\sqrt{5}\), y\(c=5\).
Aquí hay algunos triángulos rectos:
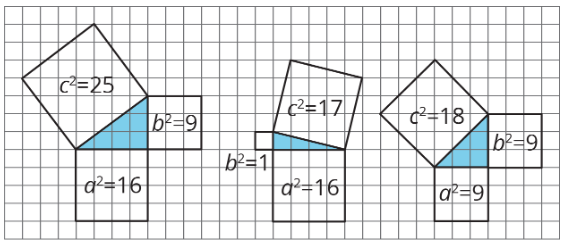
Observe que para estos ejemplos de triángulos rectos, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de las piernas. En el primer triángulo rectángulo en el diagrama,\(9+16=25\), en el segundo,\(1+16=17\), y en el tercero,\(9+9=18\). Expresado de otra manera, tenemos\(a^{2}+b^{2}=c^{2}\). Esta es una propiedad de todos los triángulos rectos, no solo de estos ejemplos, y a menudo se le conoce como el Teorema de Pitágoras. El nombre proviene de un matemático llamado Pitágoras que vivió en la antigua Grecia alrededor del 2.500 a. C., pero esta propiedad de los triángulos rectos también fue descubierta independientemente por matemáticos de otras culturas antiguas como Babilonia, India y China. En China, un nombre para la misma relación es el Teorema de Shang Gao. En lecciones futuras, aprenderás algunas formas de explicar por qué el Teorema de Pitágoras es cierto para cualquier triángulo rectángulo.
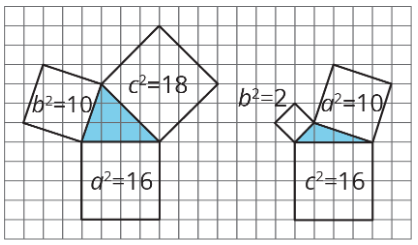
Es importante señalar que esta relación no se sostiene para todos los triángulos. Aquí algunos triángulos que no son triángulos rectos, y fíjense que las longitudes de sus lados no tienen la relación especial\(a^{2}+b^{2}=c^{2}\). Es decir,\(16+10\) no equivale a 18, y\(2+10\) no equivale a 16.
Entradas en el glosario
Definición: Teorema de Pitágoras
El Teorema de Pitágoras describe la relación entre las longitudes laterales de los triángulos rectos.
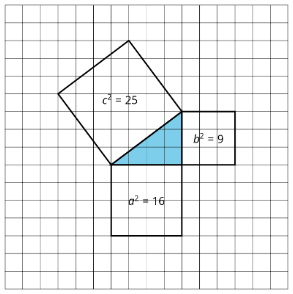
El diagrama muestra un triángulo rectángulo con cuadrados construidos a cada lado. Si agregamos las áreas de los dos cuadrados pequeños, obtenemos el área del cuadrado más grande.
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de las piernas. Esto está escrito como\(a^{2}+b^{2}=c^{2}\).
Definición: Hipotenusa
La hipotenusa es el lado de un triángulo rectángulo que está opuesto al ángulo recto. Es el lado más largo de un triángulo rectángulo.
Aquí hay algunos triángulos rectos. Cada hipotenusa está etiquetada.
Definición: LEGS
Las patas de un triángulo rectángulo son los lados que forman el ángulo recto.
Aquí hay algunos triángulos rectos. Cada pata está etiquetada.
Practica
Ejercicio\(\PageIndex{4}\)
Aquí hay un diagrama de un triángulo agudo y tres cuadrados.
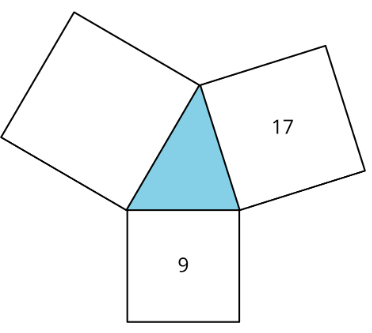
Priya dice que el área de la gran plaza sin marcar es de 26 unidades cuadradas porque\(9+17=26\). ¿Estás de acuerdo? Explica tu razonamiento.
Ejercicio\(\PageIndex{5}\)
\(m\),\(p\), y\(z\) representan las longitudes de los tres lados de este triángulo rectángulo.
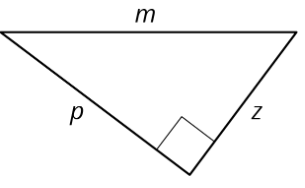
Seleccione todas las ecuaciones que representan la relación entre\(m\),\(p\), y\(z\).
- \(m^{2}+p^{2}=z^{2}\)
- \(m^{2}=p^{2}+z^{2}\)
- \(m^{2}=z^{2}+p^{2}\)
- \(p^{2}+m^{2}=z^{2}\)
- \(z^{2}+p^{2}=m^{2}\)
- \(p^{2}+z^{2}=m^{2}\)
Ejercicio\(\PageIndex{6}\)
Las longitudes de los tres lados se dan para varios triángulos rectos. Para cada uno, escriba una ecuación que exprese la relación entre las longitudes de los tres lados.
- \(10, 6, 8\)
- \(\sqrt{5}, \sqrt{3},\sqrt{8}\)
- \(5,\sqrt{5},\sqrt{30}\)
- \(1,\sqrt{37},6\)
- \(3,\sqrt{2},\sqrt{7}\)
Ejercicio\(\PageIndex{7}\)
Ordene las siguientes expresiones de menor a mayor.
\(25\div 10\qquad 250,000\div 1,000\qquad 2.5\div 1,000\qquad 0.025\div 1\)
(De la Unidad 4.1.1)
Ejercicio\(\PageIndex{8}\)
¿Cuál es la mejor explicación de por qué\(-\sqrt{10}\) es irracional?
- \(-\sqrt{10}\)es irracional porque no es racional.
- \(-\sqrt{10}\)es irracional porque es menor que cero.
- \(-\sqrt{10}\)es irracional porque no es un número entero.
- \(-\sqrt{10}\)es irracional porque si pongo\(-\sqrt{10}\) en un cálculo, me sale\(-3.16227766\), que no hace un patrón repetitivo.
(De la Unidad 8.1.3)
Ejercicio\(\PageIndex{9}\)
Una maestra les dice a sus alumnos que tiene poco más\(1\) y mil\(\frac{1}{2}\) millones de segundos de edad.
- Escribe su edad en segundos usando notación científica.
- ¿Cuál es una unidad de medida más razonable para esta situación?
- ¿Qué edad tiene cuando usas una unidad de medida más razonable?
(De la Unidad 7.3.7)