Saltar al contenido principal
LibreTexts Español

8.2.3: Encontrar longitudes de lado desconocidas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118639

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Encontremos las longitudes laterales faltantes de los triángulos rectos.

    Ejercicio\(\PageIndex{1}\): Which One Doesn't Belong: Equations

    ¿Cuál no pertenece?

    \(3^{2}+b^{2}=5^{2}\)

    \(b^{2}=5^{2}-3^{2}\)

    \(3^{2}+5^{2}=b^{2}\)

    \(3^{2}+4^{2}=5^{2}\)

    Ejercicio\(\PageIndex{2}\): Which One is the Hypotenuse?

    Etiquetar todas las hipotenusas con\(c\).

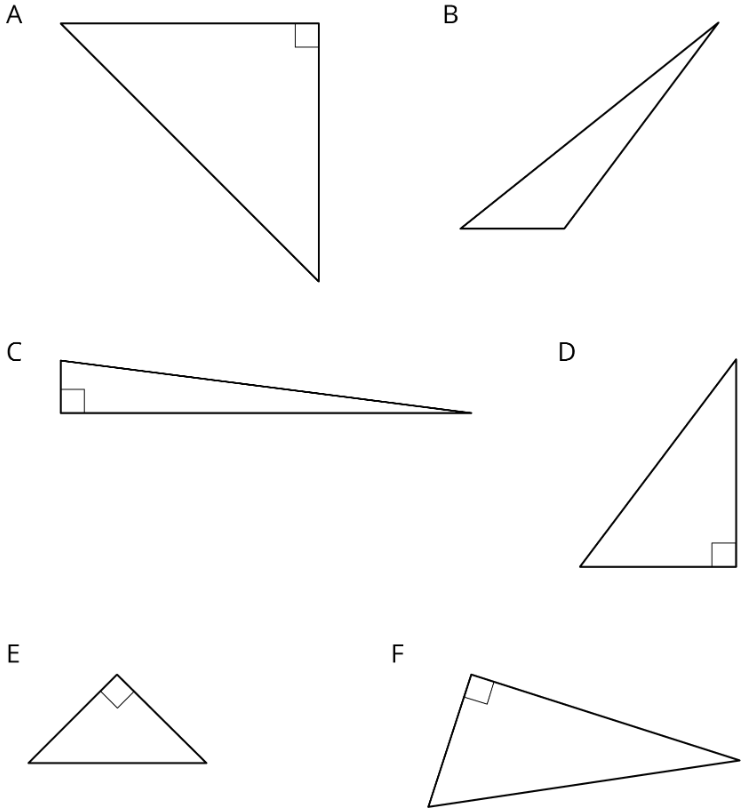
    clipboard_ea7e0959a09270f682e28e786e30b51dd.png
    Figura\(\PageIndex{1}\)

    Ejercicio\(\PageIndex{3}\): Find the Missing Side Lengths

    1. Encontrar\(c\).

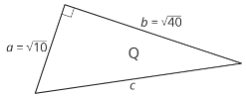
    clipboard_e4b175be2a59f62a1177cd573373fac01.png
    Figura\(\PageIndex{2}\)

    2. Encontrar\(b\).

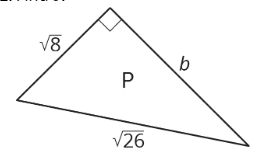
    clipboard_e73bc82d50b99587c618d7ae38bdf7e8d.png
    Figura\(\PageIndex{3}\)

    3. Un triángulo rectángulo tiene lados de longitud 2.4 cm y 6.5 cm. ¿Cuál es la longitud de la hipotenusa?

    4. Un triángulo rectángulo tiene un lado de longitud\(\frac{1}{4}\) y una hipotenusa de longitud\(\frac{1}{3}\). ¿Cuál es la longitud del otro lado?

    5. Encuentra el valor de\(x\) en la figura.

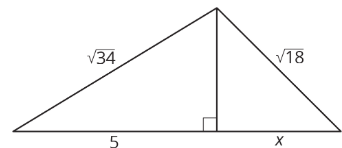
    clipboard_e934aa054383573febb22b387b98a21f2.png
    Figura\(\PageIndex{4}\)

    ¿Estás listo para más?

    La espiral en la figura se realiza comenzando con un triángulo rectángulo con ambas patas midiendo una unidad cada una. Después se construye un segundo triángulo rectángulo con una pata midiendo una unidad, y siendo la otra la hipotenusa del primer triángulo. Un tercer triángulo rectángulo se construye sobre la hipotenusa del segundo triángulo, nuevamente con la otra pierna midiendo una unidad, y así sucesivamente.

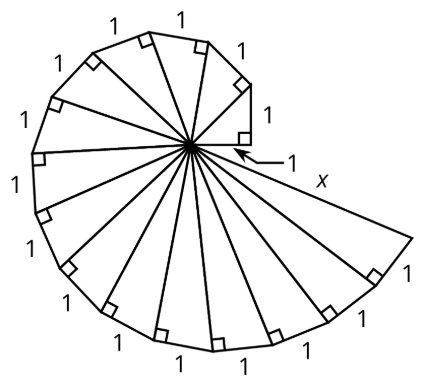
    clipboard_e24f0245967962b05d29b4c80314a892d.png
    Figura\(\PageIndex{5}\)

    Encuentra la longitud,\(x\), de la hipotenusa del último triángulo construido en la figura.

    Resumen

    Existen muchos ejemplos donde se conocen las longitudes de dos patas de un triángulo rectángulo y se pueden utilizar para encontrar la longitud de la hipotenusa con el Teorema de Pitágoras. El Teorema de Pitágoras también se puede utilizar si se conoce la longitud de la hipotenusa y una pierna, y queremos encontrar la longitud de la otra pierna. Aquí hay un triángulo rectángulo, donde una pata tiene una longitud de 5 unidades, la hipotenusa tiene una longitud de 10 unidades, y la longitud de la otra pierna está representada por\(g\).

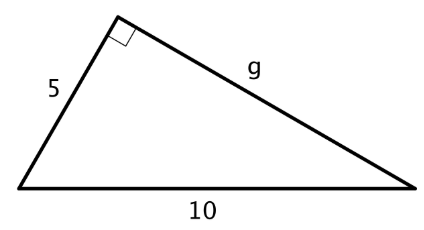
    clipboard_e114f8bb4e53e8b6e518d6dbe8749190d.png
    Figura\(\PageIndex{6}\)

    Comience con\(a^{2}+b^{2}=c^{2}\), haga sustituciones y resuelva el valor desconocido. Recuerda que\(c\) representa la hipotenusa: el lado opuesto al ángulo recto. Para este triángulo, la hipotenusa es 10.

    \[\begin{aligned} a^{2}+b^{2}&=c^{2}\\5^{2}+g^{2}&=10^{2}\\g^{2}&=10^{2}-5^{2}\\g^{2}&=100-25\\g^{2}&=75\\g&=\sqrt{25}\end{aligned}\nonumber\]

    Usa estrategias de estimación para saber que la longitud del otro tramo está entre 8 y 9 unidades, ya que 75 está entre 64 y 81. Una calculadora con una función de raíz cuadrada da\(\sqrt{75}\approx 8.66\).

    Entradas en el glosario

    Definición: Teorema de Pitágoras

    El Teorema de Pitágoras describe la relación entre las longitudes laterales de los triángulos rectos.

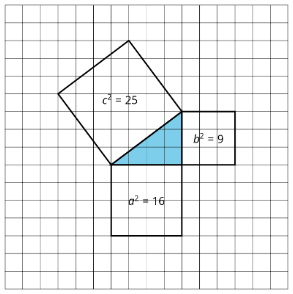
    El diagrama muestra un triángulo rectángulo con cuadrados construidos a cada lado. Si agregamos las áreas de los dos cuadrados pequeños, obtenemos el área del cuadrado más grande.

    El cuadrado de la hipotenusa es igual a la suma de los cuadrados de las piernas. Esto está escrito como\(a^{2}+b^{2}=c^{2}\).

    clipboard_e9b3f88fcfc66f9b4c409228918e38622.png
    Figura\(\PageIndex{7}\)

    Definición: Hipotenusa

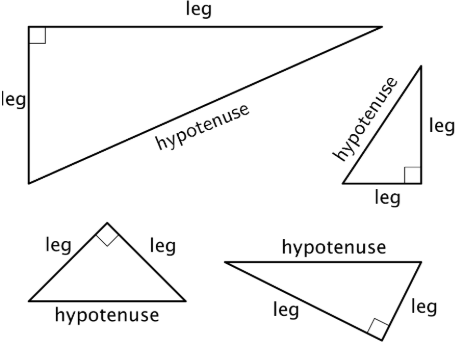
    La hipotenusa es el lado de un triángulo rectángulo que está opuesto al ángulo recto. Es el lado más largo de un triángulo rectángulo.

    Aquí hay algunos triángulos rectos. Cada hipotenusa está etiquetada.

    clipboard_ec6bc375731bd3956490eb84be58898f6.png
    Figura\(\PageIndex{8}\)

    Definición: LEGS

    Las patas de un triángulo rectángulo son los lados que forman el ángulo recto.

    Aquí hay algunos triángulos rectos. Cada pata está etiquetada.

    clipboard_ec6bc375731bd3956490eb84be58898f6.png
    Figura\(\PageIndex{9}\)

    Práctica

    Ejercicio\(\PageIndex{4}\)

    Encuentra el valor exacto de cada variable que representa una longitud lateral en un triángulo rectángulo.

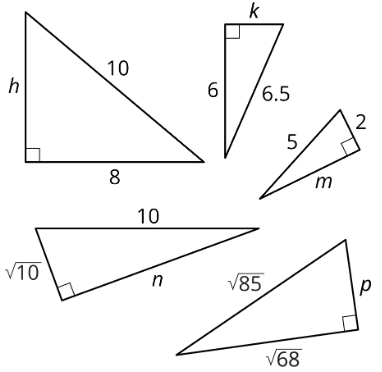
    clipboard_e5e8325dad1ada6f82d3c82b17a1a0864.png
    Figura\(\PageIndex{10}\)

    Ejercicio\(\PageIndex{5}\)

    Un triángulo rectángulo tiene longitudes laterales de\(a\)\(b\), y\(c\) unidades. El lado más largo tiene una longitud de\(c\) unidades. Complete cada ecuación para mostrar tres relaciones entre\(a\),\(b\), y\(c\).

    • \(c^{2}=\)
    • \(a^{2}=\)
    • \(b^{2}=\)

    (De la Unidad 8.2.2)

    Ejercicio\(\PageIndex{6}\)

    ¿Cuál es la longitud exacta de cada segmento de línea? Explica o muestra tu razonamiento. (Cada cuadrado de cuadrícula representa 1 unidad cuadrada).

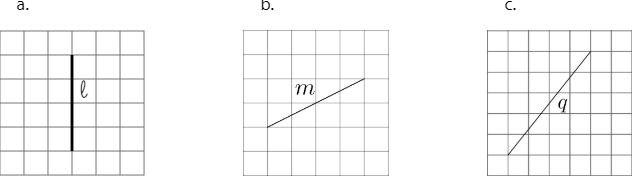
    clipboard_ec2502c7643c2063fca2c9eda07e3e7ba.png
    Figura\(\PageIndex{11}\)

    (De la Unidad 8.2.2)

    Ejercicio\(\PageIndex{7}\)

    En 2015, había aproximadamente jugadores de fútbol de\(1\times 10^{6}\) secundaria y futbolistas\(2\times 10^{3}\) profesionales en Estados Unidos. ¿Cuántas veces más futbolistas de secundaria hay? Explica cómo sabes.

    (De la Unidad 7.3.7)

    Ejercicio\(\PageIndex{8}\)

    Evaluar:

    1. \(\left(\frac{1}{2}\right)^{3}\)
    2. \(\left(\frac{1}{2}\right)^{-3}\)

    (De la Unidad 7.2.5)

    Ejercicio\(\PageIndex{9}\)

    Aquí hay un diagrama de dispersión de peso vs edad para diferentes dobermans. El modelo, representado por\(y=2.45x+1.22\), se grafica con el diagrama de dispersión. Aquí,\(x\) representa la edad en semanas, y representa el peso en libras.

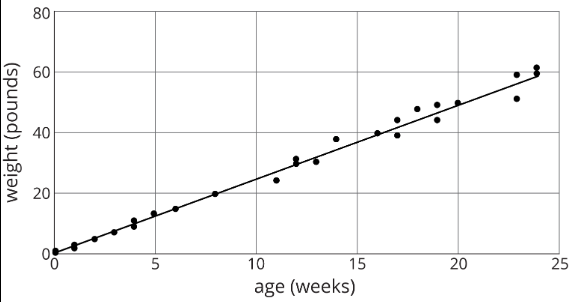
    clipboard_e0c025fb66720d458ddf7406fc6424112.png
    Figura\(\PageIndex{12}\)
    1. ¿Qué significa la pendiente en esta situación?
    2. Basado en este modelo, ¿qué tan pesado esperarías que fuera un Doberman recién nacido?

    (De la Unidad 6.2.4)

    This page titled 8.2.3: Encontrar longitudes de lado desconocidas is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.