5.4: Sumar y restar expresiones racionales

Última actualización
Guardar como PDF

Page ID: 115939

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Una fracción es una proporción. La fracción comunica el número de partes del conjunto.

$\dfrac{a}{b} \dfrac{\textcolor{blue}{\longleftarrow \text{The part is the numerator.}}}{\textcolor{blue}{\longleftarrow \text{The whole is the denominator.}}}$

Por ejemplo, la caja de huevos que se muestra a continuación contiene$10$ huevos. Parte de los huevos son marrones ($7$huevos) mientras que el resto son blancos ($3$huevos). Una fracción comunica$\dfrac{a}{b}$ rápidamente la proporción de huevos que son marrones o blancos. Las proporciones también se pueden dar como decimal o porcentaje.

$clipboard_e3c5408e1d01cd0704f558548ac275e13.png$

Proporción de huevos marrones:$\dfrac{7}{10} = 7 ÷ 10 = 0.7 = 70 \%$

Proporción de huevos blancos:$\dfrac{3}{10} = 3 ÷ 10 = 0.3 = 30 \%$

La proporción de huevos marrones y blancos describe todos los huevos. Intuitivamente, sabemos que esta proporción es$100 \%$. Las matemáticas deben coincidir con nuestra intuición, así que investiguemos.

$\begin{array} &70 \% + 30 \% &= 100 \% \\ \dfrac{7}{10} + \dfrac{3}{10} &= \dfrac{10}{10} \end{array}$

Nuestra investigación nos lleva a deducir que sumamos los numeradores, pero no los denominadores.

Para sumar o restar fracciones (el denominador es el mismo)

Sumar o restar los numeradores.
Mantener el mismo denominador.
Reducir si es necesario.

\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\]

Lo que funciona para números reales también funciona para cantidades algebraicas. El álgebra sigue las mismas reglas, lo cual es un excelente anclaje a partir del cual realizar sus propias investigaciones algebraicas.

Ejemplo 5.4.1

Agregar$\dfrac{2x}{x+3} + \dfrac{x}{x+3}$

Solución

Los denominadores coinciden. Agrega los dos numeradores, pero mantén el denominador.

$\dfrac{2x}{x+3} + \dfrac{x}{x+3} = \dfrac{2x+x}{x+3} = \dfrac{3x}{x+3}$

Como el resultado no se puede simplificar aún más, la respuesta es$\dfrac{3x}{x+3}$

Ejemplo 5.4.2

Restar$\dfrac{y^2+2y+8}{y^2−2y−15} − \dfrac{y^2+2}{y^2−2y−15}$

Solución

Los denominadores son los mismos. Restar los numeradores. Recuerda que cada numerador es una cantidad.

$\begin{array} &\dfrac{y^2+2y+8}{y^2−2y−15} − \dfrac{y^2+2}{y^2−2y−15} &= \dfrac{y^2+2y+8−(y^2+2)}{y^2−2y−15} &\text{Numerator: subtract the quantity \((y^2 + 2)$.}\\ & =\ dfrac {y^2+2y+8−y^2−2} {y^2−2y−15} &\ text {Se resta cada término de la cantidad.}\\ & =\ dfrac {2y+6} {y^2−2y−15} &\ text {La resta es completa.} \\ & =\ dfrac {2 (y+3)} {(y−5) (y+3)} &\ text {Numerador de factores y denominador. Cancelar.}\\ &=\ dfrac {2} {y−5} &\ text {La respuesta es más simplificada.} \ end {array}\)

Suma y resta con diferentes denominadores

Para sumar números racionales o expresiones racionales, necesitamos encontrar un denominador común. Crear denominadores comunes usando fracciones equivalentes. Es decir,$\dfrac{a \cdot \textcolor{red}{d}}{b \cdot \textcolor{red}{d}} = \dfrac{ad}{bd}$. Luego usa el proceso para sumar fracciones con denominadores comunes.

Ejemplo 5.4.3

Agregar$\dfrac{7}{75a^2b} + \dfrac{13}{180ab}$

Solución

Para encontrar el mínimo denominador común, jugamos un juego de “¿quién tiene más?” para cada denominador. Descomponer los denominadores en factores primos. Imagina que cada denominador es un conjunto de cartas, y cada carta es un factor del denominador. Porque tenemos dos denominadores, tenemos dos jugadores que jugarán el juego, “¿quién tiene más?”. Cualquiera que sea el jugador que tenga más de un factor “gana”, y coloca esas cartas en la pila ganadora. ¿Listo para jugar?

Jugador #$1$:$75a^2 \longrightarrow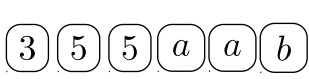$ $clipboard_e82900e65b6134c70d503b2fed4be7096.png$

Jugador #$2$:$180ab \longrightarrow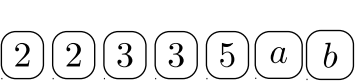$ $clipboard_ec69093ffe99e21d390dcc4c691e250bf.png$

¿Quién tiene más?	Jugador #$1$	Jugador #$2$	Pila ganadora
$2$'s		$\checkmark$	$2 \cdot 2$
$3$'s		$\checkmark$	$3 \cdot 3$
$5$'s	$\checkmark$		$5 \cdot 5$
$a$'s	$\checkmark$		$a \cdot a$
$b$'s	CORBATA	CORBATA	$b$

La pila ganadora$= 2^2 \cdot 3^2 \cdot 5^2 \cdot a^2 \cdot b$

El mínimo denominador común$= 900a^2b$

Usa el mínimo denominador común para crear un denominador común. Determinar qué factores faltan en cada denominador. Multiplique los factores faltantes al denominador y también al numerador. A continuación, agregue.

$\dfrac{7}{75a^2b} + \dfrac{13}{180ab} = \dfrac{7 \textcolor{red}{\cdot 12}}{75a^2b \textcolor{red}{\cdot 12}} + \dfrac{13 \textcolor{red}{\cdot 5a}}{180ab \textcolor{red}{\cdot 5a}} = \dfrac{84}{900a^2b} + \dfrac{65a}{900a^2b} = \dfrac{84+65a}{900a^2b} $.

La respuesta es:$\dfrac{84+65a}{900a^2b}$

Ejemplo 5.4.4

Agregar$\dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5}{(4y+1)(y+6)}$

Solución

En el juego de “¿quién tiene más?” las cantidades$(4y + 1)$ y$(y + 6)$ actuar como números únicos.

Jugador #$1$:$(4y + 1)^2 (y + 6) \longrightarrow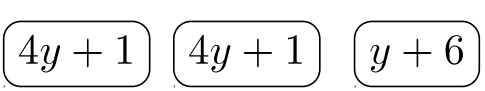$ $clipboard_ee200f708cfb0a13a36f0a1987aee86af.png$

Jugador #$2$:$(4y + 1)(y + 6) \longrightarrow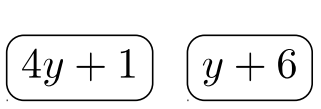$ $clipboard_e96fc9cb8c18dcb8c3ca506179e29e468.png$

Pila ganadora =$(4y + 1)^2 (y + 6)$ = Mínimo denominador común

$\begin{array} &\dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5}{(4y+1)(y+6)} &= \dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5 \textcolor{red}{\cdot (4y+1)}}{(4y+1)(y+6) \textcolor{red}{\cdot (4y+1)}} \\ &= \dfrac{2y+1+(20y+5)}{(4y+1)^2(y+6)} &\text{Simplify the numerator, but leave the denominator in factored form.} \\ &= \dfrac{22y+6}{(4y+1)^2(y+6)} &\text{The numerator is simplified. This is the answer!} \end{array}$

Consejo: El numerador se puede factorizar usando GCF$= 2$:$22y + 6 = 2(11y + 3)$. Sin embargo, esta factorización no conduce a una cancelación. Por lo tanto, se prefiere el numerador declarado.

Ejemplo 5.4.5

Restar$\dfrac{u^2+2u}{u^2+3u−10} − \dfrac{2u}{3u−6}$

Solución

Para comparar los factores de cada denominador, necesitamos factorizar.

$ \begin{array} &&\dfrac{u^2+2u}{u^2+3u−10} − \dfrac{2u}{3u−6} = \dfrac{u^2+2u}{(u+5)(u−2)} − \dfrac{2u}{3(u−2)} &\text{The denominators are factored.} \end{array}$

Juega el juego de “¿quién tiene más?” para encontrar el Mínimo Común Denominador. Las cantidades actúan como números únicos.

Jugador #$1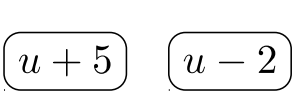$: $clipboard_e5b29d8142e8dc9709ca5f8f83c112282.png$

Jugador #$2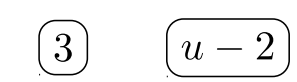$: $clipboard_e9db21ccf70da655263da0e7093153b56.png$

Denominador$= 3(u + 5)(u − 2) =$ mínimo común de pila ganadora

$\begin{array} &\dfrac{u^2+2u}{(u+5)(u−2)} − \dfrac{2u}{3(u−2)} &= \dfrac{\textcolor{red}{3}(u^2+2u)}{\textcolor{red}{3}(u+5)(u−2)} − \dfrac{2u \textcolor{red}{(u+5)}}{3(u−2) \textcolor{red}{(u+5)}} &\text{Determine the missing factors & multiply.} \\ &= \dfrac{3u^2+6u}{3(u+5)(u−2)} − \dfrac{2u^2+10u}{3(u+5)(u−2)} &\text{Simplify numerators.} \\ &= \dfrac{3u^2+6u−(2u^2+10u)}{3(u+5)(u−2)} &\text{Numerator: subtract the quantity.} \\ &= \dfrac{3u^2+6u−2u^2−10u}{3(u+5)(u−2)} &\text{Subtract each term of the quantity.} \\ &= \dfrac{u^2−4u}{3(u+5)(u−2)} &\text{The numerator is simplified. This is the answer!} \end{array}$

Consejo: El numerador se puede factorizar usando GCF$= u$:$u^2 − 4u = u(u − 4)$. Sin embargo, esta factorización no conduce a una cancelación. Por lo tanto, se prefiere el numerador declarado.

Ejemplo 5.4.6

Restar$\dfrac{3c}{49−c^2} − \dfrac{1}{c^2−7c}$

Solución

Para comparar los factores de cada denominador, necesitamos factorizar.

$\begin{array} &&\dfrac{3c}{(7−c)(7+c)} − \dfrac{1}{c(c−7)} &\text{The denominators are factored.} \end{array}$

Juega el juego de “¿quién tiene más?” para encontrar el Mínimo Común Denominador. Las cantidades actúan como números únicos.

Jugador #$1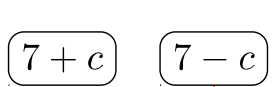$: $clipboard_e536c760e466e1d3499db5678220afecb.png$

Jugador #$2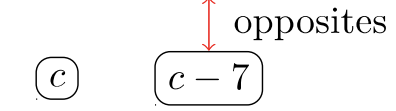$: $clipboard_e078fec96a07e13d83128820663fd76ea.png$

Nota:$7 − c$ y$c − 7$ son opuestos. Al ser opuestos, se puede hacer que una cantidad se “parezca” a la otra.

$7 − c = −(c − 7)$

A continuación, rebotar el negativo al numerador. ¡Voilà! Así es como hacemos un Mínimo Común Denominador.

Denominador$= c(c + 7)(c − 7) =$ mínimo común de pila ganadora

$\begin{array} &\dfrac{3c}{(7−c)(7+c)} − \dfrac{1}{c(c−7)} &= \dfrac{3c}{\textcolor{red}{−}(c−7)(7+c)} −\dfrac{1}{c(c−7)} &\text{Replace \(7 − c$con$−(c − 7)$.} \\ & =\ dfrac {\ textcolor {red} {−} 3c} {(c−7) (7+c)} −\ dfrac {1} {c (c−7)} &\ text {Desde$\dfrac{a}{−b} = \dfrac{-a}{b}$, pon el negativo en la parte superior.}\\ & =\ dfrac {−3c\ cdot\ textcolor {rojo} {c}} {\ textcolor {rojo} c {} (c−7) (c+7)} −\ dfrac {1\ textcolor {rojo} {\ cdot (c+7)}} {c (c−7)\ textcolor {rojo} {(c+7)}} &\ text {Construye la pantalla LCD. Nota:$7 + c = c + 7$.}\\ & =\ dfrac {−3c^2− (c+7)} {c (c−7) (c+7)} &\ text {Numerador: restar la cantidad.}\\ &=\ dfrac {−3c^2−c−7} {c (c−7) (c+7)} &\ text {El numerador ha sido simplificado.}\\ &=\ dfrac {− 3c^2+c+7} {c (c−7) (c+7)} &\ text {Factor de salida$−1$.} \ end {array}\)

Cualquiera de las dos últimas líneas podría ser tu respuesta final. ¿Cuál prefieres? ¡Es tu elección!

Nota

Después de simplificar el numerador, haz una pausa y pregúntate: “¿qué más puedo hacer para simplificar?” Si el numerador es factorizable, comprueba si los factores son los mismos que los del denominador. Si es así, cancele los factores comunes. Mantén el denominador factorizado para recordarte a ti mismo (y a tu lector) qué factores no cancelan.

¡Pruébalo! (Ejercicios)

Para #1 -20, sumar o restar las expresiones racionales como se indica.

$\dfrac{5x}{3y^2} + \dfrac{x}{3y^2}$
$\dfrac{14a}{5b} − \dfrac{4a}{5b}$
$\dfrac{4r}{9qp} + \dfrac{1}{3q^2p}$
$\dfrac{1−n}{6n} + \dfrac{2n+1}{3n}$
$\dfrac{n+2}{12m^3} − \dfrac{2}{3m^3n}$
$\dfrac{t+6}{t+5} + \dfrac{t+4}{t+5}$
$\dfrac{6c+1}{(5c+2)^3} − \dfrac{c−1}{(5c+2)^3}$
$\dfrac{2}{x−3} + \dfrac{3}{10}$
$\dfrac{4}{y+2} + \dfrac{2}{3y+6}$
$\dfrac{3}{x+3} − \dfrac{3}{x−3}$
$\dfrac{h−2}{(h+1)^2} + \dfrac{2}{3h+3}$
$\dfrac{5}{y−1} − \dfrac{3}{y^2−1}$
$\dfrac{−2}{a^2−5a+6} + \dfrac{2}{a−3}$
$\dfrac{4}{d−3} − \dfrac{5d−12}{d^2−6d+9}$
$\dfrac{5}{v^2−5v} − \dfrac{v}{5v−25}$
$\dfrac{1−n}{n^2−4} − \dfrac{n−2}{n^2−2n−8}$
$3 + \dfrac{x}{ x+2}$
$\dfrac{3p−1}{p^2+5p+6} + \dfrac{2p−3}{p^2+3p+2}$
$\dfrac{3}{q+3} + \dfrac{2q}{q^2+8q+15}$
$\dfrac{w+2}{4w+16} − \dfrac{2}{w^2+4w}$

Para #21 -30, ocurren cantidades opuestas. Sumar o restar las expresiones racionales como se indica.

$\dfrac{3}{8} + \dfrac{5}{−8}$
$\dfrac{y^2}{y−5} + \dfrac{4y+5}{5−y}$
$\dfrac{6}{w−2} + \dfrac{w+3}{2−w}$
$\dfrac{2a−7}{5a−8} + \dfrac{6+10a}{8−5a}$
$\dfrac{u^2−2}{2u^2−u−3} + \dfrac{u−2}{3−2u}$
$\dfrac{b−23}{b^2−b −20} − \dfrac{2}{5−b}$
$\dfrac{t+1}{t−1} − \dfrac{3t^2−1}{1−t^2}$
$\dfrac{2}{6−3x} + \dfrac{x}{x^2−4}$
$\dfrac{5r}{1−2r} − \dfrac{2r}{2r+1} + \dfrac{3}{4r^2−1}$
$\dfrac{2y}{y^2−9} − 1 + \dfrac{4}{3−y}$

¿Quién tiene más?	Jugador #\(1\)	Jugador #\(2\)	Pila ganadora
\(2\)'s		\(\checkmark\)	\(2 \cdot 2\)
\(3\)'s		\(\checkmark\)	\(3 \cdot 3\)
\(5\)'s	\(\checkmark\)		\(5 \cdot 5\)
\(a\)'s	\(\checkmark\)		\(a \cdot a\)
\(b\)'s	CORBATA	CORBATA	\(b\)