6.2: Sumar y restar expresiones radicales

Última actualización
Guardar como PDF

Page ID: 115864

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Las reglas para la multiplicación y división radicales tienen una simplicidad y facilidad que arrulla a los estudiantes para que piensen que la suma y la resta seguirán su ejemplo. Sin embargo, las reglas de suma y resta tienen más complicaciones y menos flexibilidad. Empecemos con el escollo más común:

$\sqrt[n]{a} + \sqrt[n]{b} \neq \sqrt[n]{a+b}$

Nota: El símbolo$\neq$ dice “no es igual”.

Estos dos ejemplos tienen aún más tentación de equivocarse debido a la cuadratura y las variables:

$\sqrt{x^2 + y^2} \neq x+y$

También,

$\sqrt{x^2 - y^2} \neq x-y$

¡Esto no cambia ninguna propiedad que se introdujo anteriormente! ¡Lo siguiente sigue siendo cierto! ($x ≥ 0$y$y ≥ 0$ si$n$ es par)

$\sqrt{x^2} + \sqrt{y^2} = x + y$

$\sqrt{x^2} - \sqrt{y^2} = x - y$

Y en general,

$\sqrt[n]{x^n} + \sqrt[n]{y^n} = x ± y$

Usa una calculadora para convencerte a ti mismo:

$\sqrt{6} + \sqrt{2} \neq \sqrt{8}$

En el lado izquierdo, encuentra el valor$\sqrt{6} + \sqrt{2}$ a la centésima más cercana:

$\sqrt{6} + \sqrt{2} ≈ 3.86$

En el lado derecho,

$\sqrt{8} ≈ 2.83$

Ahora vemos que no se pueden agregar radicandos:

$3.86 \neq 2.83$

Utilizar el orden de las operaciones a medida que se presenta el problema. Cualquier otro orden de cálculo podría ser un escollo.

$\textcolor{green}{\checkmark} \sqrt[3]{27} + \sqrt[3]{8} = 3+ 2 =5 $

El orden de las operaciones nos dice que primero tomemos la raíz cube y luego agreguemos. ¡Usa el pedido que se muestra y será correcto!

Uso de “Términos Me gusta” para agregar o restar “como radicandos”

Agregar y restar radicales comienza con la simplificación de radicales. Utilice con la mayor frecuencia posible la propiedad$\sqrt[n]{a^n} = a$ para simplificar los radicales. Continuaremos asumiendo que las variables solo toman valores no negativos. Exploremos cómo reunir términos similares se pueden usar con radicales.

$2x + x = 3x$$x =$cualquier número real

Reunir términos similares es una técnica que has usado innumerables veces antes. ¿Por qué no usar con radicales? ¡Los radicales también son números reales! Este enfoque abre nuestra caja de herramientas para sumar o restar expresiones radicales. Podemos agregar radicales si el radicando es idéntico y el índice$n$ también coincide.

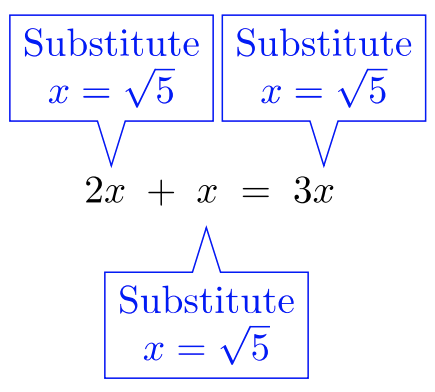
$clipboard_e5b839b7d59c7487ff6af0c292561f2da.png$

Supongamos$x = \sqrt{5}$. Reúne como radicales:

$2\sqrt{5} + \sqrt{5} = 3\sqrt{5}$

Definición: Like Radicals

Se dice que dos términos radicales son como radicales si tienen el mismo índice y el mismo radicando.

Ejemplo 6.2.1

¿Cuál de las tres expresiones se puede simplificar? Explique.

$4 \sqrt[3]{10} + 7 \sqrt[3]{10}$
$3 \sqrt{2} + 3 \sqrt{11}$
$\sqrt[3]{6} + \sqrt{6}$

Solución

Esta es la única expresión dada de las tres que se pueden simplificar.

$4 \sqrt[3]{10} + 7 \sqrt[3]{10} = 11\sqrt[3]{10}$

$4 \sqrt[3]{10} \text{ and } 7 \sqrt[3]{10}$ambos contienen$\sqrt[3]{10}$ como radicales similares.

No se puede simplificar.

$3 \sqrt{2} \neq 3 \sqrt{11}$

Los radicandos no son iguales.

No se puede simplificar.

$\sqrt[3]{6} \neq \sqrt{6}$

Los índices no son iguales.

Simplifique primero

¿No ves un partido? Asegúrate de que tus radicales estén completamente simplificados antes de intentar sumar o restar radicales. Los siguientes ejemplos demuestran cómo la simplificación puede ayudarte a encontrar radicales similares.

Ejemplo 6.2.2

Simplificar$\sqrt{75} + 2 \sqrt{12} − \sqrt{3}$

Solución

$\begin{array} &\sqrt{75} + 2 \sqrt{12} − 5 \sqrt{3}& &\text{At first glance, none of the radicals are like radicals. However, both \(\sqrt{75}$y se$\sqrt{12}$ puede simplificar.}\\ & =\ sqrt {25\ cdot 3} + 2\ sqrt {4\ cdot 3} −\ sqrt {3} &\ text {Factor cuadrados perfectos dentro de cada radicando.}\\ &= 5\ sqrt {3} + 2\ cdot 2\ sqrt {3} −\ sqrt {3} &\ text {Simplificar.}\\ &= 5\ sqrt {3} + 4\ sqrt {3} −\ sqrt {3} &\ text {Combina como radicales.}\\ (5 + 4 − 1)\ sqrt {3} &= 8\ sqrt {3} &\ end {array}\)

Ejemplo 6.2.3

Agregar$\sqrt[3]{54x^2} + \sqrt[3]{3x^2} + \sqrt[3]{16x^2}$

Solución

$\begin{array} &&\sqrt[3]{54x^2} + \sqrt[3]{3x^2} + \sqrt[3]{16x^2} &\text{Simplify each radical.} \\ &= \sqrt[3]{27 \cdot 2x^2} + \sqrt[3]{3x^2} + \sqrt[3]{8 \cdot 2x^2} &\text{Factor the radicands.} \\ &= 3 \textcolor{red}{\sqrt[3]{2x^2}} + \sqrt[3]{3x^2} + 2 \textcolor{red}{\sqrt[3]{3x^2}} &\text{Two terms contain like radicals. Simplify. } \\ &= 5 \sqrt[3]{3x^2} + \sqrt[3]{3x^2} & \end{array}$

Ejemplo 6.2.4

Encuentra el área y el perímetro del rectángulo mostrado.

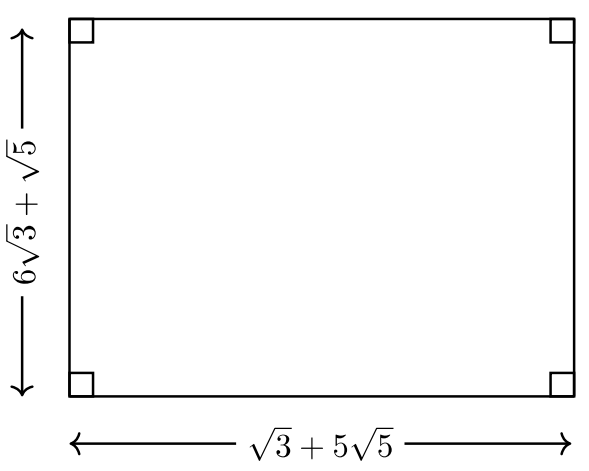
$clipboard_e9e5cd0bd0869ddef6196db5a9138cd68.png$

Longitud$= (6 \sqrt{3} + \sqrt{5})$ pies

$= (\sqrt{3} + 5\sqrt{5})$Pies de ancho

Solución

Utilice FOIL:

$\begin{array} &&\text{Area } &= (6 \sqrt{3} + \sqrt{5})(\sqrt{3} + 5\sqrt{5}) &= \underbrace{(6 \sqrt{3})(\sqrt{3})}_{\text{F}} + \underbrace{(6 \sqrt{3})(5\sqrt{5})}_{\text{O}} + \underbrace{(\sqrt{5})(\sqrt{3})}_{\text{I}} + \underbrace{(\sqrt{5})(5\sqrt{5})}_{\text{L}} \\ &&&= 6 \cdot 3 + 6 \cdot 5 \cdot \sqrt{3 \cdot 5} + \sqrt{5 \cdot 3} + 5 \cdot 5 \\&&&= 18 + 30\sqrt{15} + \sqrt{15} +25 \\&&&= 43 +31\sqrt{15} \text{ ft}^2 \end{array}$

$\begin{array} &&\text{Perimeter } &= \overbrace{2(6 \sqrt{3} + \sqrt{5}) + 2(\sqrt{3} + 5\sqrt{5})}^{P = 2L + 2W} &= \underbrace{(2 \cdot 6 \sqrt{3} + 2 \cdot \sqrt{5})}_{\text{Distributive Property}} + \underbrace{(2 \cdot \sqrt{3} + 2 \cdot 5\sqrt{5})}_{\text{Distributive Property}} \\ &&&= (12 \sqrt{3} + 2 \sqrt{5}) + (2 \sqrt{3} + 2 \cdot 5\sqrt{5}) \\&&&= \underbrace{12 \sqrt{3} + 2\sqrt{3}}_{\text{Like Radicals}} + \underbrace{2\sqrt{5}+10\sqrt{5}}_{\text{Like Radicals}} \\&&&= 14\sqrt{3} + 12\sqrt{5} \text{ ft}^2 \end{array}$

¡Pruébalo! (Ejercicios)

Para #1 -4, suma o resta las expresiones, si es posible. Supongamos que las variables representan números no negativos.

$7\sqrt{5} − 2\sqrt{5} + \sqrt{5}$
$3\sqrt{3x} − 4\sqrt{3x} + 6\sqrt{6x} − 8\sqrt{6x}$
$\sqrt[3]{9y} + \sqrt[4]{9y} − \sqrt[3]{2y} + 2\sqrt[4]{9y}$
$7b \sqrt[5]{16b^2} − 4b\sqrt[3]{16b^2} − 3b\sqrt[5]{3b^2}$

Para #5 -8, simplifica cada expresión radical, luego suma o resta las expresiones, si es posible. Supongamos que las variables representan números no negativos.

$2\sqrt{3a^3} + 5a\sqrt{3a} − \sqrt{27a^3}$
$\sqrt[3]{56c^6} − 2c^2 \cdot \sqrt[3]{189} + \sqrt[3]{7c^2} $
$3\sqrt[4]{4p^7} − 3p\sqrt[4]{324p^3} + 2\sqrt[4]{64p^7}$
$2b\sqrt[5]{192b^3} − \sqrt[5]{64b} + 3\sqrt[5]{6b^8} + \sqrt[5]{486b}$

Para #9 -14, evalúe cada uno de los siguientes. Simplifique siempre que sea posible. Supongamos que las variables representan números no negativos.

$\sqrt{12}(\sqrt{2} − \sqrt{18})$
$(7\sqrt[3]{10} + 3\sqrt[3]{4})(2\sqrt[3]{20} − \sqrt[3]{50})$
$(9\sqrt{2x} + 6\sqrt{3x})^2$
$(\sqrt{26} − 4\sqrt{10})(\sqrt{26} + 4\sqrt{10})$
$(\sqrt[3]{24} − \sqrt[3]{54})^2$
$5(3\sqrt{7} − 1)(4\sqrt{14} + 1)$

Para #15 -16, encuentra el área y el perímetro de cada rectángulo. El largo y ancho están marcados cada uno en las figuras y las unidades son pies.

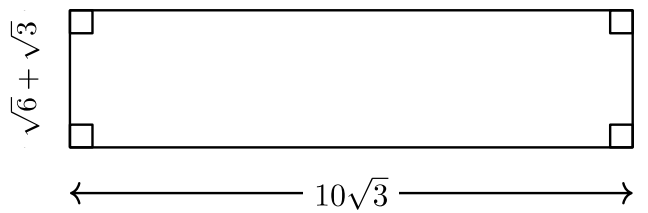
$clipboard_ee3bb371de39b456d6c73cfeeb3def10f.png$
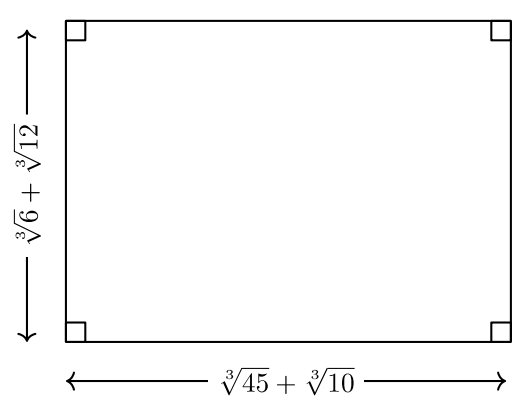
$clipboard_e2ae9bd4a09dde96bb8e3712b6624465a.png$
Un cuadrado tiene longitudes laterales =$(\sqrt[4]{4} + 2)$ pies. Encuentra cada una de la zona y el perímetro de la plaza.
Si un cuadrado tiene área$= 540$$\text{ft}^2$. ¿Cuál es el perímetro de la plaza?