Saltar al contenido principal
LibreTexts Español

7.1: El Círculo de Unidades

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    115813

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

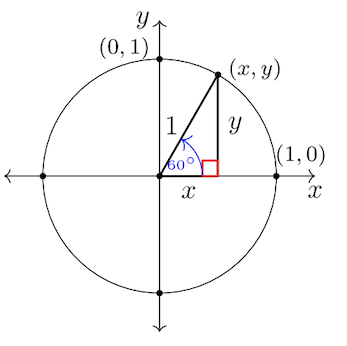
    Los conceptos centrales de la trigonometría se desarrollan a partir de un círculo con radio igual a la\(1\) unidad, dibujado en el plano\(xy\) -coordenado, centrado en el origen. A este círculo se le da un nombre: el círculo unitario (Figura\(7.1.1\) abajo). Al igual que un reloj\(12\) de hora con valores de tiempo desde\(1\) hasta\(12\), las funciones trigonométricas son periódicas, es decir, los mismos valores se reproducen con cada\(360˚\) revolución.

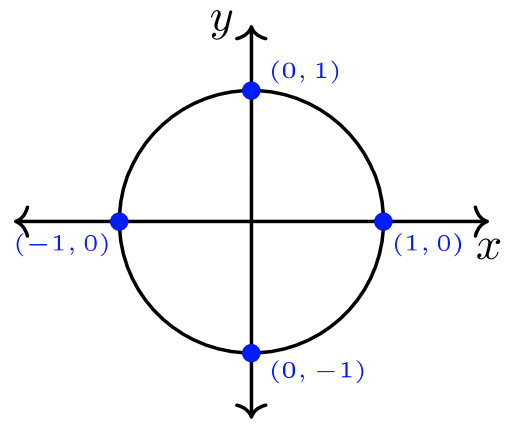
    clipboard_ee9194d291a410069f87c8e1e3c3c96ce.png
    Figura 7.1.1 : El círculo de unidades
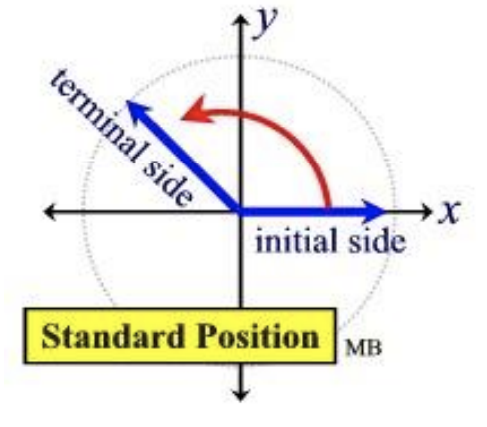
    clipboard_ea5f43bf8eda27a54721c85d7bedd2294.png
    Figura 7.1.2 : Ángulos en posición estándar

    Un ángulo está en posición estándar (ver Figura\(7.1.2\) anterior) si su lado inicial está a lo largo del\(x\) eje positivo y su vértice está en el origen: punto\((0,0)\). Los siguientes ángulos están en posición estándar. Un ángulo que gira en sentido contrario a las agujas del reloj es un ángulo positivo. Un ángulo que gira en el sentido de las agujas del reloj es un ángulo negativo.

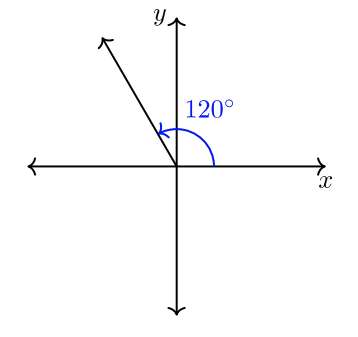
    clipboard_e5a9241cdbae64a1f379bb2913b24dca3.png
    Figura 7.1.3 : Ángulo positivo en posición estándar.
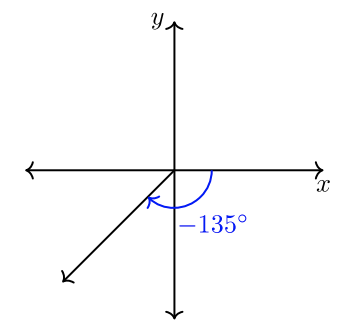
    clipboard_eb1748bdb896646cba2fe3b8eb41231d6.png
    Figura 7.1.4 :: Ángulo negativo en posición estándar.
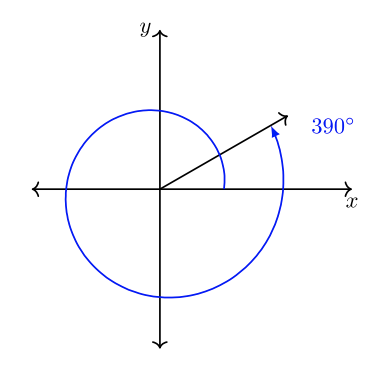
    clipboard_ef1b42094cc065a1ffc226a4b8dfee163.png
    Figura 7.1.5 : Ángulo positivo en posición estándar.

    Ángulos coterminales

    Se dice que dos o más ángulos estándar que comparten lados terminales comunes son ángulos coterminales. Por ejemplo,\(30˚\) y\(390˚\) son ángulos coterminales.

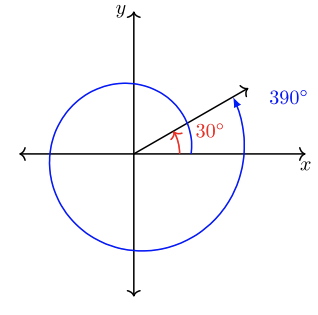
    clipboard_edae1eab80f059ab6160333bcf21dad75.png

    Más formalmente: Cada ángulo\(B\) es coterminal con ángulo\(A\) donde\(B = A + 360˚k\),\(k =\) cualquier entero.

    Ejemplo 7.1.1

    La expresión\(315˚ + 360˚k\) da los ángulos coterminales con\(315˚\). Indique los ángulos coterminales que genera la ecuación utilizando los siguientes\(k\) -valores:\(k = −2, −1, 1, 2\). Después bosquejar los ángulos.

    Solución

    Sustituimos los\(k\) valores dados en la expresión\(315˚ + 360˚k\).

    \(k = -2\) \(k = -1\) \(k = 1\) \(k = 2\)
    \(315˚ + 360˚(\textcolor{red}{-2}) = -405˚\) \(315˚ + 360˚(\textcolor{red}{-1}) = -45˚\) \(315˚ + 360˚(\textcolor{red}{1}) = -675˚\) \(315˚ + 360˚(\textcolor{red}{2}) = 1035˚\)

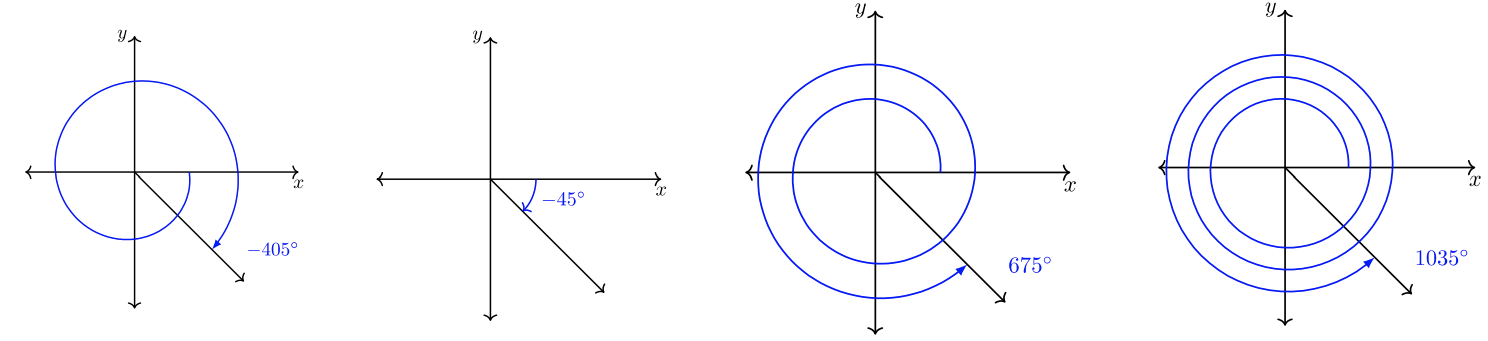
    Abajo, se esbozan los ángulos. ¿Ves que cada ángulo comparte el mismo lado terminal? Los cuatro ángulos son coterminales y coterminales entre sí.\(315˚\)

    clipboard_e817c28fbb916447571993b1ba5b92c18.png

    Círculo Centrado en el Origen

    Cada par ordenado\((x, y)\) en un círculo está asociado con un triángulo rectángulo. El triángulo rectángulo tiene distancia horizontal\(x\)\(y\), distancia vertical e hipotenusa = radio =\(r\).

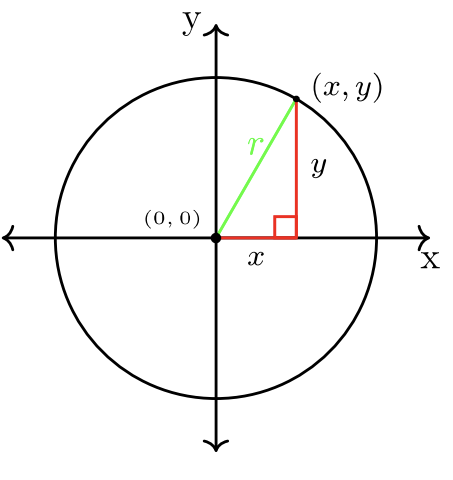
    clipboard_ea4f396a40a55f4929eb6dd6b1ad1cbda.png

    Ecuación de un círculo

    La ecuación de un círculo de radio\(r\) centrado en el origen:

    \[x^2 + y^2 = r^2\]

    Nota: la\(x\) coordenada\(y\) -y la coordenada -pueden tomar valores negativos, dependiendo del cuadrante del lado terminal del ángulo.

    Ejemplo 7.1.2

    Encuentre la\(y\) coordenada -del punto A\(\left(−\dfrac{5}{9} , y \right)\) si el punto A se encuentra en QIII en el círculo unitario.

    Solución

    El círculo unitario tiene radio\(r = 1\). La trigonometría conecta álgebra y geometría con bocetos visuales. Crea un boceto antes de saltar a una solución. Esto te ayuda a ver la respuesta.

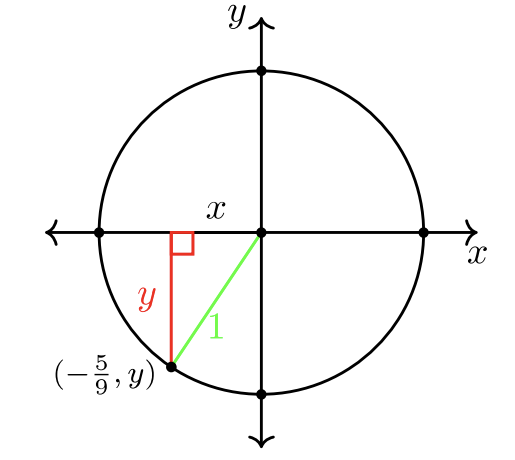
    clipboard_ed6aa5e0ff457f2cdadcf335269d53625.png

    \(\begin{array} &\left(−\dfrac{5}{9}\right)^2 + y^2 &= 1^2 &\text{Substitute \(x = −\dfrac{5}{9}\)y\(r = 1\) en la ecuación de un círculo.}\\\ dfrac {25} {81} + y^2 &= 1 &\ text {Simplificar.}\\ y^2 &= 1 −\ dfrac {25} {81} &\ text {Restar\(\dfrac{25}{81}\) a cada lado.}\\ y^2 &=\ dfrac {81} {81} −\ dfrac {25} {81} &\ text {Encuentra la pantalla LCD.}\\ y^2 &=\ dfrac {56} {81} &\ text {Simplificar.} \\ sqrt {y^2} &= ±\ sqrt {\ dfrac {56} {81}} &\ text {Raíz cuadrada de ambos lados.}\\ y &= −\ dfrac {\ sqrt {56}} {9} &\ text {Elige el valor de signo correcto. \(y < 0\)en QIII.}\\ y &= −\ dfrac {2\ sqrt {14}} {9} &\ text {Simplifica el radical.} \ end {array}\)

    Triángulos Retos Especiales

    Usando el Teorema de Pitágoras, se pueden manejar las siguientes dos plantillas para triángulos rectos especiales:\(45˚\)\(45˚\) - -\(90˚\) triángulos y\(30˚\) -\(60˚\) -\(90˚\) triángulos.

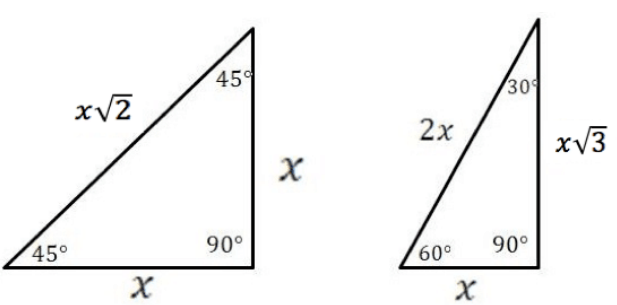
    clipboard_e2026a8b9c765a82686d89e448e76dfa7.png

    Dado que los triángulos rectos y los círculos están inextricablemente ligados entre sí\(30˚\), los ángulos agudos\(45˚\),\(60˚\) suelen ser útiles para encontrar valores exactos en trigonometría; estas soluciones no requieren el uso de una calculadora.

    Ejemplos de triángulos rectos especiales y sus soluciones, se pueden ver en estos videos:

    ¡Pruébalo! (Ejercicios)

    Para #1 -5, dibuje el ángulo\(\theta\) en posición estándar.

    1. \(\theta = 210˚\)
    2. \(\theta = −300˚\)
    3. \(\theta = 150˚\)
    4. \(\theta = 270˚\)
    5. \(\theta = −135˚\)

    Para #6 -10, indica cualquiera de los dos ángulos coterminales con el ángulo dado\(\theta\). Dar un ángulo coterminal positivo y un ángulo coterminal negativo.

    1. \(\theta = 30˚\)
    2. \(\theta = 60˚\)
    3. \(\theta = 90˚\)
    4. \(\theta = 180˚\)
    5. \(\theta = 240˚\)

    Para #11 -15, indica la ecuación del círculo con el radio dado.

    1. \(r = 4\)
    2. \(r = \dfrac{1}{2}\)
    3. \(r = 3 \sqrt{2}\)
    4. \(r = \dfrac{\sqrt{6}}{2}\)
    5. \(r = \sqrt{\dfrac{101}{62}}\)
    6. Rellene los espacios en blanco: Un círculo unitario es un círculo con\(\underline{\;\;\;\;\;\;\;\;\;\;}\) igual a una unidad. El círculo está centrado en\(\underline{\;\;\;\;\;\;\;\;\;\;}\). El círculo tiene ecuación:\(\underline{\;\;\;\;\;\;\;\;\;\;}\).

    Para #17 -24, El punto dado se encuentra en un círculo con radio dado y lado terminal en el cuadrante dado. Encuentra la coordenada faltante del par ordenado dado.

    Punto en círculo Radio Cuadrante en el que\(\theta\) termina.
    17. \((2, y)\) \(r = 5\) \ (\ theta\) termina.” >\(\theta ∈\) QI
    18. \((x, \sqrt{6})\) \(r = 3\) \ (\ theta\) termina.” >\(\theta ∈\) QII
    19. \((−3\sqrt{7}, y)\) \(r = \sqrt{77}\) \ (\ theta\) termina.” >\(\theta ∈\) QIII
    20. \((x, −4\sqrt{5})\) \(r = 3\sqrt{15}\) \ (\ theta\) termina.” >\(\theta ∈\) QIV
    21. \(\left( \dfrac{3}{4} , y \right)\) \(r=1\) \ (\ theta\) termina.” >\(\theta ∈\) QI
    22. \(\left(x, \dfrac{3}{16} \right)\) \(r=1\) \ (\ theta\) termina.” >\(\theta ∈\) QII
    23. \(\left(− \dfrac{\sqrt{5}}{4} , y \right)\) \(r=1\) \ (\ theta\) termina.” >\(\theta ∈\) QIII
    24. \(\left(x, − \dfrac{3\sqrt{2}}{8} \right)\) \(r=1\) \ (\ theta\) termina.” >\(\theta ∈\) QIV

    Para #25 -29, encuentra la fracción de una revolución completa. Después bosquejar el ángulo.

    1. \(\dfrac{1}{4} \cdot 360˚\)
    2. \(\dfrac{1}{2} \cdot 360˚\)
    3. \(\dfrac{3}{4} \cdot 360˚\)
    4. \(\dfrac{1}{8} \cdot 360˚\)
    5. \(\dfrac{1}{6} \cdot 360˚\)

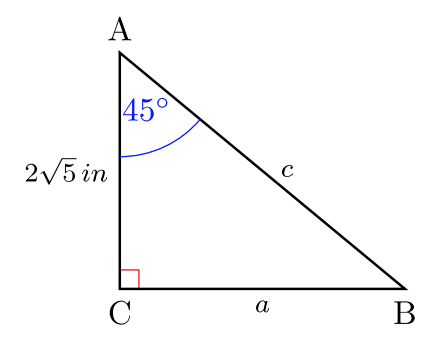
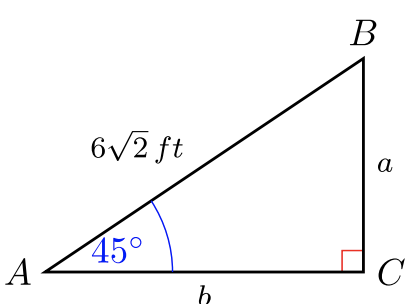
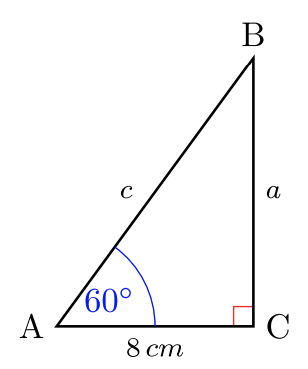
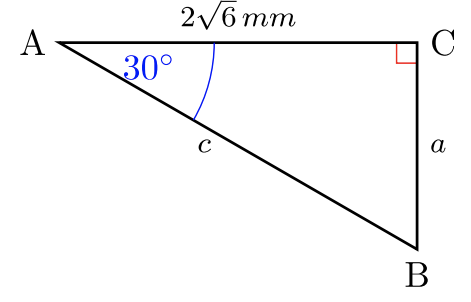
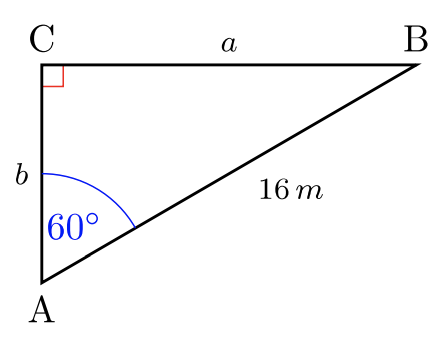
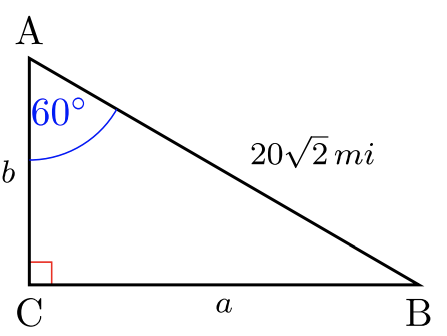
    Para #30 -35, resuelve las longitudes laterales\(2\) faltantes. Dar respuestas exactas. Sin calculadoras.

    1. clipboard_e71a8a05bff7f6a4adc6d5c0b056fc1d7.png
    2. clipboard_ea175eae65ac9e1641c5bbb8d43439f80.png
    3. clipboard_ee446e4e95939c7b67716b36c685644d0.png
    4. clipboard_e4633229195d2f71629d883fc6a786904.png
    5. clipboard_eba2b6dd1020f7ca98f12ad724d338ec6.png
    6. clipboard_e5992c086b12706b09765a4a75c4285a0.png

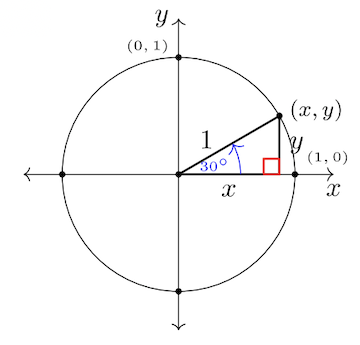
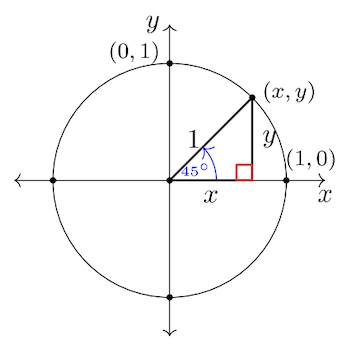
    Para #36 -38, Encuentra las coordenadas del par ordenado\((x, y)\) en el círculo unitario con el ángulo estándar dado. Usa relaciones especiales de triángulo rectángulo. Dar valores exactos de\(x\) y\(y\).

    1. clipboard_ea02e11ad76d1b60bcb971065f6a9a1eb.png
    2. clipboard_ea2c96607cc16568bd33c44e3cc4275ff.png
    3. clipboard_e5da8266361bae60ea0067b4ebef91a12.png

    This page titled 7.1: El Círculo de Unidades is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jennifer Freidenreich.