7.2: Ángulos de referencia

Última actualización
Guardar como PDF

Page ID: 115812

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los Triángulos Recto Especiales,$30˚$$60˚$ - -$90˚$ y$45˚$$45˚$ - -$90˚$, nos permiten obtener valores exactos de los pares ordenados$(x, y)$ en un círculo unitario con ángulos estándar$30˚$,$45˚$, o$60˚$.

Si usamos simetría a través del$y$ eje -y el$x$ eje -eje, podemos poblar los pares ordenados conocidos de QI a los Cuadrantes II, III y IV. Usa las figuras a continuación para seguir cómo se hace esto. Para que las imágenes sean simples,$30˚$ los ángulos están marcados, mientras que$45˚$ y$60˚$ pueden ser conudidos por sus mayores magnitudes.

Figura 7.2.1 : QI → QII$(x, y) → (−x, y)$

Figura 7.2.2 : QII → QIII$(−x, y) → (−x, −y)$

Figura 7.2.3 : QII → QIII$(-x, −y) → (x, −y)$

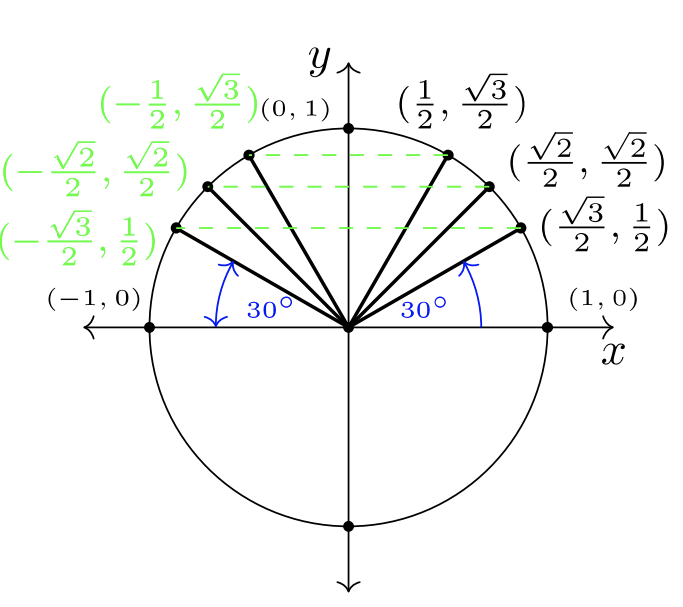
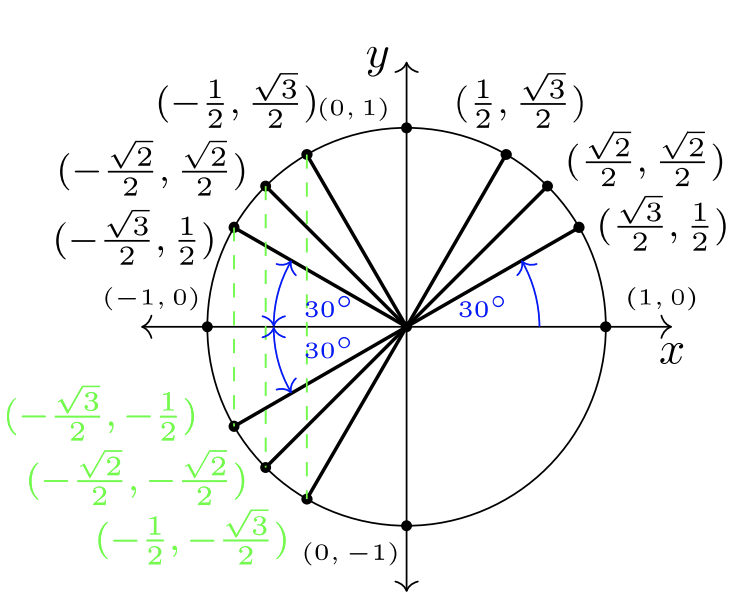
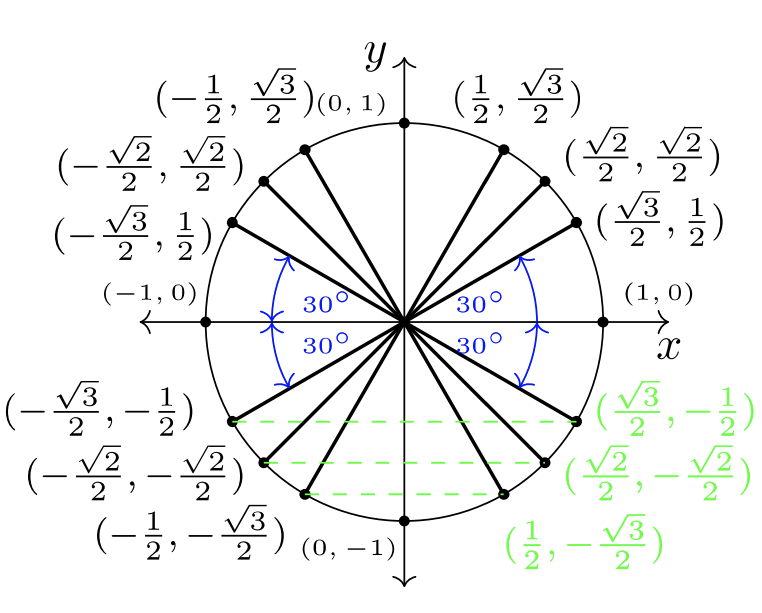
Observe que los cuatro$30˚$ ángulos crean un aspecto de pajarita en la Figura$7.2.3$. Estos ángulos se denominan ángulos de referencia.

Definición: Ángulo de referencia

Dejar$\theta$ ser un ángulo estándar. Un ángulo de referencia$\hat{\theta}$, denotado, es el ángulo agudo positivo entre el lado terminal$\theta$ y el$x$ eje.

Se usa la palabra referencia porque todos los ángulos pueden referirse a QI. Es decir, la memorización de pares ordenados se limita al QI del círculo unitario. Si un ángulo estándar$\theta$ tiene un ángulo de referencia de$30˚$$45˚$, o$60˚$, el par ordenado del círculo unitario se duplica, pero el valor de signo de$x$ o$y$ puede necesitar ajuste, dependiendo del cuadrante del lado terminal de$\theta$.

Ejemplo 7.2.1

El lado terminal de un ángulo estándar$\theta = 225˚$ intersecta el círculo unitario. Indicar el par ordenado de la intersección.

Solución

El círculo unitario tiene radio$r = 1$. La trigonometría combina álgebra y geometría con bocetos visuales. Comenzamos con un boceto del ángulo$\theta = 225˚$. Todos los ángulos estándar comienzan en el lado positivo del$x$ eje. ¿En qué cuadrante está el lado terminal de$\theta$? Es decir, ¿dónde se detiene este ángulo?

¿Dónde está el lado terminal de$\theta = 225˚$? Ya que$180˚ < 225˚ < 270˚$, el lado terminal del ángulo está en QIII.

El ángulo de referencia se calcula encontrando La diferencia entre$225˚$ y$180˚$.

Nota: El ángulo de referencia nunca es negativo.

$|225˚ − 180˚| = |180˚ − 225˚| = \hat{\theta}$

$45˚ = \hat{\theta}$

En QIII, todos los pares ordenados$(x, y)$ son tales que$x < 0$ y$y < 0$. Volviendo a QI, usando el ángulo estándar de$45˚$ en el círculo unitario, el par ordenado$\left( \dfrac{\sqrt{2}}{2} , \dfrac{\sqrt{2}}{2} \right)$ debe ajustarse para negativo$x$ y$y$ coordenadas.

Respuesta El lado terminal de$\theta = 225˚$ cruza el círculo unitario en$\left( −\dfrac{\sqrt{2}}{2} , −\dfrac{\sqrt{2}}{2} \right)$.

Consejo: Cuando un ángulo estándar es mayor que$90˚$, use marcadores$180˚$ o$360˚$ para calcular el ángulo de referencia. ¡Siempre se recomienda dibujar una imagen antes de la computación!

QII:$90˚ < \theta < 180˚$
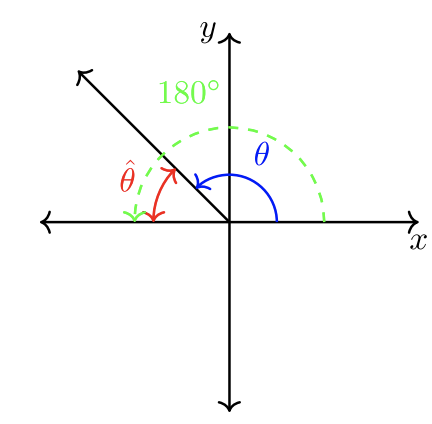
$|180˚ − \theta| = \textcolor{red}{\hat{\theta}}$

QIII:$180˚ < \theta < 270˚$
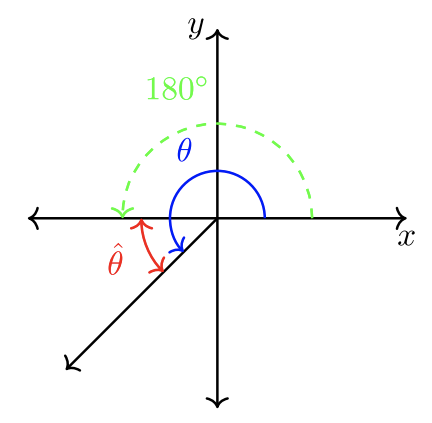
$|180˚ − \theta| = |\theta − 180˚| = \textcolor{red}{\hat{\theta}}$

QIV: Si$270˚ < \theta < 360˚$
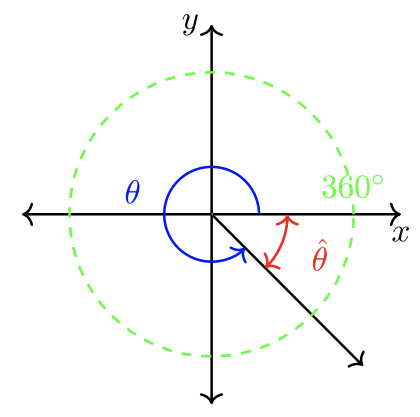
$|360˚ − \theta| = \textcolor{red}{\hat{\theta}}$

Ejemplo 7.2.2

El lado terminal de un ángulo estándar$\theta = −480˚$ intersecta el círculo unitario. Indicar el par ordenado de la intersección.

Solución

Los ángulos negativos giran en sentido horario. Sketch$\theta$. Encuentra un ángulo coterminal positivo:$−480˚ + 360˚(2) = 240˚$ Luego aplica las puntas anteriores o analiza visualmente:$|180˚ − 240˚| = |−60˚| = 60˚ = \hat{\theta}$

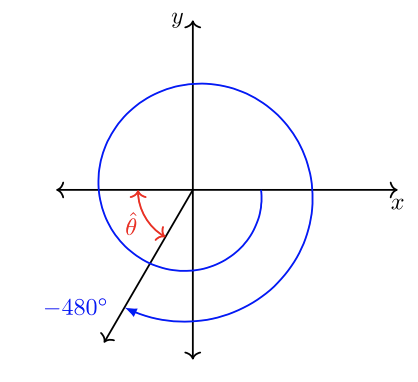
$clipboard_e2e05a1fabdfb42e49534221af0acffe0.png$

El par ordenado en el círculo unitario es$\left(−\dfrac{1}{2} , −\dfrac{\sqrt{3}}{2} \right)$.

¡Pruébalo! (Ejercicios)

Para #1 -10, indicar el ángulo de referencia$\hat{\theta}$,, del ángulo estándar dado.

$\theta = 210˚ $
$\theta = 350˚$
$\theta = 110˚$
$\theta = 240.5˚$
$\theta = 142.75˚$
$\theta = −315˚$
$\theta = −230˚$
$\theta = 500˚$
$\theta = 615˚$
$\theta = −835˚$

Para #11 -20, el lado terminal del ángulo estándar dado,$\theta$, intersecta el círculo unitario en un punto. Indicar el par ordenado de la intersección.

$\theta = 135˚$
$\theta = 300˚$
$\theta = −240˚$
$\theta = −150˚$
$\theta = 420˚$
$\theta = 570˚$
$\theta = 840˚$
$\theta = −765˚$
$\theta = −930˚$
$\theta = 1560˚$

Para #21 -28, la rotación de un ángulo estándar se describe con palabras. Se le dan varias pistas sobre su rotación. Nota: una revolución completa es$360˚$ (en sentido antihorario) o$-360˚$ (en sentido horario). Encuentra la medida del ángulo descrito.

Un ángulo tiene una rotación en sentido antihorario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QIV. El ángulo de referencia$\hat{\theta} = 30˚$.
Un ángulo tiene una rotación en sentido antihorario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QII. El ángulo de referencia$\hat{\theta} = 20˚$.
Un ángulo tiene una rotación en sentido horario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QIII. El ángulo de referencia$\hat{\theta} = 10˚$.
Un ángulo tiene una rotación en sentido horario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QII. El ángulo de referencia$\hat{\theta} = 72˚$.
Un ángulo tiene una rotación en sentido antihorario. El ángulo va más allá de una revolución completa. El lado terminal del ángulo está en QI. El ángulo de referencia$\hat{\theta} = 55˚$.
Un ángulo tiene una rotación en sentido antihorario. El ángulo va más allá de dos revoluciones completas. El lado terminal del ángulo está en QII. El ángulo de referencia$\hat{\theta} = 24˚$.
Un ángulo tiene una rotación en sentido horario. El ángulo va más allá de una revolución completa. El lado terminal del ángulo está en QIII. El ángulo de referencia$\hat{\theta} = 18˚$.
Un ángulo tiene una rotación en sentido horario. El ángulo va más allá de dos revoluciones completas. El lado terminal del ángulo está en QIV. El ángulo de referencia$\hat{\theta} = 39˚$.