7.3: Radianes

Última actualización
Guardar como PDF

Page ID: 115825

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los ángulos se pueden medir en unidades de grados o radianes.

Definición: Radianes

Los radianes son una unidad de medida angular definida de tal manera que

\[2\pi \text{ radians } = 360˚\]

Para los astutos de corazón, se puede crear$1$ un ángulo de radián con un círculo (use cualquier tapa de un frasco) y un trozo de cuerda.

Figura 7.3.1 : Desde el centro del círculo, coloque su cadena hacia abajo para crear un radio. Después corta la cuerda al tamaño de su radio. Medida de cadena = medida de radio

Figura 7.3.2 : A continuación, toma la cuerda cortada y pégala al borde del círculo. El centro del círculo es el vértice del ángulo. Conecte los extremos de las cadenas al centro del círculo. ¡El ángulo es un radián!

Recordemos que la circunferencia de un círculo (que es el perímetro de un círculo) tiene una fórmula:

Circunferencia =$C = 2 \pi r$ donde$r =$ radio del círculo

¿Cuántas cuerdas de longitud$r$ se necesitan para envolver todo el círculo? Dividimos las$r$ formas de circunferencia:$\dfrac{2 \pi r}{r} = 2 \pi ≈ 6$. Acerca de$6$ cadenas de longitud$r$, o exactamente$2 \pi$ cuerdas.

La rotación de un ángulo en sentido antihorario se puede medir como una fracción de una rotación completa.

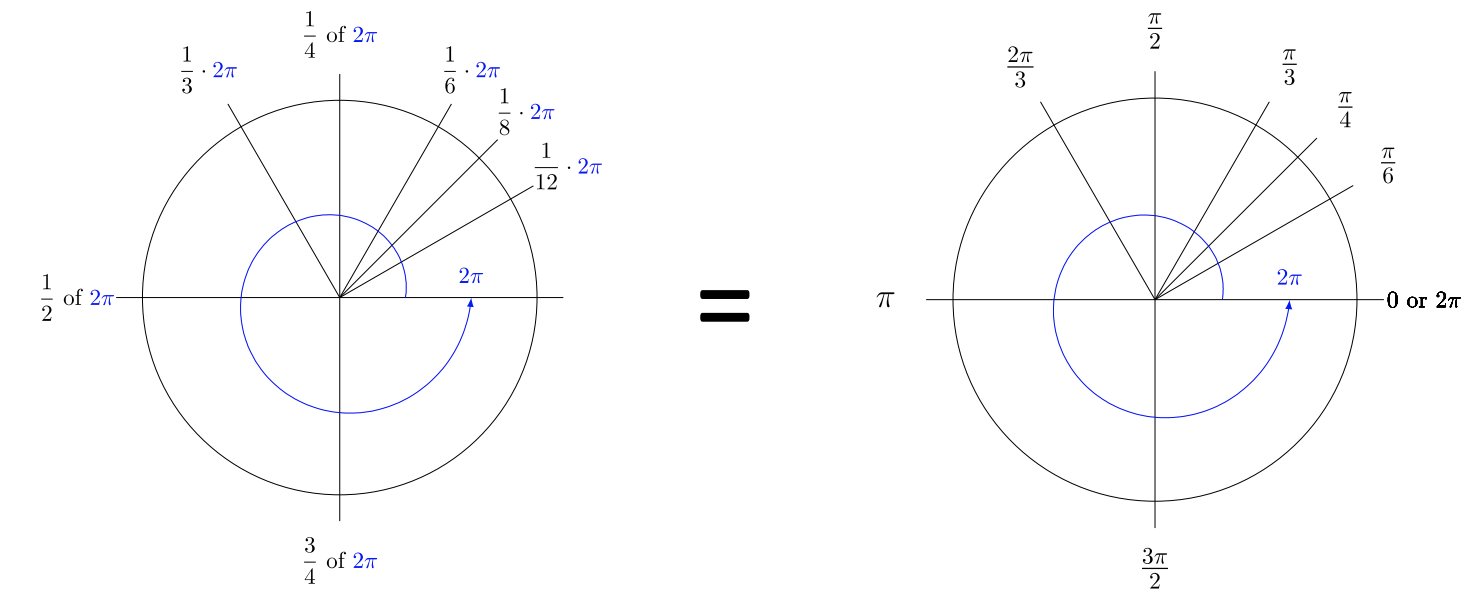
$clipboard_e96d16ca2fe5ce83c85f3fb2b53c3d2f1.png$

Una vez que captas la caída de los radianes, tus cálculos trigonométricos son rápidos y fáciles. El uso de radianes para los ángulos, en lugar de grados, es la clave para ganar fluidez en la trigonometría. Son más simples de usar que los grados. Observe los denominadores compartidos de un cuadrante al siguiente. También observe que el denominador de un ángulo coincide con el denominador de su propio ángulo de referencia.

$30˚ = \dfrac{\pi}{6} \text{ radians } \;\;\;\;\;\;\;\;\;\;\;\;\; 45˚ = \dfrac{\pi}{4} \text{ radians } \;\;\;\;\;\;\;\;\;\;\;\;\; 60˚ = \dfrac{\pi}{3} \text{ radians }$

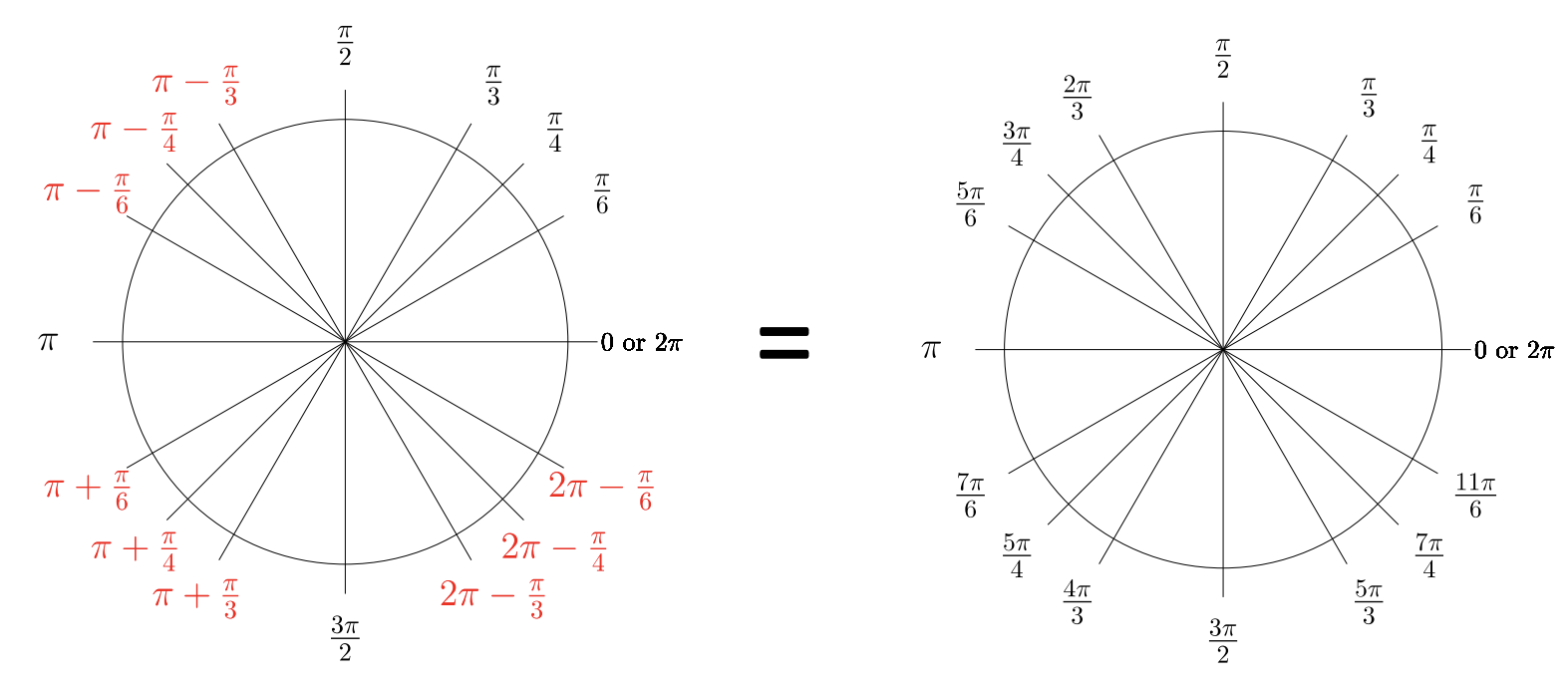
$clipboard_e457d0698b87a6baf0f73f29c9f690168.png$

Los ángulos de referencia se refieren al QI, donde entra en juego tu memorización. Memorice solo QI y los pares ordenados del círculo unitario en ese cuadrante (ver Sección 7.2). ¡Evita memorizar demasiado! Usa cálculos intuitivos para ensayar conceptos matemáticos. Si un valor de radianes no es uno de los valores anteriores, ni coterminal a los mostrados, entonces necesitará una calculadora para cálculos trigonométricos.

Ejemplo 7.3.1

Indique el ángulo de referencia$\hat{\theta}$ (en radianes) para el ángulo estándar dado$\theta$. Después bosquejar ambos$\theta$ y$\hat{\theta}$.

$\theta = \dfrac{7 \pi}{6}$
$\theta = − \dfrac{2 \pi}{3}$
$\theta = \dfrac{11 \pi}{4}$
$\theta = 6 \text{ radians}$

Solución

$\theta = \dfrac{7 \pi}{6}$. Decidir si$\dfrac{7 \pi}{6}$ está más cerca$\pi$ o$2 \pi$.

Desde$\pi = \dfrac{6\pi}{6}$ y$2\pi = \dfrac{12\pi}{6}$, es claro eso$\dfrac{7\pi}{6} > \dfrac{6\pi}{6}$ y más cerca de$\pi$.

El ángulo de referencia es$\hat{\theta} = \dfrac{\pi}{6}$.

$\dfrac{7\pi}{6} = \pi + \dfrac{\pi}{6}$.

El boceto se muestra a continuación.

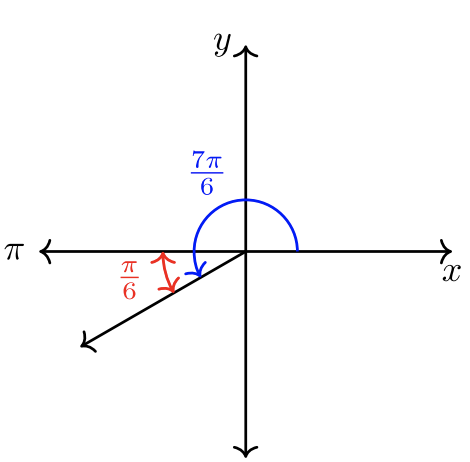
$clipboard_e758796aa951c3dfbb9b7bcb8144753ea.png$

$\theta = − \dfrac{2 \pi}{3}$. El ángulo gira en sentido horario.

$\left|− \dfrac{2\pi}{3} \right| = \dfrac{2\pi}{3}$que termina en la QII.

La rotación en sentido horario de$−\dfrac{2\pi}{3}$ termina en QIII.

Ambos$\dfrac{2\pi}{3}$ y$−\dfrac{2\pi}{3}$ tienen el mismo ángulo de referencia.

$\hat{\theta} = \dfrac{\pi}{3}$.

El boceto se muestra a continuación.

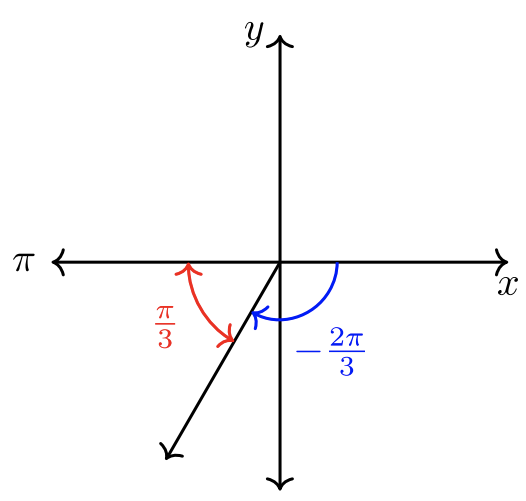
$clipboard_e2ce08b292bebde15a1d77ac730a8e8fe.png$

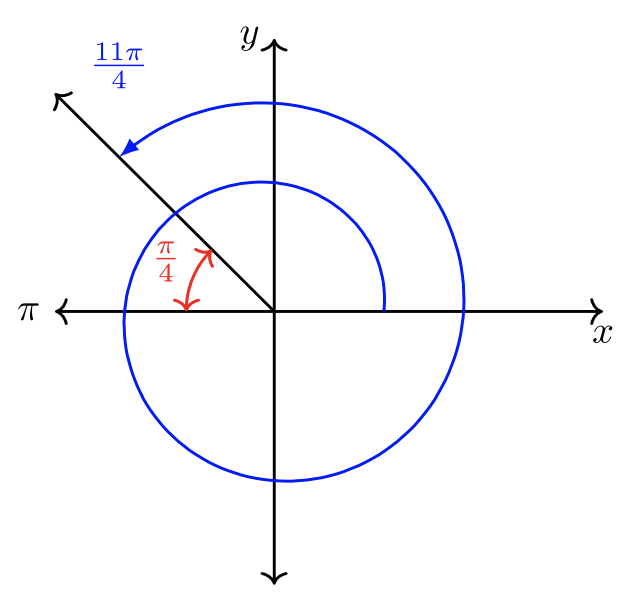
$\theta = \dfrac{11 \pi}{4}$. El denominador es$4$.

Desde$\dfrac{8\pi}{4} = 2\pi$ y$\dfrac{11\pi}{4} > \dfrac{8\pi}{4}$, este ángulo gira más allá de una revolución completa. $\pi$es coterminal con$3\pi$,$5\pi$,$7\pi$... mientras que$2\pi$ es coterminal con$4\pi$,$6\pi$,$8\pi$,...

Comparar$\dfrac{11\pi}{4}$ con$3\pi = \dfrac{12\pi}{4}$. ¡Están muy cerca en valor! $\dfrac{11\pi}{4} < \dfrac{12\pi}{4}$y$\dfrac{11\pi}{4}$ por lo tanto termina en la QII. El ángulo de referencia$\hat{\theta} = \dfrac{\pi}{4}$.

A continuación se muestra el boceto del ángulo.

$clipboard_eed9b1562a948efe6edfab78d67e05c3b.png$

$\theta = 6 \text{ radians}$. Decidir si$6$ los radianes están más cerca$\pi$ o$2\pi$.

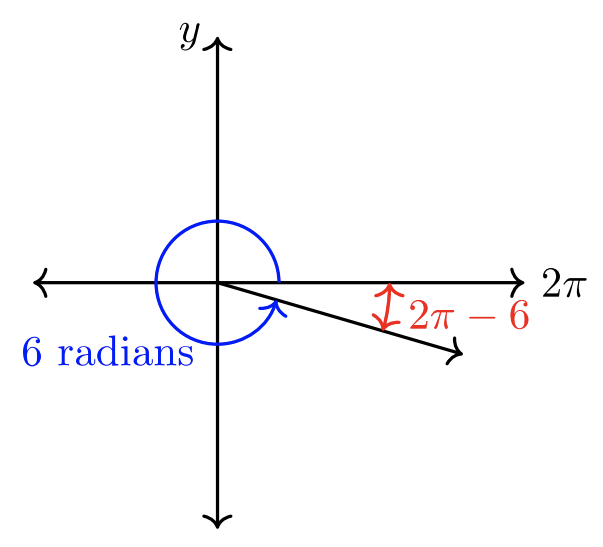
Desde$\pi ≈ 3.14$ y$2\pi ≈ 6.28$,$6$ radianes está más cerca de$2\pi$. $6 < 2\pi$, por lo tanto el ángulo termina en QIV.

El ángulo de referencia$\hat{\theta} = 2\pi − 6 ≈ 0.28$ radianes.

A continuación se muestra el boceto del ángulo.

$clipboard_ee7bece9679fcef2edbf41c496f299d1e.png$

Ejemplo 7.3.2

El lado terminal de un$\theta = \dfrac{3\pi}{4}$ radianes de ángulo estándar intersecta el círculo unitario. Indicar el par ordenado de la intersección.

Solución

Ya que$\dfrac{3\pi}{4} = \dfrac{4\pi}{4} − \dfrac{\pi}{4}$, el ángulo$\theta = \dfrac{3\pi}{4}$ termina en QII con ángulo de referencia$\hat{\theta} = \dfrac{\pi}{4}$.

El círculo unitario se introdujo en la Sección 7.2 para ángulos de grados. La figura que se muestra a continuación incluye ángulos radianes.

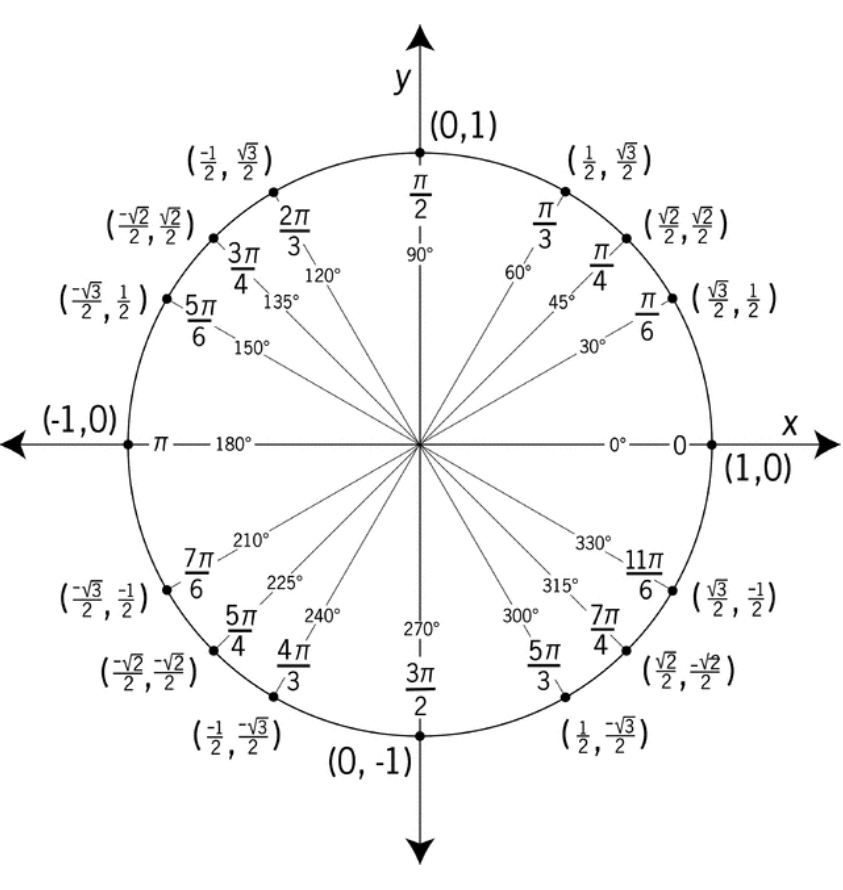
$clipboard_edf7f7bacee9db4fb14db4c139a3b04c1.png$

El par ordenado en el círculo unitario, intersectando el lado terminal de$\pi = \dfrac{3\pi}{4}$ es$\left(−\dfrac{\sqrt{2}}{2} , \dfrac{\sqrt{2}}{2} \right)$.

Ejemplo 7.3.3

El lado terminal de un$\theta = \dfrac{5\pi}{2}$ radianes de ángulo estándar intersecta el círculo unitario. Indicar el par ordenado de la intersección.

Solución

Ya que$\dfrac{5\pi}{2} = \dfrac{\pi}{2} + 2\pi$, los ángulos$\dfrac{5\pi}{2}$ y$\dfrac{\pi}{2}$ son ángulos coterminales. Los ángulos coterminales aterrizan en el mismo lugar, por lo que el par ordenado será el mismo. El par ordenado en el círculo unitario, intersectando el lado terminal de$\theta = \dfrac{5\pi}{2}$ es$(0, 1)$.

Ejemplo 7.3.4

El lado terminal de un$\theta = 10\pi$ radianes de ángulo estándar intersecta el círculo unitario. Indicar el par ordenado de la intersección.

Solución

Ya que$10\pi = 2\pi(5)$, los ángulos$10\pi$ y$2\pi$ son ángulos coterminales. Por lo tanto, el par ordenado en el círculo unitario, intersectando el lado terminal de$\theta = 10\pi$ es$(1, 0)$.

¡Pruébalo! (Ejercicios)

Para #1 -10,$\theta$ se da un ángulo estándar en radianes. Indicar el ángulo de referencia$\hat{\theta}$ en radianes.

$\theta = \dfrac{11\pi}{6}$
$\theta = \dfrac{7\pi}{9}$
$\theta = \dfrac{11\pi}{7}$
$\theta = 2$radianes
$\theta = −\dfrac{5\pi}{6}$
$\theta = −\dfrac{5\pi}{4}$
$\theta = \dfrac{9\pi}{4}$
$\theta = \dfrac{17\pi}{6}$
$\theta = 10$radianes
$\theta = −\dfrac{6\pi}{5}$

Para #11 -20, el lado terminal del ángulo estándar dado,$\theta$, intersecta el círculo unitario en un punto. Indicar el par ordenado de la intersección.

$\theta = \dfrac{7\pi}{6}$
$\theta = \dfrac{4\pi}{3}$
$\theta = \dfrac{11\pi}{3}$
$\theta = \dfrac{7\pi}{2}$
$\theta = 5\pi$
$\theta = \dfrac{13\pi}{4}$
$\theta = −\dfrac{7\pi}{6}$
$\theta = −4\pi$
$\theta = −\dfrac{11\pi}{4}$
$\theta = −\dfrac{5\pi}{2}$

Para #21 -27, la rotación de un ángulo estándar se describe con palabras. Se le dan varias pistas sobre su rotación. Nota: una revolución completa son$2\pi$ radianes (si en sentido contrario a las agujas del reloj) o$−2\pi$ radianes (si en sentido horario). Encuentra la medida del ángulo descrito usando radianes.

Un ángulo tiene una rotación en sentido antihorario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QIII. El ángulo de referencia$\hat{\theta} = \dfrac{\pi}{3}$.
Un ángulo tiene una rotación en sentido antihorario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QIV. El ángulo de referencia$\hat{\theta} = \dfrac{\pi}{4}$.
Un ángulo tiene una rotación en sentido antihorario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QII. El ángulo de referencia$\hat{\theta} = \dfrac{\pi}{6}$.
Un ángulo tiene una rotación en sentido horario. El ángulo no hace una revolución completa. El lado terminal del ángulo está en QIV. El ángulo de referencia$\hat{\theta} = \dfrac{\pi}{3}$.
Un ángulo tiene una rotación en sentido horario. El ángulo no hace una revolución completa. El lado terminal del ángulo intersecta el círculo unitario en el punto$(−1, 0)$.
Un ángulo tiene una rotación en sentido antihorario. El ángulo gira más de una revolución completa. El lado terminal del ángulo intersecta el círculo unitario en el punto$\left(−\dfrac{\sqrt{2}}{2}, −\dfrac{\sqrt{2}}{2} \right)$.
Un ángulo tiene una rotación en sentido antihorario. El ángulo gira más de dos revoluciones completas. El lado terminal del ángulo intersecta el círculo unitario en el punto$\left(−\dfrac{1}{2} , \dfrac{\sqrt{3}}{2} \right)$.