6.4: Ecuaciones logarítmicas y desigualdades

En la Sección 6.3 resolvemos ecuaciones y desigualdades que involucran funciones exponenciales utilizando una de dos estrategias básicas. Ahora dirigimos nuestra atención a ecuaciones y desigualdades que involucran funciones logarítmicas, y no es sorprendente que haya dos estrategias básicas para elegir. Por ejemplo, supongamos que deseamos resolver\(\log_{2}(x) = \log_{2}(5)\). El teorema 6.4 nos dice que la única solución a esta ecuación es\(x=5\). Ahora supongamos que deseamos resolver\(\log_{2}(x) = 3\). Si queremos usar el Teorema 6.4, necesitamos reescribir\(3\) como base logarítmica\(2\). Podemos usar el Teorema 6.3 para hacer precisamente eso:\(3 = \log_{2}\left(2^{3}\right) = \log_{2}(8)\). Nuestra ecuación entonces se vuelve\(\log_{2}(x) = \log_{2}(8)\) así\(x = 8\). Sin embargo, podríamos haber llegado a la misma respuesta, en menos pasos, usando el Teorema 6.3 para reescribir la ecuación\(\log_{2}(x) = 3\) como\(2^{3} = x\), o\(x=8\). A continuación resumimos las dos formas comunes de resolver ecuaciones logarítmicas.

Pasos para resolver una ecuación que involucra funciones logarítmicas

1. Aislar la función logarítmica.
2. 1. Si es conveniente, exprese ambos lados como registros con la misma base e iguale los argumentos de las funciones de registro.
   2. De lo contrario, reescriba la ecuación logarítmica como una ecuación exponencial.

Ejemplo 6.4.1

1. \(\log_{117}(1-3x) = \log_{117}\left(x^2-3\right)\)
2. \(2 - \ln(x-3) = 1\)
3. \(\log_{6}(x+4) + \log_{6}(3-x) = 1\)
4. \(\log_{7}(1-2x) = 1 - \log_{7}(3-x)\)
5. \(\log_{2}(x+3) = \log_{2}(6-x)+3\)
6. \(1 + 2 \log_{4}(x+1) = 2 \log_{2}(x)\)

Solución.

1. Como tenemos la misma base en ambos lados de la ecuación\(\log_{117}(1-3x) = \log_{117}\left(x^2-3\right)\), equiparamos lo que hay dentro de los registros para obtener\(1-3x = x^2-3\). Resolviendo\(x^2+3x-4 = 0\) da\(x=-4\) y\(x=1\). Para verificar estas respuestas usando la calculadora, hacemos uso del cambio de fórmula base y gráfica\(f(x) = \frac{\ln(1-3x)}{\ln(117)}\)\(g(x) = \frac{\ln\left(x^2-3\right)}{\ln(117)}\) y vemos que se cruzan solo en\(x=-4\). Para ver qué pasó con la solución\(x=1\), la sustituimos en nuestra ecuación original para obtener\(\log_{117}(-2) = \log_{117}(-2)\). Si bien estas expresiones se ven idénticas, tampoco lo es un número real, ¹ lo que significa que no\(x=1\) está en el dominio de la ecuación original, y no es una solución.
2. Nuestro primer objetivo en la resolución\(2 - \ln(x-3) = 1\) es aislar el logaritmo. Obtenemos\(\ln(x-3)=1\), que, como ecuación exponencial, es\(e^{1} = x-3\). Obtenemos nuestra solución\(x=e+3\). En la calculadora, vemos la gráfica de\(f(x) = 2 - \ln(x-3)\) cruza la gráfica de\(g(x) = 1\) at\(x = e+3 \approx 5.718\).

   

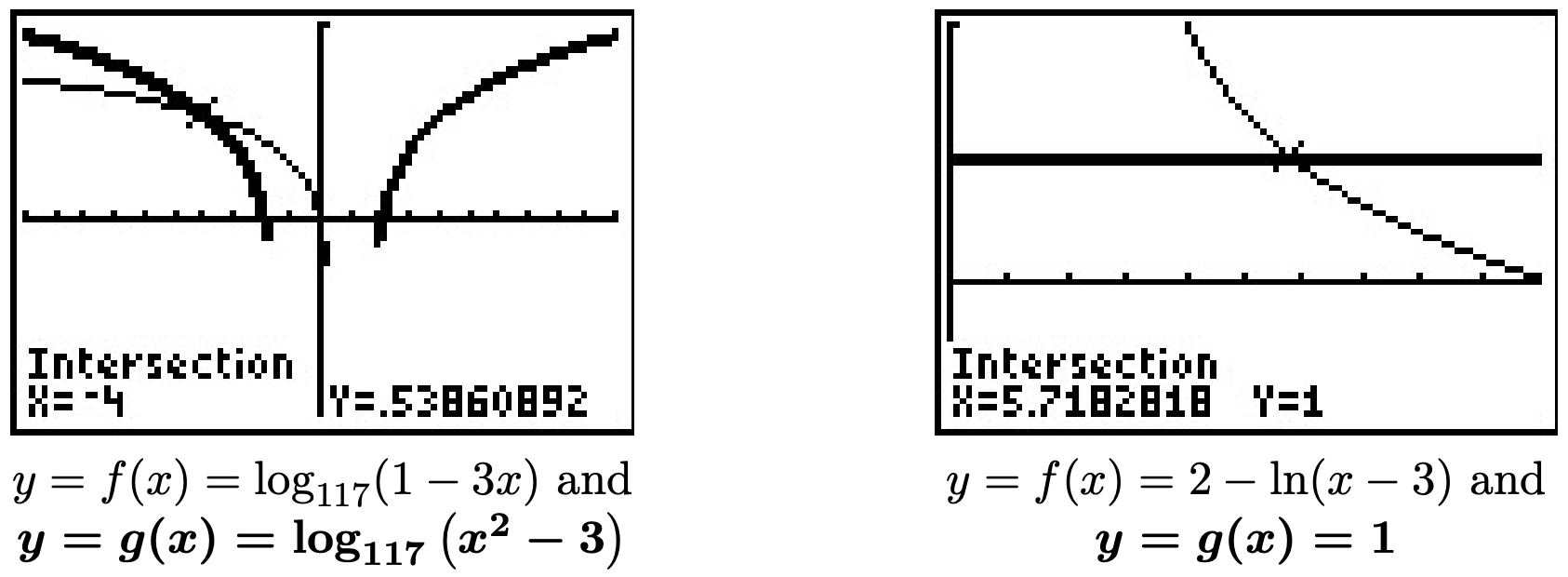
3. Podemos comenzar a resolver\(\log_{6}(x+4) + \log_{6}(3-x) = 1\) usando la Regla de Producto para logaritmos para reescribir la ecuación como\(\log_{6}\left[(x+4)(3-x)\right] = 1\). Reescribiendo esto como una ecuación exponencial, obtenemos\(6^{1} = (x+4)(3-x)\). Esto se reduce a\(x^2+x-6 = 0\), lo que da\(x=-3\) y\(x=2\). Graficando\(y=f(x) = \frac{\ln(x+4)}{\ln(6)} + \frac{\ln(3-x)}{\ln(6)}\) y\(y=g(x) = 1\), vemos que se cruzan dos veces, en\(x=-3\) y\(x=2\).

   

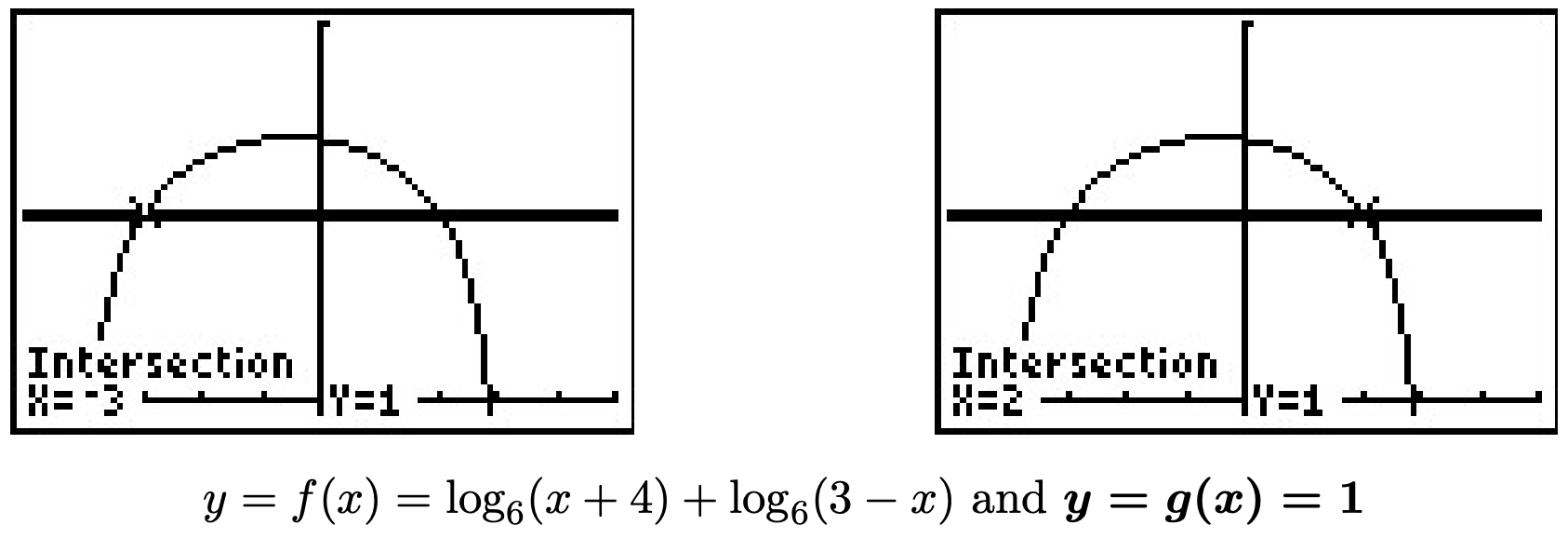
4. Siguiendo el ejemplo del problema anterior, comenzamos a resolver\(\log_{7}(1-2x) = 1 - \log_{7}(3-x)\) primero recolectando los logaritmos del mismo lado\(\log_{7}(1-2x) + \log_{7}(3-x) = 1\), y luego usando la Regla del Producto para obtener\(\log_{7}[(1-2x)(3-x)] = 1\). Reescribir esto como una ecuación exponencial da\(7^{1} = (1-2x)(3-x)\) lo que da la ecuación cuadrática\(2x^2-7x-4=0\). Resolviendo, encontramos\(x = -\frac{1}{2}\) y\(x=4\). Graficando, encontramos\(y = f(x) = \frac{\ln(1-2x)}{\ln(7)}\) e\(y=g(x) = 1 - \frac{\ln(3-x)}{\ln(7)}\) intersectamos solo en\(x=-\frac{1}{2}\). Comprobando\(x=4\) la ecuación original produce\(\log_{7}(-7) = 1 - \log_{7}(-1)\), lo cual es una clara violación de dominio.
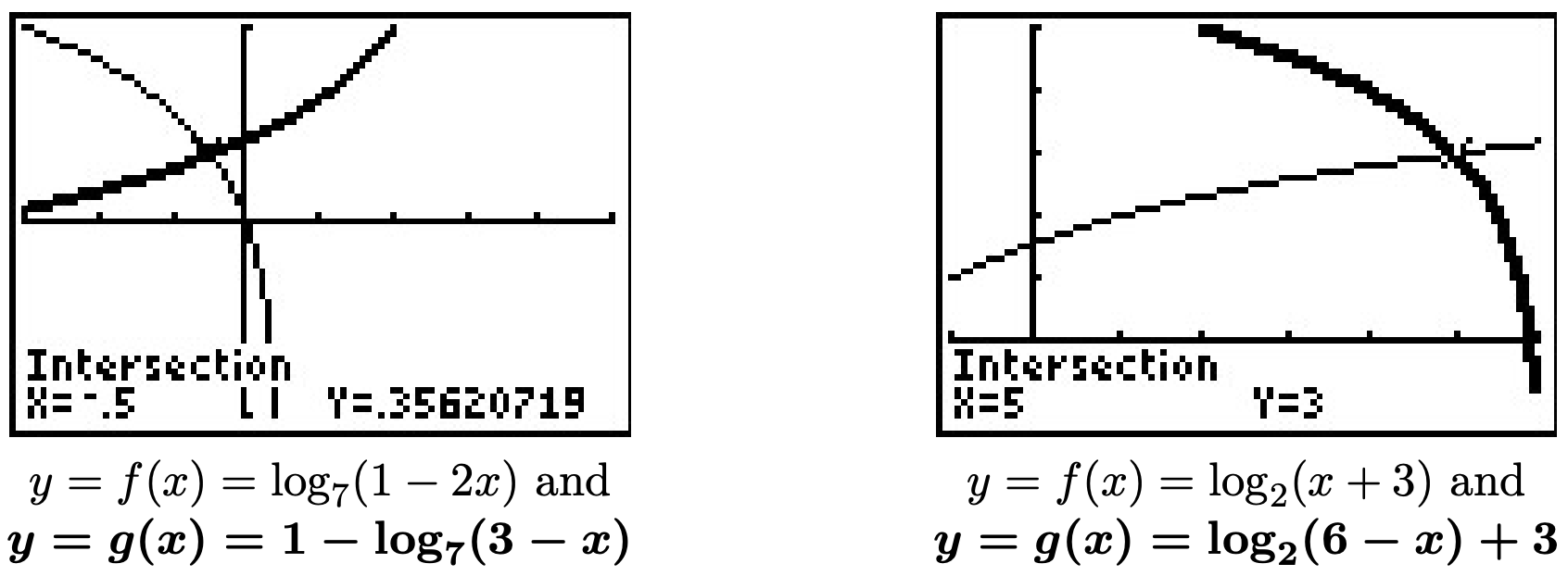
5. Empezando por\(\log_{2}(x+3) = \log_{2}(6-x)+3\), recogemos los logaritmos a un lado y conseguimos\(\log_{2}(x+3) - \log_{2}(6-x) = 3\). Luego usamos la Regla del Cociente y convertimos a una ecuación exponencial\[\log_{2}\left(\frac{x+3}{6-x}\right) = 3 \iff 2^{3} = \frac{x+3}{6-x}\nonumber\] Esto se reduce a la ecuación lineal\(8(6-x) = x+3\), que nos da\(x = 5\). Cuando graficamos\(f(x) = \frac{\ln(x+3)}{\ln(2)}\) y\(g(x) = \frac{\ln(6-x)}{\ln(2)} + 3\), encontramos que se cruzan en\(x=5\).

   

6. Empezando por\(1 + 2 \log_{4}(x+1) = 2 \log_{2}(x)\), reunimos los troncos a un lado para obtener la ecuación\(1 = 2 \log_{2}(x) - 2 \log_{4}(x+1)\). Antes de poder combinar los logaritmos, sin embargo, necesitamos una base común. Ya que\(4\) es un poder de\(2\), usamos cambio de base para convertir\[\log_{4}(x+1) = \frac{\log_{2}(x+1)}{\log_{2}(4)} = \frac{1}{2} \log_{2}(x+1)\nonumber\] De ahí, nuestra ecuación original se convierte

   \[\begin{array}{rclr} 1 & = & 2 \log_{2}(x) - 2 \left(\frac{1}{2} \log_{2}(x+1)\right) & \\[4pt] 1 &= & 2\log_{2}(x) - \log_{2}(x+1) & \\[4pt] 1 & = & \log_{2}\left(x^2\right) - \log_{2}(x+1) & \text{Power Rule} \\[4pt] 1 & = & \log_{2}\left( \dfrac{x^{2}}{x+1}\right) & \text{Quotient Rule} \\ \end{array}\nonumber\]

   Reescribiendo esto en forma exponencial, obtenemos\(\frac{x^{2}}{x+1} = 2\) o\(x^2 -2x-2 = 0\). Usando la fórmula cuadrática, obtenemos\(x = 1 \pm \sqrt{3}\). Graficando\(f(x) = 1 + \frac{2\ln(x+1)}{\ln(4)}\) y\(g(x) = \frac{2 \ln(x)}{\ln(2)}\), vemos que las gráficas se cruzan solo en\(x = 1 + \sqrt{3} \approx 2.732\). La solución\(x = 1 - \sqrt{3} < 0\), lo que significa que si se sustituye en la ecuación original, el término\(2 \log_{2}\left(1 - \sqrt{3}\right)\) es indefinido.

   

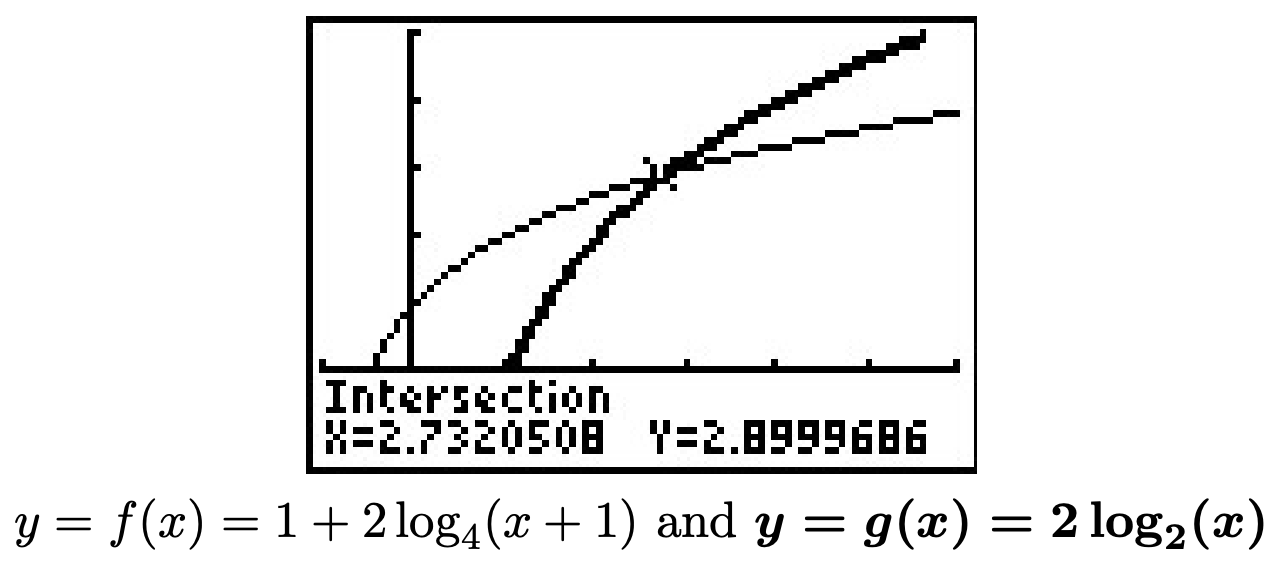
Si nada más, el Ejemplo 6.4.1 demuestra la importancia de verificar soluciones extrañas ² al resolver ecuaciones que involucran logaritmos. Aunque comprobamos nuestras respuestas gráficamente, las soluciones extrañas son fáciles de detectar; cualquier supuesta solución que cause un número negativo dentro de un logaritmo debe descartarse. Al igual que con las ecuaciones del Ejemplo 6.3.1, se puede aprender mucho comprobando analíticamente todas las respuestas del Ejemplo 6.4.1. Dejamos esto al lector y dirigimos nuestra atención a las desigualdades que involucran funciones logarítmicas. Dado que las funciones logarítmicas son continuas en sus dominios, podemos usar diagramas de signos.

Ejemplo 6.4.2

Resolver las siguientes desigualdades. Verifica tu respuesta gráficamente usando una calculadora.

1. \(\dfrac{1}{\ln(x)+1} \leq 1\)
2. \(\left(\log_{2}(x)\right)^2 < 2 \log_{2}(x) + 3\)
3. \(x \log(x+1) \geq x\)

Solución.

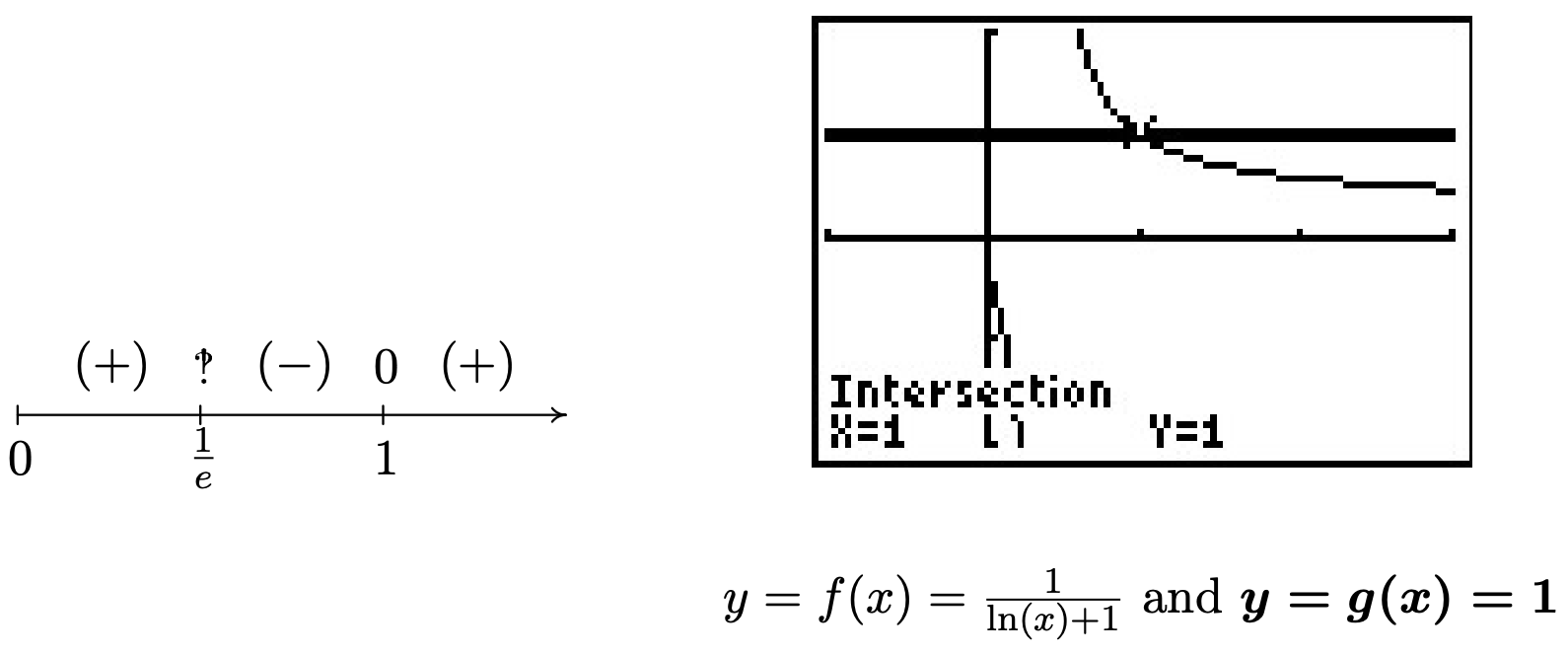
1. Empezamos a resolver\(\frac{1}{\ln(x)+1} \leq 1\)\(0\) poniéndonos de un lado de la desigualdad:\(\frac{1}{\ln(x)+1} - 1 \leq 0\). Obtener un denominador común rinde\(\frac{1}{\ln(x)+1} - \frac{\ln(x)+1}{\ln(x)+1} \leq 0\) lo que reduce a\(\frac{-\ln(x)}{\ln(x)+1} \leq 0\), o\(\frac{\ln(x)}{\ln(x)+1} \geq 0\). Definimos\(r(x) = \frac{\ln(x)}{\ln(x)+1}\) y nos fijamos en encontrar el dominio y los ceros de\(r\). Debido a la aparición del término\(\ln(x)\), requerimos\(x > 0\). Para mantener el denominador alejado de cero,\(\ln(x)+1 = 0\) lo resolvemos así\(\ln(x) = -1\), así\(x = e^{-1} = \frac{1}{e}\). De ahí que el dominio de\(r\) es\(\left(0, \frac{1}{e}\right) \cup \left(\frac{1}{e}, \infty\right)\). Para encontrar los ceros de\(r\), nos fijamos de\(r(x) = \frac{\ln(x)}{\ln(x)+1} = 0\) manera que\(\ln(x) = 0\), y nos encontramos\(x = e^{0} = 1\). Para determinar los valores de prueba para\(r\) sin recurrir a la calculadora, necesitamos encontrar números entre\(0\),\(\frac{1}{e}\), y\(1\) que tengan una base de\(e\). Ya que\(e \approx 2.718 > 1\),\(0 < \frac{1}{e^2} < \frac{1}{e} < \frac{1}{\sqrt{e}} < 1 < e\). Para determinar el signo de\(r\left( \frac{1}{e^2} \right)\), utilizamos el hecho de que\(\ln\left(\frac{1}{e^2}\right) = \ln\left(e^{-2}\right) = -2\), y encontrar\(r\left( \frac{1}{e^2} \right) = \frac{-2}{-2+1} = 2\), cual es\((+)\). El resto de los valores de prueba se determinan de manera similar. A partir de nuestro diagrama de señales, encontramos la solución para ser\(\left(0, \frac{1}{e}\right) \cup [1, \infty)\). Graficando\(f(x) = \frac{1}{\ln(x)+1}\) y\(g(x) = 1\), vemos que la gráfica de\(f\) está debajo de la gráfica de\(g\) en los intervalos de solución, y que las gráficas se cruzan en\(x=1\).

   

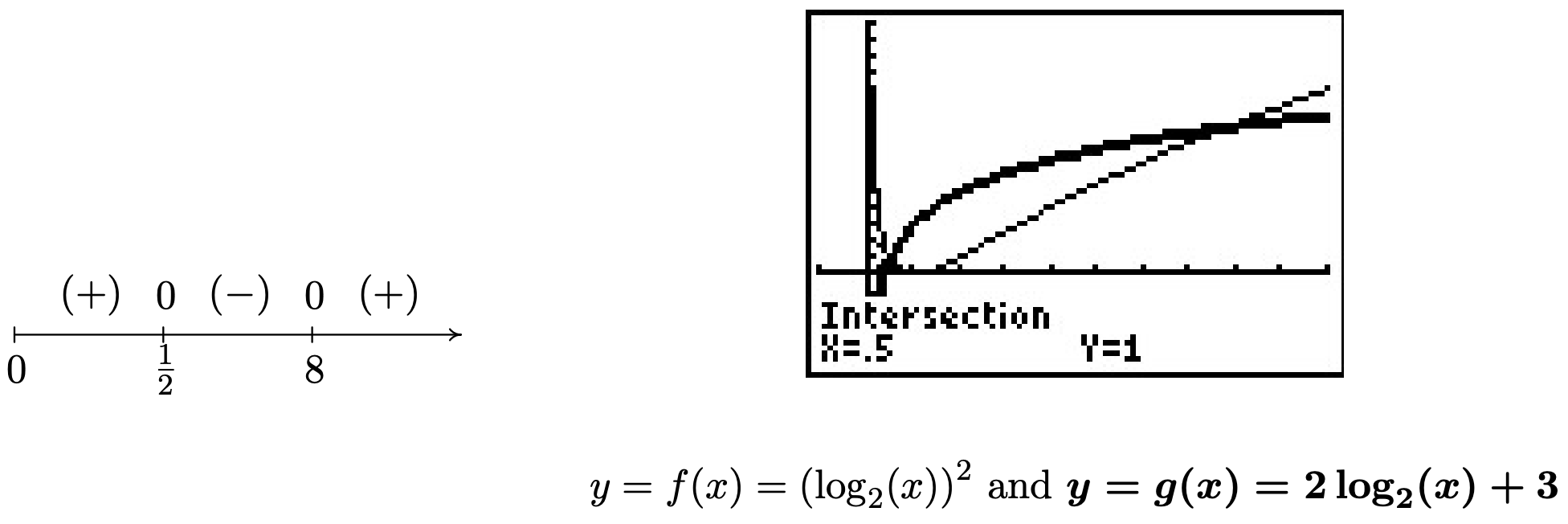
2. Moviendo todos los términos distintos de cero de\(\left(\log_{2}(x)\right)^2 < 2 \log_{2}(x) + 3\) a un lado de la desigualdad, tenemos\(\left(\log_{2}(x)\right)^2 - 2 \log_{2}(x) - 3 < 0\). Definiendo\(r(x) = \left(\log_{2}(x)\right)^2 - 2 \log_{2}(x) - 3\), obtenemos el dominio de\(r\) es\((0, \infty)\), debido a la presencia del logaritmo. Para encontrar los ceros de\(r\), establecemos\(r(x) =\left(\log_{2}(x)\right)^2 - 2 \log_{2}(x) - 3= 0\) lo que resulta en un 'cuadrático disfrazado'. Nos fijamos\(u = \log_{2}(x)\) así nuestra ecuación se convierte en\(u^2-2u-3 = 0\) la que nos da\(u=-1\) y\(u=3\). Ya que\(u = \log_{2}(x)\), obtenemos\(\log_{2}(x) = -1\), que nos da\(x = 2^{-1} = \frac{1}{2}\), y\(\log_{2}(x) = 3\), que rinde\(x = 2^{3} = 8\). Utilizamos valores de prueba que son potencias de\(2\):\(0 < \frac{1}{4} < \frac{1}{2} < 1 < 8 < 16\), y de nuestro diagrama de signos, vemos\(r(x)< 0\) en\(\left(\frac{1}{2}, 8 \right)\). Geométricamente, vemos que la gráfica de\(f(x)= \left(\frac{\ln(x)}{\ln(2)}\right)^2\) está debajo de la gráfica de\(y = g(x) = \frac{2 \ln(x)}{\ln(2)} + 3\) en el intervalo de solución.

   

3. Empezamos a resolver\(x \log(x+1) \geq x\) restando\(x\) de ambos lados para conseguir\(x \log(x+1) - x \geq 0\). Definimos\(r(x) = x \log(x+1) - x\) y debido a la presencia del logaritmo, requerimos\(x+1 > 0\), o\(x > -1\). Para encontrar los ceros de\(r\), nos fijamos\(r(x) = x \log(x+1) - x = 0\). Factoring, obtenemos\(x \left(\log(x+1) - 1\right) = 0\), que da\(x=0\) o\(\log(x+1) - 1=0\). Este último da\(\log(x+1) = 1\), o\(x+1 = 10^{1}\), que admite\(x = 9\). Seleccionamos valores de prueba\(x\) para que\(x+1\) sea una potencia de\(10\), y obtenemos\(-1 < -0.9 < 0 < \sqrt{10} -1 < 9 < 99\). Nuestro diagrama de señales da la solución a ser\((-1,0] \cup [9, \infty)\). La calculadora indica que la gráfica de\(y= f(x) = x \log(x+1)\) está arriba\(y=g(x) = x\) en los intervalos de solución, y las gráficas se cruzan en\(x=0\) y\(x=9\).

   

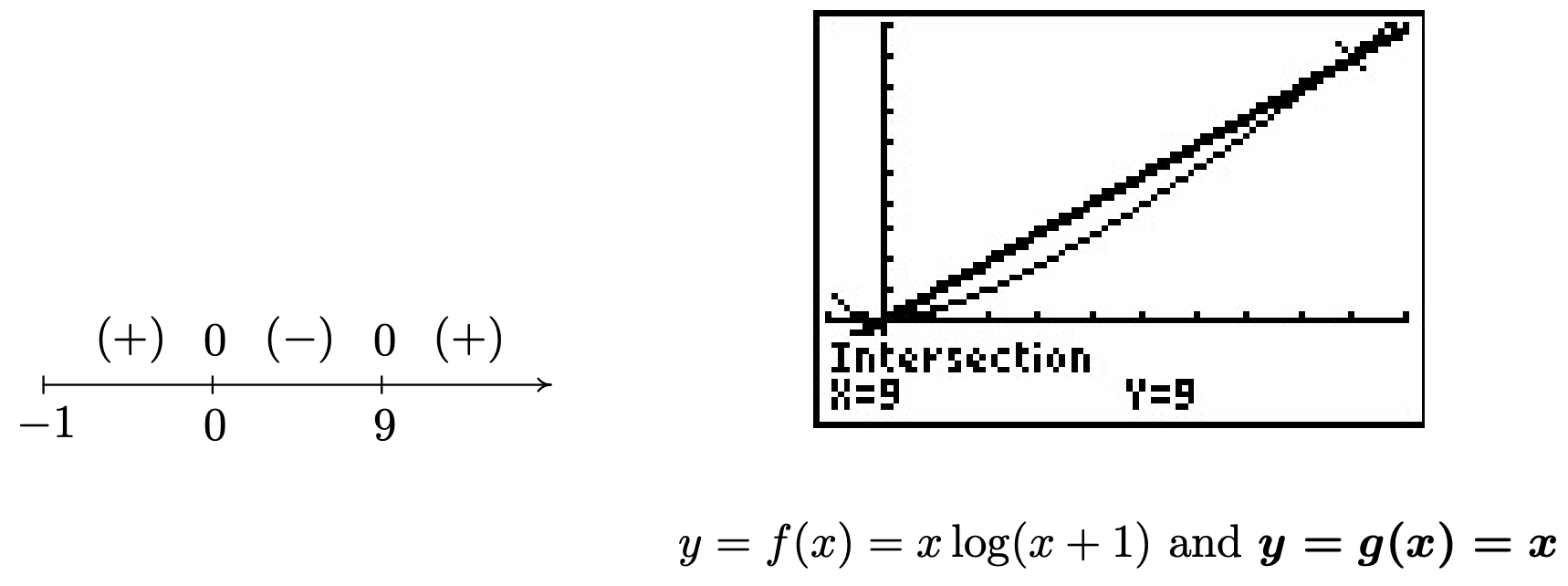
Nuestro siguiente ejemplo vuelve a examinar el concepto de pH visto por primera vez en el Ejercicio 77 en la Sección 6.1.

Ejemplo 6.4.3

Para criar con éxito peces Ippizuti el pH de un tanque de agua dulce debe ser de al menos 7.8 pero no puede ser superior a 8.5. Determine el rango correspondiente de concentración de iones de hidrógeno y verifique su respuesta usando una calculadora.

Solución

Recordemos del Ejercicio 77 en la Sección 6.1 que\(\mbox{pH} = -\log[\mbox{H}^{+}]\) dónde\([\mbox{H}^{+}]\) está la concentración de iones hidrógeno en moles por litro. Requerimos\(7.8 \leq -\log[\mbox{H}^{+}] \leq 8.5\) o\(-7.8 \geq \log[\mbox{H}^{+}] \geq -8.5\). Para resolver esta desigualdad compuesta resolvemos\(-7.8 \geq \log[\mbox{H}^{+}]\)\(\log[\mbox{H}^{+}] \geq -8.5\) y tomamos la intersección de los conjuntos de soluciones. ³ La primera desigualdad rinde\(0 < [\mbox{H}^{+}] \leq 10^{-7.8}\) y la segunda rendimientos\([\mbox{H}^{+}] \geq 10^{-8.5}\). Tomar la intersección nos da nuestra respuesta final\(10^{-8.5} \leq [\mbox{H}^{+}] \leq 10^{-7.8}\). (Su profesor de Química puede querer que la respuesta esté escrita como\(3.16 \times 10^{-9} \leq [\mbox{H}^{+}] \leq 1.58 \times 10^{-8}\).) Después de ajustar cuidadosamente la ventana de visualización en la calculadora gráfica vemos que la gráfica de\(f(x) = -\log(x)\) se encuentra entre las líneas\(y = 7.8\) y\(y = 8.5\) en el intervalo\([3.16 \times 10^{-9}, 1.58 \times 10^{-8}]\).

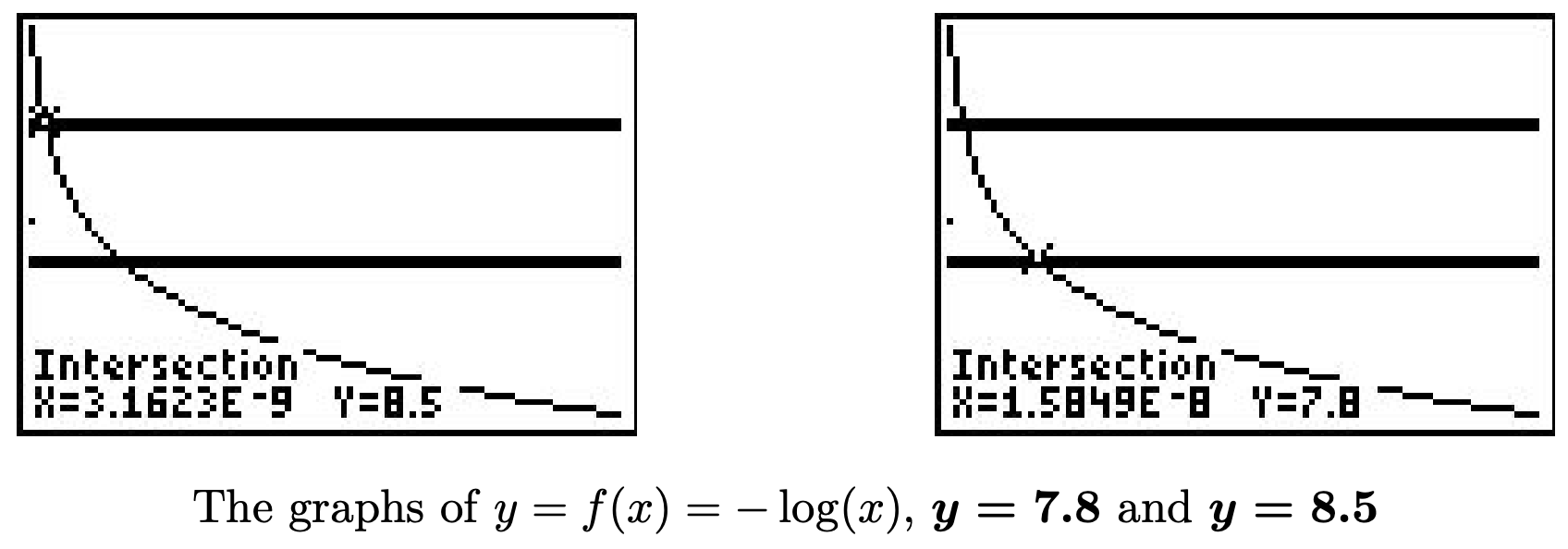
Las gráficas de\(y = f(x) = -\log(x)\),\(y = 7.8\) y\(y = 8.5\)

Cerramos esta sección encontrando una inversa de una función uno a uno que involucra logaritmos.

Ejemplo 6.4.4

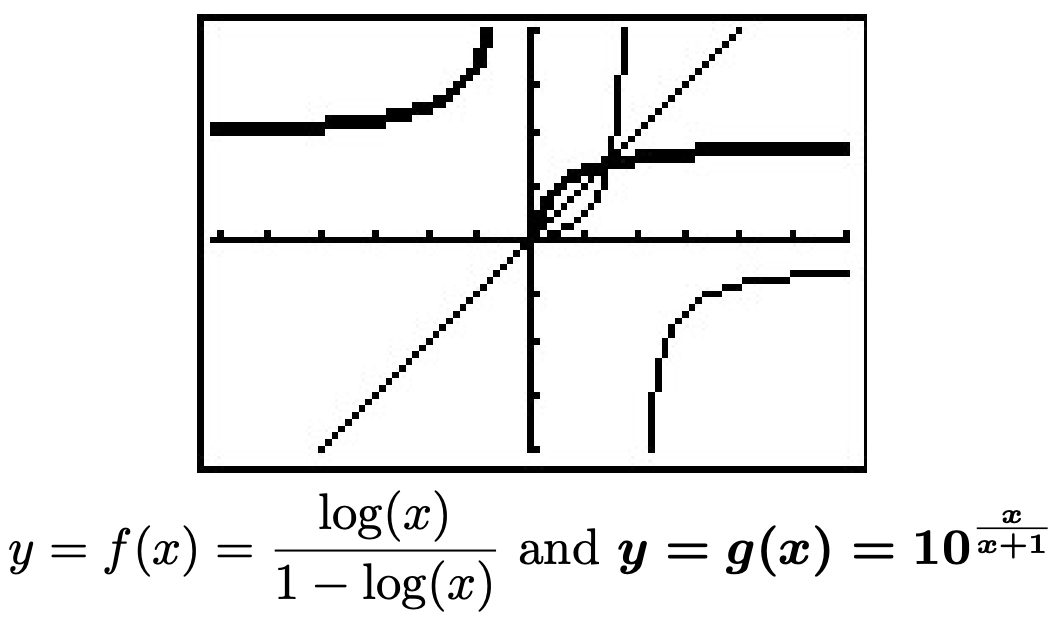
La función\(f(x) = \dfrac{\log(x)}{1-\log(x)}\) es uno a uno. Encuentre una fórmula para\(f^{-1}(x)\) y verifique su respuesta gráficamente usando su calculadora.

Solución

Primero escribimos\(y=f(x)\) luego intercambiamos el\(x\) y\(y\) y resolvemos para\(y\).

\[\begin{array}{rclr} y & = & f(x) & \\ y & = & \dfrac{\log(x)}{1-\log(x)} & \\[8pt] x & = & \dfrac{\log(y)}{1-\log(y)} & \mbox{Interchange $x$ and $y$.}\\[8pt] x\left(1-\log(y)\right) & = & \log(y) & \\ x - x\log(y) & = & \log(y) & \\ x & = & x \log(y) + \log(y) & \\ x & = & (x+1) \log(y) & \\ \dfrac{x}{x+1} & = & \log(y) & \\ y & = & 10^{\frac{x}{x+1}} & \mbox{Rewrite as an exponential equation.}\\ \end{array}\nonumber\]

Tenemos\(f^{-1}(x) = 10^{\frac{x}{x+1}}\). Graficar\(f\) y\(f^{-1}\) en la misma ventana de visualización rendimientos

6.4.1. Ejercicios

En los Ejercicios 1 - 24, resuelve la ecuación analíticamente.

1. \(\log(3x-1) = \log(4-x)\)
2. \(\log_{2}\left(x^{3}\right) = \log_{2}(x)\)
3. \(\ln\left(8-x^2\right)=\ln(2-x)\)
4. \(\log_{5}\left(18-x^2\right) = \log_{5}(6-x)\)
5. \(\log_{3}(7-2x) = 2\)
6. \(\log_{\frac{1}{2}} (2x-1) = -3\)
7. \(\ln\left(x^2-99\right) = 0\)
8. \(\log(x^2-3x) = 1\)
9. \(\log_{125} \left(\dfrac{3x-2}{2x+3}\right)=\dfrac{1}{3}\)
10. \(\log\left(\dfrac{x}{10^{-3}}\right) = 4.7\)
11. \(-\log(x) = 5.4\)[SixFourphequ]
12. \(10\log\left(\dfrac{x}{10^{-12}}\right) = 150\)
13. \(6-3\log_{5}(2x)=0\)
14. \(3\ln(x)-2=1-\ln(x)\)
15. \(\log_{3}(x - 4) + \log_{3}(x + 4) = 2\)
16. \(\log_{5}(2x + 1) + \log_{5}(x + 2) = 1\)
17. \(\log_{169}(3x + 7) - \log_{169}(5x - 9) = \dfrac{1}{2}\)
18. \(\ln(x+1) - \ln(x) = 3\)
19. \(2\log_{7}(x) = \log_{7}(2) + \log_{7}(x+12)\)
20. \(\log(x) - \log(2) = \log(x+8) - \log(x+2)\)
21. \(\log_{3}(x) = \log_{\frac{1}{3}}(x) + 8\)
22. \(\ln(\ln(x)) = 3\)
23. \(\left(\log(x)\right)^2=2\log(x)+15\)
24. \(\ln(x^{2}) = (\ln(x))^{2}\)

En los Ejercicios 25 - 30, resolver la desigualdad analíticamente.

25. \(\dfrac{1 - \ln(x)}{x^{2}} < 0\)
26. \(x\ln(x) - x > 0\)
27. \(10\log\left(\dfrac{x}{10^{-12}}\right) \geq 90\)
28. \(5.6 \leq \log\left(\dfrac{x}{10^{-3}}\right) \leq 7.1\)
29. \(2.3 < -\log(x) < 5.4\)
30. \(\ln(x^{2}) \leq (\ln(x))^{2}\)

En Ejercicios 31 - 34, usa tu calculadora para ayudarte a resolver la ecuación o desigualdad.

31. \(\ln(x) = e^{-x}\)
32. \(\ln(x) = \sqrt[4]{x}\)
33. \(\ln(x^{2} + 1) \geq 5\)
34. \(\ln(-2x^{3} - x^{2} + 13x - 6) < 0\)
35. Ya que\(f(x) = e^{x}\) es una función estrictamente creciente, si\(a < b\) entonces\(e^{a} < e^{b}\). Usa este hecho para resolver la desigualdad\(\ln(2x + 1) < 3\) sin un diagrama de signos. Utiliza esta técnica para resolver las desigualdades en los Ejercicios 27 - 29. (Compárelo con el Ejercicio 46 en la Sección 6.3.)
36. Resolver\(\ln(3 - y) - \ln(y) = 2x + \ln(5)\) para\(y\).
37. En el Ejemplo 6.4.4 encontramos la inversa\(f(x) = \dfrac{\log(x)}{1-\log(x)}\) de ser\(f^{-1}(x) = 10^{\frac{x}{x+1}}\).
    1. Demostrar eso\(\left(f^{-1} \circ f\right)(x) = x\) para todos\(x\) en el dominio de\(f\) y eso\(\left(f \circ f^{-1}\right)(x) = x\) para todos\(x\) en el dominio de\(f^{-1}\).
    2. Encuentra el rango de\(f\) encontrando el dominio de\(f^{-1}\).

    3. Dejar\(g(x) = \dfrac{x}{1 - x}\) y\(h(x) = \log(x)\). Demuestre eso\(f = g \circ h\) y\((g \circ h)^{-1} = h^{-1} \circ g^{-1}\).
       (Sabemos que esto es cierto en general por el Ejercicio 31 en la Sección 5.2, pero es agradable ver un ejemplo específico de la propiedad.)

38. Vamos\(f(x) = \dfrac{1}{2}\ln\left(\dfrac{1 + x}{1 - x}\right)\). Calcular\(f^{-1}(x)\) y encontrar su dominio y alcance.
39. Explicar la ecuación en el Ejercicio 10 y la desigualdad en el Ejercicio 28 anterior en términos de la escala de Richter para magnitud sísmica. (Ver Ejercicio 75 en la Sección 6.1.)
40. Explicar la ecuación en el Ejercicio 12 y la desigualdad en el Ejercicio 27 anterior en términos del nivel de intensidad sonora medido en decibelios. (Ver Ejercicio 76 en la Sección 6.1.)
41. Explicar la ecuación en el Ejercicio 11 y la desigualdad en el Ejercicio 29 anterior en términos del pH de una solución. (Ver Ejercicio 77 en la Sección 6.1.)
42. Con la ayuda de tus compañeros, resuelve la desigualdad\(\sqrt[n]{x} > \ln(x)\) para una variedad de números naturales\(n\). ¿Qué podría conjeturar sobre la “velocidad” a la que\(f(x) = \ln(x)\) crece frente a cualquier función\(n^{\textrm{th}}\) raíz principal?

6.4.2 Respuestas

1. \(x = \frac{5}{4}\)
2. \(x = 1\)
3. \(x=-2\)
4. \(x=-3,\, 4\)
5. \(x=-1\)
6. \(x=\frac{9}{2}\)
7. \(x=\pm 10\)
8. \(x=-2,\, 5\)
9. \(x = -\frac{17}{7}\)
10. \(x = 10^{1.7}\)
11. \(x = 10^{-5.4}\)
12. \(x = 10^{3}\)
13. \(x=\frac{25}{2}\)
14. \(x=e^{3/4}\)
15. \(x = 5\)
16. \(x = \frac{1}{2}\)
17. \(x = 2\)
18. \(x = \frac{1}{e^3-1}\)
19. \(x=6\)
20. \(x=4\)
21. \(x = 81\)
22. \(x = e^{e^3}\)
23. \(x=10^{-3}, \, 10^{5}\)
24. \(x = 1, \, x = e^{2}\)
25. \((e, \infty)\)
26. \((e, \infty)\)
27. \(\left[10^{-3}, \infty \right)\)
28. \(\left[10^{2.6}, 10^{4.1}\right]\)
29. \(\left(10^{-5.4}, 10^{-2.3}\right)\)
30. \((0, 1] \cup [e^{2}, \infty)\)
31. \(x \approx 1.3098\)
32. \(x \approx 4.177, \, x \approx 5503.665\)
33. \(\approx (-\infty, -12.1414) \cup (12.1414, \infty)\)
34. \(\approx (-3.0281, -3) \cup (0.5, 0.5991) \cup (1.9299, 2)\)
35. \(-\dfrac{1}{2} < x < \dfrac{e^{3} - 1}{2}\)
36. \(y = \dfrac{3}{5e^{2x} + 1}\)

38. \(f^{-1}(x) = \dfrac{e^{2x} - 1}{e^{2x} + 1} = \dfrac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\). (Para ver por qué reescribimos esto en este formulario, consulte el Ejercicio 51 en la Sección 11.10.) El dominio de\(f^{-1}\) es\((-\infty, \infty)\) y su rango es el mismo que el dominio de\(f\), es decir\((-1, 1)\).

---

Referencia

¹ Sin embargo, representan la misma familia de números complejos. Nos detenemos en este punto y remitimos al lector a un buen curso en Variables Complejas.

² Recordemos que una solución extraña es una respuesta obtenida analíticamente que no satisface la ecuación original.

³ Consulte la página 4 para una discusión de lo que esto significa.