10.3: Las Seis Funciones Circulares e Identidades Fundamentales

En la sección 10.2, definimos\(\cos(\theta)\) y\(\sin(\theta)\) para ángulos\(\theta\) usando los valores de coordenadas de puntos en el Círculo de Unidad. Como tal, estas funciones ganan el nombre de funciones circulares. ¹ Resulta que el coseno y el seno son solo dos de las seis funciones circulares de uso común que definimos a continuación.

Definición 10.2. Las funciones circulares

Supongamos que\(\theta\) es un ángulo trazado en posición estándar y\(P(x,y)\) es el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo de Unidad.

• El coseno de\(\theta\), denotado\(\cos(\theta)\), se define por\(\cos(\theta) = x\).
• El seno de\(\theta\), denotado\(\sin(\theta)\), se define por\(\sin(\theta) = y\).
• La secante de\(\theta\), denotada\(\sec(\theta)\), se define por\(\sec(\theta) = \dfrac{1}{x}\), proporcionada\(x \neq 0\).
• El cosecante de\(\theta\), denotado\(\csc(\theta)\), se define por\(\csc(\theta) = \dfrac{1}{y}\), proporcionado\(y \neq 0\).
• La tangente de\(\theta\), denotada\(\tan(\theta)\), se define por\(\tan(\theta) = \dfrac{y}{x}\), proporcionada\(x \neq 0\).
• La cotangente de\(\theta\), denotada\(\cot(\theta)\), se define por\(\cot(\theta) = \dfrac{x}{y}\), proporcionada\(y \neq 0\).

Si bien dejamos la historia del nombre 'sine' como un interesante proyecto de investigación en la sección 10.2, los nombres 'tangente' y 'secante' se pueden explicar usando el diagrama a continuación. Considera el ángulo agudo\(\theta\) abajo en posición estándar. Dejar\(P(x,y)\) denotar, como de costumbre, el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo de Unidad y dejar\(Q(1,y')\) denotar el punto en el lado terminal del\(\theta\) cual se encuentra en la línea vertical\(x=1\).

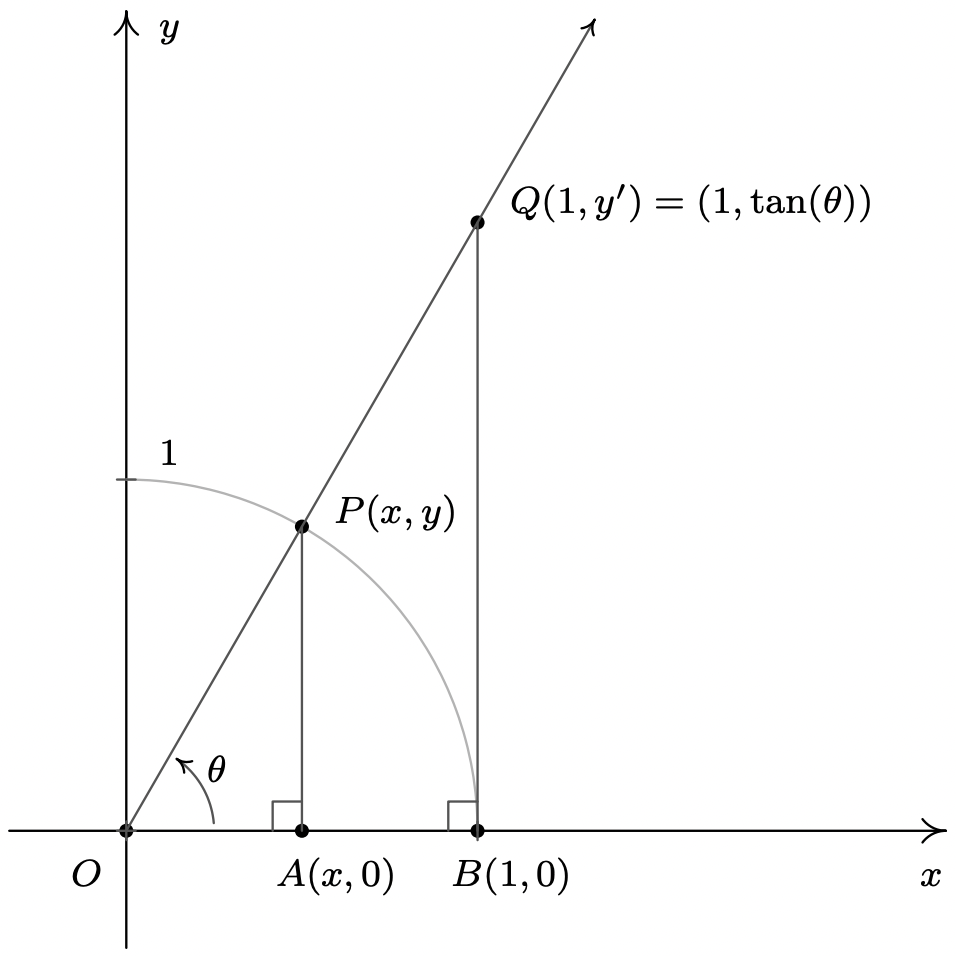
La palabra 'tangente' proviene del latín que significa 'tocar', y por esta razón, la línea\(x=1\) se denomina línea tangente al Círculo de Unidad ya que cruza, o 'toca', el círculo en un solo punto, a saber\((1,0)\). Dejar caer perpendiculares desde\(P\) y\(Q\) crea un par de triángulos similares\(\Delta OPA\) y\(\Delta OQB\). Así lo\(\frac{y'}{y} = \frac{1}{x}\) que da\(y' = \frac{y}{x} = \tan(\theta)\), donde esta última igualdad viene de aplicar la Definición 10.2. Acabamos de demostrar que para los ángulos agudos\(\theta\),\(\tan(\theta)\) es la\(y\) coordenada -coordenada del punto en el lado terminal del\(\theta\) cual se encuentra en la línea\(x = 1\) que es tangente al Círculo de Unidad. Ahora la palabra 'secante' significa 'cortar', así que una línea secante es cualquier línea que 'corta a través de' un círculo en dos puntos. ² La línea que contiene el lado terminal de\(\theta\) es una línea secante ya que cruza el Círculo Unitario en los Cuadrantes I y III. Con el punto\(P\) acostado en el Círculo Unitario, la longitud de la hipotenusa de\(\Delta OPA\) es\(1\). Si dejamos\(h\) denotar la longitud de la hipotenusa de\(\Delta OQB\), tenemos de triángulos similares que\(\frac{h}{1} = \frac{1}{x}\), o\(h = \frac{1}{x} = \sec(\theta)\). Por lo tanto\(\theta\), para un ángulo agudo,\(\sec(\theta)\) es la longitud del segmento de línea que se encuentra en la línea secante determinada por el lado terminal de\(\theta\) y “corta” la línea tangente\(x=1\). Estas observaciones no solo ayudan a explicar los nombres de estas funciones, sino que sirven de base para una desigualdad fundamental necesaria para el Cálculo que exploraremos en los Ejercicios.

De las seis funciones circulares, solo se definen coseno y seno para todos los ángulos. Desde\(\cos(\theta) = x\) y\(\sin(\theta) = y\) en la Definición 10.2, se acostumbra reformular las cuatro funciones circulares restantes en términos de coseno y seno. El siguiente teorema es el resultado de simplemente reemplazar\(x\) con\(\cos(\theta)\) y\(y\) con\(\sin(\theta)\) en la Definición 10.2.

Teorema 10.6. Identidades recíprocas y cocientes

• \(\sec(\theta) = \dfrac{1}{\cos(\theta)}\), siempre\(\cos(\theta) \neq 0\); si\(\cos(\theta) = 0\), no\(\sec(\theta)\) está definido.
• \(\csc(\theta) = \dfrac{1}{\sin(\theta)}\), siempre\(\sin(\theta) \neq 0\); si\(\sin(\theta) = 0\), no\(\csc(\theta)\) está definido.
• \(\tan(\theta) = \dfrac{\sin(\theta)}{\cos(\theta)}\), siempre\(\cos(\theta) \neq 0\); si\(\cos(\theta) = 0\), no\(\tan(\theta)\) está definido.
• \(\cot(\theta) = \dfrac{\cos(\theta)}{\sin(\theta)}\), siempre\(\sin(\theta) \neq 0\); si\(\sin(\theta) = 0\), no\(\cot(\theta)\) está definido.

Ya es hora de que se dé un ejemplo.

Ejemplo 10.3.1

Encuentra el valor indicado, si existe.

1. \(\sec\left(60^{\circ}\right)\)
2. \(\csc\left(\frac{7 \pi}{4} \right)\)
3. \(\cot(3)\)
4. \(\tan\left(\theta\right)\), donde\(\theta\) está cualquier ángulo coterminal con\(\frac{3\pi}{2}\).
5. \(\cos\left(\theta\right)\), donde\(\csc(\theta) = -\sqrt{5}\) y\(\theta\) es un ángulo del Cuadrante IV.
6. \(\sin\left(\theta\right)\), donde\(\tan(\theta) = 3\) y\(\pi < \theta < \frac{3\pi}{2}\).

Solución

1. Según el Teorema 10.6,\(\sec\left(60^{\circ}\right) = \frac{1}{\cos\left(60^{\circ}\right)}\). De ahí,\(\sec\left(60^{\circ}\right) = \frac{1}{(1/2)} = 2\).
2. Ya que\(\sin\left( \frac{7\pi}{4}\right) = - \frac{\sqrt{2}}{2}\),\(\csc\left( \frac{7\pi}{4}\right) = \frac{1}{\sin\left( \frac{7\pi}{4}\right)} = \frac{1}{- \sqrt{2}/2} = - \frac{2}{\sqrt{2}} = - \sqrt{2}\).
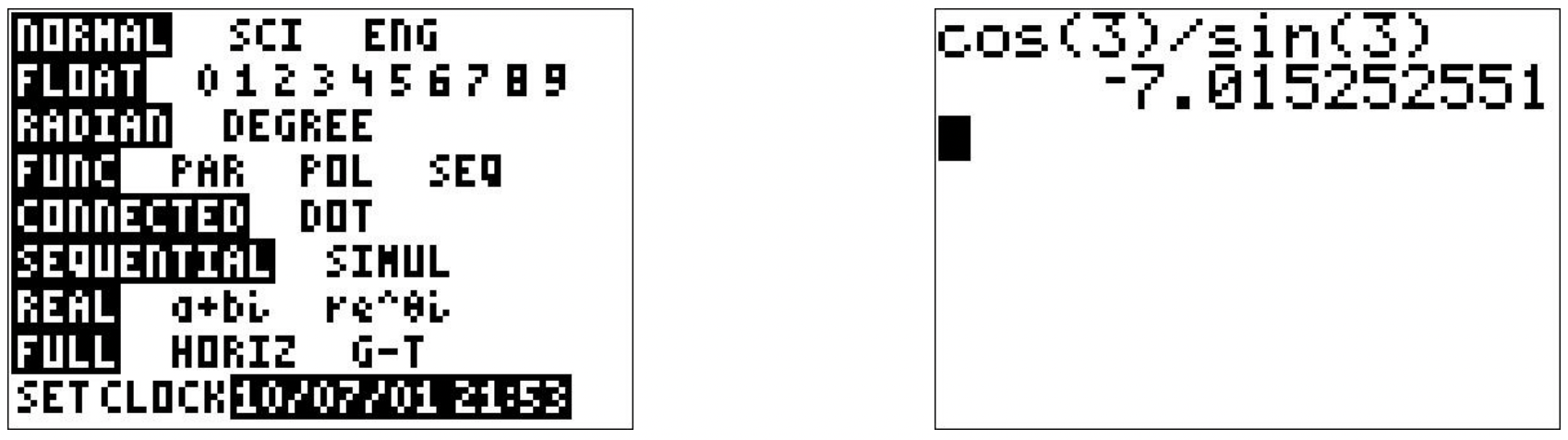
3. Dado que\(\theta = 3\) los radianes no son uno de los 'ángulos comunes' de la Sección 10.2, recurrimos a la calculadora para una aproximación decimal. Asegurando que la calculadora esté en modo radián, encontramos\(\cot(3) = \frac{\cos(3)}{\sin(3)} \approx -7.015\).

   

4. Si\(\theta\) es coterminal con\(\frac{3 \pi}{2}\), entonces\(\cos(\theta) = \cos\left(\frac{3 \pi}{2}\right) = 0\) y\(\sin(\theta) = \sin\left(\frac{3 \pi}{2}\right) = -1\). Intentar calcular\(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\) los resultados en\(\frac{-1}{0}\), así\(\tan(\theta)\) es indefinido.
5. Se nos da eso\(\csc(\theta) = \frac{1}{\sin(\theta)} = -\sqrt{5}\) así\(\sin(\theta) = -\frac{1}{\sqrt{5}} = -\frac{\sqrt{5}}{5}\). Como vimos en la Sección 10.2, podemos usar la Identidad Pitagórica\(\cos^{2}(\theta) + \sin^2(\theta) = 1\),, para encontrar\(\cos(\theta)\) conociendo\(\sin(\theta)\). Sustituyendo, obtenemos\(\cos^{2}(\theta) + \left(-\frac{\sqrt{5}}{5}\right)^2 = 1\), que da\(\cos^{2}(\theta) = \frac{4}{5}\), o\(\cos(\theta) = \pm \frac{2 \sqrt{5}}{5}\). Ya que\(\theta\) es un ángulo Cuadrante IV,\(\cos(\theta) > 0\), entonces\(\cos(\theta) = \frac{2 \sqrt{5}}{5}\).
6. Si\(\tan(\theta) = 3\), entonces\(\frac{\sin(\theta)}{\cos(\theta)} = 3\). Ten cuidado - esto NO significa que podamos tomar\(\sin(\theta) = 3\) y\(\cos(\theta) = 1\). En cambio, de\(\frac{\sin(\theta)}{\cos(\theta)} = 3\) obtenemos:\(\sin(\theta) = 3 \cos(\theta)\). Para relacionar\(\cos(\theta)\) y\(\sin(\theta)\), una vez más empleamos la Identidad Pitagórica,\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\). Resolviendo\(\sin(\theta) = 3 \cos(\theta)\) para\(\cos(\theta)\), encontramos\(\cos(\theta) = \frac{1}{3} \sin(\theta)\). Sustituyendo esto en la Identidad Pitagórica, encontramos\(\sin^{2}(\theta) + \left(\frac{1}{3} \sin(\theta)\right)^2 = 1\). Resolviendo,\(\sin^{2}(\theta) = \frac{9}{10}\) así lo conseguimos\(\sin(\theta) = \pm \frac{3 \sqrt{10}}{10}\). Ya que\(\pi < \theta < \frac{3\pi}{2}\),\(\theta\) es un ángulo Cuadrante III. Esto significa\(\sin(\theta) < 0\), entonces nuestra respuesta final es\(\sin(\theta) = - \frac{3 \sqrt{10}}{10}\).

Si bien las Identidades Recíprocas y Cocientes presentadas en el Teorema 10.6 nos permiten reducir siempre los problemas que involucran secante, cosecante, tangente y cotangente a problemas que involucran coseno y seno, no siempre es conveniente hacerlo. ³ Vale la pena tomarse el tiempo para memorizar los valores tangentes y cotangentes de los ángulos comunes que se resumen a continuación.

Valores tangentes y cotangentes de ángulos comunes

\ [\ begin {array} {|c|c||c|c|}
\ hline\ theta\ text {(grados)} &\ theta\ text {(radianes)} &\ tan (\ theta) &\ cot (\ theta)\
\ hline 0^ {\ circ} & 0 & 0 &\ text {undefined}\\
\ hline 30^ {\ circ} &\ frac {\ pi} {6} &\ frac {\ sqrt {3}} {3} & \ sqrt {3}\
\ hline 45^ {\ circ} &\ frac {\ pi} {4} & 1 & 1\
\ hline 60^ {\ circ} &\ frac {\ pi} {3} &\ sqrt {3} &\ frac {\ sqrt {3}} {3}} {3}\
\ hline 90^ {\ circ} &\ frac {\ pi} {2} &\ texto {undefined} & 0\\
\ hline
\ end { matriz}\ nonumber\]

Teorema de Acoplamiento 10.6 con el Teorema del Ángulo de Referencia, Teorema 10.2, obtenemos lo siguiente.

Teorema 10.7. Teorema de Ángulo de Referencia Generalizado

Los valores de las funciones circulares de un ángulo, si existen, son los mismos, hasta un signo, de las funciones circulares correspondientes de su ángulo de referencia. Más específicamente, si\(\alpha\) es el ángulo de referencia para\(\theta\), entonces:\(\cos(\theta) = \pm \cos(\alpha)\),\(\sin(\theta) = \pm \sin(\alpha)\),\(\sec(\theta) = \pm \sec(\alpha)\),\(\csc(\theta) = \pm \csc(\alpha)\),\(\tan(\theta) = \pm \tan(\alpha)\) y\(\cot(\theta) = \pm \cot(\alpha)\). La elección del (\(\pm\)) depende del cuadrante en el que se\(\theta\) encuentre el lado terminal de.

Ponemos el Teorema 10.7 a buen uso en el siguiente ejemplo.

Ejemplo 10.3.2

1. \(\sec(\theta) =2\)
2. \(\tan(\theta) = \sqrt{3}\)
3. \(\cot(\theta) = -1\).

Solución

1. Para resolver\(\sec(\theta) = 2\), convertimos a cosenos y obtenemos\(\frac{1}{\cos(\theta)} = 2\) o\(\cos(\theta) = \frac{1}{2}\). Esta es exactamente la misma ecuación que resolvimos en el Ejemplo 10.2.5, número 1, así sabemos que la respuesta es:\(\theta = \frac{\pi}{3} + 2\pi k\) o\(\theta = \frac{5\pi}{3} + 2\pi k\) para enteros\(k\).
2. 
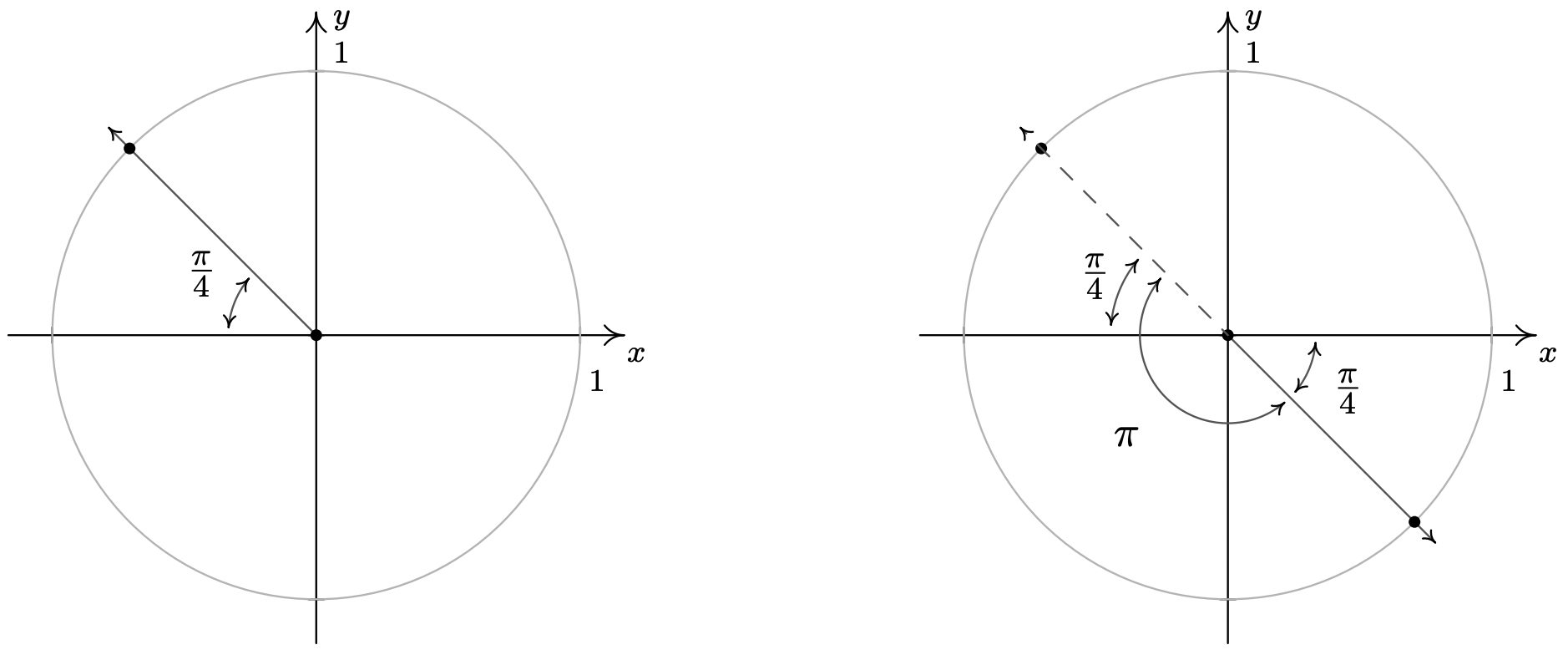
3. De la tabla de valores comunes, vemos que\(\frac{\pi}{4}\) tiene una cotangente de\(1\), lo que significa las soluciones para\(\cot(\theta) = -1\) tener un ángulo de referencia de\(\frac{\pi}{4}\). Para encontrar los cuadrantes en los que se encuentran nuestras soluciones, observamos que\(\cot(\theta) = \frac{x}{y}\) por un punto\((x,y)\) en el Círculo de Unidad donde\(y \neq 0\). Si\(\cot(\theta)\) es negativo, entonces\(x\) y\(y\) debe tener diferentes signos (es decir, uno positivo y otro negativo). De ahí que nuestras soluciones se encuentren en los Cuadrantes II y IV. Nuestra solución de Cuadrante II es\(\theta = \frac{3\pi}{4} + 2\pi k\), y para el Cuadrante IV, obtenemos\(\theta = \frac{7\pi}{4} + 2\pi k\) para enteros\(k\). ¿Se pueden combinar estas listas? Efectivamente pueden - una de esas formas de capturar todas las soluciones es:\(\theta = \frac{3\pi}{4} + \pi k\) para enteros\(k\).

   

Ya hemos visto la importancia de las identidades en la trigonometría. Nuestra siguiente tarea es utilizar las Identidades Recíprocas y Cocientes encontradas en el Teorema 10.6 junto con la Identidad Pitágoras que se encuentra en el Teorema 10.1 para derivar nuevas identidades similares a Pitagóreas para las cuatro funciones circulares restantes. Asumiendo\(\cos(\theta) \neq 0\), podemos comenzar con\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\) y dividir ambos lados por\(\cos^{2}(\theta)\) para obtener\(1 + \frac{\sin^{2}(\theta)}{\cos^{2}(\theta)} = \frac{1}{\cos^{2}(\theta)}\). Usando propiedades de exponentes junto con las identidades recíprocas y cocientes, esto se reduce a\(1 + \tan^{2}(\theta) = \sec^{2}(\theta)\). Si\(\sin(\theta) \neq 0\), podemos dividir ambos lados de la identidad\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\) por\(\sin^{2}(\theta)\), aplicar una vez más el Teorema 10.6, y obtener\(\cot^{2}(\theta) + 1 = \csc^{2}(\theta)\). Estas tres Identidades pitagóricas merecen ser memorizadas y ellas, junto con algunas de sus otras formas comunes, se resumen en el siguiente teorema.

Teorema 10.8. Las identidades pitagóricas

1. \(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\).

   Formas Alternativas Comunes:

   • \(1 - \sin^{2}(\theta) = \cos^{2}(\theta)\)
   • \(1 - \cos^{2}(\theta) = \sin^{2}(\theta)\)
2. \(1 + \tan^{2}(\theta) = \sec^{2}(\theta)\), siempre\(\cos(\theta) \neq 0\).

   Formas Alternativas Comunes:

   • \(\sec^{2}(\theta) - \tan^{2}(\theta) = 1\)
   • \(\sec^{2}(\theta) - 1 = \tan^{2}(\theta)\)
3. \(1 + \cot^{2}(\theta) = \csc^{2}(\theta)\), siempre\(\sin(\theta) \neq 0\).

   Formas Alternativas Comunes:

   • \(\csc^{2}(\theta) - \cot^{2}(\theta) = 1\)
   • \(\csc^{2}(\theta) - 1 = \cot^{2}(\theta)\)

Las identidades trigonométricas juegan un papel importante no solo en la trigonometría, sino también en el cálculo. Los usaremos en este libro para encontrar los valores de las funciones circulares de un ángulo y resolver ecuaciones y desigualdades. En Cálculo, son necesarios para simplificar expresiones que de otro modo serían complicadas. En el siguiente ejemplo, hacemos buen uso de los Teoremas 10.6 y 10.8.

Ejemplo 10.3.3.

Verificar las siguientes identidades. Supongamos que todas las cantidades están definidas.

1. \(\dfrac{1}{\csc(\theta)} = \sin(\theta)\)
2. \(\tan(\theta) = \sin(\theta) \sec(\theta)\)
3. \((\sec(\theta) - \tan(\theta)) (\sec(\theta) + \tan(\theta)) = 1\)
4. \(\dfrac{\sec(\theta)}{1 - \tan(\theta)} = \dfrac{1}{\cos(\theta) - \sin(\theta)}\)
5. \(6\sec(\theta) \tan(\theta) = \dfrac{3}{1-\sin(\theta)} - \dfrac{3}{1 + \sin(\theta)}\)
6. \(\dfrac{\sin(\theta)}{1 - \cos(\theta)} = \dfrac{1 + \cos(\theta)}{\sin(\theta)}\)

Solución

Al verificar identidades, normalmente comenzamos con el lado más complicado de la ecuación y usamos identidades conocidas para transformarla en el otro lado de la ecuación.

1. Para verificar\(\frac{1}{\csc(\theta)} = \sin(\theta)\), comenzamos por el lado izquierdo. Usando\(\csc(\theta) = \frac{1}{\sin(\theta)}\), obtenemos:\[\dfrac{1}{\csc(\theta)} = \dfrac{1}{\frac{1}{\sin(\theta)}} = \sin(\theta),\nonumber\]
2. Comenzando por el lado derecho de\(\tan(\theta) = \sin(\theta) \sec(\theta)\), usamos\(\sec(\theta) = \frac{1}{\cos(\theta)}\) y encontramos:\[\sin(\theta) \sec(\theta) = \sin(\theta) \dfrac{1}{\cos(\theta)} = \dfrac{\sin(\theta)}{\cos(\theta)} = \tan(\theta),\nonumber\]
3. Expandir el lado izquierdo de la ecuación da:\((\sec(\theta) - \tan(\theta)) (\sec(\theta) + \tan(\theta)) = \sec^{2}(\theta) - \tan^{2}(\theta)\). Según el Teorema 10.8,\(\sec^{2}(\theta) - \tan^{2}(\theta) = 1\). Poniéndolo todo junto,\[(\sec(\theta) - \tan(\theta)) (\sec(\theta) + \tan(\theta)) = \sec^{2}(\theta) - \tan^{2}(\theta) = 1.\nonumber\]
4. Si bien ambos lados de nuestra última identidad contienen fracciones, el lado izquierdo nos brinda más oportunidades para usar nuestras identidades. ⁵ Sustituyendo\(\sec(\theta) = \frac{1}{\cos(\theta)}\) y\(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\), obtenemos:

   \[\begin{array}{rcl} \dfrac{\sec(\theta)}{1 - \tan(\theta)} & = & \dfrac{ \dfrac{1}{\cos(\theta)}}{1 - \dfrac{\sin(\theta)}{\cos(\theta)}} = \dfrac{ \dfrac{1}{\cos(\theta)}}{1 - \dfrac{\sin(\theta)}{\cos(\theta)}} \cdot \dfrac{\cos(\theta)}{\cos(\theta)} \\ [.4in] & = & \dfrac{\left( \dfrac{1}{\cos(\theta)} \right) ( \cos(\theta) )}{\left(1 - \dfrac{\sin(\theta)}{\cos(\theta)}\right)(\cos(\theta))} = \dfrac{1}{(1)(\cos(\theta)) - \left(\dfrac{\sin(\theta)}{\cos(\theta)}\right)(\cos(\theta))} \\ [.4in] & = & \dfrac{1}{\cos(\theta) - \sin(\theta)}, \end{array}\nonumber\]que es exactamente lo que nos habíamos propuesto mostrar.

5. El lado derecho de la ecuación parece ser más prometedor. Obtenemos denominadores comunes y agregamos:

   \[\begin{array}{rcl} \dfrac{3}{1-\sin(\theta)} - \dfrac{3}{1 + \sin(\theta)} & = & \dfrac{3(1 + \sin(\theta))}{(1-\sin(\theta))(1 + \sin(\theta))} - \dfrac{3(1-\sin(\theta))}{(1 + \sin(\theta))(1-\sin(\theta))} \\[4pt] & = & \dfrac{3 + 3\sin(\theta)}{1 - \sin^{2}(\theta)} - \dfrac{3 - 3\sin(\theta)}{1 - \sin^{2}(\theta)} \\[4pt] & = & \dfrac{(3 + 3\sin(\theta)) - (3 - 3\sin(\theta))}{1 - \sin^{2}(\theta)} \\[4pt] & = & \dfrac{6 \sin(\theta)}{1 - \sin^{2}(\theta)} \end{array}\nonumber\]

   En este punto, vale la pena hacer una pausa para recordarnos nuestro objetivo. Deseamos transformar esta expresión en\(6\sec(\theta) \tan(\theta)\). Utilizando una identidad recíproca y cociente, encontramos\(6\sec(\theta) \tan(\theta) = 6 \left(\frac{1}{\cos(\theta)}\right) \left(\frac{\sin(\theta)}{\cos(\theta)}\right)\). En otras palabras, necesitamos conseguir cosenos en nuestro denominador. El teorema 10.8 nos dice\(1 - \sin^{2}(\theta) = \cos^{2}(\theta)\) así que obtenemos:

   \[\begin{array}{rcl} \dfrac{3}{1-\sin(\theta)} - \dfrac{3}{1 + \sin(\theta)} & = & \dfrac{6 \sin(\theta)}{1 - \sin^{2}(\theta)}= \dfrac{6 \sin(\theta)}{\cos^{2}(\theta)} \\[4pt] & = & 6 \left(\dfrac{1}{\cos(\theta)}\right)\left( \dfrac{\sin(\theta)}{\cos(\theta)}\right) = 6 \sec(\theta) \tan(\theta) \\ \end{array}\nonumber\]

6. Es discutible qué lado de la identidad es más complicado. Una cosa que destaca es que el denominador del lado izquierdo es\(1-\cos(\theta)\), mientras que el numerador del lado derecho lo es\(1+\cos(\theta)\). Esto sugiere la estrategia de comenzar por el lado izquierdo y multiplicar el numerador y denominador por la cantidad\(1+\cos(\theta)\):

   \[\begin{array}{rcl} \dfrac{\sin(\theta)}{1 - \cos(\theta)} & = & \dfrac{\sin(\theta)}{(1 - \cos(\theta))} \cdot \dfrac{(1 + \cos(\theta))}{(1 + \cos(\theta))} = \dfrac{\sin(\theta)(1 + \cos(\theta))}{(1 - \cos(\theta))(1 + \cos(\theta))} \\[4pt] & = & \dfrac{\sin(\theta)(1 + \cos(\theta))}{1 - \cos^{2}(\theta)} = \dfrac{\sin(\theta)(1 + \cos(\theta))}{\sin^{2}(\theta)} \\[4pt] & = & \dfrac{\cancel{\sin(\theta)}(1 + \cos(\theta))}{\cancel{\sin(\theta)}\sin(\theta)} = \dfrac{1 + \cos(\theta)}{\sin(\theta)} \end{array}\nonumber\]

En el Ejemplo 10.3.3 número 6 anterior, vemos que multiplicar\(1-\cos(\theta)\) por\(1+\cos(\theta)\) produce una diferencia de cuadrados que se puede simplificar a un término usando el Teorema 10.8. Este es exactamente el mismo tipo de fenómeno que ocurre cuando multiplicamos expresiones como\(1 - \sqrt{2}\) por\(1+\sqrt{2}\) o\(3 - 4i\) por\(3+4i\). (¿Puedes recordar instancias de Álgebra donde hicimos tales cosas?) Por esta razón, las cantidades\((1-\cos(\theta))\) y\((1+\cos(\theta))\) se llaman 'Conjugados Pitágoros'. A continuación se muestra una lista de otros conjugados pitagóricos comunes.

Conconjugados pitagóricos

• \(1 - \cos(\theta)\)y\(1+\cos(\theta)\):\((1-\cos(\theta))(1+\cos(\theta)) = 1 - \cos^{2}(\theta) = \sin^{2}(\theta)\)
• \(1-\sin(\theta)\)y\(1 + \sin(\theta)\):\((1-\sin(\theta))(1+\sin(\theta)) = 1 - \sin^{2}(\theta) = \cos^{2}(\theta)\)
• \(\sec(\theta)-1\)y\(\sec(\theta)+1\):\((\sec(\theta)-1)(\sec(\theta)+1) = \sec^{2}(\theta) - 1 = \tan^{2}(\theta)\)
• \(\sec(\theta)-\tan(\theta)\)y\(\sec(\theta)+\tan(\theta)\):\((\sec(\theta)-\tan(\theta))(\sec(\theta)+\tan(\theta)) = \sec^{2}(\theta) - \tan^{2}(\theta) = 1\)
• \(\csc(\theta)-1\)y\(\csc(\theta)+1\):\((\csc(\theta)-1)(\csc(\theta)+1) = \csc^{2}(\theta) - 1 = \cot^{2}(\theta)\)
• \(\csc(\theta)-\cot(\theta)\)y\(\csc(\theta)+\cot(\theta)\):\((\csc(\theta)-\cot(\theta))(\csc(\theta)+\cot(\theta)) = \csc^{2}(\theta) - \cot^{2}(\theta) = 1\)

Verificar identidades trigonométricas requiere una mezcla saludable de tenacidad e inspiración. Tendrás que pasar muchas horas luchando con ellos solo para dominar lo básico. Como muchas cosas en la vida, no hay atajo aquí — no hay un algoritmo completo para verificar identidades. Sin embargo, a continuación se proporciona un resumen de algunas estrategias que pueden ser útiles (dependiendo de la situación) y se proporciona una amplia práctica para usted en los Ejercicios.

Estrategias para verificar identidades

• Intenta trabajar en el lado más complicado de la identidad.
• Utilizar las Identidades Recíprocas y Cocientes en el Teorema 10.6 para escribir funciones en un lado de la identidad en términos de las funciones del otro lado de la identidad. Simplifique las fracciones complejas resultantes.
• Agregar expresiones racionales con denominadores diferentes mediante la obtención de denominadores comunes.
• Utilizar las Identidades Pitágoras en el Teorema 10.8 para 'intercambiar' senos y cosenos, secantes y tangentes, cosecantes y cotangentes, y simplificar sumas o diferencias de cuadrados a un término.
• Multiplicar numerador y denominador por Conconjugados de Pitágoras para aprovechar las Identidades Pitágoras en el Teorema 10.8.
• Si te encuentras atascado trabajando con un lado de la identidad, intenta comenzar por el otro lado de la identidad y mira si puedes encontrar la manera de puentear las dos partes de tu trabajo.

10.3.1. Más allá del círculo de unidades

En la Sección 10.2 generalizamos las funciones coseno y seno desde coordenadas en el Círculo de Unidad hasta coordenadas en círculos de radio\(r\). Usando el Teorema 10.3 en conjunto con el Teorema 10.8, generalizamos las funciones circulares restantes en especie.

Teorema 10.9.

Supongamos que\(Q(x,y)\) es el punto en el lado terminal de un ángulo\(\theta\) (trazado en posición estándar) que se encuentra en el círculo de radio\(r\),\(x^2+y^2 = r^2\). Entonces:

• \(\sec(\theta) = \dfrac{r}{x} = \dfrac{\sqrt{x^2+y^2}}{x}\), siempre\(x \neq 0\).
• \(\csc(\theta) = \dfrac{r}{y} = \dfrac{\sqrt{x^2+y^2}}{y}\), siempre\(y \neq 0\).
• \(\tan(\theta) = \dfrac{y}{x}\), siempre\(x \neq 0\).
• \(\cot(\theta) = \dfrac{x}{y}\), siempre\(y \neq 0\).

Ejemplo 10.3.4

1. Supongamos que el lado terminal de\(\theta\), cuando se traza en posición estándar, contiene el punto\(Q(3,-4)\). Encuentra los valores de las seis funciones circulares de\(\theta\).
2. Supongamos que\(\theta\) es un ángulo Cuadrante IV con\(\cot(\theta) = -4\). Encuentra los valores de las cinco funciones circulares restantes de\(\theta\).

Solución.

1. Desde\(x = 3\) y\(y=-4\),\(r = \sqrt{x^2 + y^2} = \sqrt{(3)^2+(-4)^2} = \sqrt{25} = 5\). El teorema 10.9 nos dice\(\cos(\theta) = \frac{3}{5}\)\(\sin(\theta) = -\frac{4}{5}\),\(\sec(\theta) = \frac{5}{3}\),\(\csc(\theta) = -\frac{5}{4}\),\(\tan(\theta) = -\frac{4}{3}\) y\(\cot(\theta) = - \frac{3}{4}\).
2. Para poder utilizar el Teorema 10.9, necesitamos encontrar un punto\(Q(x,y)\) que se encuentre en el lado terminal de\(\theta\), cuando\(\theta\) se traza en posición estándar. Eso tenemos\(\cot(\theta) = -4 = \frac{x}{y}\), y como\(\theta\) es un ángulo Cuadrante IV, también sabemos\(x>0\) y\(y< 0\). Viendo\(-4 = \frac{4}{-1}\), podemos elegir ⁶\(x = 4\) y\(y = -1\) para que\(r = \sqrt{x^2+y^2} = \sqrt{(4)^2 + (-1)^2} = \sqrt{17}\). Aplicando el Teorema 10.9 una vez más\(\cos(\theta) = \frac{4}{\sqrt{17}} = \frac{4 \sqrt{17}}{17}\), encontramos\(\sin(\theta) =- \frac{1}{\sqrt{17}} = -\frac{\sqrt{17}}{17}\),,\(\sec(\theta) = \frac{\sqrt{17}}{4}\),\(\csc(\theta) = - \sqrt{17}\) y\(\tan(\theta) = -\frac{1}{4}\).

También podemos especializarnos el Teorema 10.9 al caso de los ángulos agudos\(\theta\) que residen en un triángulo rectángulo, como se visualiza a continuación.

 

Teorema 10.10.

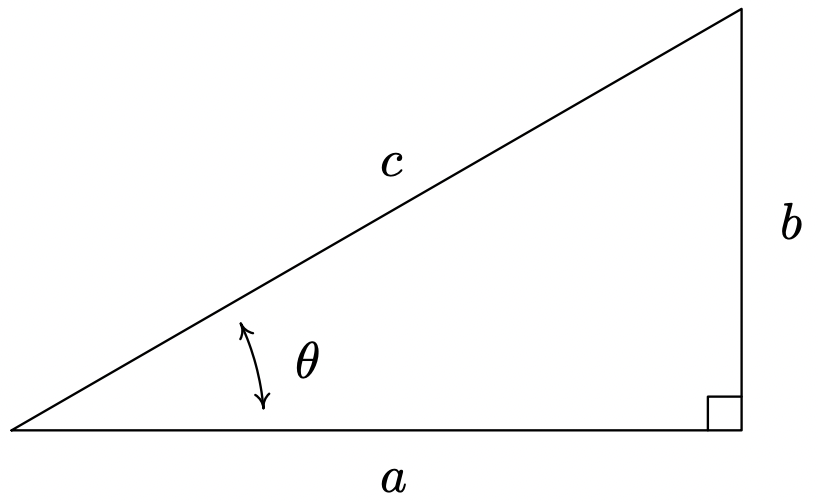
Supongamos que\(\theta\) es un ángulo agudo que reside en un triángulo rectángulo. Si la longitud del lado adyacente a\(\theta\) es\(a\), la longitud del lado opuesto\(\theta\) es\(b\), y la longitud de la hipotenusa es\(c\), entonces\[\begin{array}{llll} \tan(\theta) = \dfrac{b}{a} \;\;\;\;\;\; & \sec(\theta) = \dfrac{c}{a} \;\;\;\;\;\; & \csc(\theta) = \dfrac{c}{b} \;\;\;\;\;\; & \cot(\theta) = \dfrac{a}{b} \end{array}\nonumber\]

El siguiente ejemplo utiliza el Teorema 10.10 así como el concepto de un 'ángulo de inclinación'. El ángulo de inclinación (o ángulo de elevación) de un objeto se refiere al ángulo cuyo lado inicial es algún tipo de línea base (digamos, el suelo), y cuyo lado terminal es la línea de visión a un objeto por encima de la línea base. Esto se representa esquemáticamente a continuación.

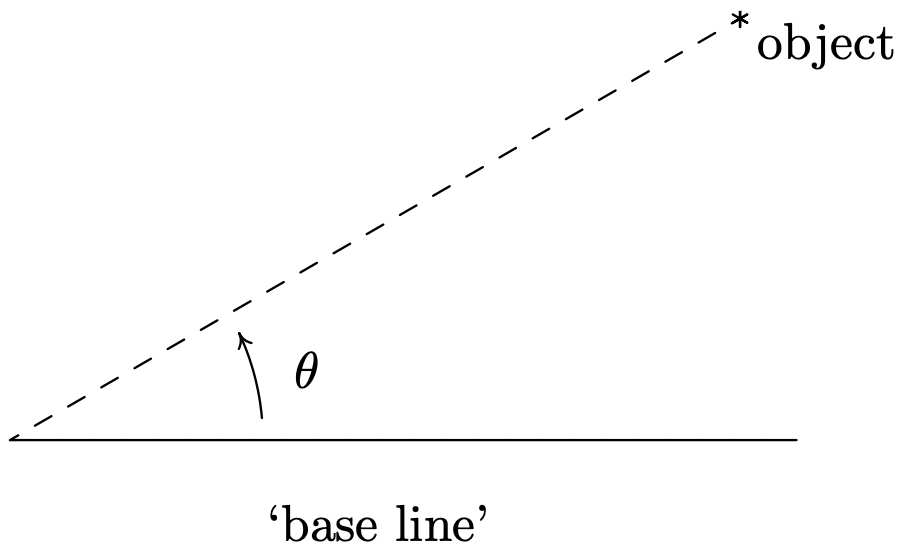El ángulo de inclinación desde la línea base hasta el objeto es θ

Ejemplo 10.3.5

1. El ángulo de inclinación desde un punto en el suelo a 30 pies de distancia hasta la cima de Lakeland Armington Clocktower ⁷ es\(60^{\circ}\). Encuentra la altura de la Torre del Reloj al pie más cercano.
2. Para determinar la altura de un árbol de secoya de California, se realizan dos avistamientos desde el suelo, uno a 200 pies directamente detrás del otro. Si los ángulos de inclinación eran\(45^{\circ}\) y\(30^{\circ}\), respectivamente, ¿qué tan alto es el árbol al pie más cercano?

Solución.

1. Podemos representar la situación del problema usando un triángulo rectángulo como se muestra a continuación. Si dejamos\(h\) denotar la altura de la torre, entonces el Teorema 10.10 da\(\tan\left(60^{\circ}\right) = \frac{h}{30}\). De esto obtenemos\(h = 30 \tan\left(60^{\circ}\right) = 30 \sqrt{3} \approx 51.96\). De ahí que la Torre del Reloj mide aproximadamente\(52\) pies de altura.

   Encontrar la altura de la Torre del Reloj

2. Dibujando la situación problemática a continuación, nos encontramos con dos incógnitas: la altura\(h\) del árbol y la distancia\(x\) desde la base del árbol hasta el primer punto de observación.

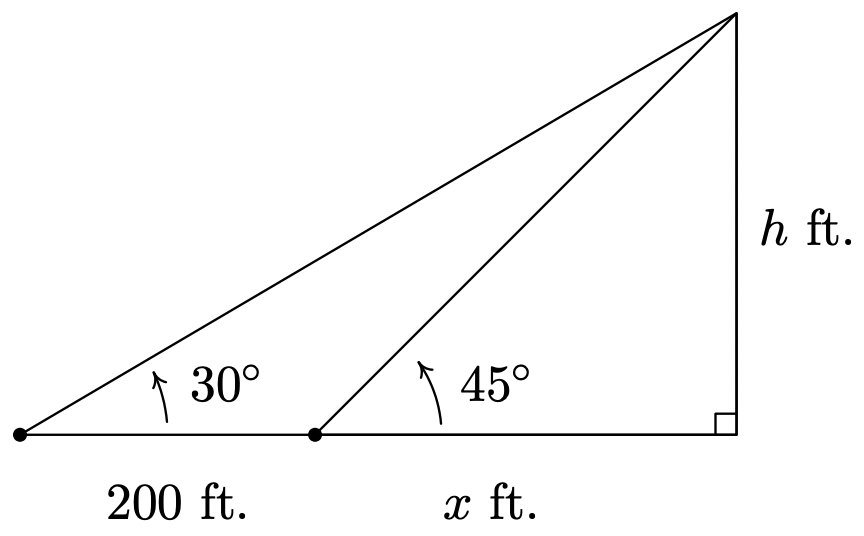   Encontrar la altura de una secoya de California

   Usando el Teorema 10.10, obtenemos un par de ecuaciones:\(\tan\left(45^{\circ}\right) = \frac{h}{x}\) y\(\tan\left(30^{\circ}\right) = \frac{h}{x+200}\). Ya que\(\tan\left(45^{\circ}\right) = 1\), la primera ecuación da\(\frac{h}{x} = 1\), o\(x = h\). Sustituir esto en la segunda ecuación da\(\frac{h}{h+200} = \tan\left(30^{\circ}\right) = \frac{\sqrt{3}}{3}\). Despejando fracciones, obtenemos\(3h = (h+200) \sqrt{3}\). El resultado es una ecuación lineal para\(h\), por lo que procedemos a expandir el lado derecho y reunir todos los términos que involucran\(h\) a un lado.

   \[\begin{array}{rcl} 3h & = & (h+200)\sqrt{3} \\[4pt] 3h & = & h \sqrt{3} + 200 \sqrt{3} \\[4pt] 3h - h \sqrt{3} & = & 200 \sqrt{3} \\[4pt] (3-\sqrt{3}) h & = & 200 \sqrt{3} \\[4pt] h & = & \dfrac{200\sqrt{3}}{3-\sqrt{3}} \approx 273.20 \\ \end{array}\nonumber\]

   De ahí que el árbol tenga aproximadamente\(273\) pies de altura.

Como hicimos en la Sección 10.2.1, podemos considerar las seis funciones circulares como funciones de números reales. En esta etapa, hay tres formas equivalentes de definir las funciones\(\sec(t)\),\(\csc(t)\),\(\tan(t)\) y\(\cot(t)\) para los números reales\(t\). Primero, podríamos pasar por la formalidad de la función de envoltura en la página 704 y definir estas funciones como las proporciones\(x\) y\(y\) coordenadas apropiadas de puntos en el Círculo de Unidad; en segundo lugar, podríamos definirlas asociando el número real\(t\) con los\(\theta = t\) radianes angulares de manera que el valor de la función trigonométrica de\(t\) coincide con el de\(\theta\); por último, podríamos simplemente definirlos utilizando las Identidades Recíprocas y Cocientes como combinaciones de las funciones\(f(t) = \cos(t)\) y\(g(t) = \sin(t)\). En la actualidad, adoptamos el último enfoque. Ahora nos propusimos determinar los dominios y rangos de las cuatro funciones circulares restantes. Considerar la función\(F(t) = \sec(t)\) definida como\(F(t) = \sec(t) = \frac{1}{\cos(t)}\). Sabemos que\(F\) es indefinido cuando sea\(\cos(t) = 0\). Del Ejemplo 10.2.5 número 3, sabemos\(\cos(t) = 0\) cuándo\(t = \frac{\pi}{2} + \pi k\) para enteros\(k\). De ahí que nuestro dominio para\(F(t) = \sec(t)\), en conjunto la notación constructor es\(\left\{t: t \neq \frac{\pi}{2}+\pi k, \text { for integers } k\right\}\). Para entender mejor con qué conjunto de números reales estamos tratando, vale la pena escribir y graficar este conjunto. Corriendo a través de algunos valores de\(k\), encontramos que el dominio es\(\{ t : t \neq \pm \frac{\pi}{2}, \, \pm \frac{3\pi}{2}, \, \pm \frac{5\pi}{2}, \, \ldots \}\). Graficando este conjunto en la línea numérica que obtenemos

 

Usando la notación de intervalos para describir este conjunto, obtenemos\[\ldots \cup \left( -\frac{5\pi}{2}, -\frac{3\pi}{2}\right) \cup \left( -\frac{3\pi}{2}, -\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \frac{3\pi}{2}\right) \cup \left(\frac{3\pi}{2}, \frac{5\pi}{2}\right) \cup \ldots\nonumber\]

¡Esto es engorroso, por decir lo menos! Para escribir esto de una manera más compacta, observamos que a partir de la descripción set-builder del dominio, el punto\(k\) th excluido del dominio, al que llamaremos\(x_{k}\), se puede encontrar por la fórmula\(x_{k} = \frac{\pi}{2} + \pi k\). (Estamos usando notación de secuencia del Capítulo 9.) Obteniendo un denominador común y factorizando el\(\pi\) en el numerador, obtenemos\(x_{k} = \frac{(2k+1)\pi}{2}\). El dominio consiste en los intervalos determinados por puntos sucesivos\(x_{k}\):\(\left(x_{k}, x_{k+1}\right) = \left( \frac{(2k+1)\pi}{2}, \frac{(2k+3)\pi}{2}\right)\). Para poder capturar todos los intervalos en el dominio, se\(k\) deben recorrer todos los enteros, es decir,,\(k = 0\),\(\pm 1\),\(\pm 2\),... La forma en que denotamos tomar la unión de infinitamente muchos intervalos como este es usar lo que llamamos en este texto notación de intervalo extendido. El dominio de ahora se\(F(t) = \sec(t)\) puede escribir como

\[\bigcup_{k = -\infty}^{\infty} \left( \frac{(2k+1)\pi}{2}, \frac{(2k+3) \pi}{2} \right)\nonumber\]

El lector debe comparar esta notación con la notación de suma introducida en la Sección 9.2, en particular la notación utilizada para describir series geométricas en el Teorema 9.2. De la misma manera el índice\(k\) de la serie nunca\[\displaystyle{\sum_{k = 1}^{\infty} a r^{k-1}}\nonumber\] puede igualar el límite superior\(\infty\), sino que abarca todos los números naturales, el índice\(k\) en la unión nunca\[\displaystyle{\bigcup_{k = -\infty}^{\infty} \left( \frac{(2k+1)\pi}{2}, \frac{(2k+3) \pi}{2} \right)}\nonumber\] puede ser realmente\(\infty\) o\(-\infty\), sino más bien, esto transmite la idea de que\(k\) se extiende a través de todos los números enteros. Ahora que hemos determinado minuciosamente el dominio de\(F(t) = \sec(t)\), es el momento de discutir el rango. Una vez más, apelamos a la definición\(F(t) = \sec(t) = \frac{1}{\cos(t)}\). El rango de\(f(t) = \cos(t)\) es\([-1,1]\), y desde no\(F(t) = \sec(t)\) está definido cuándo\(\cos(t) = 0\), dividimos nuestra discusión en dos casos: cuándo\(0 < \cos(t) \leq 1\) y cuándo\(-1 \leq \cos(t) < 0\). Si\(0 < \cos(t) \leq 1\), entonces podemos dividir la desigualdad\(\cos(t) \leq 1\) por\(\cos(t)\) para obtener\(\sec(t) = \frac{1}{\cos(t)} \geq 1\). Además, utilizando la notación introducida en la Sección 4.2, tenemos que como\(\cos(t) \rightarrow 0^{+}\),\(\sec (t)=\frac{1}{\cos (t)} \approx \frac{1}{\text { very small (+) }} \approx \text { very big }(+)\). En otras palabras, como\(\cos(t) \rightarrow 0^{+}, \sec(t) \rightarrow \infty\). Si, por otro lado, si\(-1 \leq \cos(t) < 0\), entonces dividir por\(\cos(t)\) provoca una reversión de la desigualdad para que eso\(\sec(t) = \frac{1}{\sec(t)} \leq -1\). En este caso, como\(\cos(t) \rightarrow 0^{-}\)\(\sec (t)=\frac{1}{\cos (t)} \approx \frac{1}{\text { very small }(-)} \approx \text { very big }(-)\), para que como\(\cos (t) \rightarrow 0^{-}\), obtengamos\(\sec(t) \rightarrow -\infty\). Ya\(f(t) = \cos(t)\) que admite todos los valores en\([-1,1]\), la función\(F(t) = \sec(t)\) admite todos los valores en\((-\infty, -1] \cup [1,\infty)\). Usando la notación set-builder, el rango de se\(F(t) = \sec(t)\) puede escribir como\(\{u: u \leq-1 \text { or } u \geq 1\}\), o, más sucintamente, ⁸ como\(\{ u :|u| \geq 1 \}\). ⁹ Se pueden usar argumentos similares para determinar los dominios y rangos de las tres funciones circulares restantes:\(\csc(t)\),\(\tan(t)\) y\(\cot(t)\). Se anima al lector a hacerlo. (Ver los Ejercicios.) Por ahora, reunimos estos hechos en el teorema a continuación.

Teorema 10.11. Dominios y rangos de las funciones circulares

• La función\(f(t) = cos(t)\)
  • — tiene dominio (−∞, ∞)
  • tiene rango [−1, 1]
• La función\(g(t) = sin(t)\)
  • tiene dominio (−∞, ∞)
  • tiene rango [−1, 1]
• La función\(F(t) = \sec(t) = \dfrac{1}{\cos(t)}\)
  • tiene dominio\(\left\{t: t \neq \frac{\pi}{2}+\pi k, \text { for integers } k\right\}=\bigcup_{k=-\infty}^{\infty}\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\)
  • tiene rango\(\{ u : |u| \geq 1 \} = (-\infty, -1] \cup [1, \infty)\)
• La función\(G(t) = \csc(t) = \dfrac{1}{\sin(t)}\)
  • tiene dominio\(\{t: t \neq \pi k, \text { for integers } k\}=\bigcup_{k=-\infty}^{\infty}(k \pi,(k+1) \pi)\)
  • tiene rango\(\{ u : |u| \geq 1 \} = (-\infty, -1] \cup [1, \infty)\)
• La función\(J(t) = \tan(t) = \dfrac{\sin(t)}{\cos(t)}\)
  • tiene dominio\(\left\{t: t \neq \frac{\pi}{2}+\pi k, \text { for integers } k\right\}=\bigcup_{k=-\infty}^{\infty}\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\)
  • tiene rango\((-\infty, \infty)\)
• La función\(K(t) = \cot(t) = \dfrac{\cos(t)}{\sin(t)}\)
  • tiene dominio\(\{t: t \neq \pi k, \text { for integers } k\}=\bigcup_{k=-\infty}^{\infty}(k \pi,(k+1) \pi)\)
  • tiene rango\((-\infty, \infty)\)

Cerramos esta sección con algunas notas sobre la resolución de ecuaciones que involucran las funciones circulares. En primer lugar, la discusión en la página 735 en la Sección 10.2.1 relativa a la resolución de ecuaciones se aplica a las seis funciones circulares, no solo\(f(t) = \cos(t)\) y\(g(t) = \sin(t)\). En particular, para resolver la ecuación\(\cot(t) = -1\) para números reales\(t\), podemos usar el mismo proceso de pensamiento que usamos en el Ejemplo 10.3.2, número 3\(\cot(\theta) = -1\) para resolver ángulos\(\theta\) en medida de radianes, solo necesitamos recordar escribir nuestras respuestas usando la variable\(t\) como opuesto a\(\theta\). A continuación, es fundamental que conozcas los dominios y rangos de las seis funciones circulares para que sepas qué ecuaciones no tienen soluciones. Por ejemplo, no\(\sec(t) = \frac{1}{2}\) tiene solución porque no\(\frac{1}{2}\) está en el rango de secante. Por último, deberá revisar las nociones de ángulos de referencia y ángulos coterminales para que pueda ver por qué\(\csc(t) = -42\) tiene un conjunto infinito de soluciones en el Cuadrante III y otro conjunto infinito de soluciones en el Cuadrante IV.

10.3.2 Ejercicios

En Ejercicios 1 - 20, encuentra el valor exacto o indica que está indefinido.

1. \(\tan \left( \dfrac{\pi}{4} \right)\)
2. \(\sec \left( \dfrac{\pi}{6} \right)\)
3. \(\csc \left( \dfrac{5\pi}{6} \right)\)
4. \(\cot \left( \dfrac{4\pi}{3} \right)\)
5. \(\tan \left( -\dfrac{11\pi}{6} \right)\)
6. \(\sec \left( -\dfrac{3\pi}{2} \right)\)
7. \(\csc \left( -\dfrac{\pi}{3} \right)\)
8. \(\cot \left( \dfrac{13\pi}{2} \right)\)
9. \(\tan \left( 117\pi \right)\)
10. \(\sec \left( -\dfrac{5\pi}{3} \right)\)
11. \(\csc \left( 3\pi \right)\)
12. \(\cot \left( -5\pi \right)\)
13. \(\tan \left( \dfrac{31\pi}{2} \right)\)
14. \(\sec \left( \dfrac{\pi}{4} \right)\)
15. \(\csc \left( -\dfrac{7\pi}{4} \right)\)
16. \(\cot \left( \dfrac{7\pi}{6} \right)\)
17. \(\tan \left( \dfrac{2\pi}{3} \right)\)
18. \(\sec \left( -7\pi \right)\)
19. \(\csc \left( \dfrac{\pi}{2} \right)\)
20. \(\cot \left( \dfrac{3\pi}{4} \right)\)

En Ejercicios 21 - 34, utilice la información dada para encontrar los valores exactos de las funciones circulares restantes de\(\theta\).

21. \(\sin(\theta) = \dfrac{3}{5}\)con\(\theta\) en Cuadrante II
22. \(\tan(\theta) = \dfrac{12}{5}\)con\(\theta\) en Cuadrante III
23. \(\csc(\theta) = \dfrac{25}{24}\)con\(\theta\) en Cuadrante I
24. \(\sec(\theta) = 7\)con\(\theta\) en el Cuadrante IV
25. \(\csc(\theta) = -\dfrac{10\sqrt{91}}{91}\)con\(\theta\) en Cuadrante III
26. \(\cot(\theta) = -23\)con\(\theta\) en Cuadrante II
27. \(\tan(\theta) = -2\)con\(\theta\) en el Cuadrante IV.
28. \(\sec(\theta) = -4\)con\(\theta\) en el Cuadrante II.
29. \(\cot(\theta) = \sqrt{5}\)con\(\theta\) en el Cuadrante III.
30. \(\cos(\theta) = \dfrac{1}{3}\)con\(\theta\) en el Cuadrante I.
31. \(\cot(\theta) = 2\)con\(0 < \theta < \dfrac{\pi}{2}\).
32. \(\csc(\theta) = 5\)con\(\dfrac{\pi}{2} < \theta < \pi\).
33. \(\tan(\theta) = \sqrt{10}\)con\(\pi < \theta < \dfrac{3\pi}{2}\).
34. \(\sec(\theta) = 2\sqrt{5}\)con\(\dfrac{3\pi}{2} < \theta < 2\pi\).

En los Ejercicios 35 - 42, usa tu calculadora para aproximar el valor dado a tres decimales. ¡Asegúrate de que tu calculadora esté en el modo de medición de ángulo adecuado!

35. \(\csc(78.95^{\circ})\)
36. \(\tan(-2.01)\)
37. \(\cot(392.994)\)
38. \(\sec(207^{\circ})\)
39. \(\csc(5.902)\)
40. \(\tan(39.672^{\circ})\)
41. \(\cot(3^{\circ})\)
42. \(\sec(0.45)\)

En los Ejercicios 43 - 57, encuentra todos los ángulos que satisfacen la ecuación.

43. \(\tan(\theta) = \sqrt{3}\)
44. \(\sec(\theta) = 2\)
45. \(\csc(\theta) = -1\)
46. \(\cot(\theta) = \dfrac{\sqrt{3}}{3}\)
47. \(\tan(\theta) = 0\)
48. \(\sec(\theta) = 1\)
49. \(\csc(\theta) = 2\)
50. \(\cot(\theta) = 0\)
51. \(\tan(\theta) = -1\)
52. \(\sec(\theta) = 0\)
53. \(\csc(\theta) = -\dfrac{1}{2}\)
54. \(\sec(\theta) = -1\)
55. \(\tan(\theta) = -\sqrt{3}\)
56. \(\csc(\theta) = -2\)
57. \(\cot(\theta) = -1\)

En Ejercicios 58 - 65, resuelve la ecuación para\(t\). Dar valores exactos.

58. \(\cot(t) = 1\)
59. \(\tan(t) = \dfrac{\sqrt{3}}{3}\)
60. \(\sec(t) = -\dfrac{2\sqrt{3}}{3}\)
61. \(\csc(t) = 0\)
62. \(\cot(t) = -\sqrt{3}\)
63. \(\tan(t) = -\dfrac{\sqrt{3}}{3}\)
64. \(\sec(t) = \dfrac{2\sqrt{3}}{3}\)
65. \(\csc(t) = \dfrac{2\sqrt{3}}{3}\)

En Ejercicios 66 - 69, utilice Teorema 10.10 para encontrar las cantidades solicitadas.

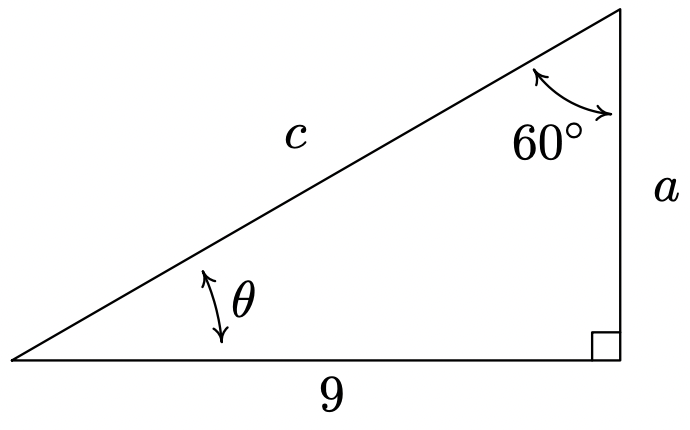
66. Encontrar\(\theta\),\(a\), y\(c\).

    

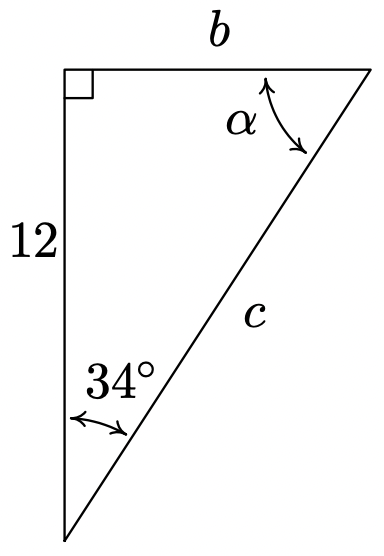
67. Encontrar\(\alpha\),\(b\), y\(c\).

    

68. Encontrar\(\theta\),\(a\), y\(c\).

    

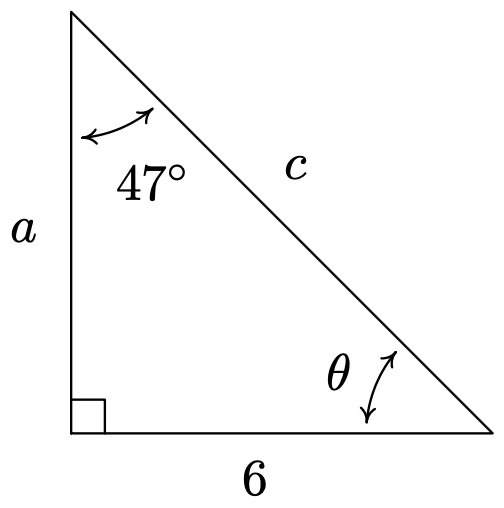
69. Encontrar\(\beta\),\(b\), y\(c\).

    

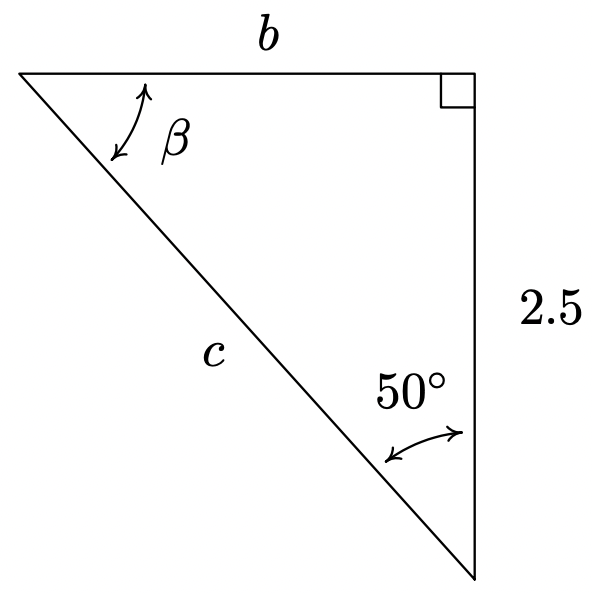
En los Ejercicios 70 - 75, utilice el Teorema 10.10 para responder a la pregunta. Supongamos que\(\theta\) es un ángulo en un triángulo rectángulo.

70. Si\(\theta = 30^{\circ}\) y el lado opuesto\(\theta\) tiene longitud\(4\), ¿cuánto tiempo es adyacente el lado\(\theta\)?
71. Si\(\theta = 15^{\circ}\) y la hipotenusa tiene longitud\(10\), ¿cuánto tiempo es el lado opuesto\(\theta\)?
72. Si\(\theta = 87^{\circ}\) y el lado adyacente a\(\theta\) tiene longitud\(2\), ¿cuánto tiempo es el lado opuesto\(\theta\)?
73. Si\(\theta = 38.2^{\circ}\) y el lado opuesto\(\theta\) tiene longitud\(14\), ¿cuánto dura la hipotenusa?
74. Si\(\theta = 2.05^{\circ}\) y la hipotenusa tiene longitud\(3.98\), ¿cuánto tiempo está adyacente el lado\(\theta\)?
75. Si\(\theta = 42^{\circ}\) y el lado adyacente a\(\theta\) tiene longitud\(31\), ¿cuánto tiempo es el lado opuesto\(\theta\)?
76. Un árbol de pie verticalmente sobre un terreno llano proyecta una sombra de 120 pies de largo. El ángulo de elevación desde el final de la sombra hasta la parte superior del árbol es\(21.4^{\circ}\). Encuentra la altura del árbol al pie más cercano. Con la ayuda de tus compañeros, investiga el término umbra versa y ve qué tiene que ver con la sombra en este problema.
77. La torre de transmisión para la estación de radio WSAZ (Hogar de “Álgebra en la Mañana con Carl y Jeff”) tiene dos enormes luces rojas intermitentes: una en la parte superior y otra a unos pies por debajo de la parte superior. Desde un punto a 5000 pies de distancia de la base de la torre en terreno llano el ángulo de elevación a la luz superior es\(7.970^{\circ}\) y a la segunda luz es\(7.125^{\circ}\). Encuentra la distancia entre las luces al pie más cercano.
78. En la página 753 definimos el ángulo de inclinación (también conocido como ángulo de elevación) y en este ejercicio introducimos un ángulo relacionado, el ángulo de depresión (también conocido como ángulo de declinación). El ángulo de depresión de un objeto se refiere al ángulo cuyo lado inicial es una línea horizontal por encima del objeto y cuyo lado terminal es la línea de visión al objeto por debajo de la horizontal. Esto se representa esquemáticamente a continuación.

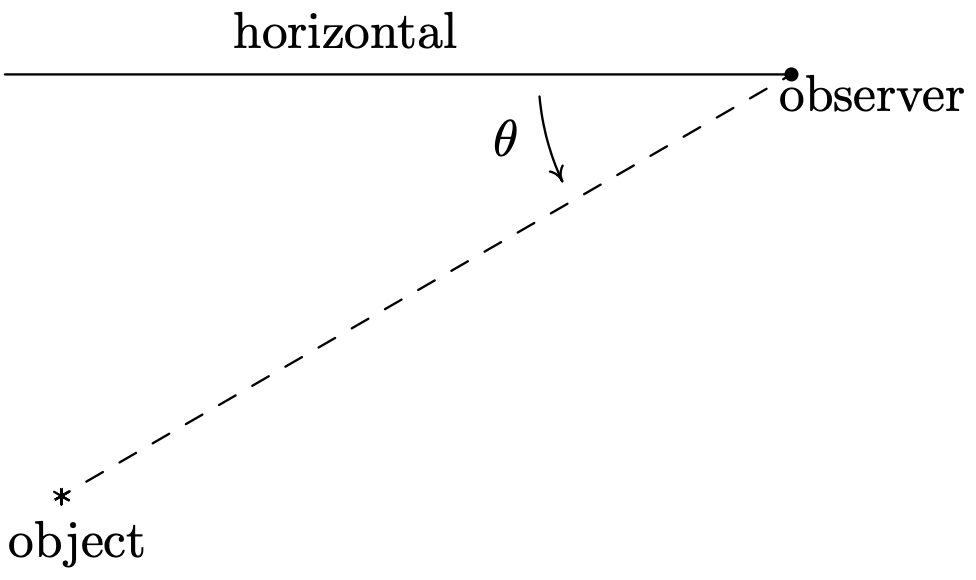    El ángulo de depresión desde la horizontal hasta el objeto es θ

    1. Mostrar que si la horizontal está por encima y es paralela al suelo nivelado entonces el ángulo de depresión (de observador a objeto) y el ángulo de inclinación (de objeto a observador) serán congruentes porque son ángulos interiores alternos.
    2. Desde una torre de bomberos a 200 pies sobre el nivel del suelo en el Bosque Nacional Sasquatch, un guardabosques ve un incendio en la distancia. El ángulo de depresión al fuego es de 2.5 ^o. ¿A qué distancia de la base de la torre está el fuego?
    3. El guardabosques en la parte 78b ve a un Sasquatch corriendo directamente del fuego hacia la torre de bomberos. El guardabosques se lleva dos avistamientos. En el primer avistamiento, el ángulo de depresión desde la torre hasta el Sasquatch es de 6 ^o. El segundo avistamiento, tomado apenas 10 segundos después, le da al ángulo de depresión como 6.5 ^o. ¿Hasta dónde viajó el Saquatch en esos 10 segundos? Redondea tu respuesta al pie más cercano. ¿Qué tan rápido corre en millas por hora? Redondee su respuesta a la milla por hora más cercana. Si el Sasquatch mantiene este ritmo, ¿cuánto tiempo tardará el Sasquatch en llegar a la torre de bomberos desde su ubicación en el segundo avistamiento? Redondee su respuesta al minuto más cercano.
79. Cuando estoy a 30 pies de distancia de un árbol en casa, el ángulo de elevación a la parte superior del árbol es\(50^{\circ}\) y el ángulo de depresión a la base del árbol lo es\(10^{\circ}\). ¿Cuál es la altura del árbol? Redondea tu respuesta al pie más cercano.
80. Desde la plataforma de observación del faro en Sasquatch Point a 50 pies sobre la superficie del lago Ippizuti, un socorrista ve un bote en el lago navegando directamente hacia el faro. El primer avistamiento tuvo un ángulo de depresión de\(8.2^{\circ}\) y el segundo avistamiento tuvo un ángulo de depresión de\(25.9^{\circ}\). ¿Hasta dónde había viajado el bote entre los avistamientos?
81. Un cable de sujeción de 1000 pies de largo está unido a la parte superior de una torre. Cuando se tira tensa hace un\(43^{\circ}\) ángulo con el suelo. ¿Qué tan alta es la torre? ¿A qué distancia de la base de la torre choca el cable contra el suelo?

En los Ejercicios 82 - 128, verificar la identidad. Supongamos que todas las cantidades están definidas.

82. \(\cos(\theta) \sec(\theta) = 1\)
83. \(\tan(\theta)\cos(\theta) = \sin(\theta)\)
84. \(\sin(\theta) \csc(\theta) = 1\)
85. \(\tan(\theta) \cot(\theta) = 1\)
86. \(\csc(\theta) \cos(\theta) = \cot(\theta)\)
87. \(\dfrac{\sin(\theta)}{\cos^{2}(\theta)} = \sec(\theta) \tan(\theta)\)
88. \(\dfrac{\cos(\theta)}{\sin^{2}(\theta)} = \csc(\theta) \cot(\theta)\)
89. \(\dfrac{1+ \sin(\theta)}{\cos(\theta)} = \sec(\theta) + \tan(\theta)\)
90. \(\dfrac{1 - \cos(\theta)}{\sin(\theta)} = \csc(\theta) - \cot(\theta)\)
91. \(\dfrac{\cos(\theta)}{1 - \sin^{2}(\theta)} = \sec(\theta)\)
92. \(\dfrac{\sin(\theta)}{1 - \cos^{2}(\theta)} = \csc(\theta)\)
93. \(\dfrac{\sec(\theta)}{1 + \tan^{2}(\theta)} = \cos(\theta)\)
94. \(\dfrac{\csc(\theta)}{1 + \cot^{2}(\theta)} = \sin(\theta)\)
95. \(\dfrac{\tan(\theta)}{\sec^{2}(\theta) - 1} = \cot(\theta)\)
96. \(\dfrac{\cot(\theta)}{\csc^{2}(\theta) - 1} = \tan(\theta)\)
97. \(4 \cos^{2}(\theta) + 4 \sin^{2}(\theta) = 4\)
98. \(9 - \cos^{2}(\theta) - \sin^{2}(\theta) = 8\)
99. \(\tan^{3}(\theta) = \tan(\theta)\sec^{2}(\theta) - \tan(\theta)\)
100. \(\sin^{5}(\theta) = \left(1-\cos^{2}(\theta)\right)^{2} \sin(\theta)\)
101. \(\sec^{10}(\theta) = \left(1 + \tan^{2}(\theta)\right)^4 \sec^{2}(\theta)\)
102. \(\cos^{2}(\theta)\tan^{3}(\theta) = \tan(\theta) - \sin(\theta)\cos(\theta)\)
103. \(\sec^{4}(\theta) - \sec^{2}(\theta) = \tan^{2}(\theta) + \tan^{4}(\theta)\)
104. \(\dfrac{\cos(\theta) + 1}{\cos(\theta) - 1} = \dfrac{1 + \sec(\theta)}{1 - \sec(\theta)}\)
105. \(\dfrac{\sin(\theta) + 1}{\sin(\theta) - 1} = \dfrac{1 + \csc(\theta)}{1 - \csc(\theta)}\)
106. \(\dfrac{1 - \cot(\theta)}{1+ \cot(\theta)} = \dfrac{\tan(\theta) - 1}{\tan(\theta) + 1}\)
107. \(\dfrac{1 - \tan(\theta)}{1+ \tan(\theta)} = \dfrac{\cos(\theta) - \sin(\theta)}{\cos(\theta) + \sin(\theta)}\)
108. \(\tan(\theta) + \cot(\theta) = \sec(\theta)\csc(\theta)\)
109. \(\csc(\theta) - \sin(\theta) = \cot(\theta)\cos(\theta)\)
110. \(\cos(\theta) - \sec(\theta) = -\tan(\theta)\sin(\theta)\)
111. \(\cos(\theta)(\tan(\theta) + \cot(\theta)) = \csc(\theta)\)
112. \(\sin(\theta)(\tan(\theta) + \cot(\theta)) = \sec(\theta)\)
113. \(\dfrac{1}{1-\cos(\theta)} + \dfrac{1}{1+\cos(\theta)} = 2\csc^{2}(\theta)\)
114. \(\dfrac{1}{\sec(\theta) + 1} + \dfrac{1}{\sec(\theta)-1} = 2 \csc(\theta) \cot(\theta)\)
115. \(\dfrac{1}{\csc(\theta) + 1} + \dfrac{1}{\csc(\theta)-1} = 2 \sec(\theta) \tan(\theta)\)
116. \(\dfrac{1}{\csc(\theta)-\cot(\theta)} - \dfrac{1}{\csc(\theta) + \cot(\theta)} = 2 \cot(\theta)\)
117. \(\dfrac{\cos(\theta)}{1 - \tan(\theta)} + \dfrac{\sin(\theta)}{1 - \cot(\theta)} = \sin(\theta) + \cos(\theta)\)
118. \(\dfrac{1}{\sec(\theta) + \tan(\theta)} = \sec(\theta) - \tan(\theta)\)
119. \(\dfrac{1}{\sec(\theta) - \tan(\theta)} = \sec(\theta) + \tan(\theta)\)
120. \(\dfrac{1}{\csc(\theta) - \cot(\theta)} = \csc(\theta) + \cot(\theta)\)
121. \(\dfrac{1}{\csc(\theta) + \cot(\theta)} = \csc(\theta) - \cot(\theta)\)
122. \(\dfrac{1}{1-\sin(\theta)} = \sec^{2}(\theta) + \sec(\theta) \tan(\theta)\)
123. \(\dfrac{1}{1+\sin(\theta)} = \sec^{2}(\theta) - \sec(\theta) \tan(\theta)\)
124. \(\dfrac{1}{1-\cos(\theta)} = \csc^{2}(\theta) + \csc(\theta) \cot(\theta)\)
125. \(\dfrac{1}{1+\cos(\theta)} = \csc^{2}(\theta) - \csc(\theta) \cot(\theta)\)
126. \(\dfrac{\cos(\theta)}{1 + \sin(\theta)} = \dfrac{1-\sin(\theta)}{\cos(\theta)}\)
127. \(\csc(\theta) - \cot(\theta) = \dfrac{\sin(\theta)}{1 + \cos(\theta)}\)
128. \(\dfrac{1 - \sin(\theta)}{1 + \sin(\theta)} = (\sec(\theta) - \tan(\theta))^{2}\)

En los Ejercicios 129 - 132, verificar la identidad. Es posible que deba consultar las Secciones 2.2 y 6.2 para una revisión de las propiedades de valor absoluto y logaritmos antes de continuar.

129. \(\quad \ln|\sec(\theta)| = -\ln|\cos(\theta)|\)
130. \(-\ln|\csc(\theta)| = \ln|\sin(\theta)|\)
131. \(-\ln|\sec(\theta) - \tan(\theta)| = \ln|\sec(\theta)+\tan(\theta)|\)
132. \(-\ln|\csc(\theta) + \cot(\theta)|= \ln|\csc(\theta) - \cot(\theta)|\)
133. Verificar los dominios y rangos de las funciones tangente, cosecante y cotangente tal como se presenta en el Teorema 10.11.
134. Como hicimos en el Ejercicio 74 de la Sección 10.2, dejemos\(\alpha\) y\(\beta\) sean los dos ángulos agudos de un triángulo rectángulo. (Así\(\alpha\) y\(\beta\) son ángulos complementarios.) Demuestre eso\(\sec(\alpha) = \csc(\beta)\) y\(\tan(\alpha) = \cot(\beta)\). El hecho de que las cofunciones de los ángulos complementarios sean iguales en este caso no es un accidente y se dará un resultado más general en la Sección 10.4.
135. Deseamos establecer la desigualdad\(\cos(\theta) < \dfrac{\sin(\theta)}{\theta} < 1\) para\(0 < \theta < \dfrac{\pi}{2}.\) Usar el diagrama desde el inicio de la sección, parcialmente reproducido a continuación, para responder a lo siguiente.

     

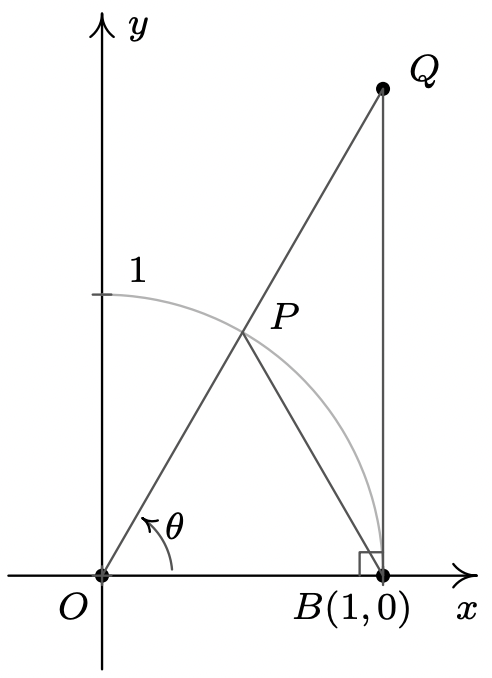
     1. Demuestre que el triángulo\(OPB\) tiene área\(\dfrac{1}{2} \sin(\theta)\).
     2. Demostrar que el sector circular\(OPB\) con ángulo central\(\theta\) tiene área\(\dfrac{1}{2} \theta\).
     3. Demuestre que el triángulo\(OQB\) tiene área\(\dfrac{1}{2} \tan(\theta)\).
     4. Comparando áreas, demuéstralo\(\sin(\theta) < \theta < \tan(\theta)\) para\(0 < \theta < \dfrac{\pi}{2}.\)
     5. Usa la desigualdad\(\sin(\theta) < \theta\) para demostrarlo\(\dfrac{\sin(\theta)}{\theta} < 1\) por\(0 < \theta < \dfrac{\pi}{2}.\)
     6. Usa la desigualdad\(\theta < \tan(\theta)\) para demostrar que\(\cos(\theta) < \dfrac{\sin(\theta)}{\theta}\) para\(0 < \theta < \dfrac{\pi}{2}.\) Combine esto con la parte anterior para completar la prueba.
136. Demostrar que\(\cos(\theta) < \dfrac{\sin(\theta)}{\theta} < 1\) también se sostiene para\(-\dfrac{\pi}{2}< \theta < 0\).
137. Explicar por qué el hecho de que eso\(\tan(\theta) = 3 = \frac{3}{1}\) no significa\(\sin(\theta) = 3\) y\(\cos(\theta) = 1\)? (Ver la solución al número 6 en el Ejemplo 10.3.1.)

10.3.3 Respuestas

1. \(\tan \left( \dfrac{\pi}{4} \right) = 1\)
2. \(\sec \left( \dfrac{\pi}{6} \right) = \dfrac{2\sqrt{3}}{3}\)
3. \(\csc \left( \dfrac{5\pi}{6} \right) = 2\)
4. \(\cot \left( \dfrac{4\pi}{3} \right) = \dfrac{\sqrt{3}}{3}\)
5. \(\tan \left( -\dfrac{11\pi}{6} \right) = \dfrac{\sqrt{3}}{3}\)
6. \(\sec \left( -\dfrac{3\pi}{2} \right)\)está indefinido
7. \(\csc \left( -\dfrac{\pi}{3} \right) = -\dfrac{2\sqrt{3}}{3}\)
8. \(\cot \left( \dfrac{13\pi}{2} \right) = 0\)
9. \(\tan \left( 117\pi \right) = 0\)
10. \(\sec \left( -\dfrac{5\pi}{3} \right) = 2\)
11. \(\csc \left( 3\pi \right)\)está indefinido
12. \(\cot \left( -5\pi \right)\)está indefinido
13. \(\tan \left( \dfrac{31\pi}{2} \right)\)está indefinido
14. \(\sec \left( \dfrac{\pi}{4} \right) = \sqrt{2}\)
15. \(\csc \left( -\dfrac{7\pi}{4} \right) = \sqrt{2}\)
16. \(\cot \left( \dfrac{7\pi}{6} \right) = \sqrt{3}\)
17. \(\tan \left( \dfrac{2\pi}{3} \right) = -\sqrt{3}\)
18. \(\sec \left( -7\pi \right) = -1\)
19. \(\csc \left( \dfrac{\pi}{2} \right) = 1\)
20. \(\cot \left( \dfrac{3\pi}{4} \right) = -1\)
21. \(\sin(\theta) = \frac{3}{5}, \cos(\theta) = -\frac{4}{5}, \tan(\theta) = -\frac{3}{4}, \csc(\theta) = \frac{5}{3}, \sec(\theta) = -\frac{5}{4}, \cot(\theta) = -\frac{4}{3}\)
22. \(\sin(\theta) = -\frac{12}{13}, \cos(\theta) = -\frac{5}{13}, \tan(\theta) = \frac{12}{5}, \csc(\theta) = -\frac{13}{12}, \sec(\theta) = -\frac{13}{5}, \cot(\theta) = \frac{5}{12}\)
23. \(\sin(\theta) = \frac{24}{25}, \cos(\theta) = \frac{7}{25}, \tan(\theta) = \frac{24}{7}, \csc(\theta) = \frac{25}{24}, \sec(\theta) = \frac{25}{7}, \cot(\theta) = \frac{7}{24}\)
24. \(\sin(\theta) = \frac{-4\sqrt{3}}{7}, \cos(\theta) = \frac{1}{7}, \tan(\theta) = -4\sqrt{3}, \csc(\theta) = -\frac{7\sqrt{3}}{12}, \sec(\theta) = 7, \cot(\theta) = -\frac{\sqrt{3}}{12}\)
25. \(\sin(\theta) = -\frac{\sqrt{91}}{10}, \cos(\theta) = -\frac{3}{10}, \tan(\theta) = \frac{\sqrt{91}}{3}, \csc(\theta) = -\frac{10\sqrt{91}}{91}, \sec(\theta) = -\frac{10}{3}, \cot(\theta) = \frac{3\sqrt{91}}{91}\)
26. \(\sin(\theta) = \frac{\sqrt{530}}{530}, \cos(\theta) = -\frac{23\sqrt{530}}{530}, \tan(\theta) = -\frac{1}{23}, \csc(\theta) = \sqrt{530}, \sec(\theta) = -\frac{\sqrt{530}}{23}, \cot(\theta) = -23\)
27. \(\sin(\theta) = -\frac{2\sqrt{5}}{5}, \cos(\theta) = \frac{\sqrt{5}}{5}, \tan(\theta) = -2, \csc(\theta) = -\frac{\sqrt{5}}{2}, \sec(\theta) = \sqrt{5}, \cot(\theta) = -\frac{1}{2}\)
28. \(\sin(\theta) = \frac{\sqrt{15}}{4}, \cos(\theta) = -\frac{1}{4}, \tan(\theta) = -\sqrt{15}, \csc(\theta) = \frac{4\sqrt{15}}{15}, \sec(\theta) = -4, \cot(\theta) = -\frac{\sqrt{15}}{15}\)
29. \(\sin(\theta) = -\frac{\sqrt{6}}{6}, \cos(\theta) = -\frac{\sqrt{30}}{6}, \tan(\theta) = \frac{\sqrt{5}}{5}, \csc(\theta) = -\sqrt{6}, \sec(\theta) = -\frac{\sqrt{30}}{5}, \cot(\theta) = \sqrt{5}\)
30. \(\sin(\theta) = \frac{2\sqrt{2}}{3}, \cos(\theta) = \frac{1}{3}, \tan(\theta) = 2\sqrt{2}, \csc(\theta) = \frac{3\sqrt{2}}{4}, \sec(\theta) = 3, \cot(\theta) = \frac{\sqrt{2}}{4}\)
31. \(\sin(\theta) = \frac{\sqrt{5}}{5}, \cos(\theta) = \frac{2\sqrt{5}}{5}, \tan(\theta) = \frac{1}{2}, \csc(\theta) = \sqrt{5}, \sec(\theta) = \frac{\sqrt{5}}{2}, \cot(\theta) = 2\)
32. \(\sin(\theta) = \frac{1}{5}, \cos(\theta) = -\frac{2\sqrt{6}}{5}, \tan(\theta) = -\frac{\sqrt{6}}{12}, \csc(\theta) = 5, \sec(\theta) = -\frac{5\sqrt{6}}{12}, \cot(\theta) = -2\sqrt{6}\)
33. \(\sin(\theta) = -\frac{\sqrt{110}}{11}, \cos(\theta) = -\frac{\sqrt{11}}{11}, \tan(\theta) = \sqrt{10}, \csc(\theta) = -\frac{\sqrt{110}}{10}, \sec(\theta) = -\sqrt{11}, \cot(\theta) = \frac{\sqrt{10}}{10}\)
34. \(\sin(\theta) = -\frac{\sqrt{95}}{10}, \cos(\theta) = \frac{\sqrt{5}}{10}, \tan(\theta) = -\sqrt{19}, \csc(\theta) = -\frac{2\sqrt{95}}{19}, \sec(\theta) = 2\sqrt{5}, \cot(\theta) = -\frac{\sqrt{19}}{19}\)
35. \(\csc(78.95^{\circ}) \approx 1.019\)
36. \(\tan(-2.01) \approx 2.129\)
37. \(\cot(392.994) \approx 3.292\)
38. \(\sec(207^{\circ}) \approx -1.122\)
39. \(\csc(5.902) \approx -2.688\)
40. \(\tan(39.672^{\circ}) \approx 0.829\)
41. \(\cot(3^{\circ}) \approx 19.081\)
42. \(\sec(0.45) \approx 1.111\)
43. \(\tan(\theta) = \sqrt{3}\)cuando\(\theta = \dfrac{\pi}{3} + \pi k\) para cualquier entero\(k\)
44. \(\sec(\theta) = 2\)cuando\(\theta = \dfrac{\pi}{3} + 2\pi k\) o\(\theta = \dfrac{5\pi}{3} + 2\pi k\) para cualquier entero\(k\)
45. \(\csc(\theta) = -1\)cuando\(\theta = \dfrac{3\pi}{2} + 2\pi k\) para cualquier entero\(k\).
46. \(\cot(\theta) = \dfrac{\sqrt{3}}{3}\)cuando\(\theta = \dfrac{\pi}{3} + \pi k\) para cualquier entero\(k\)
47. \(\tan(\theta) = 0\)cuando\(\theta = \pi k\) para cualquier entero\(k\)
48. \(\sec(\theta) = 1\)cuando\(\theta = 2\pi k\) para cualquier entero\(k\)
49. \(\csc(\theta) = 2\)cuando\(\theta = \dfrac{\pi}{6} + 2\pi k\) o\(\theta = \dfrac{5\pi}{6} + 2\pi k\) para cualquier entero\(k\).
50. \(\cot(\theta) = 0\)cuando\(\theta = \dfrac{\pi}{2} + \pi k\) para cualquier entero\(k\)
51. \(\tan(\theta) = -1\)cuando\(\theta = \dfrac{3\pi}{4} + \pi k\) para cualquier entero\(k\)
52. \(\sec(\theta) = 0\)nunca pasa
53. \(\csc(\theta) = -\dfrac{1}{2}\)nunca pasa
54. \(\sec(\theta) = -1\)cuando\(\theta = \pi + 2\pi k = (2k+1)\pi\) para cualquier entero\(k\)
55. \(\tan(\theta) = -\sqrt{3}\)cuando\(\theta = \dfrac{2\pi}{3} + \pi k\) para cualquier entero\(k\)
56. \(\csc(\theta) = -2\)cuando\(\theta = \dfrac{7\pi}{6} + 2\pi k\) o\(\theta = \dfrac{11\pi}{6} + 2\pi k\) para cualquier entero\(k\)
57. \(\cot(\theta) = -1\)cuando\(\theta = \dfrac{3\pi}{4} + \pi k\) para cualquier entero\(k\)
58. \(\cot(t) = 1\)cuando\(t = \dfrac{\pi}{4} + \pi k\) para cualquier entero\(k\)
59. \(\tan(t) = \dfrac{\sqrt{3}}{3}\)cuando\(t = \dfrac{\pi}{6} + \pi k\) para cualquier entero\(k\)
60. \(\sec(t) = -\dfrac{2\sqrt{3}}{3}\)cuando\(t = \dfrac{5\pi}{6} + 2\pi k\) o\(t = \dfrac{7\pi}{6} + 2\pi k\) para cualquier entero\(k\)
61. \(\csc(t) = 0\)nunca pasa
62. \(\cot(t) = -\sqrt{3}\)cuando\(t = \dfrac{5\pi}{6} + \pi k\) para cualquier entero\(k\)
63. \(\tan(t) = -\dfrac{\sqrt{3}}{3}\)cuando\(t = \dfrac{5\pi}{6} + \pi k\) para cualquier entero\(k\)
64. \(\sec(t) = \dfrac{2\sqrt{3}}{3}\)cuando\(t = \dfrac{\pi}{6} + 2\pi k\) o\(t = \dfrac{11\pi}{6} + 2\pi k\) para cualquier entero\(k\)
65. \(\csc(t) = \dfrac{2\sqrt{3}}{3}\)cuando\(t = \dfrac{\pi}{3} + 2\pi k\) o\(t = \dfrac{2\pi}{3} + 2\pi k\) para cualquier entero\(k\)
66. \(\theta = 30^{\circ}\),\(a = 3\sqrt{3}\),\(c = \sqrt{108} = 6\sqrt{3}\)
67. \(\alpha = 56^{\circ}\),\(b = 12 \tan(34^{\circ}) = 8.094\),\(c = 12\sec(34^{\circ}) = \dfrac{12}{\cos(34^{\circ})} \approx 14.475\)
68. \(\theta = 43^{\circ}\),\(a = 6\cot(47^{\circ}) = \dfrac{6}{\tan(47^{\circ})} \approx 5.595\),\(c = 6\csc(47^{\circ}) = \dfrac{6}{\sin(47^{\circ})} \approx 8.204\)
69. \(\beta = 40^{\circ}\),\(b = 2.5 \tan(50^{\circ}) \approx 2.979\),\(c = 2.5\sec(50^{\circ}) = \dfrac{2.5}{\cos(50^{\circ})} \approx 3.889\)
70. El lado adyacente a\(\theta\) tiene longitud\(4\sqrt{3} \approx 6.928\)
71. El lado opuesto\(\theta\) tiene longitud\(10 \sin(15^{\circ}) \approx 2.588\)
72. El lado opuesto\(\theta\) es\(2\tan(87^{\circ}) \approx 38.162\)
73. La hipotenusa tiene longitud\(14 \csc(38.2^{\circ}) = \dfrac{14}{\sin(38.2^{\circ})} \approx 22.639\)
74. El lado adyacente a\(\theta\) tiene longitud\(3.98 \cos(2.05^{\circ}) \approx 3.977\)
75. El lado opuesto\(\theta\) tiene longitud\(31\tan(42^{\circ}) \approx 27.912\)
76. El árbol mide aproximadamente 47 pies de altura.
77. Las luces están a unos 75 pies de distancia.
78. 1. El fuego está a unos 4581 pies de la base de la torre.
    2. El Sasquatch corrió\(200\cot(6^{\circ}) - 200\cot(6.5^{\circ}) \approx 147\) pies en esos 10 segundos. Esto se traduce en\(\approx 10\) millas por hora. En el lugar del segundo avistamiento, el Sasquatch estaba a\(\approx 1755\) pies de la torre, lo que significa que, si mantiene este ritmo, llegará a la torre en unos\(2\) minutos.
79. El árbol mide aproximadamente 41 pies de altura.
80. El barco ha recorrido unos 244 pies.
81. La torre mide aproximadamente 682 pies de altura. El cable tipo choca contra el suelo a unos 731 pies de distancia de la base de la torre.

---

Referencia

¹ En el Teorema 10.4 también mostramos coseno y seno como funciones de un ángulo residiendo en un triángulo rectángulo por lo que podríamos llamarlos fácilmente funciones trigonométricas. En secciones posteriores, encontrará que efectivamente usamos la frase 'función trigonométrica' indistintamente con el término 'función circular'.

² Compárelo con la definición dada en la Sección 2.1.

³ Como veremos en breve, al resolver ecuaciones que involucran secante y cosecante, solemos convertir de nuevo a cosenos y senos. Sin embargo, a la hora de resolver por tangente o cotangente, generalmente nos apegamos a lo que nos tratan.

⁴ Véase el Ejemplo 10.2.5 número 3 en la Sección 10.2 para otro ejemplo de este tipo de simplificación de la solución.

⁵ O, para decirlo de otra manera, ¡gana más crédito parcial si esto fuera una pregunta de examen!

⁶ Podremos elegir cualquier valor\(x\) y\(y\) siempre y cuando\(x>0, y<0\) y\(\frac{x}{y}=-4\). Por ejemplo, podríamos elegir\(x = 8\) y\(y = −2\). El hecho de que todos estos puntos se encuentren en el lado terminal de\(\theta\) es consecuencia de que el lado terminal de\(\theta\) es la porción de la línea con pendiente\(-\frac{1}{4}\) que se extiende desde el origen hacia el cuadrante IV.

⁷ Nombrado en honor a Raymond Q. Armington, la Torre del Reloj de Lakeland forma parte del campus desde 1972.

⁸ Usando el Teorema 2.4 de la Sección 2.4.

⁹ Observe que hemos utilizado la variable\(u\) '' como la 'variable ficticia 'para describir los elementos de rango. Si bien no hay razón matemática para hacer esto (estamos describiendo un conjunto de números reales, y, como tal, podría usar de\(t\) nuevo) elegimos ayudar\(u\) a solidificar la idea de que estos números reales son las salidas de las entradas, a las que hemos venido llamando\(t\).