10.4: Identidades trigonométricas

En la Sección 10.3, vimos la utilidad de las Identidades Pitágoras en el Teorema 10.8 junto con el Cociente y las Identidades Recíprocas en el Teorema 10.6. Estas identidades no solo nos ayudaron a calcular los valores de las funciones circulares para ángulos, sino que también fueron útiles para simplificar expresiones que involucran las funciones circulares. En esta sección, presentamos varias colecciones de identidades que tienen usos en este curso y más allá. Nuestro primer conjunto de identidades son las identidades 'Pares/Impares'. ¹

Teorema 10.12. Identidades pares/impares

Para todos los ángulos aplicables\(\theta\),

• \(\cos(-\theta) = \cos(\theta)\)
• \(\sec(-\theta) = \sec(\theta)\)
• \(\sin(-\theta) = -\sin(\theta)\)
• \(\csc(-\theta) = -\csc(\theta)\)
• \(\tan(-\theta) = -\tan(\theta)\)
• \(\cot(-\theta) = -\cot(\theta)\)

A la luz del Cociente y las Identidades Recíprocas, Teorema 10.6, basta con mostrar\(\cos(-\theta) = \cos(\theta)\) y\(\sin(-\theta) = -\sin(\theta)\). Las cuatro funciones circulares restantes se pueden expresar en términos de\(\cos(\theta)\) y\(\sin(\theta)\) así las pruebas de sus Identidades Pares/Impares se dejan como ejercicios. Considera un ángulo\(\theta\) trazado en posición estándar. Dejar\(\theta_0\) ser el ángulo coterminal con\(\theta\) con\(0 \leq \theta_0 < 2\pi\). (Podemos construir el ángulo\(\theta_0\) girando en sentido antihorario desde el\(x\) eje positivo hasta el lado terminal\(\theta\) como se muestra a continuación). Desde\(\theta\) y\(\theta_0\) son coterminales,\(\cos(\theta) = \cos(\theta_0)\) y\(\sin(\theta) = \sin(\theta_0)\).

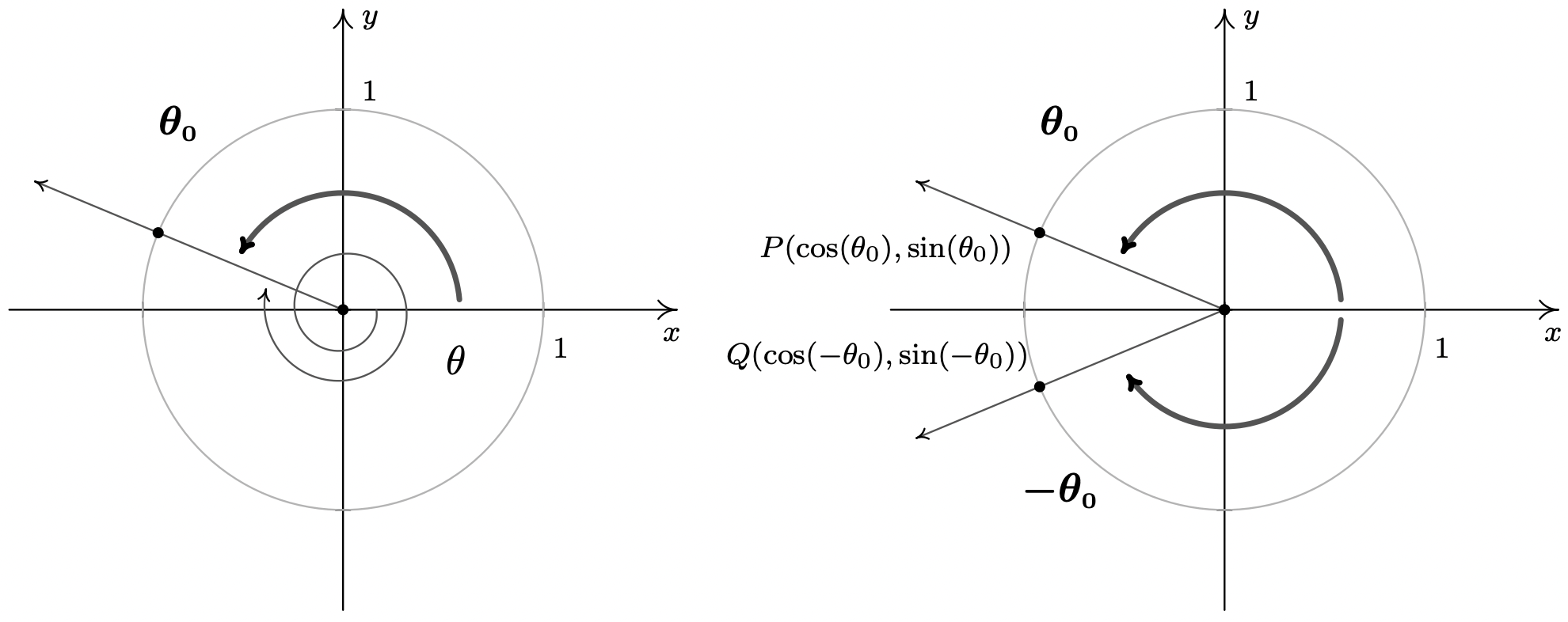
Consideramos ahora los ángulos\(-\theta\) y\(-\theta_0\). Ya que\(\theta\) es coterminal con\(\theta_0\), hay algún entero\(k\) así que eso\(\theta = \theta_0 + 2\pi \cdot k\). Por lo tanto,\(-\theta = -\theta_0 - 2\pi \cdot k = -\theta_0 + 2\pi \cdot(-k)\). Dado que\(k\) es un entero, así es\((-k)\), lo que significa que\(-\theta\) es coterminal con\(-\theta_0\). De ahí,\(\cos(-\theta) = \cos(-\theta_0)\) y\(\sin(-\theta) = \sin(-\theta_0)\). Dejar\(P\) y\(Q\) denotar los puntos en los lados terminales de\(\theta_0\) y\(-\theta_0\), respectivamente, que se encuentran en el Círculo de Unidad. Por definición, las coordenadas de\(P\) son\((\cos(\theta_0),\sin(\theta_0))\) y las coordenadas de\(Q\) son\((\cos(-\theta_0),\sin(-\theta_0))\). Dado que\(\theta_0\) y\(-\theta_0\) barrer sectores centrales congruentes del Círculo de Unidad, se deduce que los puntos\(P\) y\(Q\) son simétricos alrededor del\(x\) eje -eje. Así,\(\cos(-\theta_0) = \cos(\theta_0)\) y\(\sin(-\theta_0) = -\sin(\theta_0)\). Ya que los cosenos y senos de\(\theta_0\) y\(-\theta_0\) son los mismos que los para\(\theta\) y\(-\theta\), respectivamente, obtenemos\(\cos(-\theta) = \cos(\theta)\) y\(\sin(-\theta) = -\sin(\theta)\), según se requiera. Las Identidades Pares/Impares se demuestran fácilmente utilizando cualquiera de los 'ángulos comunes' señalados en la Sección 10.2. Su verdadera utilidad, sin embargo, no radica en el cálculo, sino en simplificar las expresiones que involucran las funciones circulares. De hecho, nuestro siguiente lote de identidades hace un uso intensivo de las identidades pares/impares.

Teorema 10.13. Identidades de suma y diferencia para coseno

Para todos los ángulos\(\alpha\) y\(\beta\),

• \(\cos(\alpha + \beta) = \cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)\)
• \(\cos(\alpha - \beta) = \cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta)\)

Primero probamos el resultado para las diferencias. Al igual que en la prueba de las Identidades Pares/Impares, podemos reducir la prueba para ángulos generales\(\alpha\) y\(\beta\) a ángulos\(\alpha_0\) y\(\beta_0\), coterminal con\(\alpha\) y\(\beta\), respectivamente, cada uno de los cuales mide entre\(0\) y\(2\pi\) radianes. Ya que\(\alpha\) y\(\alpha_0\) son coterminales, como son\(\beta\) y\(\beta_0\), se deduce que\(\alpha - \beta\) es coterminal con\(\alpha_0 - \beta_0\). Considera el caso a continuación donde\(\alpha_0 \geq \beta_0\).

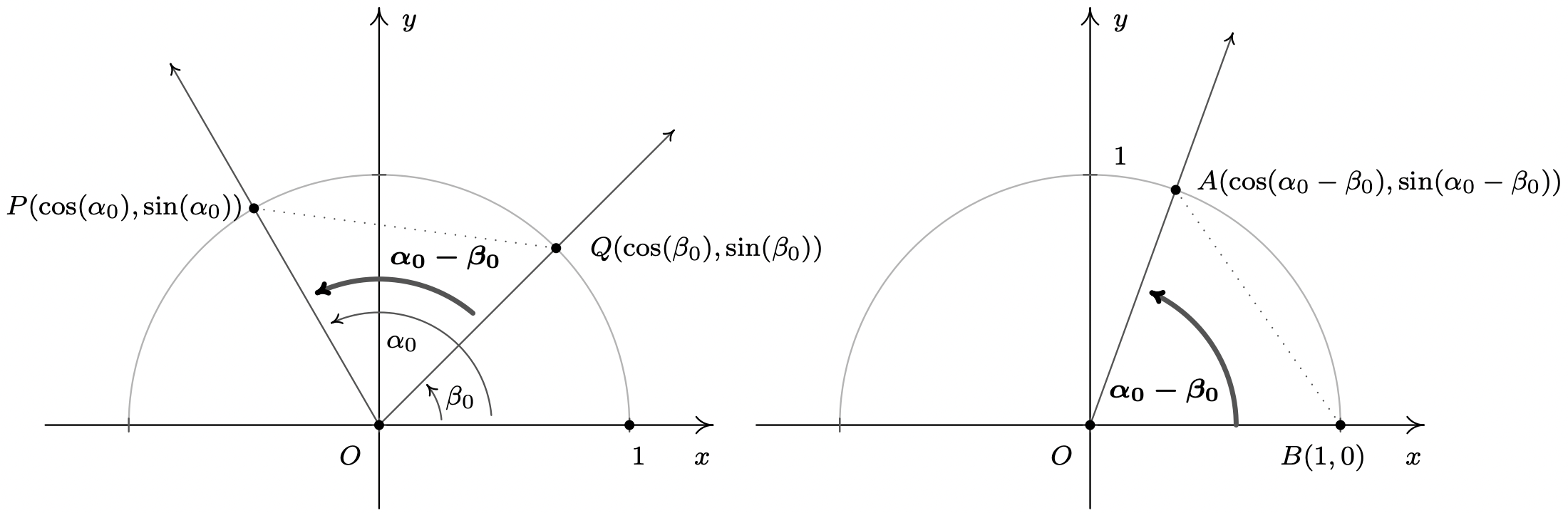
Dado que los ángulos\(POQ\) y\(AOB\) son congruentes, la distancia entre\(P\) y\(Q\) es igual a la distancia entre\(A\) y\(B\). ² La fórmula de distancia, Ecuación 1.1, rinde

\[\sqrt{\left(\cos \left(\alpha_{0}\right)-\cos \left(\beta_{0}\right)\right)^{2}+\left(\sin \left(\alpha_{0}\right)-\sin \left(\beta_{0}\right)\right)^{2}}=\sqrt{\left(\cos \left(\alpha_{0}-\beta_{0}\right)-1\right)^{2}+\left(\sin \left(\alpha_{0}-\beta_{0}\right)-0\right)^{2}}\nonumber\]

Al cuadrar ambos lados, expandimos el lado izquierdo de esta ecuación como

\ [\ begin {alineado}
\ left (\ cos\ left (\ alpha_ {0}\ right) -\ cos\ left (\ beta_ {0}\ right)\ right) ^ {2} +\ left (\ sin\ left (\ alpha_ {0}\ right) -\ sin\ left (\ beta_ {0}\ right)\ right) ^ {2} =& cos {^ ^ 2}\ izquierda (\ alpha_ {0}\ derecha) -2\ cos\ izquierda (\ alpha_ {0}\ derecha)\ cos\ izquierda (\ beta_ {0}\ derecha) +\ cos ^ {2}\ izquierda (\ beta_ {0}\ derecha)\\
&+\ sin ^ {2}\ izquierda (\ alpha_ {0}\ derecha) -2\ sin\ izquierda (\ alpha_ {0}\ derecha)\ sin\ izquierda (\ beta_ {0}\ derecha) +\ sin ^ {2}\ izquierda (\ beta_ {0}\ derecha)\\
=&\ cos ^ {2}\ izquierda (\ alpha_ {0}\ derecha) +\ sin ^ {2}\ izquierda (\ alpha_ {0}\ derecha) +\ cos ^ {2}\ izquierda (\ beta_ {0}\ derecha) +\ sin ^ {2}\ izquierda (\ beta_ {0}\ derecha)\\
&-2\ cos\ izquierda (\ alpha_ {0}\ derecha)\ cos\ izquierda (\ beta_ {0}\ derecha) -2\ sin\ izquierda (\ alpha_ {0}\ derecha)\ sin\ izquierda (\ beta_ {0}\ derecha)
\ end {alineada}\ nonumber\]

De las identidades pitagóricas,\(\cos^2(\alpha_0) + \sin^2(\alpha_0) = 1\) y\(\cos^2(\beta_0) + \sin^2(\beta_0) = 1\), así

\[\left(\cos \left(\alpha_{0}\right)-\cos \left(\beta_{0}\right)\right)^{2}+\left(\sin \left(\alpha_{0}\right)-\sin \left(\beta_{0}\right)\right)^{2}=2-2 \cos \left(\alpha_{0}\right) \cos \left(\beta_{0}\right)-2 \sin \left(\alpha_{0}\right) \sin \left(\beta_{0}\right)\nonumber\]

Volviendo nuestra atención hacia el lado derecho de nuestra ecuación, encontramos

\ [\ begin {alineado}
\ izquierda (\ cos\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha) -1\ derecha) ^ {2} +\ izquierda (\ sin\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha) -0\ derecha) ^ {2} &=\ cos ^ {2}\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha) -2\ cos\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha) +1+\ sin ^ {2}\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha)\\
&=1+\ cos ^ {2}\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha) +\ sin ^ {2}\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha) -2\ cos\ izquierda (\ alpha_ {0} -\ beta_ {0}\ derecha)
\ final {alineado}\ nonumber\]

Una vez más, simplificamos\(\cos^2(\alpha_0 - \beta_0) + \sin^2(\alpha_0 - \beta_0)= 1\), para que

\[\left(\cos \left(\alpha_{0}-\beta_{0}\right)-1\right)^{2}+\left(\sin \left(\alpha_{0}-\beta_{0}\right)-0\right)^{2}=2-2 \cos \left(\alpha_{0}-\beta_{0}\right)\nonumber\]

Poniéndolo todo junto, obtenemos\(2 - 2\cos(\alpha_0)\cos(\beta_0) - 2\sin(\alpha_0)\sin(\beta_0) = 2 - 2\cos(\alpha_0 - \beta_0)\), lo que simplifica a:\(\cos(\alpha_0 - \beta_0) = \cos(\alpha_0)\cos(\beta_0) + \sin(\alpha_0)\sin(\beta_0)\). Desde\(\alpha\) y\(\alpha_0\),\(\beta\) y\(\beta_0\) y\(\alpha - \beta\) y\(\alpha_0- \beta_0\) son todos pares coterminales de ángulos, tenemos\(\cos(\alpha - \beta) = \cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta)\). Para el caso donde\(\alpha_0 \leq \beta_0\), podemos aplicar el argumento anterior al ángulo\(\beta_0 - \alpha_0\) para obtener la identidad\(\cos(\beta_0 - \alpha_0) = \cos(\beta_0)\cos(\alpha_0) + \sin(\beta_0)\sin(\alpha_0)\). Aplicando la Identidad Incluso del coseno, obtenemos\(\cos(\beta_0 - \alpha_0) = \cos( - (\alpha_0 - \beta_0)) = \cos(\alpha_0 - \beta_0)\), y obtenemos la identidad en este caso, también.

Para obtener la identidad de suma para el coseno, usamos la fórmula de diferencia junto con las identidades pares/impares

\[\cos (\alpha+\beta)=\cos (\alpha-(-\beta))=\cos (\alpha) \cos (-\beta)+\sin (\alpha) \sin (-\beta)=\cos (\alpha) \cos (\beta)-\sin (\alpha) \sin (\beta)\nonumber\]

Ponemos a buen uso estas nuevas identidades en el siguiente ejemplo.

Ejemplo 10.4.1

1. Encuentra el valor exacto de\(\cos\left(15^{\circ}\right)\).
2. Verificar la identidad:\(\cos\left(\frac{\pi}{2} - \theta\right) = \sin(\theta)\).

Solución

1. Para poder utilizar el Teorema 10.13 para encontrar\(\cos\left(15^{\circ}\right)\), necesitamos escribir\(15^{\circ}\) como una suma o diferencia de ángulos cuyos cosenos y senos conocemos. Una forma de hacerlo es escribir\(15^{\circ} = 45^{\circ} - 30^{\circ}\).

   \[\begin{array}{rcl} \cos\left(15^{\circ}\right) & = & \cos\left(45^{\circ} - 30^{\circ} \right) \\[4pt] & = & \cos\left(45^{\circ}\right)\cos\left(30^{\circ} \right) + \sin\left(45^{\circ}\right)\sin\left(30^{\circ} \right) \\[4pt] & = & \left( \dfrac{\sqrt{2}}{2} \right)\left( \dfrac{\sqrt{3}}{2} \right) + \left( \dfrac{\sqrt{2}}{2} \right)\left( \dfrac{1}{2} \right)\\[15pt] & = & \dfrac{\sqrt{6}+ \sqrt{2}}{4} \\ \end{array}\nonumber\]

2. En una aplicación sencilla del Teorema 10.13, encontramos

   \[\begin{array}{rcl} \cos\left(\dfrac{\pi}{2} - \theta\right) & = & \cos\left(\dfrac{\pi}{2}\right)\cos\left(\theta\right) + \sin\left(\dfrac{\pi}{2}\right)\sin\left(\theta \right) \\ [10pt] & = & \left( 0 \right)\left( \cos(\theta) \right) + \left( 1 \right)\left( \sin(\theta) \right) \\ [4pt] & = & \sin(\theta) \\ \end{array}\nonumber\]

La identidad verificada en el Ejemplo 10.4.1, es decir,\(\cos\left(\frac{\pi}{2} - \theta\right) = \sin(\theta)\), es la primera de las célebres identidades de 'cofunción'. Estas identidades fueron insinuadas por primera vez en el Ejercicio 74 de la Sección 10.2. De\(\sin(\theta) = \cos\left(\frac{\pi}{2} - \theta\right)\), obtenemos:

\[\sin\left(\dfrac{\pi}{2} - \theta\right) = \cos\left(\dfrac{\pi}{2} -\left[\dfrac{\pi}{2} - \theta\right]\right) = \cos(\theta),\nonumber\]

que dice, en palabras, que el 'co'seno de un ángulo es el seno de su 'co'mplement. Ahora que estas identidades se han establecido para el coseno y el seno, las funciones circulares restantes siguen su ejemplo. Las pruebas restantes se dejan como ejercicios.

Teorema 10.14. Identidades de cofunción

Para todos los ángulos aplicables\(\theta\),

• \(\cos\left(\dfrac{\pi}{2} - \theta \right) = \sin(\theta)\)
• \(\sin\left(\dfrac{\pi}{2} - \theta \right) = \cos(\theta)\)
• \(\sec\left(\dfrac{\pi}{2} - \theta \right) = \csc(\theta)\)
• \(\csc\left(\dfrac{\pi}{2} - \theta \right) = \sec(\theta)\)
• \(\tan\left(\dfrac{\pi}{2} - \theta \right) = \cot(\theta)\)
• \(\cot\left(\dfrac{\pi}{2} - \theta \right) = \tan(\theta)\)

Con las Identidades de Cofunción en su lugar, ahora estamos en la posición de derivar las fórmulas de suma y diferencia para seno. Para derivar la fórmula de suma para seno, convertimos a cosenos usando una identidad de cofunción, luego expandimos usando la fórmula de diferencia para coseno

\[\begin{array}{rcl} \sin(\alpha + \beta) & = & \cos\left( \dfrac{\pi}{2} - (\alpha + \beta) \right) \\ [10pt] & = & \cos\left( \left[\dfrac{\pi}{2} - \alpha \right] - \beta \right) \\ [10pt] & = & \cos\left(\dfrac{\pi}{2} - \alpha \right) \cos(\beta) + \sin\left(\dfrac{\pi}{2} - \alpha \right)\sin(\beta) \\ [10pt] & = & \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta) \\ \end{array}\nonumber\]

Podemos derivar la fórmula de diferencia para seno reescribiendo\(\sin(\alpha - \beta)\) como\(\sin(\alpha + (-\beta))\) y usando la fórmula suma y las identidades pares/impares. Nuevamente, dejamos los detalles al lector.

Teorema 10.15. Identidades de suma y diferencia para seno

Para todos los ángulos\(\alpha\) y\(\beta\),

• \(\sin(\alpha + \beta) = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta)\)
• \(\sin(\alpha - \beta) = \sin(\alpha) \cos(\beta) - \cos(\alpha) \sin(\beta)\)

Ejemplo 10.4.2

1. Encuentra el valor exacto de\(\sin\left(\frac{19 \pi}{12}\right)\)
2. Si\(\alpha\) es un ángulo del Cuadrante II con\(\sin(\alpha) = \frac{5}{13}\), y\(\beta\) es un ángulo del Cuadrante III con\(\tan(\beta) = 2\), encontrar\(\sin(\alpha - \beta)\).
3. Derivar una fórmula para\(\tan(\alpha + \beta)\) en términos de\(\tan(\alpha)\) y\(\tan(\beta)\).

Solución.

1. Al igual que en el Ejemplo 10.4.1, necesitamos escribir el ángulo\(\frac{19 \pi}{12}\) como una suma o diferencia de ángulos comunes. El denominador de\(12\) sugiere una combinación de ángulos con denominadores\(3\) y\(4\). Una de esas combinaciones es\(\; \frac{19 \pi}{12} = \frac{4 \pi}{3} + \frac{\pi}{4}\). Aplicando el Teorema 10.15, obtenemos

   \[\begin{array}{rcl} \sin\left(\dfrac{19 \pi}{12}\right) & = & \sin\left(\dfrac{4 \pi}{3} + \dfrac{\pi}{4} \right) \\ [10pt] & = & \sin\left(\dfrac{4 \pi}{3} \right)\cos\left(\dfrac{\pi}{4} \right) + \cos\left(\dfrac{4 \pi}{3} \right)\sin\left(\dfrac{\pi}{4} \right) \\ [10pt] & = & \left( -\dfrac{\sqrt{3}}{2} \right)\left( \dfrac{\sqrt{2}}{2} \right) + \left( -\dfrac{1}{2} \right)\left( \dfrac{\sqrt{2}}{2} \right) \\[15pt] & = & \dfrac{-\sqrt{6}- \sqrt{2}}{4} \\ \end{array}\nonumber\]

2. Para poder encontrar\(\sin(\alpha - \beta)\) usando el Teorema 10.15, necesitamos encontrar\(\cos(\alpha)\) y ambos\(\cos(\beta)\) y\(\sin(\beta)\). Para encontrar\(\cos(\alpha)\), utilizamos la Identidad Pitagórica\(\cos^2(\alpha) + \sin^2(\alpha) = 1\). Ya que\(\sin(\alpha) = \frac{5}{13}\), tenemos\(\cos^{2}(\alpha) + \left(\frac{5}{13}\right)^2 = 1\), o\(\cos(\alpha) = \pm \frac{12}{13}\). Ya que\(\alpha\) es un ángulo Cuadrante II,\(\cos(\alpha) = -\frac{12}{13}\). Ahora nos pusimos a encontrar\(\cos(\beta)\) y\(\sin(\beta)\). Tenemos varias formas de proceder, pero la Identidad Pitagórica\(1 + \tan^{2}(\beta) = \sec^{2}(\beta)\) es una forma rápida de obtener\(\sec(\beta)\), y por lo tanto,,\(\cos(\beta)\). Con\(\tan(\beta) = 2\), conseguimos\(1 + 2^2 = \sec^{2}(\beta)\) así que\(\sec(\beta) = \pm \sqrt{5}\). Ya que\(\beta\) es un ángulo Cuadrante III,\(\sec(\beta) = -\sqrt{5}\) así lo elegimos\(\cos(\beta) = \frac{1}{\sec(\beta)} = \frac{1}{-\sqrt{5}} = -\frac{\sqrt{5}}{5}\). Ahora tenemos que determinar\(\sin(\beta)\). Podríamos usar La identidad pitagórica\(\cos^{2}(\beta) + \sin^{2}(\beta) = 1\), pero optamos en su lugar por usar una identidad de cociente. De\(\tan(\beta) = \frac{\sin(\beta)}{\cos(\beta)}\), tenemos\(\sin(\beta) = \tan(\beta) \cos(\beta)\) así que conseguimos\(\sin(\beta) = (2) \left( -\frac{\sqrt{5}}{5}\right) = - \frac{2 \sqrt{5}}{5}\). Ahora tenemos todas las piezas necesarias para encontrar\(\sin(\alpha - \beta)\):

   \[\begin{array}{rcl} \sin(\alpha - \beta) & = & \sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta) \\ & = & \left( \dfrac{5}{13} \right)\left( -\dfrac{\sqrt{5}}{5} \right) - \left( -\dfrac{12}{13} \right)\left( - \dfrac{2 \sqrt{5}}{5} \right) \\ & = & -\dfrac{29\sqrt{5}}{65} \\ \end{array}\nonumber\]

3. Podemos comenzar a expandirnos\(\tan(\alpha + \beta)\) usando una identidad de cociente y nuestras fórmulas de suma

   \[\begin{array}{rcl} \tan(\alpha + \beta) & = & \dfrac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} \\ [10pt] & = & \dfrac{\sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)} \\ \end{array}\nonumber\]

   Desde\(\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}\) y\(\tan(\beta) = \frac{\sin(\beta)}{\cos(\beta)}\), parece como si dividiéramos tanto el numerador como el denominador por\(\cos(\alpha) \cos(\beta)\) vamos a tener lo que queremos

   \[\begin{array}{rcl} \tan(\alpha + \beta) & = & \dfrac{\sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)} \cdot\dfrac{\dfrac{1}{\cos(\alpha) \cos(\beta)}}{\dfrac{1}{\cos(\alpha) \cos(\beta)}}\\ & & \\ & = & \dfrac{\dfrac{\sin(\alpha) \cos(\beta)}{\cos(\alpha) \cos(\beta)} + \dfrac{\cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}}{\dfrac{\cos(\alpha) \cos(\beta)}{\cos(\alpha) \cos(\beta)} - \dfrac{\sin(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}}\\ & & \\ & = & \dfrac{\dfrac{\sin(\alpha) \cancel{\cos(\beta)}}{\cos(\alpha) \cancel{\cos(\beta)}} + \dfrac{\cancel{\cos(\alpha)} \sin(\beta)}{\cancel{\cos(\alpha)} \cos(\beta)}}{\dfrac{\cancel{\cos(\alpha)} \cancel{\cos(\beta)}}{\cancel{\cos(\alpha)} \cancel{\cos(\beta)}} - \dfrac{\sin(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}}\\ & & \\ & = & \dfrac{\tan(\alpha) + \tan(\beta)}{1 -\tan(\alpha) \tan(\beta)}\\ \end{array}\nonumber\]

   Naturalmente, esta fórmula se limita a aquellos casos en los que se definen todas las tangentes.

La fórmula desarrollada en el Ejercicio 10.4.2 para se\(\tan(\alpha + \beta)\) puede utilizar para encontrar una fórmula para\(\tan(\alpha - \beta)\) reescribiendo la diferencia como suma\(\tan(\alpha + (-\beta))\), y se anima al lector a rellenar los detalles. A continuación resumimos todas las fórmulas de suma y diferencia para coseno, seno y tangente.

Teorema 10.16. Identidades de suma y diferencia

Para todos los ángulos aplicables\(\alpha\) y\(\beta\),

• \(\cos(\alpha \pm \beta) = \cos(\alpha) \cos(\beta) \mp \sin(\alpha) \sin(\beta)\)
• \(\sin(\alpha \pm \beta) = \sin(\alpha) \cos(\beta) \pm \cos(\alpha) \sin(\beta)\)
• \(\tan(\alpha \pm \beta) = \dfrac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha) \tan(\beta)}\)

En el enunciado del Teorema 10.16, hemos combinado los casos para la suma '\(+\)' y diferencia '\(-\)' de ángulos en una sola fórmula. La convención aquí es que si quieres la fórmula para la suma '\(+\)' de dos ángulos, usas el signo superior en la fórmula; para la diferencia, '\(-\)', usa el signo inferior. Por ejemplo,\[\tan(\alpha - \beta) = \dfrac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \tan(\beta)}\nonumber\]

Si especializamos las fórmulas de suma en el Teorema 10.16 al caso cuando\(\alpha = \beta\), obtenemos las siguientes Identidades de 'Doble Angle'.

Teorema 10.17. Identidades de doble ángulo

Para todos los ángulos aplicables\(\theta\),

• \(\cos(2\theta) = \left\{ \begin{array}{l} \cos^{2}(\theta) - \sin^{2}(\theta)\\[4pt] 2\cos^{2}(\theta) - 1 \\[4pt] 1-2\sin^{2}(\theta) \end{array} \right.\)
• \(\sin(2\theta) = 2\sin(\theta)\cos(\theta)\)
• \(\tan(2\theta) = \dfrac{2\tan(\theta)}{1 - \tan^{2}(\theta)}\)

Las tres formas diferentes para\(\cos(2\theta)\) pueden explicarse por nuestra capacidad de 'intercambiar' cuadrados de coseno y seno a través de la Identidad Pitagórica\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\) y dejamos los detalles al lector. Es interesante señalar que para determinar el valor de\(\cos(2\theta)\), solo se requiere una pieza de información: cualquiera\(\cos(\theta)\) o\(\sin(\theta)\). Para determinar\(\sin(2\theta)\), sin embargo, parece que debemos conocer ambos\(\sin(\theta)\) y\(\cos(\theta)\). En el siguiente ejemplo, mostramos cómo podemos encontrar\(\sin(2\theta)\) conociendo solo una pieza de información, a saber\(\tan(\theta)\).

Ejemplo 10.4.3

1. Supongamos que\(P(-3,4)\) se encuentra en el lado terminal de\(\theta\) cuando\(\theta\) se traza en posición estándar. Encuentre\(\cos(2\theta)\)\(\sin(2\theta)\) y determine el cuadrante en el que se\(2\theta\) encuentra el lado terminal del ángulo cuando se traza en posición estándar.
2. Si es\(\sin(\theta) = x\) por\(-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\), encuentra una expresión para\(\sin(2\theta)\) en términos de\(x\).
3. [doubleanglesinewtan] Verificar la identidad:\(\sin(2\theta) = \dfrac{2\tan(\theta)}{1 + \tan^{2}(\theta)}\).
4. Expresar\(\cos(3\theta)\) como polinomio en términos de\(\cos(\theta)\).

Solución.

1. Usando el Teorema 10.3 de la Sección 10.2 con\(x = -3\) y\(y=4\), nos encontramos\(r = \sqrt{x^2+y^2} = 5\). De ahí,\(\cos(\theta) = -\frac{3}{5}\) y\(\sin(\theta) = \frac{4}{5}\). Aplicando el Teorema 10.17, obtenemos\(\cos(2\theta) = \cos^{2}(\theta) - \sin^{2}(\theta) = \left(-\frac{3}{5}\right)^2 - \left(\frac{4}{5}\right)^2 = -\frac{7}{25}\), y\(\sin(2\theta) = 2 \sin(\theta) \cos(\theta) = 2 \left(\frac{4}{5}\right)\left(-\frac{3}{5}\right) = -\frac{24}{25}\). Dado que tanto el coseno como el seno de\(2\theta\) son negativos, el lado terminal de\(2\theta\), cuando se traza en posición estándar, se encuentra en el Cuadrante III.
2. Si tu primera reacción a '\(\sin(\theta) = x\)' es 'No, ¡no lo es\(\cos(\theta) = x\)! ' entonces efectivamente has aprendido algo, y nos consolamos en eso. Sin embargo, el contexto lo es todo. Aquí, '\(x\)' es solo una variable - no necesariamente representa la\(x\) -coordenada del punto en El Círculo de Unidad que se encuentra en el lado terminal de\(\theta\), suponiendo que\(\theta\) se dibuja en posición estándar. Aquí,\(x\) representa la cantidad\(\sin(\theta)\), y lo que deseamos saber es cómo expresarnos\(\sin(2\theta)\) en términos de\(x\). Veremos más de este tipo de cosas en la Sección 10.6, y, como siempre, esto es algo que necesitamos para Cálculo. Ya que\(\sin(2\theta) = 2 \sin(\theta) \cos(\theta)\), necesitamos escribir\(\cos(\theta)\) en términos de\(x\) para terminar el problema. Sustituimos\(x = \sin(\theta)\) en la Identidad Pitagórica,\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\), para obtener\(\cos^{2}(\theta) + x^2 = 1\), o\(\cos(\theta) = \pm \sqrt{1-x^2}\). Desde\(-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\),\(\cos(\theta) \geq 0\), y así\(\cos(\theta) = \sqrt{1-x^2}\). Nuestra respuesta final es\(\sin(2\theta) = 2 \sin(\theta) \cos(\theta) = 2x\sqrt{1-x^2}\).
3. Empezamos por el lado derecho de la identidad y señalamos eso\(1 + \tan^{2}(\theta) = \sec^{2}(\theta)\). A partir de este punto, utilizamos las Identidades Recíprocas y Cocientes para reescribir\(\tan(\theta)\) y\(\sec(\theta)\) en términos de\(\cos(\theta)\) y\(\sin(\theta)\):

   \[\begin{array}{rcl} \dfrac{2\tan(\theta)}{1 + \tan^{2}(\theta)} & = & \dfrac{2\tan(\theta)}{\sec^{2}(\theta)}= \dfrac{2 \left( \dfrac{\sin(\theta)}{\cos(\theta)}\right)}{\dfrac{1}{\cos^{2}(\theta)}}= 2\left( \dfrac{\sin(\theta)}{\cos(\theta)}\right) \cos^{2}(\theta) \\[15pt] & = & 2\left( \dfrac{\sin(\theta)}{\cancel{\cos(\theta)}}\right) \cancel{\cos(\theta)} \cos(\theta) = 2\sin(\theta) \cos(\theta) = \sin(2\theta) \\ \end{array}\nonumber\]

4. En el Teorema 10.17, una de las fórmulas para\(\cos(2\theta)\), es decir\(\cos(2\theta) = 2\cos^{2}(\theta) - 1\),\(\cos(2\theta)\) se expresa como un polinomio en términos de\(\cos(\theta)\). Ahora se nos pide encontrar tal identidad para\(\cos(3\theta)\). Usando la fórmula de suma para coseno, comenzamos con

   \[\begin{array}{rcl} \cos(3\theta) & = & \cos(2\theta + \theta) \\[4pt] & = & \cos(2\theta)\cos(\theta) - \sin(2\theta)\sin(\theta) \\ \end{array}\nonumber\]

   Nuestro objetivo final es expresar el lado derecho en términos de\(\cos(\theta)\) solo. Sustituimos\(\cos(2\theta) = 2\cos^{2}(\theta) -1\) y\(\sin(2\theta) = 2\sin(\theta)\cos(\theta)\) qué rendimientos

   \[\begin{array}{rcl} \cos(3\theta) & = & \cos(2\theta)\cos(\theta) - \sin(2\theta)\sin(\theta) \\[4pt] & = & \left(2\cos^{2}(\theta) - 1\right) \cos(\theta) - \left(2 \sin(\theta) \cos(\theta) \right)\sin(\theta) \\[4pt] & = & 2\cos^{3}(\theta)- \cos(\theta) - 2 \sin^2(\theta) \cos(\theta) \\ \end{array}\nonumber\]

   Finalmente, intercambiamos\(\sin^{2}(\theta)\) por\(1 - \cos^{2}(\theta)\) cortesía de la Identidad Pitagórica, y obtenemos

   \[\begin{array}{rcl} \cos(3\theta) & = & 2\cos^{3}(\theta)- \cos(\theta) - 2 \sin^2(\theta) \cos(\theta) \\[4pt] & = & 2\cos^{3}(\theta)- \cos(\theta) - 2 \left(1 - \cos^{2}(\theta)\right) \cos(\theta) \\[4pt] & = & 2\cos^{3}(\theta)- \cos(\theta) - 2\cos(\theta) + 2\cos^{3}(\theta) \\[4pt] & = & 4\cos^{3}(\theta)- 3\cos(\theta) \\ \end{array}\nonumber\]y ya terminamos.

En el último problema del Ejemplo 10.4.3, vimos como podíamos reescribir\(\cos(3\theta)\) como sumas de poderes de\(\cos(\theta)\). En Cálculo, tenemos ocasión de hacer lo contrario; es decir, reducir el poder del coseno y del seno. Resolver la identidad\(\cos(2\theta) = 2\cos^{2}(\theta) -1\)\(\cos^{2}(\theta)\) y la identidad\(\cos(2\theta) = 1 - 2\sin^{2}(\theta)\) para\(\sin^{2}(\theta)\) los resultados en las fórmulas acertadamente llamadas 'Reducción de potencia' a continuación.

Teorema 10.18. Fórmulas para la reducción

Para todos los ángulos\(\theta\),

• \(\cos^{2}(\theta) = \dfrac{1 + \cos(2\theta)}{2}\)
• \(\sin^{2}(\theta) = \dfrac{1 - \cos(2\theta)}{2}\)

Ejemplo 10.4.4

Reescribir\(\sin ^{2}(\theta) \cos ^{2}(\theta)\) como suma y diferencia de cosenos a la primera potencia.

Solución

Comenzamos con una aplicación directa del Teorema 10.18

\[\begin{array}{rcl} \sin^{2}(\theta) \cos^{2}(\theta) & = & \left( \dfrac{1 - \cos(2\theta)}{2} \right) \left( \dfrac{1 + \cos(2\theta)}{2} \right) \\ [10pt] & = & \dfrac{1}{4}\left(1 - \cos^{2}(2\theta)\right) \\ [10pt] & = & \dfrac{1}{4} - \dfrac{1}{4}\cos^{2}(2\theta) \\ \end{array}\nonumber\]

A continuación, aplicamos la fórmula de reducción de potencia\(\cos^{2}(2\theta)\) para terminar la reducción

\[\begin{array}{rcl} \sin^{2}(\theta) \cos^{2}(\theta) & = & \dfrac{1}{4} - \dfrac{1}{4}\cos^{2}(2\theta) \\ [10pt] & = & \dfrac{1}{4} - \dfrac{1}{4} \left(\dfrac{1 + \cos(2(2\theta))}{2}\right) \\ [10pt] & = & \dfrac{1}{4} - \dfrac{1}{8} - \dfrac{1}{8}\cos(4\theta) \\ [10pt] & = & \dfrac{1}{8} - \dfrac{1}{8}\cos(4\theta) \\ \end{array}\nonumber\]

Otra aplicación de las fórmulas de reducción de potencia son las fórmulas de medio ángulo. Para comenzar, aplicamos la Fórmula de Reducción de Potencia a\(\cos^{2}\left(\frac{\theta}{2}\right)\)

\[\cos^{2}\left(\dfrac{\theta}{2}\right) = \dfrac{1 + \cos\left(2 \left(\frac{\theta}{2}\right)\right)}{2} = \dfrac{1 + \cos(\theta)}{2}.\nonumber\]

Podemos obtener una fórmula para\(\cos\left(\frac{\theta}{2}\right)\) mediante la extracción de raíces cuadradas. De manera similar, podemos obtener una fórmula de medio ángulo para seno, y usando una fórmula de cociente, obtener una fórmula de medio ángulo para tangente. Resumimos estas fórmulas a continuación.

Teorema 10.19. Fórmulas de ángulo medio

Para todos los ángulos aplicables\(\theta\),

• \(\cos\left(\dfrac{\theta}{2}\right) = \pm \sqrt{\dfrac{1 + \cos(\theta)}{2}}\)
• \(\sin\left(\dfrac{\theta}{2}\right) = \pm \sqrt{\dfrac{1 - \cos(\theta)}{2}}\)
• \(\tan\left(\dfrac{\theta}{2}\right) = \pm \sqrt{\dfrac{1 - \cos(\theta)}{1+\cos(\theta)}}\)

donde la elección de\(\pm\) depende del cuadrante en el que se\(\dfrac{\theta}{2}\) encuentra el lado terminal de.

Ejemplo 10.4.5

1. Utilice una fórmula de medio ángulo para encontrar el valor exacto de\(\cos\left(15^{\circ}\right)\).
2. Supongamos\(-\pi \leq \theta \leq 0\) con\(\cos(\theta) = -\frac{3}{5}\). Encuentra\(\sin\left(\frac{\theta}{2}\right)\).
3. Usar la identidad dada en el número 3 del Ejemplo 10.4.3 para derivar la identidad\[\tan\left(\dfrac{\theta}{2}\right) = \dfrac{\sin(\theta)}{1+\cos(\theta)}\nonumber\]

Solución

1. Para utilizar la fórmula de medio ángulo, observamos que\(15^{\circ} = \frac{30^{\circ}}{2}\) y como\(15^{\circ}\) es un ángulo del Cuadrante I, su coseno es positivo. Así tenemos

   \[\begin{array}{rcl} \cos\left(15^{\circ}\right) & = & + \sqrt{\dfrac{1+\cos\left(30^{\circ}\right)}{2}} = \sqrt{\dfrac{1+\frac{\sqrt{3}}{2}}{2}}\\ [10pt] & = & \sqrt{\dfrac{1+\frac{\sqrt{3}}{2}}{2}\cdot \dfrac{2}{2}} = \sqrt{\dfrac{2+\sqrt{3}}{4}} = \dfrac{\sqrt{2+\sqrt{3}}}{2}\\ \end{array}\nonumber\]

   De vuelta en el Ejemplo 10.4.1, encontramos\(\cos\left(15^{\circ}\right)\) usando la fórmula de diferencia para coseno. En ese caso, lo determinamos\(\cos\left(15^{\circ}\right) = \frac{\sqrt{6}+ \sqrt{2}}{4}\). Se anima al lector a demostrar que estas dos expresiones son iguales.

2. Si\(-\pi \leq \theta \leq 0\), entonces\(-\frac{\pi}{2} \leq \frac{\theta}{2} \leq 0\), lo que significa\(\sin\left(\frac{\theta}{2}\right) < 0\). Teorema 10.19 da

   \[\begin{array}{rcl} \sin\left(\dfrac{\theta}{2} \right) & = & -\sqrt{\dfrac{1-\cos\left(\theta \right)}{2}} = -\sqrt{\dfrac{1- \left(-\frac{3}{5}\right)}{2}}\\ [10pt] & = & -\sqrt{\dfrac{1 + \frac{3}{5}}{2} \cdot \dfrac{5}{5}} = -\sqrt{\dfrac{8}{10}} = -\dfrac{2\sqrt{5}}{5}\\ \end{array}\nonumber\]

3. En lugar de nuestro enfoque habitual para verificar identidades, es decir, comenzando por un lado de la ecuación y tratando de transformarlo en el otro, comenzaremos con la identidad que probamos en el número 3 del Ejemplo 10.4.3 y la manipularemos en la identidad que se nos pide probar. La identidad con la que se nos pide empezar es\(\; \sin(2\theta) = \frac{2\tan(\theta)}{1 + \tan^{2}(\theta)}\). Si vamos a usar esto para derivar una identidad para\(\tan\left(\frac{\theta}{2}\right)\), parece razonable proceder reemplazando cada ocurrencia\(\theta\) de por\(\frac{\theta}{2}\)

   \[\begin{array}{rcl} \sin\left(2 \left(\frac{\theta}{2}\right)\right) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{1 + \tan^{2}\left(\frac{\theta}{2}\right)} \\[15pt] \sin(\theta) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{1 + \tan^{2}\left(\frac{\theta}{2}\right)} \\ \end{array}\nonumber\]

   Ahora tenemos lo que\(\sin(\theta)\) necesitamos, pero de alguna manera necesitamos obtener un factor de\(1+\cos(\theta)\) participación. Para involucrar a los cosenos, recuérdalo\(1 + \tan^{2}\left(\frac{\theta}{2}\right) = \sec^{2}\left(\frac{\theta}{2}\right)\). Seguimos manipulando nuestra identidad dada convirtiendo las secantes en cosenos y usando una fórmula de reducción de potencia

   \[\begin{array}{rcl} \sin(\theta) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{1 + \tan^{2}\left(\frac{\theta}{2}\right)} \\[15pt] \sin(\theta) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{\sec^{2}\left(\frac{\theta}{2}\right)} \\[15pt] \sin(\theta) & = & 2 \tan\left(\frac{\theta}{2}\right) \cos^{2}\left(\frac{\theta}{2}\right) \\[4pt] \sin(\theta) & = & 2 \tan\left(\frac{\theta}{2}\right) \left(\dfrac{1 + \cos\left(2 \left(\frac{\theta}{2}\right)\right)}{2}\right) \\[15pt] \sin(\theta) & = & \tan\left(\frac{\theta}{2}\right) \left(1+\cos(\theta) \right) \\[4pt] \tan\left(\dfrac{\theta}{2}\right) & = & \dfrac{\sin(\theta)}{1+\cos(\theta)} \\ \end{array}\nonumber\]

Nuestro siguiente lote de identidades, las Fórmulas de Producto a Suma, ³ se verifican fácilmente expandiendo cada uno de los lados de la mano derecha de acuerdo con el Teorema 10.16 y como debe esperar a estas alturas dejamos los detalles como ejercicios. Son de particular uso en Cálculo, y los enumeramos aquí como referencia.

Teorema 10.20. Fórmulas de producto a suma

Para todos los ángulos\(\alpha\) y\(\beta\),

• \(\cos(\alpha)\cos(\beta) = \frac{1}{2} \left[ \cos(\alpha - \beta) + \cos(\alpha + \beta)\right]\)
• \(\sin(\alpha)\sin(\beta) = \frac{1}{2} \left[ \cos(\alpha - \beta) - \cos(\alpha + \beta)\right]\)
• \(\sin(\alpha)\cos(\beta) = \frac{1}{2} \left[ \sin(\alpha - \beta) + \sin(\alpha + \beta)\right]\)

Relacionadas con las Fórmulas de Producto a Suma son las Fórmulas Suma a Producto, que tendremos necesidad de en la Sección 10.7. Estos se verifican fácilmente usando las fórmulas de producto para sumar, y como tal, sus pruebas se dejan como ejercicios.

Teorema 10.21. Suma a Producto Formulastoproducto

Para todos los ángulos\(\alpha\) y\(\beta\),

• \(\cos(\alpha) + \cos(\beta) = 2 \cos\left( \dfrac{\alpha + \beta}{2}\right)\cos\left( \dfrac{\alpha - \beta}{2}\right)\)
• \(\cos(\alpha) - \cos(\beta) = - 2 \sin\left( \dfrac{\alpha + \beta}{2}\right)\sin\left( \dfrac{\alpha - \beta}{2}\right)\)
• \(\sin(\alpha) \pm \sin(\beta) = 2 \sin\left( \dfrac{\alpha \pm \beta}{2}\right)\cos\left( \dfrac{\alpha \mp \beta}{2}\right)\)

Ejemplo 10.4.6

1. Escribir\(\; \cos(2\theta)\cos(6\theta) \;\) como suma.
2. Escribir\(\; \sin(\theta) - \sin(3\theta) \;\) como producto.

Solución.

1. Identificando\(\alpha = 2\theta\) y\(\beta = 6\theta\), encontramos

   \[\begin{array}{rcl} \cos(2\theta)\cos(6\theta) & = & \frac{1}{2} \left[ \cos(2\theta - 6\theta) + \cos(2\theta + 6\theta)\right]\\ [4pt] & = & \frac{1}{2} \cos(-4\theta) + \frac{1}{2}\cos(8\theta) \\ [4pt] & = & \frac{1}{2} \cos(4\theta) + \frac{1}{2} \cos(8\theta), \end{array}\nonumber\]donde la última igualdad es cortesía de la identidad par para el coseno,\(\cos(-4\theta) = \cos(4\theta)\).

2. Identificación\(\alpha = \theta\) y\(\beta = 3\theta\) rendimientos

   \[\begin{array}{rcl} \sin(\theta) - \sin(3\theta) & = & 2 \sin\left( \dfrac{\theta - 3\theta}{2}\right)\cos\left( \dfrac{\theta + 3\theta}{2}\right) \\[4pt] & = & 2 \sin\left( -\theta \right)\cos\left( 2\theta \right) \\[4pt] & = & -2 \sin\left( \theta \right)\cos\left( 2\theta \right), \\ \end{array}\nonumber\]donde la última igualdad es cortesía de la extraña identidad para seno,\(\sin(-\theta) = -\sin(\theta)\).

Se recuerda al lector que todas las identidades presentadas en esta sección que consideran las funciones circulares como funciones de ángulos (en medida radianes) se aplican igualmente bien a las funciones circulares (trigonométricas) consideradas como funciones de números reales. En los Ejercicios 38 - 43 de la Sección 10.5, vemos cómo algunas de estas identidades se manifiestan geométricamente a medida que estudiamos las gráficas de estas funciones. En los próximos Ejercicios, sin embargo, necesitas hacer todo tu trabajo analíticamente sin gráficas.

10.4.1. Ejercicios

En los Ejercicios 1 - 6, utilice las Identidades Pares/Impares para verificar la identidad. Supongamos que todas las cantidades están definidas.

1. \(\sin(3\pi - 2\theta) = -\sin(2\theta - 3\pi)\)
2. \(\cos \left( -\dfrac{\pi}{4} - 5t \right) = \cos \left( 5t + \dfrac{\pi}{4} \right)\)
3. \(\tan(-t^{2} + 1) = -\tan(t^{2} - 1)\)
4. \(\csc(-\theta - 5) = -\csc(\theta + 5)\)
5. \(\sec(-6t) = \sec(6t)\)
6. \(\cot(9 - 7\theta) = -\cot(7\theta - 9)\)

En los Ejercicios 7 - 21, usa las Identidades Suma y Diferencia para encontrar el valor exacto. Es posible que también tengas necesidad del Cociente, Recíproco o Identidades Pares/Impares.

7. \(\cos(75^{\circ})\)
8. \(\sec(165^{\circ})\)
9. \(\sin(105^{\circ})\)
10. \(\csc(195^{\circ})\)
11. \(\cot(255^{\circ})\)
12. \(\tan(375^{\circ})\)
13. \(\cos\left(\dfrac{13\pi}{12}\right)\)
14. \(\sin\left(\dfrac{11\pi}{12}\right)\)
15. \(\tan\left(\dfrac{13\pi}{12}\right)\)
16. [cos7pi12]\(\cos \left( \dfrac{7\pi}{12} \right)\)
17. \(\tan \left( \dfrac{17\pi}{12} \right)\)
18. \(\sin \left( \dfrac{\pi}{12} \right)\)
19. \(\cot \left( \dfrac{11\pi}{12} \right)\)
20. \(\csc \left( \dfrac{5\pi}{12} \right)\)
21. \(\sec \left( -\dfrac{\pi}{12} \right)\)
22. Si\(\alpha\) es un ángulo Cuadrante IV con\(\cos(\alpha) = \dfrac{\sqrt{5}}{5}\), y\(\sin(\beta) = \dfrac{\sqrt{10}}{10}\), dónde\(\dfrac{\pi}{2} < \beta < \pi\), encontrar
    1. \(\cos(\alpha + \beta)\)
    2. \(\sin(\alpha + \beta)\)
    3. \(\tan(\alpha + \beta)\)
    4. \(\cos(\alpha - \beta)\)
    5. \(\sin(\alpha - \beta)\)
    6. \(\tan(\alpha - \beta)\)
23. Si\(\csc(\alpha) = 3\), donde\(0 < \alpha < \dfrac{\pi}{2}\), y\(\beta\) es un ángulo del Cuadrante II con\(\tan(\beta) = -7\), encontrar
    1. \(\cos(\alpha + \beta)\)
    2. \(\sin(\alpha + \beta)\)
    3. \(\tan(\alpha + \beta)\)
    4. \(\cos(\alpha - \beta)\)
    5. \(\sin(\alpha - \beta)\)
    6. \(\tan(\alpha - \beta)\)
24. Si\(\sin(\alpha) = \dfrac{3}{5}\)\(0 < \alpha < \dfrac{\pi}{2}\), dónde y\(\cos(\beta) = \dfrac{12}{13}\) dónde\(\dfrac{3\pi}{2} < \beta < 2\pi\), encontrar
    1. \(\sin(\alpha + \beta)\)
    2. \(\cos(\alpha - \beta)\)
    3. \(\tan(\alpha - \beta)\)
25. Si\(\sec(\alpha) = -\dfrac{5}{3}\)\(\dfrac{\pi}{2} < \alpha < \pi\), dónde y dónde\(\tan(\beta) = \dfrac{24}{7}\)\(\pi < \beta < \dfrac{3\pi}{2}\), encontrar
    1. \(\csc(\alpha - \beta)\)
    2. \(\sec(\alpha + \beta)\)
    3. \(\cot(\alpha + \beta)\)

En los Ejercicios 26 - 38, verificar la identidad.

26. \(\cos(\theta - \pi) = -\cos(\theta)\)
27. \(\sin(\pi - \theta) = \sin(\theta)\)
28. \(\tan\left(\theta + \dfrac{\pi}{2} \right) = -\cot(\theta)\)
29. \(\sin(\alpha + \beta) + \sin(\alpha - \beta) = 2\sin(\alpha)\cos(\beta)\)
30. \(\sin(\alpha + \beta) - \sin(\alpha - \beta) = 2\cos(\alpha) \sin(\beta)\)
31. \(\cos(\alpha + \beta) + \cos(\alpha - \beta) = 2\cos(\alpha) \cos(\beta)\)
32. \(\cos(\alpha + \beta) - \cos(\alpha - \beta) = -2\sin(\alpha) \sin(\beta)\)
33. \(\dfrac{\sin(\alpha+\beta)}{\sin(\alpha-\beta)} = \dfrac{1+\cot(\alpha) \tan(\beta)}{1 - \cot(\alpha) \tan(\beta)}\)
34. \(\dfrac{\cos(\alpha + \beta)}{\cos(\alpha - \beta)} = \dfrac{1 - \tan(\alpha)\tan(\beta)}{1 + \tan(\alpha)\tan(\beta)}\)
35. \(\dfrac{\tan(\alpha + \beta)}{\tan(\alpha - \beta)} = \dfrac{\sin(\alpha)\cos(\alpha) + \sin(\beta)\cos(\beta)}{\sin(\alpha)\cos(\alpha) - \sin(\beta)\cos(\beta)}\)
36. \(\dfrac{\sin(t + h) - \sin(t)}{h} = \cos(t) \left(\dfrac{\sin(h)}{h} \right) + \sin(t) \left( \dfrac{\cos(h) - 1}{h} \right)\)
37. \(\dfrac{\cos(t + h) - \cos(t)}{h} = \cos(t) \left( \dfrac{\cos(h) - 1}{h} \right) - \sin(t) \left(\dfrac{\sin(h)}{h} \right)\)
38. \(\dfrac{\tan(t + h) - \tan(t)}{h} = \left( \dfrac{\tan(h)}{h} \right) \left(\dfrac{\sec^{2}(t)}{1 - \tan(t)\tan(h)} \right)\)

En Ejercicios 39 - 48, usa las Fórmulas de Medio Ángulo para encontrar el valor exacto. Es posible que también tengas necesidad del Cociente, Recíproco o Identidades Pares/Impares.

39. \(\cos(75^{\circ})\)(comparar con Ejercicio 7)
40. \(\sin(105^{\circ})\)(comparar con Ejercicio 9)
41. \(\cos(67.5^{\circ})\)
42. \(\sin(157.5^{\circ})\)
43. \(\tan(112.5^{\circ})\)
44. \(\cos\left( \dfrac{7\pi}{12} \right)\)(comparar con Ejercicio 16)
45. \(\sin\left( \dfrac{\pi}{12} \right)\)(comparar con Ejercicio 18)
46. \(\cos \left( \dfrac{\pi}{8} \right)\)
47. \(\sin \left( \dfrac{5\pi}{8} \right)\)
48. \(\tan \left( \dfrac{7\pi}{8} \right)\)

En Ejercicios 49 - 58, utilice la información dada acerca de\(\theta\) para encontrar los valores exactos de

• \(\sin(2\theta)\)
• \(\sin\left(\dfrac{\theta}{2}\right)\)
• \(\cos(2\theta)\)
• \(\cos\left(\dfrac{\theta}{2}\right)\)
• \(\tan(2\theta)\)
• \(\tan\left(\dfrac{\theta}{2}\right)\)

49. \(\sin(\theta) = -\dfrac{7}{25}\)donde\(\dfrac{3\pi}{2} < \theta < 2\pi\)
50. \(\cos(\theta) = \dfrac{28}{53}\)donde\(0 < \theta < \dfrac{\pi}{2}\)
51. \(\tan(\theta) = \dfrac{12}{5}\)donde\(\pi < \theta < \dfrac{3\pi}{2}\)
52. \(\csc(\theta) = 4\)donde\(\dfrac{\pi}{2} < \theta < \pi\)
53. \(\cos(\theta) = \dfrac{3}{5}\)donde\(0 < \theta < \dfrac{\pi}{2}\)
54. \(\sin(\theta) = -\dfrac{4}{5}\)donde\(\pi < \theta < \dfrac{3\pi}{2}\)
55. \(\cos(\theta) = \dfrac{12}{13}\)donde\(\dfrac{3\pi}{2} < \theta < 2\pi\)
56. \(\sin(\theta) = \dfrac{5}{13}\)donde\(\dfrac{\pi}{2} < \theta < \pi\)
57. \(\sec(\theta) = \sqrt{5}\)donde\(\dfrac{3\pi}{2} < \theta < 2\pi\)
58. \(\tan(\theta) = -2\)donde\(\dfrac{\pi}{2} < \theta < \pi\)

En los Ejercicios 59 - 73, verificar la identidad. Supongamos que todas las cantidades están definidas.

59. \((\cos(\theta) + \sin(\theta))^2 = 1 + \sin(2\theta)\)
60. \((\cos(\theta) - \sin(\theta))^2 = 1 - \sin(2\theta)\)
61. \(\tan(2\theta) = \dfrac{1}{1-\tan(\theta)} - \dfrac{1}{1+\tan(\theta)}\)
62. \(\csc(2\theta) = \dfrac{\cot(\theta) + \tan(\theta)}{2}\)
63. \(8 \sin^{4}(\theta) = \cos(4\theta) - 4\cos(2\theta)+3\)
64. \(8 \cos^{4}(\theta) = \cos(4\theta) + 4\cos(2\theta)+3\)
65. [sine3theta]\(\sin(3\theta) = 3\sin(\theta) - 4\sin^{3}(\theta)\)
66. \(\sin(4\theta) = 4\sin(\theta)\cos^{3}(\theta) - 4\sin^{3}(\theta)\cos(\theta)\)
67. \(32\sin^{2}(\theta) \cos^{4}(\theta) = 2 + \cos(2\theta) - 2\cos(4\theta) - \cos(6\theta)\)
68. \(32\sin^{4}(\theta) \cos^{2}(\theta) = 2 - \cos(2\theta) - 2\cos(4\theta) + \cos(6\theta)\)
69. \(\cos(4\theta) = 8\cos^{4}(\theta) - 8\cos^{2}(\theta) + 1\)
70. \(\cos(8\theta) = 128\cos^{8}(\theta)-256\cos^{6}(\theta)+160\cos^{4}(\theta)-32\cos^{2}(\theta)+1\)(SUMINISTRO: Utilice el resultado para 69.)
71. \(\sec(2\theta) = \dfrac{\cos(\theta)}{\cos(\theta) + \sin(\theta)} + \dfrac{\sin(\theta)}{\cos(\theta)-\sin(\theta)}\)
72. \(\dfrac{1}{\cos(\theta) - \sin(\theta)} + \dfrac{1}{\cos(\theta) + \sin(\theta)} = \dfrac{2\cos(\theta)}{\cos(2\theta)}\)
73. \(\dfrac{1}{\cos(\theta) - \sin(\theta)} - \dfrac{1}{\cos(\theta) + \sin(\theta)} = \dfrac{2\sin(\theta)}{\cos(2\theta)}\)

En los Ejercicios 74 - 79, escribe el producto dado como suma. Es posible que necesites usar una Identidad Par/Impar.

74. \(\cos(3\theta)\cos(5\theta)\)
75. \(\sin(2\theta)\sin(7\theta)\)
76. \(\sin(9\theta)\cos(\theta)\)
77. \(\cos(2\theta) \cos(6\theta)\)
78. \(\sin(3\theta) \sin(2\theta)\)
79. \(\cos(\theta) \sin(3\theta)\)

En Ejercicios 80 - 85, escribe la suma dada como producto. Es posible que deba usar una Identidad Par/Impar o Cofunción.

80. \(\cos(3\theta) + \cos(5\theta)\)
81. \(\sin(2\theta) - \sin(7\theta)\)
82. \(\cos(5\theta) - \cos(6\theta)\)
83. \(\sin(9\theta) - \sin(-\theta)\)
84. \(\sin(\theta) + \cos(\theta)\)
85. \(\cos(\theta) - \sin(\theta)\)
86. Supongamos que\(\theta\) es un cuadrante con el ángulo\(\sin(\theta) = x\) I. Verificar las siguientes fórmulas
    1. \(\cos(\theta) = \sqrt{1-x^2}\)
    2. \(\sin(2\theta) = 2x\sqrt{1-x^2}\)
    3. \(\cos(2\theta) = 1 - 2x^2\)
87. Discuta con tus compañeros de clase cómo cambia cada una de las fórmulas, si las hay, en el Ejercicio 86 si cambiamos suponemos que\(\theta\) es un ángulo Cuadrante II, III o IV.
88. Supongamos que\(\theta\) es un cuadrante con el ángulo\(\tan(\theta) = x\) I. Verificar las siguientes fórmulas
    1. \(\cos(\theta) = \dfrac{1}{\sqrt{x^2+1}}\)
    2. \(\sin(\theta) = \dfrac{x}{\sqrt{x^2+1}}\)
    3. \(\sin(2\theta) = \dfrac{2x}{x^2+1}\)
    4. \(\cos(2\theta) = \dfrac{1-x^2}{x^2+1}\)
89. Discuta con tus compañeros de clase cómo cambia cada una de las fórmulas, si las hay, en el Ejercicio 88 si cambiamos suponemos que\(\theta\) es un ángulo Cuadrante II, III o IV.
90. Si es\(\sin(\theta) = \dfrac{x}{2}\) por\(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), encuentra una expresión para\(\cos(2\theta)\) en términos de\(x\).
91. Si es\(\tan(\theta) = \dfrac{x}{7}\) por\(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), encuentra una expresión para\(\sin(2\theta)\) en términos de\(x\).
92. Si es\(\sec(\theta) = \dfrac{x}{4}\) por\(0 < \theta < \dfrac{\pi}{2}\), encuentra una expresión para\(\ln|\sec(\theta) + \tan(\theta)|\) en términos de\(x\).
93. \(\cos^{2}(\theta) - \sin^{2}(\theta) = 2\cos^{2}(\theta) - 1 = 1 - 2\sin^{2}(\theta)\)Demuéstralo para todos\(\theta\).
94. Dejar\(\theta\) ser un ángulo Cuadrante III con\(\cos(\theta) = -\dfrac{1}{5}\). Demostrar que esta no es suficiente información para determinar el signo de\(\sin\left(\dfrac{\theta}{2}\right)\) asumiendo primero\(3\pi < \theta < \dfrac{7\pi}{2}\) y luego asumiendo\(\pi < \theta < \dfrac{3\pi}{2}\) y calculando\(\sin\left(\dfrac{\theta}{2}\right)\) en ambos casos.
95. Sin usar tu calculadora, demuéstralo\(\dfrac{\sqrt{2 + \sqrt{3}}}{2} = \dfrac{\sqrt{6} + \sqrt{2}}{4}\)
96. En la parte 4 del Ejemplo 10.4.3, escribimos\(\cos(3\theta)\) como polinomio en términos de\(\cos(\theta)\). En el Ejercicio 69, te hicimos verificar una identidad que\(\cos(4\theta)\) se expresa como polinomio en términos de\(\cos(\theta)\). ¿Se puede encontrar un polinomio en términos de\(\cos(\theta)\) for\(\cos(5\theta)\)? \(\cos(6\theta)\)? ¿Se puede encontrar un patrón para que\(\cos(n\theta)\) pueda escribirse como polinomio en coseno para cualquier número natural\(n\)?
97. En el Ejercicio 65, te hacemos verificar una identidad que\(\sin(3\theta)\) se expresa como polinomio en términos de\(\sin(\theta)\). ¿Puedes hacer lo mismo por\(\sin(5\theta)\)? ¿Y para qué\(\sin(4\theta)\)? Si no, ¿qué sale mal?
98. Verificar las Identidades Pares/Impares para tangente, secante, cosecante y cotangente.
99. Verificar las identidades de cofunción para tangente, secante, cosecante y cotangente.
100. Verificar las identidades de diferencia para seno y tangente.
101. Verificar el producto para sumar identidades.
102. Verificar la suma a las identidades del producto.

10.4.2. RESPUESTAS

7. \(\cos(75^{\circ}) = \dfrac{\sqrt{6} - \sqrt{2}}{4}\)
8. \(\sec(165^{\circ}) = -\dfrac{4}{\sqrt{2}+\sqrt{6}} = \sqrt{2} - \sqrt{6}\)
9. \(\sin(105^{\circ}) = \dfrac{\sqrt{6}+\sqrt{2}}{4}\)
10. \(\csc(195^{\circ}) = \dfrac{4}{\sqrt{2}-\sqrt{6}} = -(\sqrt{2}+\sqrt{6})\)
11. \(\cot(255^{\circ}) = \dfrac{\sqrt{3}-1}{\sqrt{3}+1} = 2-\sqrt{3}\)
12. \(\tan(375^{\circ}) = \dfrac{3-\sqrt{3}}{3+\sqrt{3}} = 2-\sqrt{3}\)
13. \(\cos\left(\dfrac{13\pi}{12}\right) = -\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
14. \(\sin\left(\dfrac{11\pi}{12}\right) = \dfrac{\sqrt{6} - \sqrt{2}}{4}\)
15. \(\tan\left(\dfrac{13\pi}{12}\right) = \dfrac{3-\sqrt{3}}{3+\sqrt{3}} = 2-\sqrt{3}\)
16. \(\cos \left( \dfrac{7\pi}{12} \right) = \dfrac{\sqrt{2} - \sqrt{6}}{4}\)
17. \(\tan \left( \dfrac{17\pi}{12} \right) = 2 + \sqrt{3}\)
18. \(\sin \left( \dfrac{\pi}{12} \right) = \dfrac{\sqrt{6} - \sqrt{2}}{4}\)
19. \(\cot \left( \dfrac{11\pi}{12} \right) = -(2 + \sqrt{3})\)
20. \(\csc \left( \dfrac{5\pi}{12} \right) = \sqrt{6} - \sqrt{2}\)
21. \(\sec \left( -\dfrac{\pi}{12} \right) = \sqrt{6} - \sqrt{2}\)
22. 1. \(\cos(\alpha + \beta) = -\dfrac{\sqrt{2}}{10}\)
    2. \(\sin(\alpha + \beta) = \dfrac{7\sqrt{2}}{10}\)
    3. \(\sin(\alpha - \beta) = \dfrac{\sqrt{2}}{2}\)
    4. \(\tan(\alpha - \beta) = -1\)
    5. \(\tan(\alpha + \beta) = -7\)
    6. \(\cos(\alpha - \beta)= -\dfrac{\sqrt{2}}{2}\)
23. 1. \(\cos(\alpha + \beta) = - \dfrac{4+7\sqrt{2}}{30}\)
    2. \(\sin(\alpha + \beta) = \dfrac{28-\sqrt{2}}{30}\)
    3. \(\sin(\alpha - \beta) = - \dfrac{28+\sqrt{2}}{30}\)
    4. \(\tan(\alpha - \beta)= \dfrac{28+\sqrt{2}}{4-7\sqrt{2}} = -\dfrac{63+100\sqrt{2}}{41}\)
    5. \(\tan(\alpha + \beta) = \dfrac{-28+\sqrt{2}}{4+7\sqrt{2}} = \dfrac{63-100\sqrt{2}}{41}\)
    6. \(\cos(\alpha - \beta) = \dfrac{-4+7\sqrt{2}}{30}\)
24. 1. \(\sin(\alpha + \beta) = \dfrac{16}{65}\)
    2. \(\cos(\alpha - \beta) = \dfrac{33}{65}\)
    3. \(\tan(\alpha - \beta) = \dfrac{56}{33}\)
25. 1. \(\csc(\alpha - \beta) = -\dfrac{5}{4}\)
    2. \(\sec(\alpha + \beta) = \dfrac{125}{117}\)
    3. \(\cot(\alpha + \beta) = \dfrac{117}{44}\)

39. \(\cos(75^{\circ}) = \dfrac{\sqrt{2-\sqrt{3}}}{2}\)
40. \(\sin(105^{\circ}) = \dfrac{\sqrt{2+\sqrt{3}}}{2}\)
41. \(\cos(67.5^{\circ}) = \dfrac{\sqrt{2-\sqrt{2}}}{2}\)
42. \(\sin(157.5^{\circ}) = \dfrac{\sqrt{2-\sqrt{2}}}{2}\)
43. \(\tan(112.5^{\circ}) = - \sqrt{\dfrac{2+\sqrt{2}}{2-\sqrt{2}}} = -1 - \sqrt{2}\)
44. \(\cos\left( \dfrac{7\pi}{12} \right) = -\dfrac{\sqrt{2-\sqrt{3}}}{2}\)
45. \(\sin\left( \dfrac{\pi}{12} \right) = \dfrac{\sqrt{2-\sqrt{3}}}{2}\)
46. \(\cos \left( \dfrac{\pi}{8} \right) = \dfrac{\sqrt{2 + \sqrt{2}}}{2}\)
47. \(\sin \left( \dfrac{5\pi}{8} \right) = \dfrac{\sqrt{2 + \sqrt{2}}}{2}\)
48. \(\tan \left( \dfrac{7\pi}{8} \right) = -\sqrt{ \dfrac{2 - \sqrt{2}}{2 + \sqrt{2}} } =1-\sqrt{2}\)
49. • \(\sin(2\theta) = -\dfrac{336}{625}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{2}}{10}\)
    • \(\cos(2\theta) = \dfrac{527}{625}\)
    • \(\cos\left(\frac{\theta}{2}\right) = -\dfrac{7\sqrt{2}}{10}\)
    • \(\tan(2\theta) = -\dfrac{336}{527}\)
    • \(\tan\left(\frac{\theta}{2}\right) = -\dfrac{1}{7}\)
50. • \(\sin(2\theta) = \dfrac{2520}{2809}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{5\sqrt{106}}{106}\)
    • \(\cos(2\theta) = -\dfrac{1241}{2809}\)
    • \(\cos\left(\frac{\theta}{2}\right) = \dfrac{9\sqrt{106}}{106}\)
    • \(\tan(2\theta) = -\dfrac{2520}{1241}\)
    • \(\tan\left(\frac{\theta}{2}\right) = \dfrac{5}{9}\)
51. • \(\sin(2\theta) = \dfrac{120}{169}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{3\sqrt{13}}{13}\)
    • \(\cos(2\theta) = -\dfrac{119}{169}\)
    • \(\cos\left(\frac{\theta}{2}\right) = -\dfrac{2\sqrt{13}}{13}\)
    • \(\tan(2\theta) = -\dfrac{120}{119}\)
    • \(\tan\left(\frac{\theta}{2}\right) = -\dfrac{3}{2}\)
52. • \(\sin(2\theta) = -\dfrac{\sqrt{15}}{8}\)
    • \(\sin\left(\frac{\theta}{2}\right) =\dfrac{\sqrt{8+2\sqrt{15}}}{4} \\ \phantom{\tan\left(\frac{\theta}{2}\right) = 4+\sqrt{15}}\)
    • \(\cos(2\theta) = \dfrac{7}{8}\)
    • \(\cos\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{8-2\sqrt{15}}}{4} \\ \phantom{\tan\left(\frac{\theta}{2}\right) = 4+\sqrt{15}}\)
    • \(\tan(2\theta) = -\dfrac{\sqrt{15}}{7}\)
    • \(\tan\left(\frac{\theta}{2}\right) = \sqrt{\dfrac{8+2\sqrt{15}}{8-2\sqrt{15}}} \\ \tan\left(\frac{\theta}{2}\right) = 4+\sqrt{15}\)
53. • \(\sin(2\theta) = \dfrac{24}{25}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{5}}{5}\)
    • \(\cos(2\theta) = -\dfrac{7}{25}\)
    • \(\cos\left(\frac{\theta}{2}\right) = \dfrac{2\sqrt{5}}{5}\)
    • \(\tan(2\theta)=-\dfrac{24}{7}\)
    • \(\tan\left(\frac{\theta}{2}\right) = \dfrac{1}{2}\)
54. • \(\sin(2\theta) = \dfrac{24}{25}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{2\sqrt{5}}{5}\)
    • \(\cos(2\theta) = -\dfrac{7}{25}\)
    • \(\cos\left(\frac{\theta}{2}\right) = -\dfrac{\sqrt{5}}{5}\)
    • \(\tan(2\theta)=-\dfrac{24}{7}\)
    • \(\tan\left(\frac{\theta}{2}\right) = -2\)
55. • \(\sin(2\theta) = -\dfrac{120}{169}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{26}}{26}\)
    • \(\cos(2\theta) = \dfrac{119}{169}\)
    • \(\cos\left(\frac{\theta}{2}\right) = -\dfrac{5\sqrt{26}}{26}\)
    • \(\tan(2\theta)=-\dfrac{120}{119}\)
    • \(\tan\left(\frac{\theta}{2}\right) = -\dfrac{1}{5}\)
56. • \(\sin(2\theta) = -\dfrac{120}{169}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{5\sqrt{26}}{26}\)
    • \(\cos(2\theta) = \dfrac{119}{169}\)
    • \(\cos\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{26}}{26}\)
    • \(\tan(2\theta)=-\dfrac{120}{119}\)
    • \(\tan\left(\frac{\theta}{2}\right) = 5\)
57. • \(\sin(2\theta) = -\dfrac{4}{5}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{50-10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}\)
    • \(\cos(2\theta) = -\dfrac{3}{5}\)
    • \(\cos\left(\frac{\theta}{2}\right)= -\dfrac{\sqrt{50+10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}\)
    • \(\tan(2\theta)=\dfrac{4}{3}\)
    • \(\tan\left(\frac{\theta}{2}\right) = -\sqrt{\dfrac{5-\sqrt{5}}{5+\sqrt{5}}} \\ \tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}\)
58. • \(\sin(2\theta) = -\dfrac{4}{5}\)
    • \(\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{50+10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}\)
    • \(\cos(2\theta) = -\dfrac{3}{5}\)
    • \(\cos\left(\frac{\theta}{2}\right)= \dfrac{\sqrt{50-10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}\)
    • \(\tan(2\theta)=\dfrac{4}{3}\)
    • \(\tan\left(\frac{\theta}{2}\right) = \sqrt{\dfrac{5+\sqrt{5}}{5-\sqrt{5}}} \\ \tan\left(\frac{\theta}{2}\right) =\dfrac{5+5\sqrt{5}}{10}\)

74. \(\dfrac{\cos(2\theta) + \cos(8\theta)}{2}\)
75. \(\dfrac{\cos(5\theta) - \cos(9\theta)}{2}\)
76. \(\dfrac{\sin(8\theta) + \sin(10\theta)}{2}\)
77. \(\dfrac{\cos(4\theta) + \cos(8\theta)}{2}\)
78. \(\dfrac{\cos(\theta) - \cos(5\theta)}{2}\)
79. \(\dfrac{\sin(2\theta) + \sin(4\theta)}{2}\)
80. \(2\cos(4\theta)\cos(\theta)\)
81. \(-2\cos \left( \dfrac{9}{2}\theta \right) \sin \left( \dfrac{5}{2}\theta \right)\)
82. \(2\sin \left( \dfrac{11}{2}\theta \right) \sin \left( \dfrac{1}{2}\theta \right)\)
83. \(2\cos(4\theta)\sin(5\theta)\)
84. \(\sqrt{2}\cos \left(\theta - \dfrac{\pi}{4} \right)\)
85. \(-\sqrt{2}\sin \left(\theta - \dfrac{\pi}{4} \right)\)

90. \(1 - \dfrac{x^{2}}{2}\)
91. \(\dfrac{14x}{x^{2} + 49}\)
92. \(\ln |x + \sqrt{x^{2} + 16}| - \ln(4)\)

---

Referencia

¹ Como se mencionó al final de la Sección 10.2, las propiedades de las funciones circulares cuando se consideran funciones de ángulos en la medida de radianes se mantienen igualmente bien si vemos estas funciones como funciones de números reales. No es sorprendente que las propiedades Even/Odd de las funciones circulares se llamen así porque identifican coseno y secante como funciones pares, mientras que las cuatro funciones circulares restantes son impares. (Ver Sección 1.6.)

² En el cuadro que hemos dibujado, los triángulos\(POQ\) y\(AOB\) son congruentes, lo que es aún mejor. No obstante,\(\alpha_{0}-\beta_{0}\) podría ser 0 o podría ser\(\pi\), ninguno de los cuales hace un triángulo. También podría ser más grande que\(\pi\), lo que hace un triángulo, simplemente no el que hemos dibujado. Deberías pensar en esos tres casos.

³ Estas también son conocidas como las Fórmulas de Próstaféresis y tienen una rica historia. Los autores recomiendan que realice algunas investigaciones sobre ellos según lo permita su horario.