10.5: Gráficas de las Funciones Trigonométricas

En esta sección, volvemos a nuestra discusión de las funciones circulares (trigonométricas) como funciones de números reales y retomamos donde lo dejamos en las Secciones 10.2.1 y 10.3.1. Como es habitual, comenzamos nuestro estudio con las funciones\(f(t) = \cos(t)\) y\(g(t) = \sin(t)\).

10.5.1 Gráficas de las funciones coseno y seno

Del Teorema 10.5 en la Sección 10.2.1, sabemos que el dominio de\(f(t) = \cos(t)\) y de\(g(t) = \sin(t)\) es todo números reales,\((-\infty, \infty),\) y el rango de ambas funciones es\([-1,1]\). Las Identidades Pares/Impares en el Teorema 10.12 nos dicen\(\cos(-t) = \cos(t)\) para todos los números reales\(t\) y\(\sin(-t) = -\sin(t)\) para todos los números reales\(t\). Esto significa que\(f(t) = \cos(t)\) es una función par, mientras que\(g(t) = \sin(t)\) es una función impar. ¹ Otra propiedad importante de estas funciones es la de los ángulos coterminales\(\alpha\) y\(\beta\),\(\cos(\alpha) = \cos(\beta)\) y\(\sin(\alpha) = \sin(\beta)\). Dicho de otra manera,\(\cos(t + 2\pi k) = \cos(t)\) y\(\sin(t + 2\pi k) = \sin(t)\) para todos los números reales\(t\) y cualquier entero\(k\). A esta última propiedad se le da un nombre especial.

Definición 10.3. Funciones Periódicas

Se dice que una función\(f\) es periódica si hay un número real\(f(t+c) = f(t)\) para\(c\) que para todos los números reales\(t\) en el dominio de\(f\). El número positivo más pequeño\(p\) para el cual\(f(t+p) = f(t)\) para todos los números reales\(t\) en el dominio de\(f\), si existe, se llama el periodo de\(f\).

Ya hemos visto una familia de funciones periódicas en la Sección 2.1: las funciones constantes. Sin embargo, a pesar de ser periódica una función constante no tiene periodo. (Dejaremos esa extraña gema como ejercicio para ti.) Volviendo a las funciones circulares, vemos que por Definición 10.3,\(f(t) = \cos(t)\) es periódica, ya que\(\cos(t + 2\pi k) = \cos(t)\) para cualquier entero\(k\). Para determinar el periodo de\(f\), necesitamos encontrar el número real más pequeño\(f(t+p) = f(t)\) para\(p\) que para todos los números reales\(t\) o, dicho de otra manera, el número real positivo más pequeño\(p\) tal que\(\cos(t+p) = \cos(t)\) para todos los números reales\(t\). Sabemos que\(\cos(t + 2\pi) = \cos(t)\) para todos los números reales\(t\) pero la pregunta sigue siendo si algún número real menor va a hacer el truco. Supongamos\(p>0\) y\(\cos(t + p) = \cos(t)\) para todos los números reales\(t\). Entonces, en particular,\(\cos(0+p) = \cos(0)\) para que\(\cos(p) = 1\). De esto sabemos que\(p\) es un múltiplo de\(2\pi\) y, dado que el múltiplo positivo más pequeño de\(2\pi\) es\(2\pi\) en sí mismo, tenemos el resultado. De igual manera, podemos mostrar\(g(t) = \sin(t)\) que también es periódico con\(2\pi\) como su periodo. ² Tener periodo\(2\pi\) esencialmente significa que podemos entender completamente todo sobre las funciones\(f(t) = \cos(t)\) y\(g(t) = \sin(t)\) estudiando un intervalo de longitud\(2\pi\), digamos\([0,2\pi]\). ³

Una última propiedad de las funciones\(f(t) = \cos(t)\) y\(g(t) = \sin(t)\) vale la pena señalar: ambas funciones son continuas y fluidas. Recordemos de la Sección 3.1 que geométricamente esto significa que las gráficas de las funciones coseno y seno no tienen saltos, huecos, agujeros en la gráfica, asíntotas, esquinas o cúspides. Como veremos, las gráficas de ambos\(f(t) = \cos(t)\) y\(g(t) = \sin(t)\) serpentea amablemente y no causan ningún problema. Resumimos estos hechos en el siguiente teorema.

Teorema 10.22. Propiedades de las funciones coseno y seno

La función\(f(x) = \cos(x)\) tiene dominio\((-\infty, \infty)\) tiene rango\([-1,1]\) es continuo y suave es parejo tiene periodo\(2\pi\)

La función\(g(x) = \sin(x)\) tiene dominio\((-\infty, \infty)\) tiene rango\([-1,1]\) es continuo y suave es impar tiene periodo\(2\pi\)

En la tabla anterior, seguimos la convención establecida en la Sección 1.6 y utilizada\(x\) como variable independiente y\(y\) como variable dependiente. ⁵ Esto nos permite dirigir nuestra atención a graficar las funciones coseno y seno en el Plano Cartesiano. Para graficar\(y = \cos(x)\), hacemos una tabla como hicimos en la Sección 1.6 usando algunos de los 'valores comunes' de\(x\) en el intervalo\([0,2\pi]\). Esto genera una porción de la gráfica coseno, que llamamos el 'ciclo fundamental' de\(y = \cos(x)\).

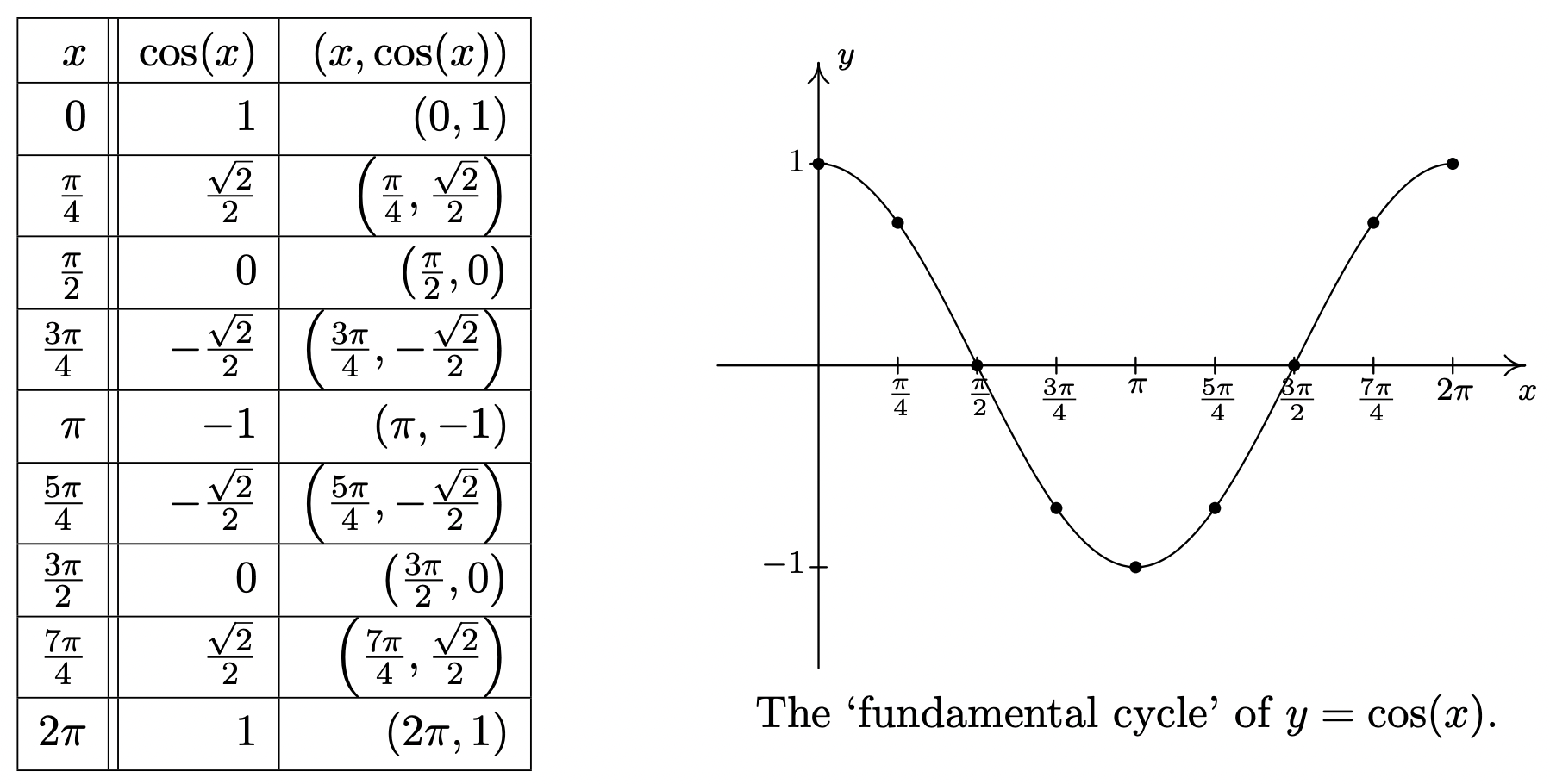
Algunas cosas sobre la gráfica anterior son dignas de mención. En primer lugar, esta gráfica representa sólo una parte de la gráfica de\(y = \cos(x)\). Para obtener toda la gráfica, imaginamos 'copiar y pegar' esta gráfica de extremo a extremo infinitamente en ambas direcciones (izquierda y derecha) en el\(x\) eje -eje. En segundo lugar, la escala vertical aquí ha sido muy exagerada para mayor claridad y estética. A continuación se muestra un gráfico exacto a escala\(y = \cos(x)\) que muestra varios ciclos con el 'ciclo fundamental' trazado más grueso que los otros. El gráfico de generalmente\(y=\cos(x)\) se describe como “tipo onda”; de hecho, muchas de las aplicaciones que involucran las funciones coseno y seno presentan fenómenos similares a ondas de modelado.

Un gráfico a escala precisa de\(y=\cos (x)\).

Podemos trazar el ciclo fundamental de la gráfica de\(y = \sin(x)\) manera similar, con resultados similares.

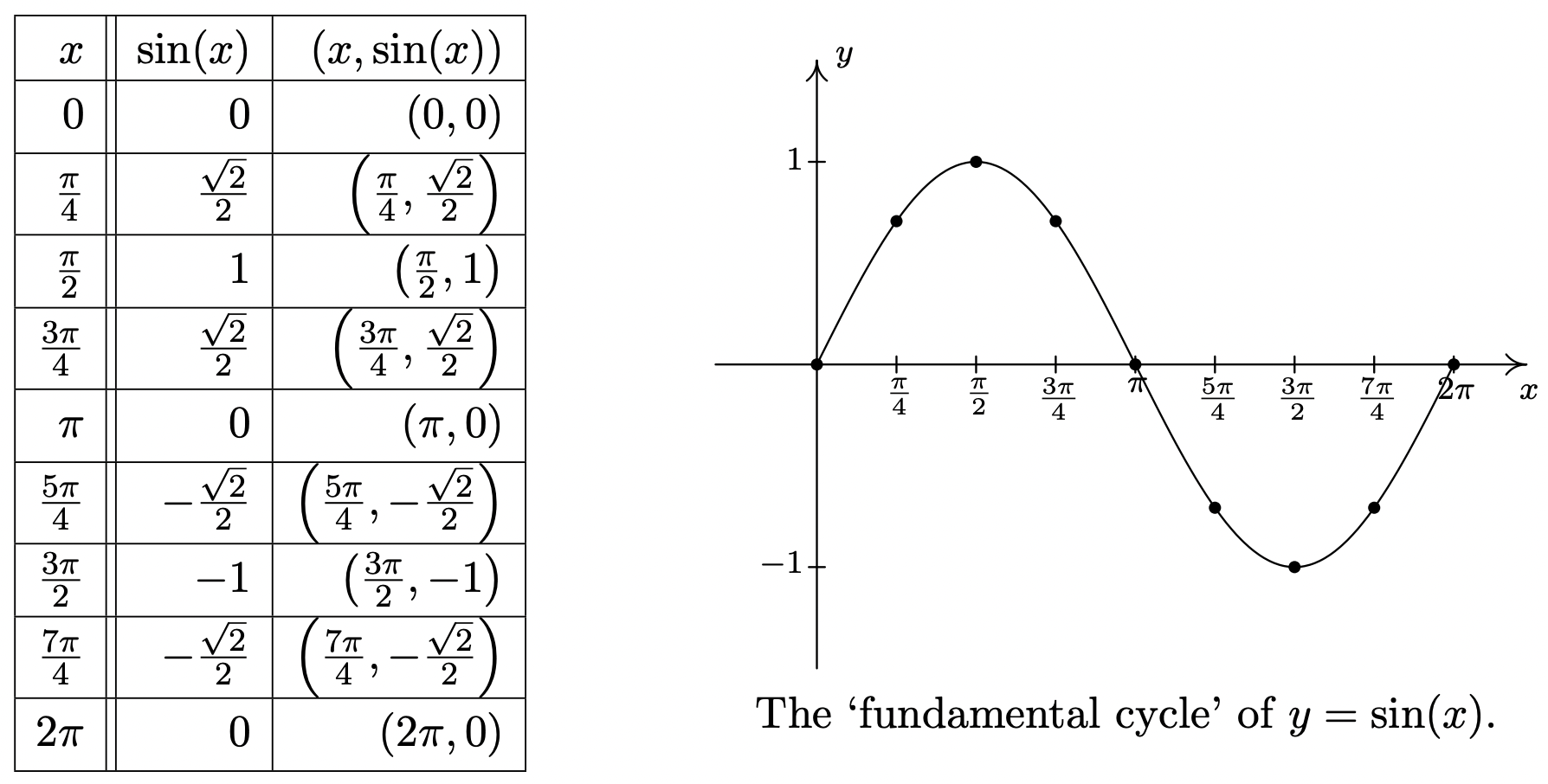
Al igual que con la gráfica de\(y=\cos(x)\), proporcionamos una gráfica a escala precisa de\(y = \sin(x)\) abajo con el ciclo fundamental resaltado.

Un gráfico escalado con precisión\(y=\sin (x)\).

No es casualidad que las gráficas de\(y = \cos(x)\) y\(y = \sin(x)\) sean tan similares. Usando una identidad de cofunción junto con la propiedad par del coseno, tenemos

\[\sin(x) = \cos\left(\frac{\pi}{2} - x\right) = \cos\left(-\left(x - \frac{\pi}{2}\right)\right) = \cos\left(x - \frac{\pi}{2}\right)\nonumber\]

Recordando la Sección 1.7, vemos a partir de esta fórmula que la gráfica de\(y=\sin(x)\) es el resultado de desplazar la gráfica de\(y = \cos(x)\) a las\(\frac{\pi}{2}\) unidades correctas. Una inspección visual lo confirma.

Ahora que conocemos las formas básicas de las gráficas de\(y = \cos(x)\) y\(y = \sin(x)\), podemos usar el Teorema 1.7 en la Sección 1.7 para graficar curvas más complicadas. Para ello, necesitamos hacer un seguimiento del movimiento de algunos puntos clave en las gráficas originales. Elegimos rastrear los valores\(x = 0\),\(\frac{\pi}{2}\),\(\pi\),\(\frac{3\pi}{2}\) y\(2\pi\). Estas 'marcas cuartoras' corresponden a ángulos cuadrangulares, y como tales, marcan la ubicación de los ceros y los extremos locales de estas funciones durante exactamente un periodo. Antes de comenzar nuestro siguiente ejemplo, necesitamos revisar el concepto del 'argumento' de una función como se introdujo por primera vez en la Sección 1.4. Para la función\(f(x) = 1 - 5\cos(2x-\pi)\), el argumento de\(f\) es\(x\). Tendremos ocasión, sin embargo, de referirnos al argumento del coseno, que en este caso lo es\(2x-\pi\). Dicho de manera poco clara, el argumento de una función trigonométrica es la expresión 'dentro' de la función.

Ejemplo 10.5.1.

Grafique un ciclo de las siguientes funciones. Declarar el periodo de cada uno.

1. \(f(x) = 3 \cos\left(\frac{\pi x - \pi}{2}\right) + 1\)
2. \(g(x) = \frac{1}{2} \sin(\pi - 2x) + \frac{3}{2}\)

Solución.

1. Ponemos el argumento del coseno,\(\frac{\pi x - \pi}{2}\), igual a cada uno de los valores:\(0\),,\(\frac{\pi}{2}\),\(\pi\)\(\frac{3\pi}{2}\),\(2\pi\) y resolvemos para\(x\). Resumimos los resultados a continuación. \ [\ begin {array} {|r|c|c|}
   \ hline a &\ frac {\ pi x-\ pi} {2} =a & x\
   \ hline 0 &\ frac {\ pi x-\ pi} {2} =0 & 1\
   \ hline\ frac {\ pi} {2} &\ frac {\ pi x-\ pi} {2} =\ frac {\ pi} {2} & 2\
   \ hline\ pi &\ frac {\ pi x-\ pi} {2} =\ pi & amp; 3\
   \ hline\ frac {3\ pi} {2} &\ frac {\ pi x-\ pi} {2} =\ frac {3\ pi} {2} & 4\
   \ hline 2\ pi &\ frac {\ pi x-\ pi} {2} =2\ pi & 5\
   \ hline
   \ end {array}\ nonumber\]

   A continuación, sustituimos cada uno de estos\(x\) valores en\(f(x) = 3 \cos\left(\frac{\pi x - \pi}{2}\right) + 1\) para determinar los\(y\) valores correspondientes y conectar los puntos de una manera agradable en forma de onda.

   

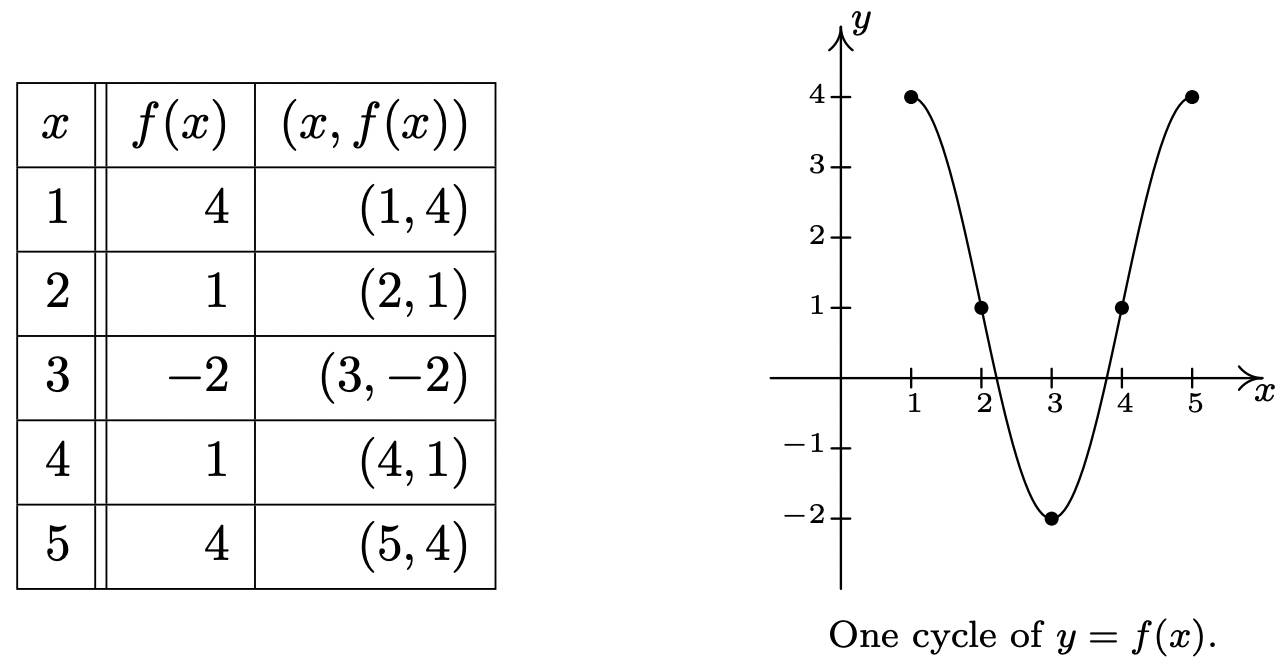
   Se grafica un ciclo de\([1,5]\) manera que el periodo es la longitud de ese intervalo que es\(4\).

2. Procediendo como antes, establecemos el argumento del seno,\(\pi - 2x\), igual a cada una de nuestras marcas de cuarto y resolvemos para\(x\).

   \ [\ begin {array} {|r|r|r|}
   \ hline a &\ pi-2 x=a & x\
   \ hline 0 &\ pi-2 x=0 &\ frac {\ pi} {2}\
   \ hline\ frac {\ pi} {2} &\ pi-2 x=\ frac {\ pi} {2} &\ frac {\ pi} {4}\\
   \ hline\ pi &\ pi-2 x=\ pi & 0\\
   \ hline\ frac {3\ pi} {2} &\ pi-2 x=\ frac {3\ pi} {2} & -\ frac {\ pi} {4}\
   \\ hline 2\ pi &\ pi-2 x=2\ pi & -\ frac {\ pi} {2}\
   \ hline
   \ end {array}\ nonumber\]

   Ahora encontramos los\(y\) valores -correspondientes en la gráfica sustituyendo cada uno de estos\(x\) -valores en\(g(x) = \frac{1}{2} \sin(\pi - 2x) + \frac{3}{2}\). Una vez más, conectamos los puntos de una manera ondulada.

   

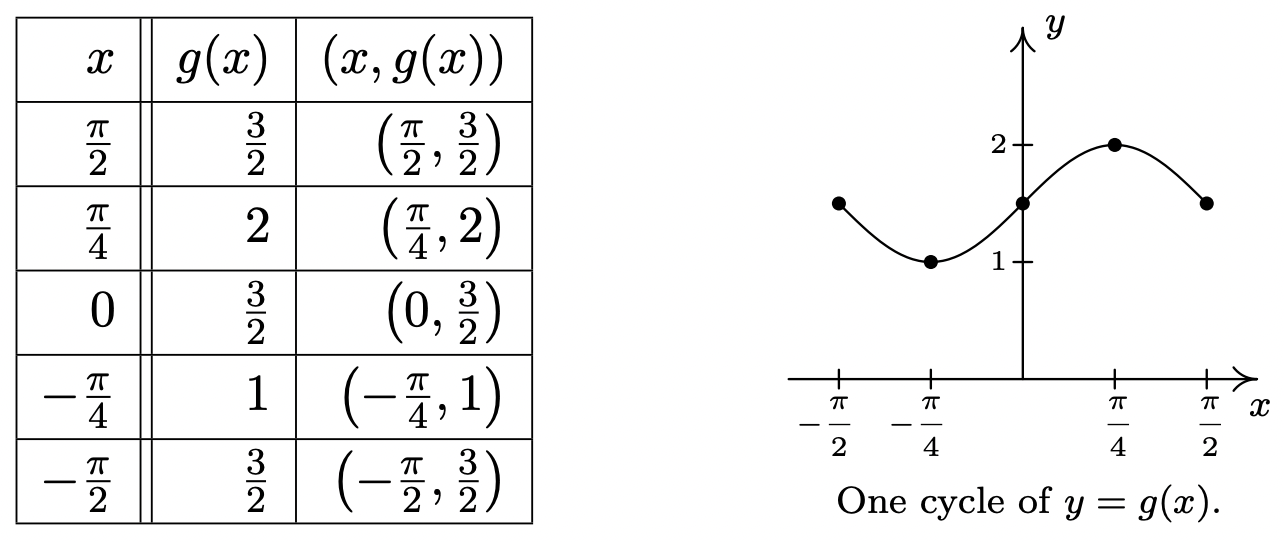
   Se graficó un ciclo en el intervalo\(\left[ -\frac{\pi}{2}, \frac{\pi}{2}\right]\) por lo que el periodo es\(\frac{\pi}{2} - \left(-\frac{\pi}{2}\right) = \pi\).

Las funciones del Ejemplo 10.5.1 son ejemplos de sinusoides. En términos generales, una sinusoide es el resultado de tomar la gráfica básica de\(f(x) = \cos(x)\) o\(g(x) = \sin(x)\) y realizar alguna de las transformaciones ⁶ mencionadas en la Sección 1.7. Los sinusoides pueden caracterizarse por cuatro propiedades: periodo, amplitud, desplazamiento de fase y desplazamiento vertical. Ya hemos discutido periodo, es decir, cuánto tiempo tarda la sinusoide en completar un ciclo. El periodo estándar de ambos\(f(x) = \cos(x)\) y\(g(x) = \sin(x)\) es\(2\pi\), pero las escalaciones horizontales cambiarán el periodo de la sinusoide resultante. La amplitud de la sinusoide es una medida de cuán 'alta' es la onda, como se indica en la siguiente figura. La amplitud de las funciones coseno y seno estándar es\(1\), pero las escalaciones verticales pueden alterarlo.

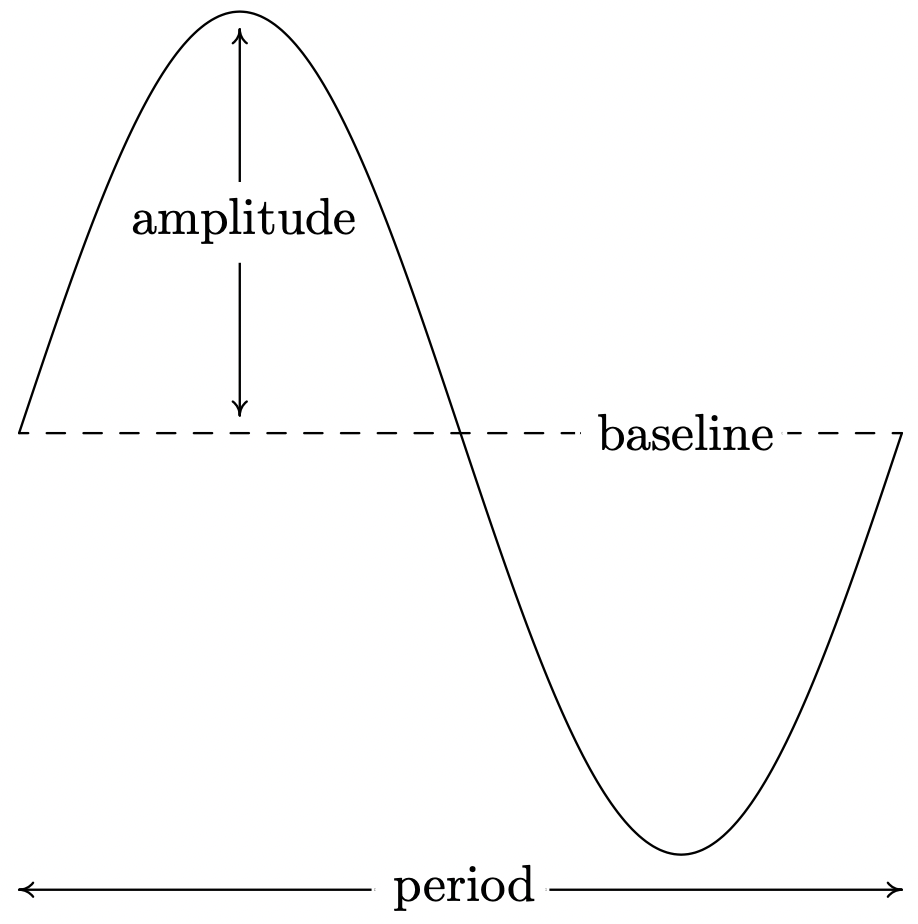
El desplazamiento de fase de la sinusoide es el desplazamiento horizontal experimentado por el ciclo fundamental. Hemos visto que un desplazamiento de fase (horizontal) de\(\frac{\pi}{2}\) hacia la derecha lleva\(f(x) = \cos(x)\) a\(g(x) = \sin(x)\) desde entonces\(\cos\left(x - \frac{\pi}{2}\right) = \sin(x)\). Como el lector puede verificar, un desplazamiento de fase de\(\frac{\pi}{2}\) a la izquierda lleva\(g(x) = \sin(x)\) a\(f(x)= \cos(x)\). El desplazamiento vertical de una sinusoide es exactamente el mismo que los desplazamientos verticales en la Sección 1.7. En la mayoría de los contextos, se supone que el desplazamiento vertical de una sinusoide es\(0\), pero a continuación señalamos el caso más general. El siguiente teorema, que recuerda al Teorema 1.7 en la Sección 1.7, muestra cómo encontrar estas cuatro cantidades fundamentales a partir de la fórmula de la sinusoide dada.

Teorema 10.23.

Para\(\omega > 0\), las funciones\[C(x) = A \cos(\omega x + \phi) + B \quad \text{and} \quad S(x) = A \sin(\omega x + \phi) + B\nonumber\]

• tener periodo\(\dfrac{2\pi}{\omega}\)
• tener amplitud\(|A|\)
• tienen desplazamiento de fase\(-\dfrac{\phi}{\omega}\)
• tener desplazamiento vertical\(B\)

Observamos que en algunos círculos científicos y de ingeniería, la cantidad\(\phi\) mencionada en el Teorema 10.23 se llama la fase de la sinusoide. Dado que nuestro interés en este libro es principalmente con graficar sinusoides, enfocamos nuestra atención en el cambio horizontal\(-\frac{\phi}{\omega}\) inducido por\(\phi\).

La prueba del Teorema 10.23 es una aplicación directa del Teorema 1.7 en la Sección 1.7 y se deja al lector. El parámetro\(\omega\), que se estipula que es positivo, se denomina frecuencia (angular) de la sinusoide y es el número de ciclos que la sinusoide completa a lo largo de un\(2\pi\) intervalo. Siempre podemos asegurar el\(\omega > 0\) uso de las Identidades Pares/Impar. ⁷ Ahora probamos el Teorema 10.23 usando las funciones\(f\) y\(g\) aparece en el Ejemplo 10.5.1. Primero, escribimos\(f(x)\) en la forma prescrita en el Teorema 10.23,

\[f(x) = 3 \cos\left(\frac{\pi x - \pi}{2}\right) + 1 = 3\cos\left(\frac{\pi}{2} x + \left(-\frac{\pi}{2}\right)\right) + 1,\nonumber\]

para que\(A = 3\),\(\omega = \frac{\pi}{2}\),\(\phi = -\frac{\pi}{2}\) y\(B = 1\). Según el Teorema 10.23, el periodo de\(f\) es\(\frac{2\pi}{\omega} = \frac{2\pi}{\pi/2} = 4\), la amplitud es\(|A| = |3| = 3\), el desplazamiento de fase es\(-\frac{\phi}{\omega} = -\frac{-\pi/2}{\pi/2} = 1\) (indicando un desplazamiento a la\(1\) unidad derecha) y el desplazamiento vertical es\(B = 1\) (indicando una\(1\) unidad de desplazamiento hacia arriba). Todos estos coinciden con nuestra gráfica de\(y=f(x)\). Además, si comenzamos con la forma básica de la gráfica coseno, la desplazamos\(1\) unidad hacia la derecha,\(1\) unidad hacia arriba, estiramos la amplitud a\(3\) y encogemos el periodo a\(4\), habremos reconstruido un periodo de la gráfica de\(y=f(x)\). Es decir, en lugar de rastrear las cinco 'marcas de cuarto' a través de las transformaciones para trazar\(y=f(x)\), podemos usar otras cinco piezas de información: el desplazamiento de fase, desplazamiento vertical, amplitud, período y forma básica de la curva coseno. Volviendo nuestra atención ahora a la función\(g\) en el Ejemplo 10.5.1, primero necesitamos usar la propiedad impar de la función sinusoidal para escribirla en la forma requerida por el Teorema 10.23

\[g(x) = \frac{1}{2} \sin(\pi - 2x) + \frac{3}{2} = \frac{1}{2} \sin(-(2x - \pi)) + \frac{3}{2} = -\frac{1}{2} \sin(2x - \pi) + \frac{3}{2}= -\frac{1}{2} \sin(2x + (-\pi)) + \frac{3}{2}\nonumber\]

Encontramos\(A = -\frac{1}{2}\),\(\omega = 2\),\(\phi = -\pi\) y\(B = \frac{3}{2}\). El periodo es entonces\(\frac{2\pi}{2} = \pi\), la amplitud es\(\left| - \frac{1}{2} \right| = \frac{1}{2}\), el desplazamiento de fase es\(-\frac{-\pi}{2} = \frac{\pi}{2}\) (lo que indica un desplazamiento a la derecha\(\frac{\pi}{2}\) unidades) y el desplazamiento vertical es hacia arriba\(\frac{3}{2}\). Tenga en cuenta que, en este caso, todos los datos coinciden con nuestra gráfica de\(y=g(x)\) con la excepción del desplazamiento de fase. [phaseshiftissue] En lugar de que la gráfica empiece en\(x = \frac{\pi}{2}\), termina ahí. Recuerde, sin embargo, que la gráfica presentada en el Ejemplo 10.5.1 es sólo una porción de la gráfica de\(y=g(x)\). En efecto, otro ciclo completo comienza a las\(x = \frac{\pi}{2}\), y este es el ciclo que el Teorema 10.23 está detectando. El motivo de la discrepancia es que, para aplicar el Teorema 10.23, tuvimos que reescribir la fórmula para\(g(x)\) usar la propiedad impar de la función sinusoidal. Tenga en cuenta que ya sea que graficemos\(y=g(x)\) usando el enfoque de 'marcas de cuarto' o usando el Teorema 10.23, obtenemos un ciclo completo de la gráfica, lo que significa que hemos determinado completamente la sinusoide.

Ejemplo 10.5.2

A continuación se muestra la gráfica de un ciclo completo de una sinusoide\(y=f(x)\).

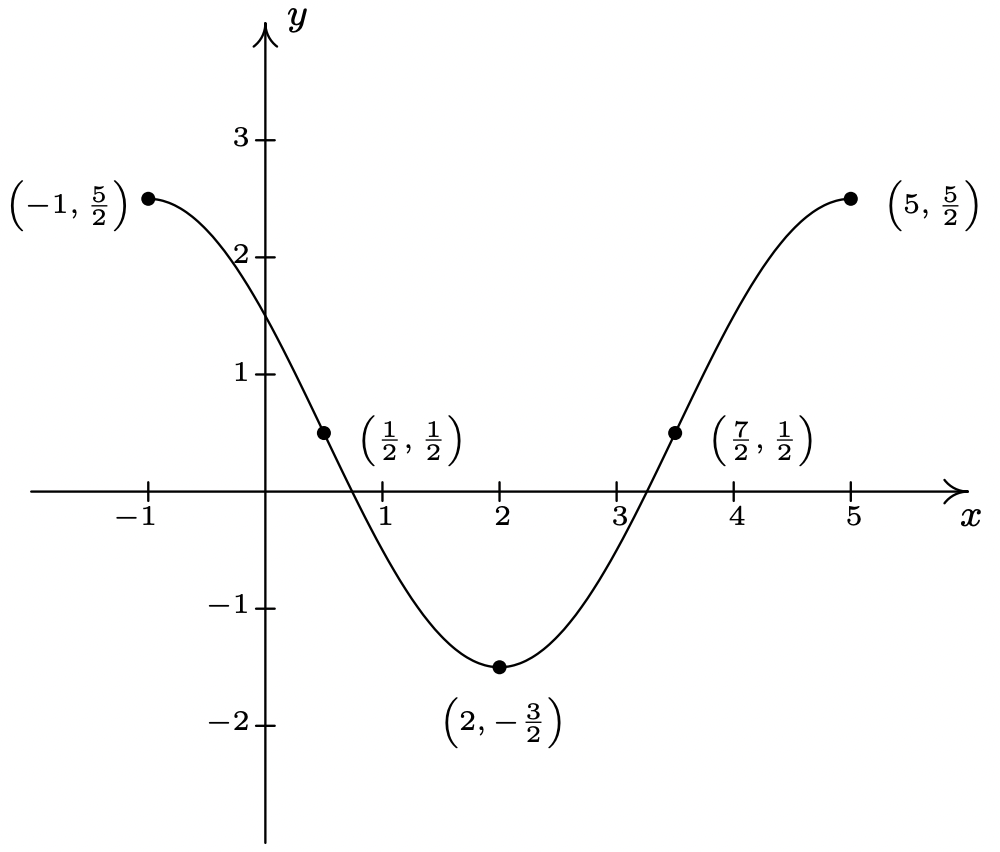
Un ciclo de\(y=f(x)\).

1. Encuentra una función coseno cuya gráfica coincida con la gráfica de\(y = f(x)\).
2. Encuentra una función sinusoidal cuya gráfica coincida con la gráfica de\(y = f(x)\).

Solución.

1. Ajustamos los datos a una función del formulario\(C(x) = A \cos(\omega x + \phi) + B\). Dado que un ciclo se grafica a lo largo del intervalo\([-1,5]\), su periodo es\(5-(-1) = 6\). Según el Teorema 10.23,\(6 = \frac{2\pi}{\omega}\), así que\(\omega = \frac{\pi}{3}\). A continuación, vemos que el cambio de fase es\(-1\), entonces tenemos\(-\frac{\phi}{\omega} = -1\), o\(\phi = \omega = \frac{\pi}{3}\). Para encontrar la amplitud, tenga en cuenta que el rango de la sinusoide es\(\left[ -\frac{3}{2}, \frac{5}{2}\right]\). Como resultado, la amplitud\(A = \frac{1}{2}\left[ \frac{5}{2} - \left(-\frac{3}{2}\right)\right] = \frac{1}{2} (4) = 2.\) Finalmente, para determinar el desplazamiento vertical, promediamos los puntos finales del rango a encontrar\(B = \frac{1}{2}\left[ \frac{5}{2} + \left(-\frac{3}{2}\right)\right] = \frac{1}{2}(1) = \frac{1}{2}\). Nuestra respuesta final es\(C(x) = 2 \cos\left(\frac{\pi}{3} x + \frac{\pi}{3} \right) + \frac{1}{2}\).
2. Se realiza la mayor parte del trabajo para ajustar los datos a una función del formulario\(S(x) = A \sin(\omega x + \phi) + B\). El periodo, amplitud y desplazamiento vertical son los mismos que antes con\(\omega = \frac{\pi}{3}\),\(A = 2\) y\(B = \frac{1}{2}\). La parte más engañosa es encontrar el desplazamiento de fase. Para ello, imaginamos extender la gráfica de la sinusoide dada como en la siguiente figura para que podamos identificar un ciclo que comienza en\(\left(\frac{7}{2}, \frac{1}{2}\right)\). Tomando el cambio de fase para ser\(\frac{7}{2}\), obtenemos\(-\frac{\phi}{\omega} = \frac{7}{2}\), o\(\phi = -\frac{7}{2} \omega = -\frac{7}{2}\left(\frac{\pi}{3}\right) = -\frac{7\pi}{6}\). De ahí que nuestra respuesta sea\(S(x) = 2 \sin\left(\frac{\pi}{3} x - \frac{7\pi}{6}\right) + \frac{1}{2}\).

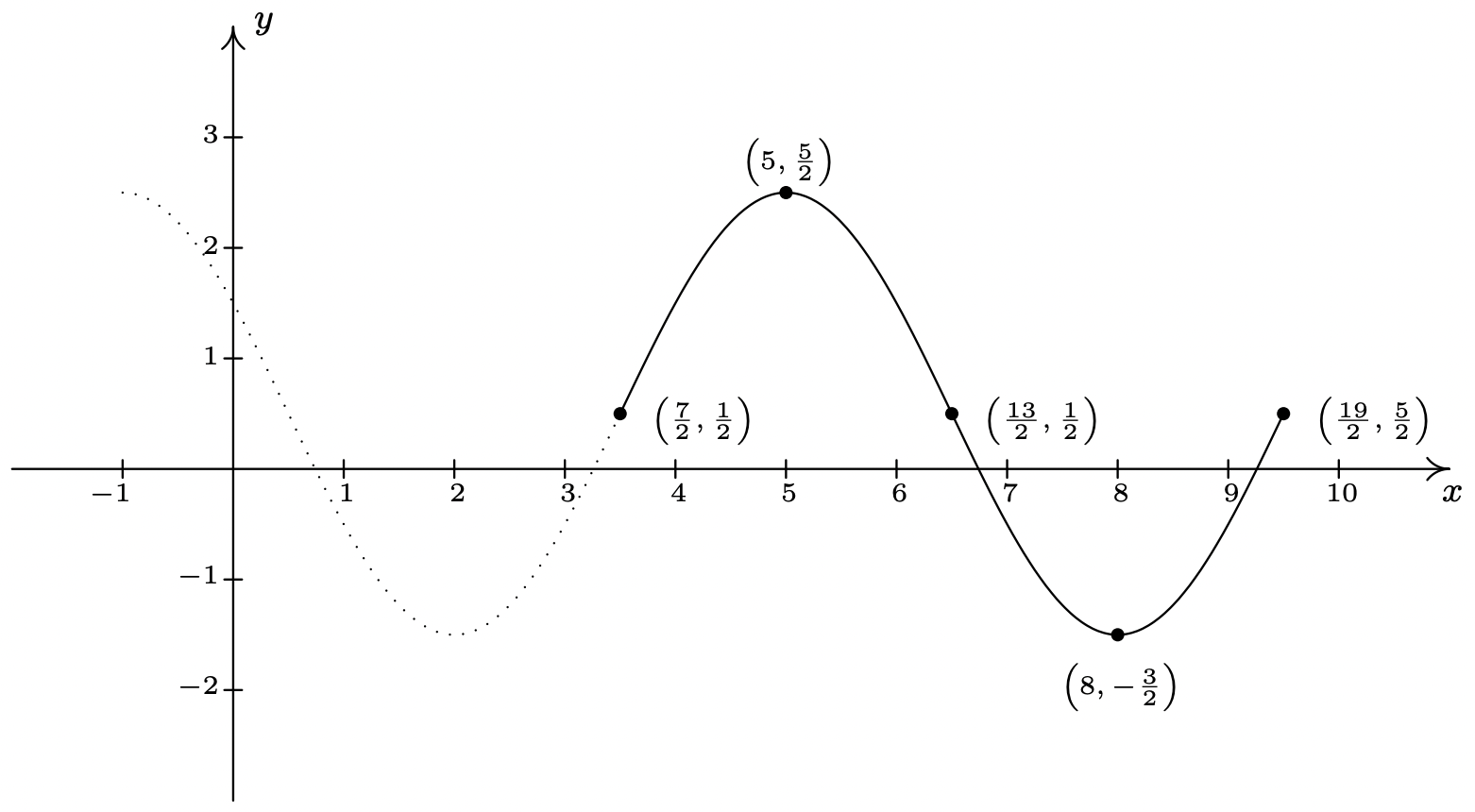Extendiendo la gráfica de\(y=f(x)\).

Tenga en cuenta que cada una de las respuestas dadas en el Ejemplo 10.5.2 es una opción entre muchas respuestas posibles. Por ejemplo, al ajustar una función sinusoidal a los datos, podríamos haber optado por comenzar a\(\left(\frac{1}{2}, \frac{1}{2}\right)\) tomar\(A = -2\). En este caso, el desplazamiento de fase es\(\frac{1}{2}\) así\(\phi = -\frac{\pi}{6}\) para una respuesta de\(S(x) = -2 \sin\left(\frac{\pi}{3} x - \frac{\pi}{6}\right) + \frac{1}{2}\). Alternativamente, podríamos haber extendido la gráfica de\(y=f(x)\) hacia la izquierda y considerar una función sinusoidal a partir de\(\left(-\frac{5}{2}, \frac{1}{2}\right)\), y así sucesivamente. Cada una de estas fórmulas determina la misma curva sinusoidal y sus fórmulas son todas equivalentes usando identidades. Hablando de identidades, si usamos la identidad suma para coseno, podemos expandir la fórmula para producir\[C(x) = A \cos(\omega x + \phi) + B = A\cos(\omega x) \cos(\phi) - A \sin(\omega x)\sin(\phi) + B.\nonumber\] De manera similar, usando la identidad suma para seno, obtenemos\[S(x) = A \sin(\omega x + \phi) + B = A\sin(\omega x) \cos(\phi) + A \cos(\omega x)\sin(\phi) + B.\nonumber\] Hacer estas observaciones nos permite reconocer (y graficar) funciones como sinusoides que, a primera vista, no parecen ajustarse a las formas de ya sea\(C(x)\) o\(S(x)\).

Ejemplo 10.5.3.

Considera la función\(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\). Encuentre una fórmula para\(f(x)\):

1. en el formulario\(C(x) = A \cos(\omega x + \phi) + B\) para\(\omega > 0\)
2. en el formulario\(S(x) = A \sin(\omega x + \phi) + B\) para\(\omega > 0\)

Revisa tus respuestas analíticamente usando identidades y gráficamente usando una calculadora.

Solución.

1. La clave de este problema es utilizar las formas expandidas de las fórmulas sinusoidales y hacer coincidir los coeficientes correspondientes. Equiparando\(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\) con la forma expandida de\(C(x) = A \cos(\omega x + \phi) + B\), obtenemos

   \[\cos(2x) - \sqrt{3} \sin(2x) = A\cos(\omega x) \cos(\phi) - A \sin(\omega x)\sin(\phi) + B\nonumber\]

   Debe quedar claro que podemos tomar\(\omega = 2\) y\(B = 0\) conseguir

   \[\cos(2x) - \sqrt{3} \sin(2x) = A\cos(2x) \cos(\phi) - A \sin(2x)\sin(\phi)\nonumber\]

   Para determinar\(A\) y\(\phi\), se trata de un poco más de trabajo. Comenzamos igualando los coeficientes de las funciones trigonométricas a cada lado de la ecuación. En el lado izquierdo, el coeficiente de\(\cos(2x)\) es\(1\), mientras que en el lado derecho, lo es\(A \cos(\phi)\). Ya que esta ecuación es para sostener para todos los números reales, debemos tener ⁸ eso\(A \cos(\phi) = 1\). De igual manera, encontramos equiparando los coeficientes de\(\sin(2x)\) eso\(A \sin(\phi) = \sqrt{3}\). ¡Lo que tenemos aquí es un sistema de ecuaciones no lineales! Podemos eliminar temporalmente la dependencia de\(\phi\) usando la Identidad Pitagórica. Sabemos\(\cos^{2}(\phi) + \sin^{2}(\phi) = 1\), así multiplicando esto por\(A^2\) da\(A^2\cos^{2}(\phi) + A^2\sin^{2}(\phi) = A^2\). Desde\(A \cos(\phi) = 1\) y\(A \sin(\phi) = \sqrt{3}\), obtenemos\(A^2 = 1^2 + (\sqrt{3})^2 = 4\) o\(A = \pm 2\). Escogiendo\(A = 2\), tenemos\(2\cos(\phi) = 1\) y\(2 \sin(\phi) = \sqrt{3}\) o, después de algún reordenamiento,\(\cos(\phi) = \frac{1}{2}\) y\(\sin(\phi) = \frac{\sqrt{3}}{2}\). Uno de esos ángulos\(\phi\) que satisface este criterio es\(\phi = \frac{\pi}{3}\). De ahí que una forma de escribir\(f(x)\) como sinusoide es\(f(x) = 2 \cos\left(2x + \frac{\pi}{3}\right)\). Podemos verificar fácilmente nuestra respuesta usando la fórmula de suma para coseno\[\begin{array}{rcl} f(x) & = & 2 \cos\left(2x + \frac{\pi}{3}\right) \\[4pt] & = & 2 \left[ \cos(2x) \cos\left(\frac{\pi}{3}\right) - \sin(2x) \sin\left(\frac{\pi}{3}\right) \right]\\[4pt] & = & 2 \left[ \cos(2x) \left(\frac{1}{2}\right) - \sin(2x) \left(\frac{\sqrt{3}}{2}\right)\right] \\[4pt] & = & \cos(2x) - \sqrt{3} \sin(2x) \\ \end{array}\nonumber\]

2. Procediendo como antes, nos equiparamos\(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\) con la forma ampliada de\(S(x) = A \sin(\omega x + \phi) + B\) obtener

   \[\cos(2x) - \sqrt{3} \sin(2x) = A\sin(\omega x) \cos(\phi) + A \cos(\omega x)\sin(\phi) + B\nonumber\]

   Una vez más, podemos tomar\(\omega = 2\) y\(B = 0\) para que

   \[\cos(2x) - \sqrt{3} \sin(2x) = A\sin(2x) \cos(\phi) + A \cos(2x)\sin(\phi)\nonumber\]

   Igualamos ⁹ los coeficientes de\(\cos(2x)\) a cada lado y obtenemos\(A\sin(\phi) = 1\) y\(A\cos(\phi) = -\sqrt{3}\). Usando\(A^2\cos^{2}(\phi) + A^2\sin^{2}(\phi) = A^2\) como antes, obtenemos\(A = \pm 2\), y nuevamente elegimos\(A = 2\). Esto significa\(2 \sin(\phi) = 1\), o\(\sin(\phi) = \frac{1}{2}\), y\(2\cos(\phi) = -\sqrt{3}\), que significa\(\cos(\phi) = -\frac{\sqrt{3}}{2}\). Uno de esos ángulos que cumple con estos criterios es\(\phi = \frac{5\pi}{6}\). De ahí, tenemos\(f(x) = 2 \sin\left(2x + \frac{5\pi}{6}\right)\). Comprobando nuestro trabajo analíticamente, tenemos\[\begin{array}{rcl} f(x) & = & 2 \sin\left(2x + \frac{5\pi}{6}\right) \\[4pt] & = & 2 \left[ \sin(2x) \cos\left(\frac{5\pi}{6}\right) + \cos(2x) \sin\left(\frac{5\pi}{6}\right) \right]\\[4pt] & = & 2 \left[ \sin(2x) \left(-\frac{\sqrt{3}}{2}\right) + \cos(2x) \left(\frac{1}{2}\right)\right] \\[4pt] & = & \cos(2x) - \sqrt{3} \sin(2x) \\ \end{array}\nonumber\] Graficando las tres fórmulas para\(f(x)\) resultado en la curva idéntica, verificando nuestro trabajo analítico.

   

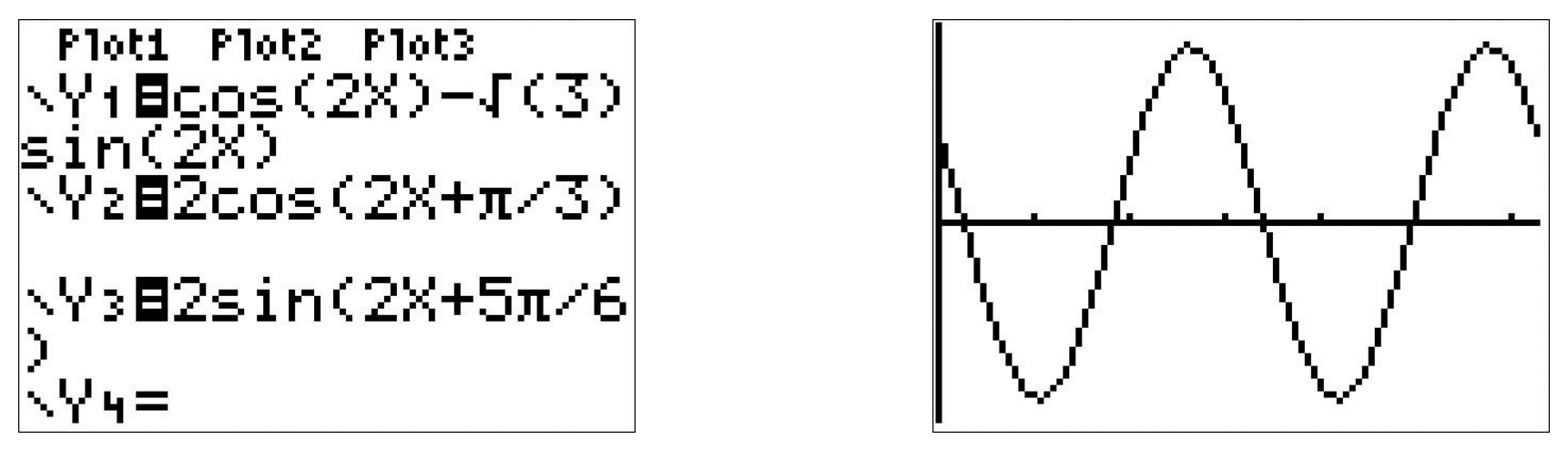
Es importante señalar que para que la técnica presentada en el Ejemplo 10.5.3 ajuste una función en una de las formas del Teorema 10.23, los argumentos de la función coseno y seno coinciden mucho. Es decir, mientras\(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\) sea sinusoide, no\(g(x) = \cos(2x) - \sqrt{3} \sin(3x)\) lo es. ¹⁰ También vale la pena mencionar que, si hubiéramos elegido\(A = -2\) en lugar de\(A = 2\) como trabajamos a través del Ejemplo 10.5.3, nuestras respuestas finales se habrían visto diferentes. Se anima al lector a reelaborar el Ejemplo 10.5.3 usando\(A = -2\) para ver cuáles son estas diferencias, y luego para un ejercicio desafiante, usar identidades para demostrar que todas las fórmulas son equivalentes. Las ecuaciones generales para ajustar una función de la forma\(f(x) = a \, \cos(\omega x) + b \, \sin(\omega x) + B\) en una de las formas del Teorema 10.23 se exploran en el Ejercicio 35.

10.5.2. Gráficas de las Funciones Secante y Cosecante

Ahora dirigimos nuestra atención a la gráfica\(y = \sec(x)\). Ya que\(\sec(x) = \frac{1}{\cos(x)}\), podemos utilizar nuestra tabla de valores para la gráfica de\(y = \cos(x)\) y tomar recíprocos. Sabemos por la Sección 10.3.1 que el dominio de\(F(x) = \sec(x)\) excluye todos los múltiplos impares de\(\frac{\pi}{2}\), y efectivamente, nos encontramos con problemas en\(x = \frac{\pi}{2}\) y\(x = \frac{3\pi}{2}\) desde entonces\(\cos(x) = 0\) a estos valores. Utilizando la notación introducida en la Sección 4.2, tenemos eso como\(x \rightarrow \frac{\pi}{2}^{-}\),\(\cos(x) \rightarrow 0^{+}\), entonces\(\sec(x) \rightarrow \infty\). (Ver Sección 10.3.1 para un análisis más detallado.) De igual manera, encontramos que como\(x \rightarrow \frac{\pi}{2}^{+}\),\(\sec(x) \rightarrow -\infty\); como\(x \rightarrow \frac{3\pi}{2}^{-}\),\(\sec(x) \rightarrow -\infty\); y como\(x \rightarrow \frac{3\pi}{2}^{+}\),\(\sec(x) \rightarrow \infty\). Esto significa que tenemos un par de asíntotas verticales a la gráfica de\(y = \sec(x)\),\(x = \frac{\pi}{2}\) y\(x = \frac{3\pi}{2}\). Ya que\(\cos(x)\) es periódico con periodo\(2\pi\), se deduce que también\(\sec(x)\) es. ¹¹ A continuación graficamos un ciclo fundamental de\(y = \sec(x)\) junto con una gráfica más completa obtenida por el habitual 'copiado y pegado'. ¹²

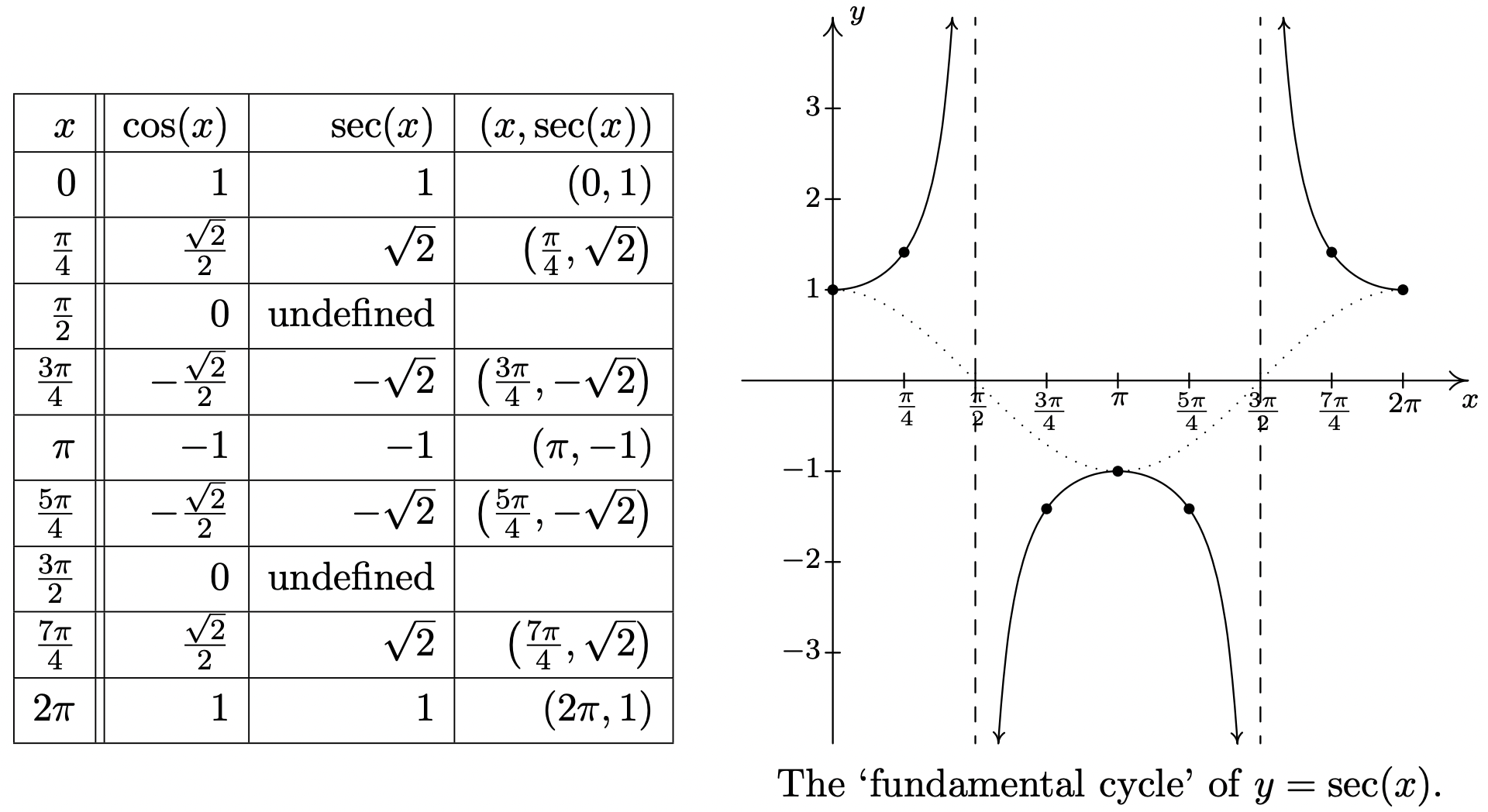
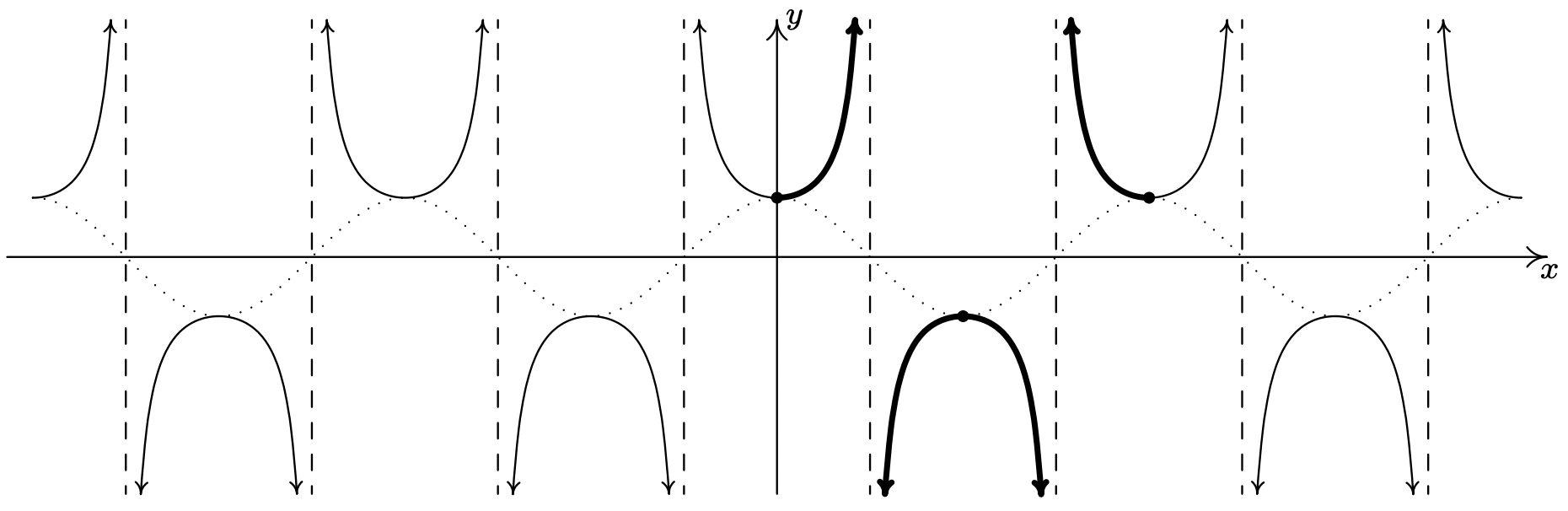
La gráfica de\(y=\sec (x)\).

Como cabría esperar, para graficar\(y = \csc(x)\) comenzamos\(y = \sin(x)\) y tomamos recíprocos de los\(y\) valores correspondientes. Aquí, encontramos problemas en\(x = 0\),\(x = \pi\) y\(x = 2\pi\). Procediendo con el análisis habitual, graficamos el ciclo fundamental de\(y = \csc(x)\) abajo junto con la gráfica punteada de\(y=\sin(x)\) para referencia. Ya que\(y = \sin(x)\) y\(y = \cos(x)\) son meramente cambios de fase entre sí, también lo son\(y = \csc(x)\) y\(y = \sec(x)\).

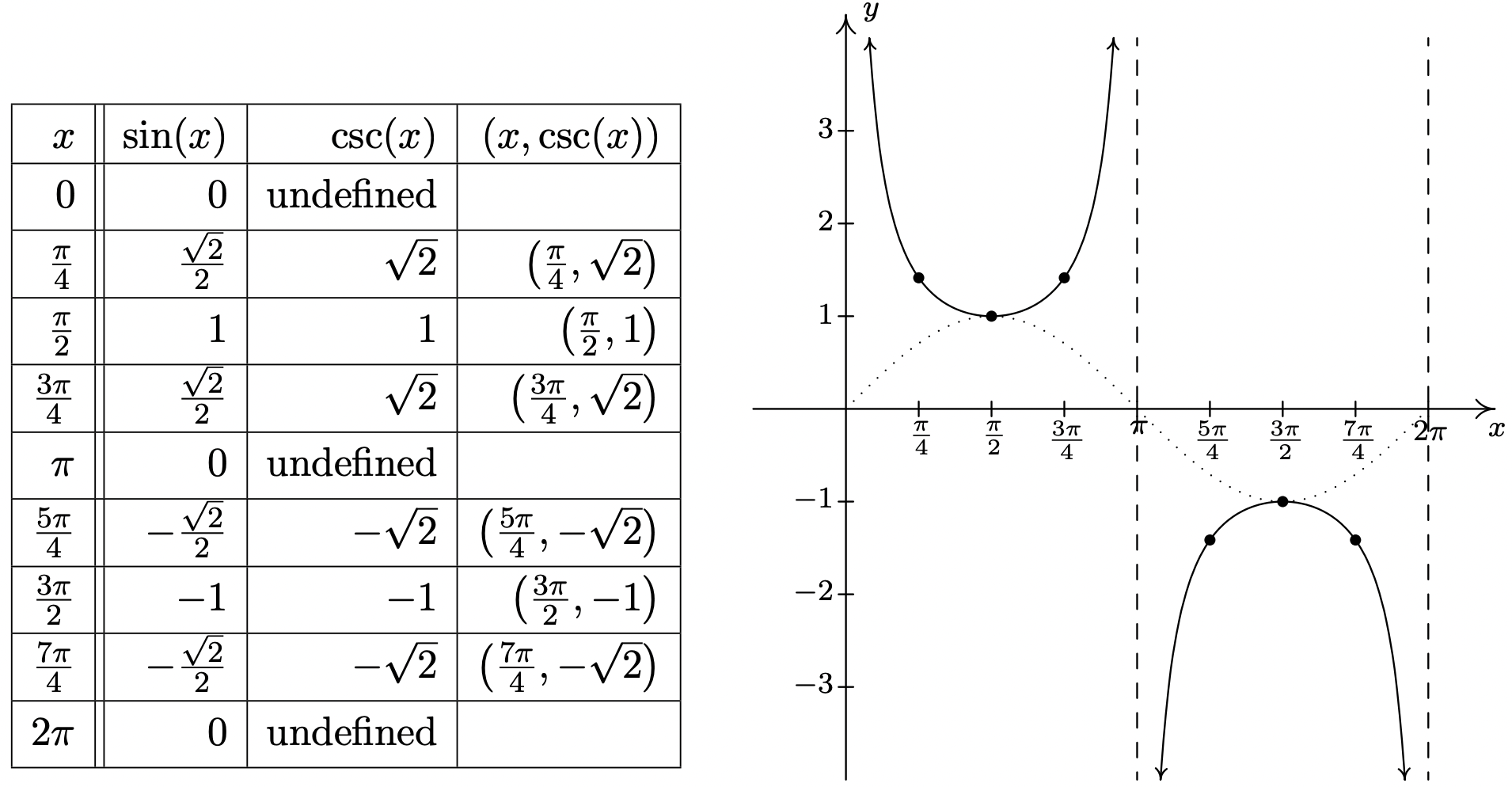
El 'ciclo fundamental' de\(y=\csc (x)\).

Una vez más, nuestro trabajo de dominio y rango en la Sección 10.3.1 se verifica geométricamente en la gráfica de\(y = G(x) = \csc(x)\).

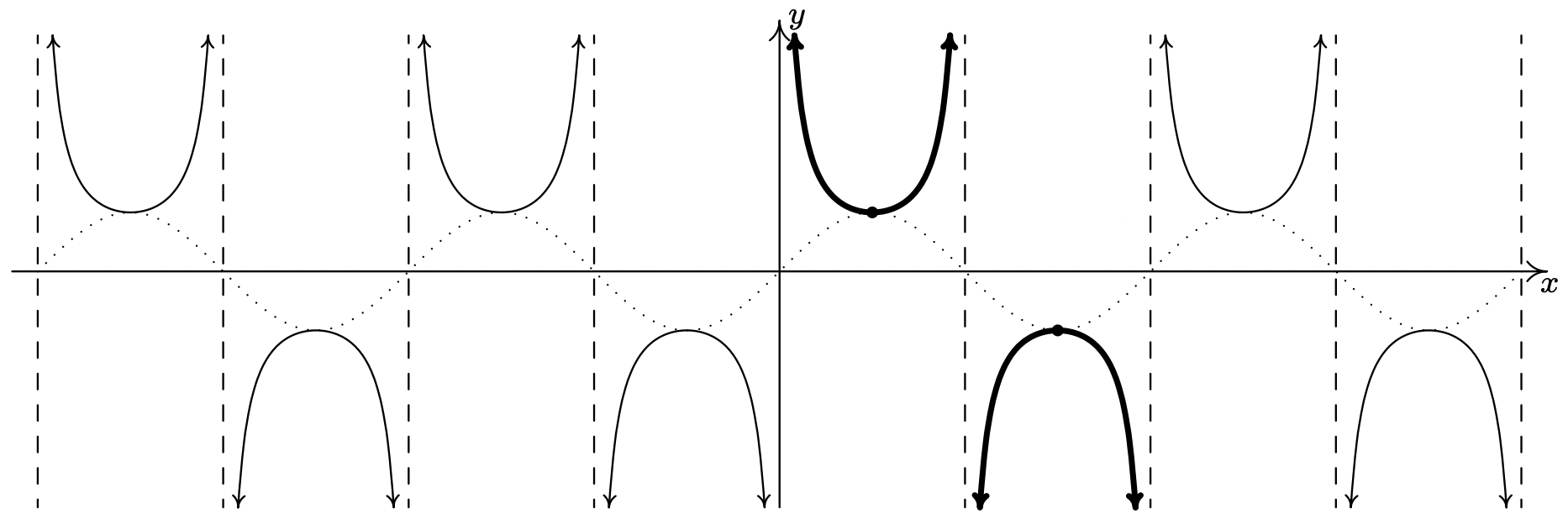
La gráfica de\(y=\csc (x)\).

Obsérvese que, en los intervalos entre las asíntotas verticales, ambas\(F(x) = \sec(x)\) y\(G(x) = \csc(x)\) son continuas y lisas. En otras palabras, son continuos y suaves en sus dominios. ¹³ El siguiente teorema resume las propiedades de las funciones secante y cosecante. Obsérvese que todas estas propiedades son resultado directo de que son recíprocas de las funciones coseno y seno, respectivamente.

Teorema 10.24. Propiedades de las Funciones Secante y Cosecante

• La función\(F(x) = \sec(x)\)
  • tiene dominio\(\left\{x: x \neq \frac{\pi}{2}+\pi k, k \text { is an integer }\right\}=\bigcup_{k=-\infty}^{\infty}\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\)
  • tiene rango\(\{ y : |y| \geq 1 \} = (-\infty, -1] \cup [1, \infty)\)
  • es continuo y suave en su dominio
  • es parejo
  • tiene periodo\(2\pi\)
• La función\(G(x) = \csc(x)\)
  • tiene dominio\(\{x: x \neq \pi k, k \text { is an integer }\}=\bigcup_{k=-\infty}^{\infty}(k \pi,(k+1) \pi)\)
  • tiene rango\(\{ y : |y| \geq 1 \} = (-\infty, -1] \cup [1, \infty)\)
  • es continuo y suave en su dominio
  • es impar
  • tiene periodo\(2\pi\)

En el siguiente ejemplo, discutimos graficar curvas secantes y cosecantes más generales.

Ejemplo 10.5.4

Grafique un ciclo de las siguientes funciones. Indicar el periodo de cada uno.

1. \(f(x) = 1 - 2 \sec(2x)\)
2. \(g(x) = \dfrac{\csc(\pi - \pi x) - 5}{3}\)

Solución.

1. Para graficar\(y = 1 - 2 \sec(2x)\), seguimos el mismo procedimiento que en el Ejemplo 10.5.1. Primero, establecemos el argumento de secante,\(2x\), igual a los 'cuartos de marca'\(0\)\(\frac{\pi}{2}\),\(\pi\),\(\frac{3\pi}{2}\)\(2\pi\) y resolvemos para\(x\).

   \[\begin{array}{|r|r|r|} \hline a & 2 x=a & x \\ \hline 0 & 2 x=0 & 0 \\ \hline \frac{\pi}{2} & 2 x=\frac{\pi}{2} & \frac{\pi}{4} \\ \hline \pi & 2 x=\pi & \frac{\pi}{2} \\ \hline \frac{3 \pi}{2} & 2 x=\frac{3 \pi}{2} & \frac{3 \pi}{4} \\ \hline 2 \pi & 2 x=2 \pi & \pi \\ \hline \end{array}\nonumber\]

   A continuación, sustituimos estos\(x\) valores en\(f(x)\). Si\(f(x)\) existe, tenemos un punto en la gráfica; de lo contrario, hemos encontrado una asíntota vertical. Además de estos puntos y asíntotas, hemos graficado la curva coseno asociada —en este caso\(y = 1 - 2 \cos(2x)\) — punteada en la imagen de abajo. Dado que un ciclo se grafica a lo largo del intervalo\([0,\pi]\), el periodo es\(\pi - 0 = \pi\).

   

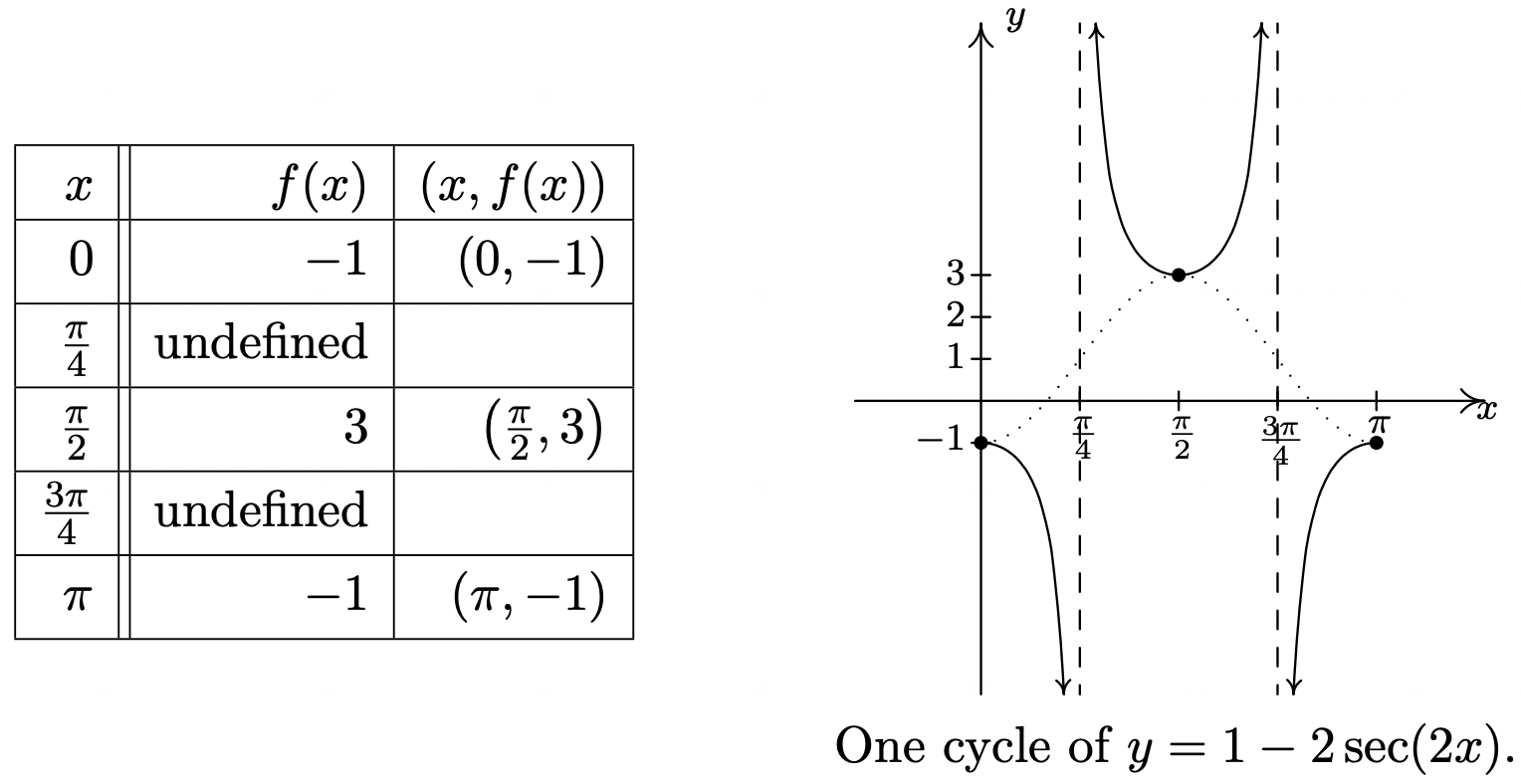
2. Procediendo como antes, establecemos el argumento de cosecante en\(g(x) = \frac{\csc(\pi - \pi x) - 5}{3}\) igual a las marcas de cuarto y resolvemos para\(x\).

   \[\begin{array}{|r|r|r|} \hline a & \pi-\pi x=a & x \\ \hline 0 & \pi-\pi x=0 & 1 \\ \hline \frac{\pi}{2} & \pi-\pi x=\frac{\pi}{2} & \frac{1}{2} \\ \hline \pi & \pi-\pi x=\pi & 0 \\ \hline \frac{3 \pi}{2} & \pi-\pi x=\frac{3 \pi}{2} & -\frac{1}{2} \\ \hline 2 \pi & \pi-\pi x=2 \pi & -1 \\ \hline \end{array}\nonumber\]

   Sustituyendo estos\(x\) -valores en\(g(x)\), generamos la gráfica a continuación y encontramos el periodo a ser\(1 - (-1) = 2\). La curva sinusoidal asociada\(y = \frac{\sin(\pi - \pi x) - 5}{3}\),, está punteada como referencia.

   

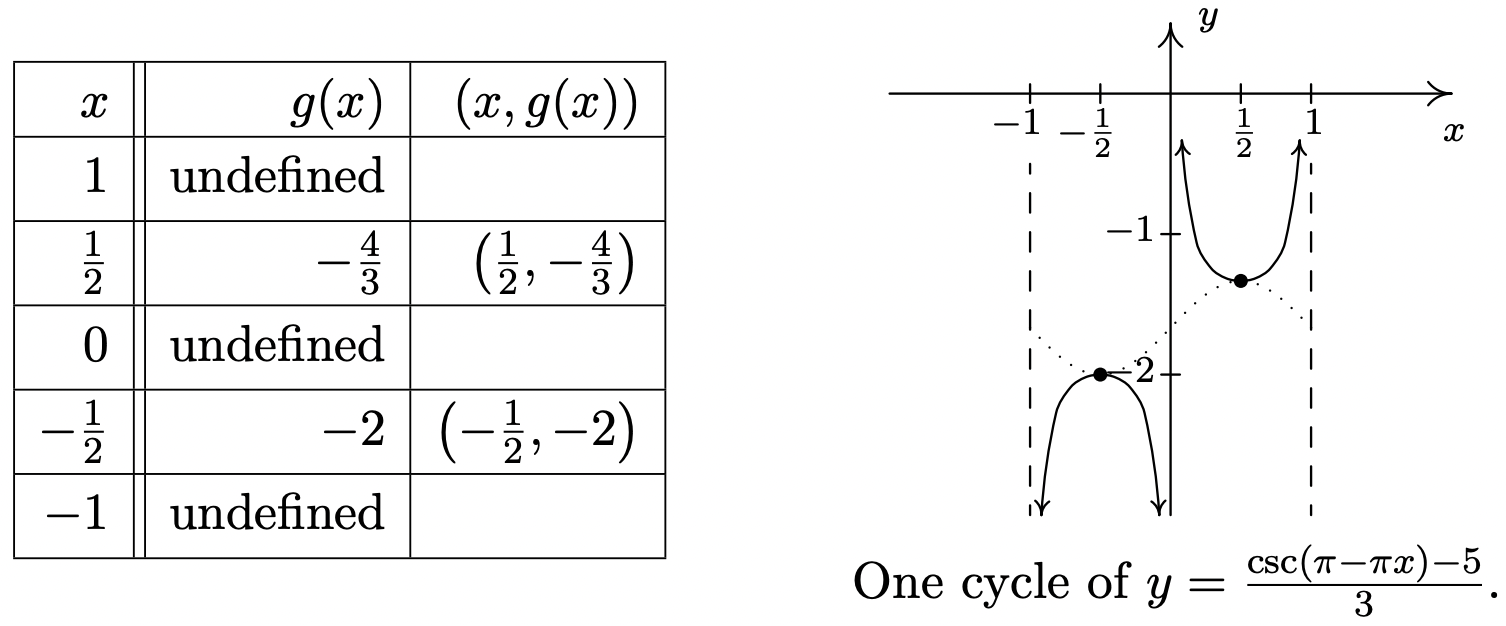
Antes de continuar, observamos que es posible hablar del periodo, desplazamiento de fase y desplazamiento vertical de las gráficas secantes y cosecantes y usar identidades pares/impares para ponerlas en una forma similar a las formas sinusoidales mencionadas en el Teorema 10.23. Dado que estas cantidades coinciden con las de las curvas coseno y seno correspondientes, no lo explicamos explícitamente. Finalmente, dado que los rangos de secante y cosecante no están acotados, no hay amplitud asociada a estas curvas.

10.5.3. Gráficas de las Funciones Tangente y Cotangente

Finalmente, volvemos nuestra atención a las gráficas de las funciones tangente y cotangente. Al construir una tabla de valores para la función tangente, vemos que no\(J(x) = \tan(x)\) está definida en\(x = \frac{\pi}{2}\) y\(x = \frac{3\pi}{2}\), de acuerdo con nuestros hallazgos en la Sección 10.3.1. Como\(x \rightarrow \frac{\pi}{2}^{-}\),\(\sin(x) \rightarrow 1^{-}\) y\(\cos(x) \rightarrow 0^{+}\), para que la\(\tan(x) = \frac{\sin(x)}{\cos(x)}\rightarrow \infty\) producción de una asíntota vertical en\(x = \frac{\pi}{2}\). Usando un análisis similar, obtenemos eso como\(x \rightarrow \frac{\pi}{2}^{+}\),\(\tan(x) \rightarrow -\infty\); as\(x \rightarrow \frac{3\pi}{2}^{-}\),\(\tan(x) \rightarrow \infty\); y como\(x \rightarrow \frac{3\pi}{2}^{+}\),\(\tan(x) \rightarrow -\infty\). Trazar esta información y realizar el 'copiar y pegar' habitual produce:

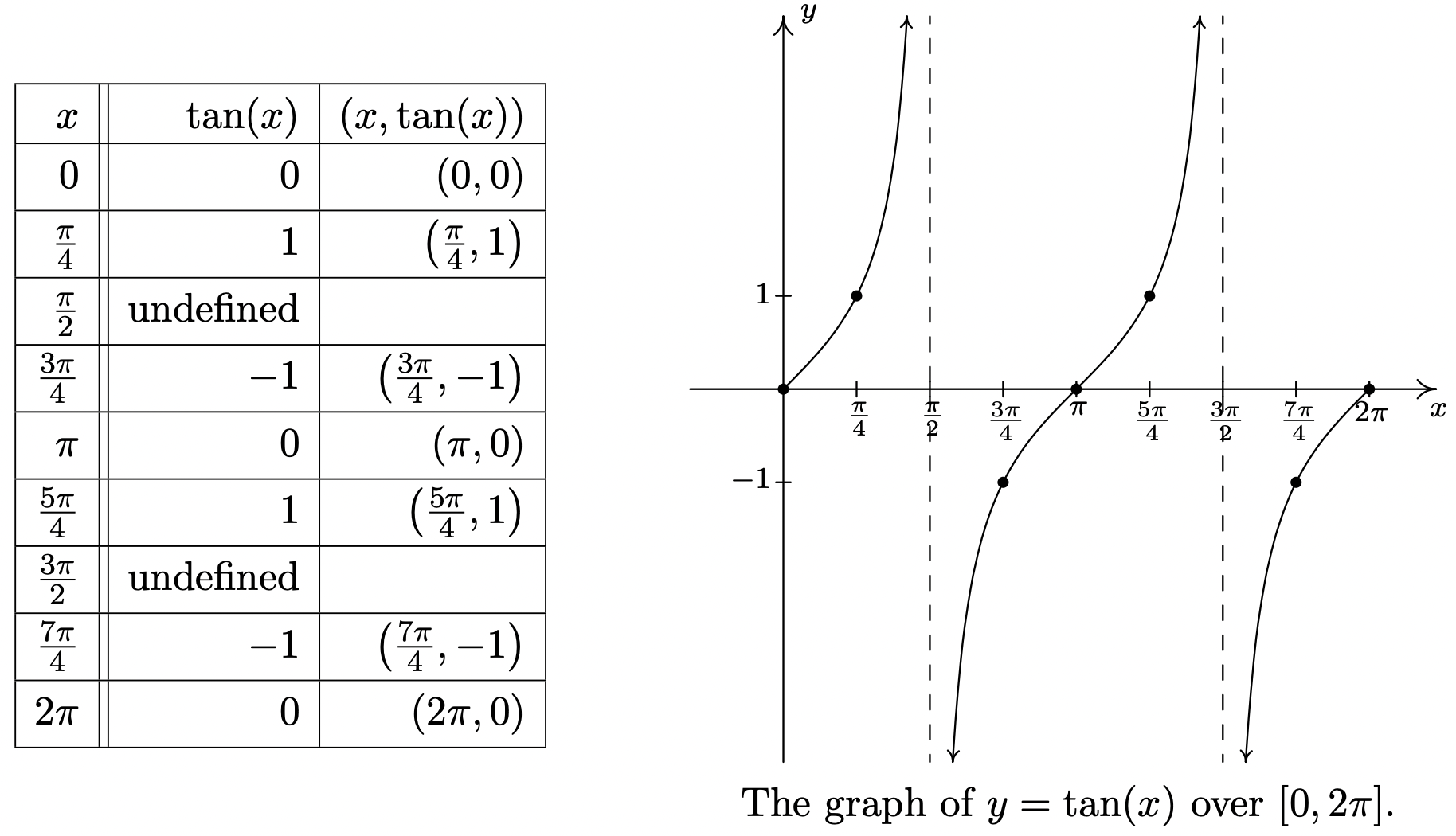
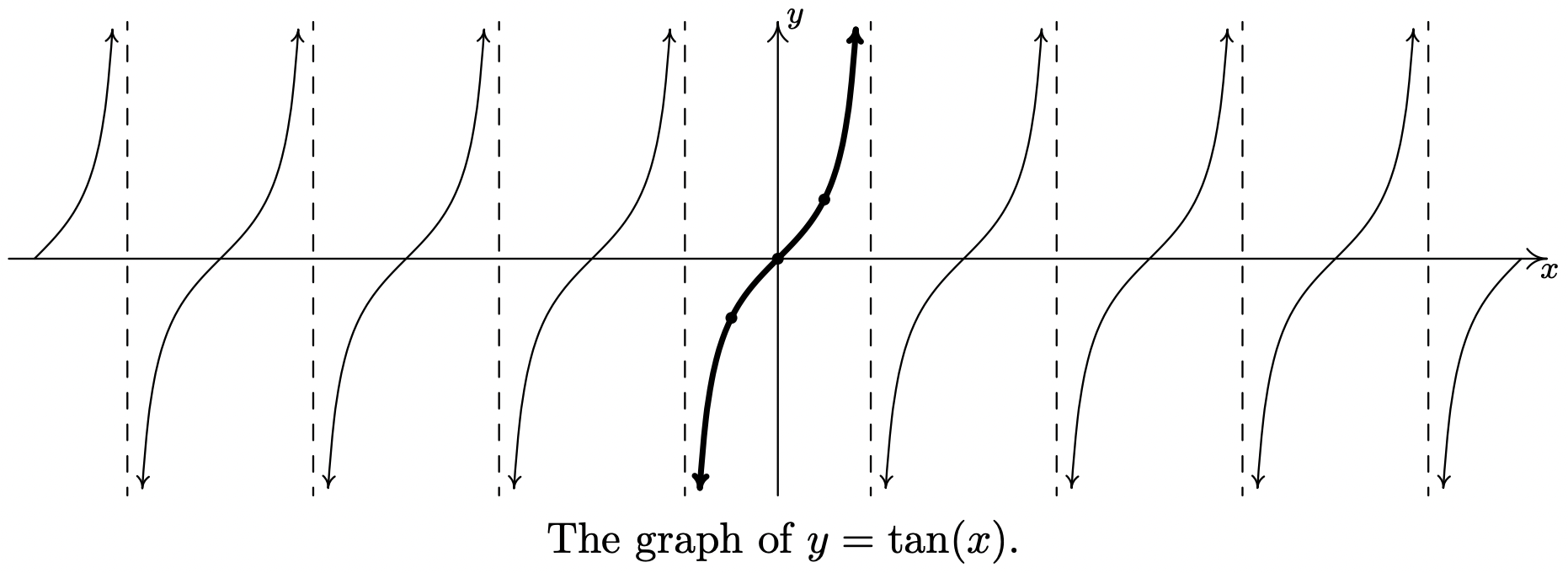
De la gráfica, aparece como si la función tangente fuera periódica con punto\(\pi\). Para probar que así es, apelamos a la fórmula de suma para tangentes. Contamos con:\[\tan(x+\pi) = \dfrac{\tan(x) + \tan(\pi)}{1 - \tan(x) \tan(\pi)} = \dfrac{\tan(x) + 0}{1 - (\tan(x) )(0)} = \tan(x),\nonumber\]

que nos dice que el periodo de\(\tan(x)\) es como mucho\(\pi\). Para demostrar que es exactamente\(\pi\), supongamos que\(p\) es un número real positivo\(\tan(x+p) = \tan(x)\) para que para todos los números reales\(x\). Porque\(x=0\), tenemos\(\tan(p) = \tan(0+p) = \tan(0) = 0\), lo que significa que\(p\) es un múltiplo de\(\pi\). El múltiplo positivo más pequeño de\(\pi\) es\(\pi\) en sí mismo, por lo que hemos establecido el resultado. Tomamos como nuestro ciclo fundamental para\(y=\tan(x)\) el intervalo\(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\), y usamos como nuestras 'marcas de cuarto'\(x = -\frac{\pi}{2}\)\(-\frac{\pi}{4}\),\(0\),\(\frac{\pi}{4}\) y\(\frac{\pi}{2}\). A partir de la gráfica, vemos la confirmación de nuestro trabajo de dominio y rango en la Sección 10.3.1.

No debería sorprender que se\(K(x) = \cot(x)\) comporte de manera similar a\(J(x) = \tan(x)\). El trazado a\(\cot(x)\) lo largo del intervalo\([0,2\pi]\) da como resultado la siguiente gráfica.

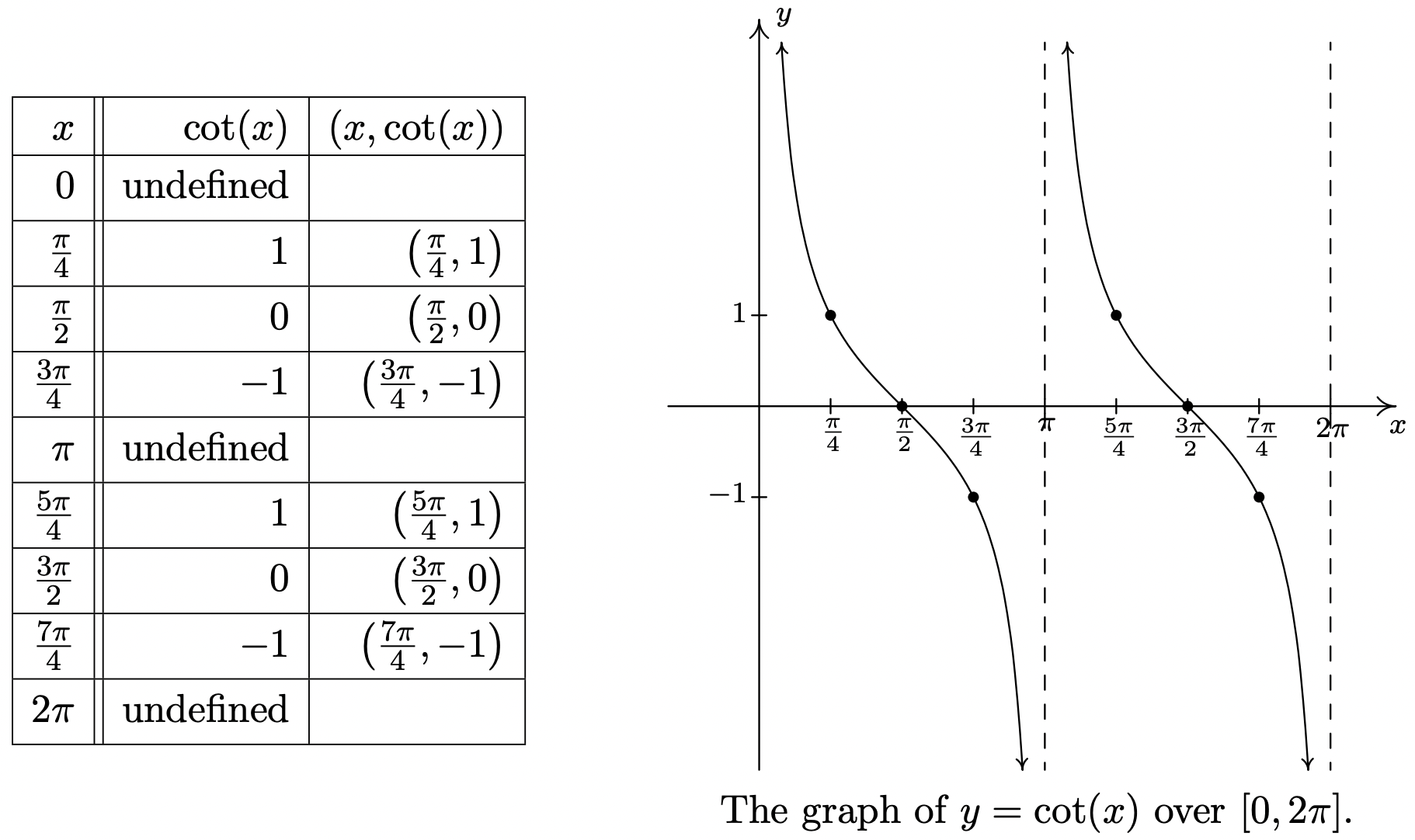
A partir de estos datos, aparece claramente como si el periodo de\(\cot(x)\) es\(\pi\), y dejamos que el lector lo demuestre. ¹⁴ Tomamos como ciclo fundamental el intervalo\((0,\pi)\) con marcas de cuartos:\(x= 0\),\(\frac{\pi}{4}\),\(\frac{\pi}{2}\),\(\frac{3\pi}{4}\) y\(\pi\). A continuación\(y=\cot(x)\) se muestra una gráfica más completa, junto con el ciclo fundamental resaltado como de costumbre. Una vez más, vemos que el dominio y rango de\(K(x) = \cot(x)\) como se lee en la gráfica coincide con lo que encontramos analíticamente en la Sección 10.3.1.

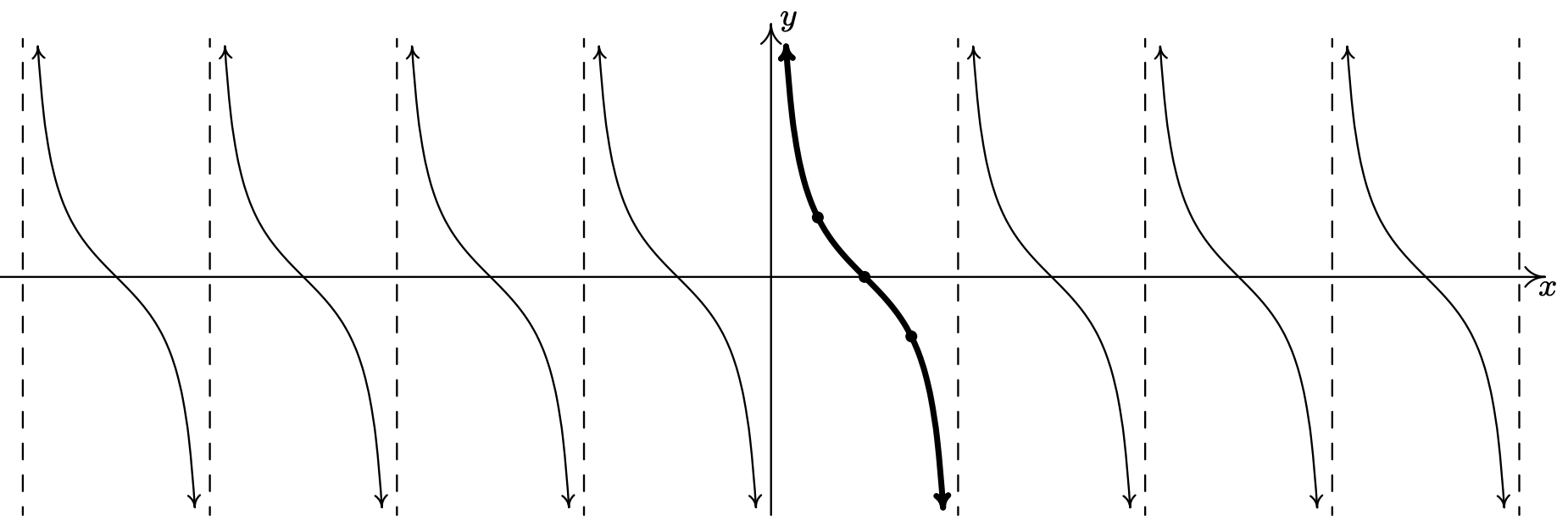
La gráfica de\(y=\cot (x)\).

A continuación se resumen las propiedades de las funciones tangente y cotangente. Al igual que con el Teorema 10.24, cada uno de los resultados a continuación se remonta a las propiedades de las funciones coseno y seno y la definición de las funciones tangente y cotangente como cocientes de las mismas.

Teorema 10.25. Propiedades de las Funciones Tangente y Cotangente

• La función\(J(x) = \tan(x)\)
  • tiene dominio\(\left\{x: x \neq \frac{\pi}{2}+\pi k, k \text { is an integer }\right\}=\bigcup_{k=-\infty}^{\infty}\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\)
  • tiene rango\((-\infty, \infty)\)
  • es continuo y suave en su dominio
  • es impar
  • tiene periodo\(\pi\)
• La función\(K(x) = \cot(x)\)
  • tiene dominio\(\{x: x \neq \pi k, k \text { is an integer }\}=\bigcup_{k=-\infty}^{\infty}(k \pi,(k+1) \pi)\)
  • tiene rango\((-\infty, \infty)\)
  • es continuo y suave en su dominio
  • es impar
  • tiene periodo\(\pi\)

Ejemplo 10.5.5

Grafique un ciclo de las siguientes funciones. Encuentra el periodo.

1. \(f(x) = 1 - \tan\left(\frac{x}{2}\right)\).
2. \(g(x) = 2\cot\left(\frac{\pi}{2} x + \pi\right) + 1\).

Solución.

1. Procedemos como lo hemos hecho en todos los ejemplos gráficos anteriores estableciendo el argumento de tangente en\(f(x) = 1 - \tan\left(\frac{x}{2}\right)\), es decir\(\frac{x}{2}\), igual a cada una de las 'marcas de cuarto'\(-\frac{\pi}{2}\),\(-\frac{\pi}{4}\),\(0\),\(\frac{\pi}{4}\) y\(\frac{\pi}{2}\), y resolviendo para\(x\).

   \[\begin{array}{|r|r|r|} \hline a & \frac{x}{2}=a & x \\ \hline-\frac{\pi}{2} & \frac{x}{2}=-\frac{\pi}{2} & -\pi \\ \hline-\frac{\pi}{4} & \frac{x}{2}=-\frac{\pi}{4} & -\frac{\pi}{2} \\ \hline 0 & \frac{x}{2}=0 & 0 \\ \hline \frac{\pi}{4} & \frac{x}{2}=\frac{\pi}{4} & \frac{\pi}{2} \\ \hline \frac{\pi}{2} & \frac{x}{2}=\frac{\pi}{2} & \pi \\ \hline \end{array}\nonumber\]

   Sustituyendo estos\(x\) valores en\(f(x)\), encontramos puntos en la gráfica y las asíntotas verticales.

   

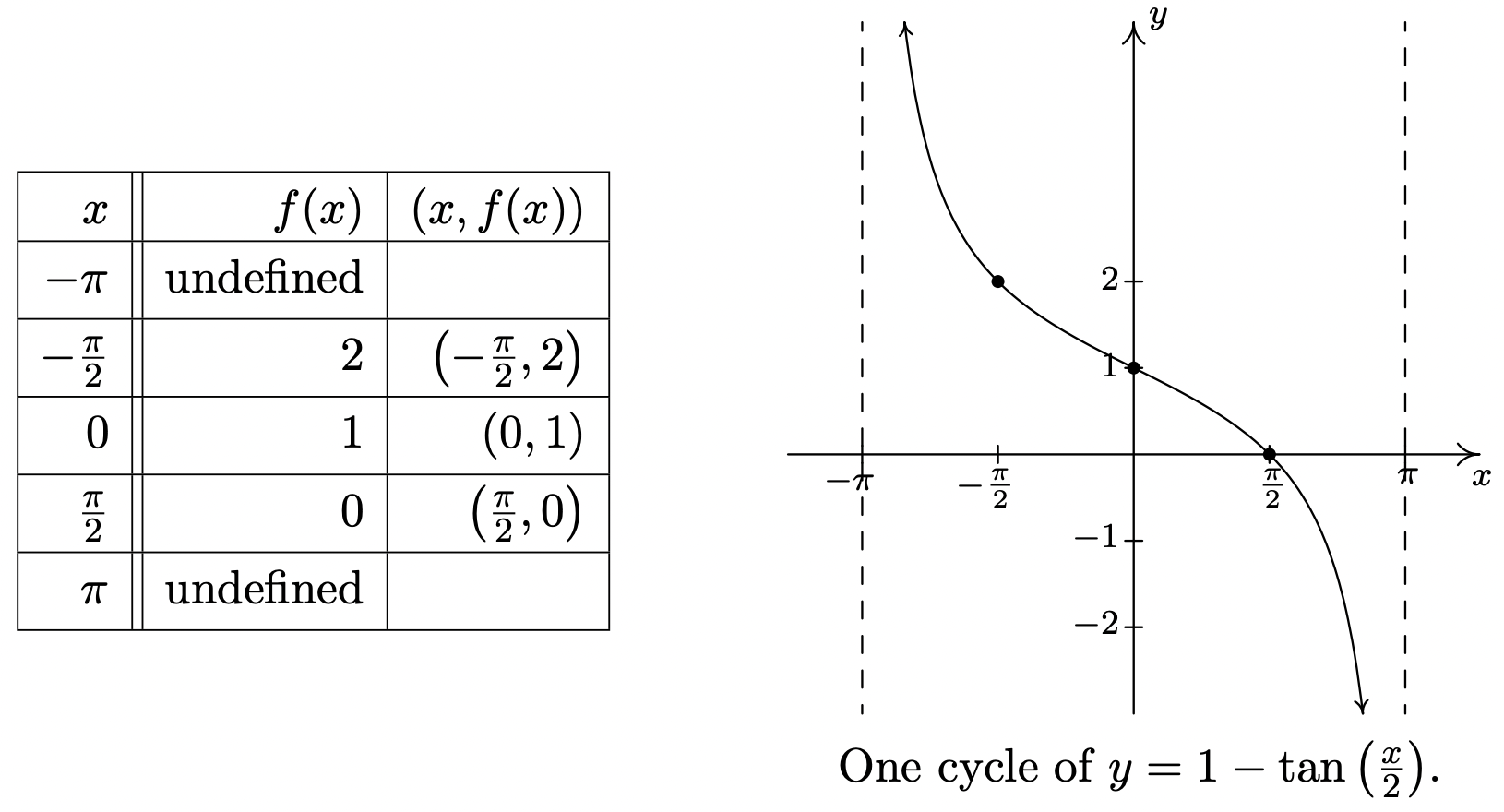
   Vemos que el periodo es\(\pi - (-\pi) = 2\pi\).

2. Las 'marcas de cuarto' para el ciclo fundamental de la curva cotangente son\(0\),\(\frac{\pi}{4}\),\(\frac{\pi}{2}\),\(\frac{3\pi}{4}\) y\(\pi\). Para graficar\(g(x) = 2\cot\left(\frac{\pi}{2} x + \pi\right) + 1\), comenzamos estableciendo\(\frac{\pi}{2} x + \pi\) igual a cada marca de trimestre y resolviendo para\(x\).

   \[\begin{array}{|r|c|r|} \hline a & \frac{\pi}{2} x+\pi=a & x \\ \hline 0 & \frac{\pi}{2} x+\pi=0 & -2 \\ \hline \frac{\pi}{4} & \frac{\pi}{2} x+\pi=\frac{\pi}{4} & -\frac{3}{2} \\ \hline \frac{\pi}{2} & \frac{\pi}{2} x+\pi=\frac{\pi}{2} & -1 \\ \hline \frac{3 \pi}{4} & \frac{\pi}{2} x+\pi=\frac{3 \pi}{4} & -\frac{1}{2} \\ \hline \pi & \frac{\pi}{2} x+\pi=\pi & 0 \\ \hline \end{array}\nonumber\]

   Ahora usamos estos\(x\) -valores para generar nuestra gráfica.

   

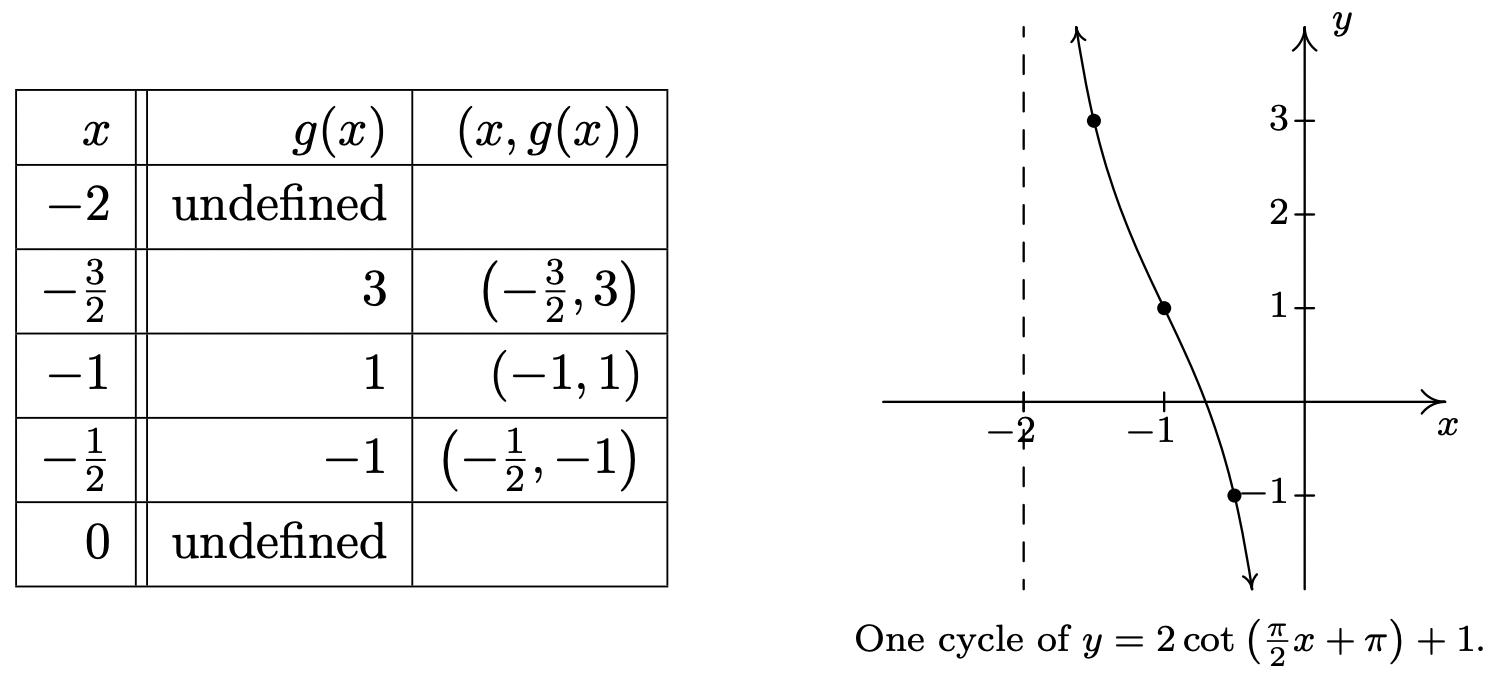
Al igual que con las funciones secante y cosecante, es posible extender la noción de periodo, desplazamiento de fase y desplazamiento vertical a las funciones tangente y cotangente como hicimos para las funciones coseno y seno en el Teorema 10.23. Dado que el número de aplicaciones clásicas que involucran sinusoides supera con creces a las que involucran funciones tangentes y cotangentes, omitimos esto. Se invita al lector ambicioso a formular tal teorema, sin embargo.

10.5.4 Ejercicios

En Ejercicios 1 - 24, grafica un ciclo de la función dada. Indicar el periodo, amplitud, desplazamiento de fase y desplazamiento vertical de la función.

1. \(y = 3\sin(x)\)
2. \(y = \sin(3x)\)
3. \(y = -2\cos(x)\)
4. \(y = \cos \left( x - \dfrac{\pi}{2} \right)\)
5. \(y = -\sin \left( x + \dfrac{\pi}{3} \right)\)
6. \(y = \sin(2x - \pi)\)
7. \(y = -\dfrac{1}{3}\cos \left( \dfrac{1}{2}x + \dfrac{\pi}{3} \right)\)
8. \(y = \cos (3x - 2\pi) + 4\)
9. \(y = \sin \left( -x - \dfrac{\pi}{4} \right) - 2\)
10. \(y = \dfrac{2}{3} \cos \left( \dfrac{\pi}{2} - 4x \right) + 1\)
11. \(y = -\dfrac{3}{2} \cos \left( 2x + \dfrac{\pi}{3} \right) - \dfrac{1}{2}\)
12. \(y = 4\sin (-2\pi x + \pi)\)

En Ejercicios 13 - 24, grafica un ciclo de la función dada. Indicar el periodo de la función.

13. \(y = \tan \left(x - \dfrac{\pi}{3} \right)\)
14. \(y = 2\tan \left( \dfrac{1}{4}x \right) - 3\)
15. \(y = \dfrac{1}{3}\tan(-2x - \pi) + 1\)
16. \(y = \sec \left( x - \dfrac{\pi}{2} \right)\)
17. \(y = -\csc \left( x + \dfrac{\pi}{3} \right)\)
18. \(y = -\dfrac{1}{3} \sec \left( \dfrac{1}{2}x + \dfrac{\pi}{3} \right)\)
19. \(y = \csc (2x - \pi)\)
20. \(y = \sec(3x - 2\pi) + 4\)
21. \(y = \csc \left( -x - \dfrac{\pi}{4} \right) - 2\)
22. \(y = \cot \left( x + \dfrac{\pi}{6} \right)\)
23. \(y = -11\cot \left( \dfrac{1}{5} x \right)\)
24. \(y = \dfrac{1}{3} \cot \left( 2x + \dfrac{3\pi}{2} \right) + 1\)

En Ejercicios 25 - 34, use el Ejemplo 10.5.3 como guía para mostrar que la función es una sinusoide reescribiéndola en las formas\(C(x) = A \cos(\omega x + \phi) + B\) y\(S(x) = A \sin(\omega x + \phi) + B\) para\(\omega > 0\) y\(0 \leq \phi < 2\pi\).

25. \(f(x) = \sqrt{2}\sin(x) + \sqrt{2}\cos(x) + 1\)
26. \(f(x) = 3\sqrt{3}\sin(3x) - 3\cos(3x)\)
27. \(f(x) = -\sin(x) + \cos(x) - 2\)
28. \(f(x) = -\dfrac{1}{2}\sin(2x) - \dfrac{\sqrt{3}}{2}\cos(2x)\)
29. \(f(x) = 2\sqrt{3} \cos(x) - 2\sin(x)\)
30. \(f(x) = \dfrac{3}{2} \cos(2x) - \dfrac{3\sqrt{3}}{2} \sin(2x) + 6\)
31. \(f(x) = -\dfrac{1}{2} \cos(5x) -\dfrac{\sqrt{3}}{2} \sin(5x)\)
32. \(f(x) = -6\sqrt{3} \cos(3x) - 6\sin(3x) - 3\)
33. \(f(x) = \dfrac{5\sqrt{2}}{2} \sin(x) -\dfrac{5\sqrt{2}}{2} \cos(x)\)
34. \(f(x) =3 \sin \left(\dfrac{x}{6}\right) -3\sqrt{3} \cos \left(\dfrac{x}{6}\right)\)
35. En Ejercicios 25 - 34, deberías haber notado una relación entre las fases\(\phi\) para el\(S(x)\) y\(C(x)\). \(f(x) = A \sin(\omega x + \alpha) + B\)Demuéstralo si, entonces\(f(x) = A \cos(\omega x + \beta) + B\) donde\(\beta = \alpha - \dfrac{\pi}{2}\).
36. Dejar\(\phi\) ser un ángulo medido en radianes y dejar\(P(a,b)\) ser un punto en el lado terminal de\(\phi\) cuando se dibuja en posición estándar. Utilice el Teorema 10.3 y la suma de identidad para seno en el Teorema 10.15 para mostrar que\(f(x) = a \, \sin(\omega x) + b\, \cos(\omega x) + B\) (con\(\omega > 0\)) se puede reescribir como\(f(x) = \sqrt{a^{2} + b^{2}}\sin(\omega x + \phi) + B\).
37. Con la ayuda de tus compañeros de clase, expresa los dominios de las funciones en los Ejemplos 10.5.4 y 10.5.5 usando notación de intervalo extendido. (Volveremos a revisar esto en la Sección 10.7.)

En los Ejercicios 38 - 43, verificar la identidad graficando los lados derecho e izquierdo en una calculadora.

38. \(\sin^{2}(x) + \cos^{2}(x) = 1\)
39. \(\sec^{2}(x) - \tan^{2}(x) = 1\)
40. \(\cos(x) = \sin\left(\dfrac{\pi}{2} - x\right)\)
41. \(\tan(x+\pi) = \tan(x)\)
42. \(\sin(2x) = 2\sin(x)\cos(x)\)
43. \(\tan\left(\dfrac{x}{2}\right) = \dfrac{\sin(x)}{1+\cos(x)}\)

En Ejercicios 44 - 50, grafica la función con la ayuda de tu calculadora y discute las preguntas dadas con tus compañeros de clase.

44. \(f(x) = \cos(3x) + \sin(x)\). ¿Esta función es periódica? Si es así, ¿cuál es el periodo?
45. \(f(x) = \frac{\sin(x)}{x}\). ¿Cuál parece ser la asíntota horizontal de la gráfica?
46. \(f(x) = x \sin(x)\). Gráfica\(y = \pm x\) sobre el mismo conjunto de ejes y describe el comportamiento de\(f\).
47. \(f(x) = \sin\left(\frac{1}{x}\right)\). ¿Qué está pasando como\(x \rightarrow 0\)?
48. \(f(x) = x - \tan(x)\). Gráfica\(y = x\) sobre el mismo conjunto de ejes y describe el comportamiento de\(f\).
49. \(f(x) = e^{-0.1x} \left( \cos(2x) + \sin(2x)\right)\). Gráfica\(y = \pm e^{-0.1x}\) sobre el mismo conjunto de ejes y describe el comportamiento de\(f\).
50. \(f(x) = e^{-0.1x} \left( \cos(2x) + 2\sin(x)\right)\). Gráfica\(y = \pm e^{-0.1x}\) sobre el mismo conjunto de ejes y describe el comportamiento de\(f\).
51. Demostrar que una función constante\(f\) es periódica mostrando eso\(f(x + 117) = f(x)\) para todos los números reales\(x\). Entonces demuestre que no\(f\) tiene periodo mostrando que no se puede encontrar un número más pequeño\(p\) tal que\(f(x + p) = f(x)\) para todos los números reales\(x\). Dicho de otra manera, mostrar que\(f(x + p) = f(x)\) para todos los números reales\(x\) para TODOS los valores de\(p > 0\), por lo que no existe ningún valor más pequeño para satisfacer la definición de 'período'.

10.5.5. RESPUESTAS

1. \(y = 3\sin(x)\)
   Período:\(2\pi\)
   Amplitud: Desplazamiento de\(3\)
   fase: Desplazamiento\(0\)
   vertical\(0\)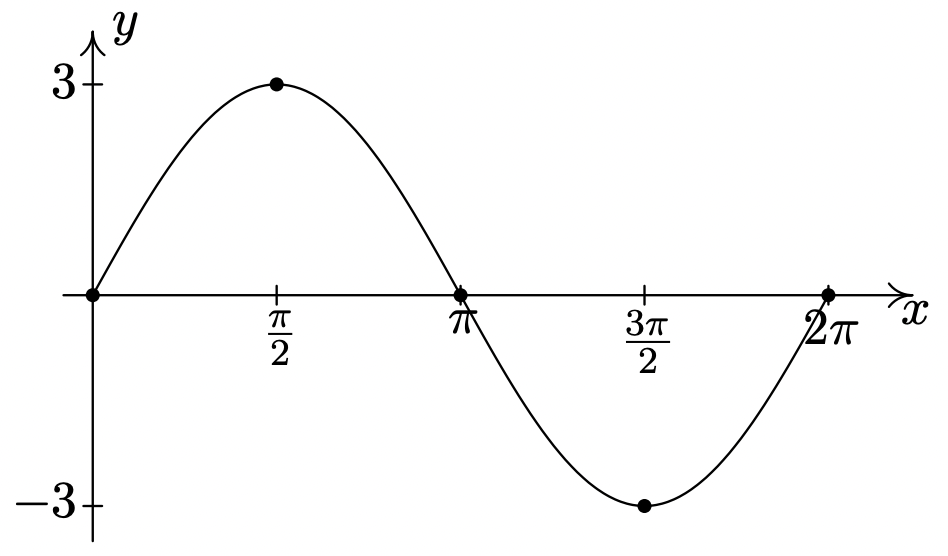

   

2. \(y = \sin(3x)\)
   Período:\(\dfrac{2\pi}{3}\)
   Amplitud: Desplazamiento de\(1\)
   fase: Desplazamiento\(0\)
   vertical\(0\)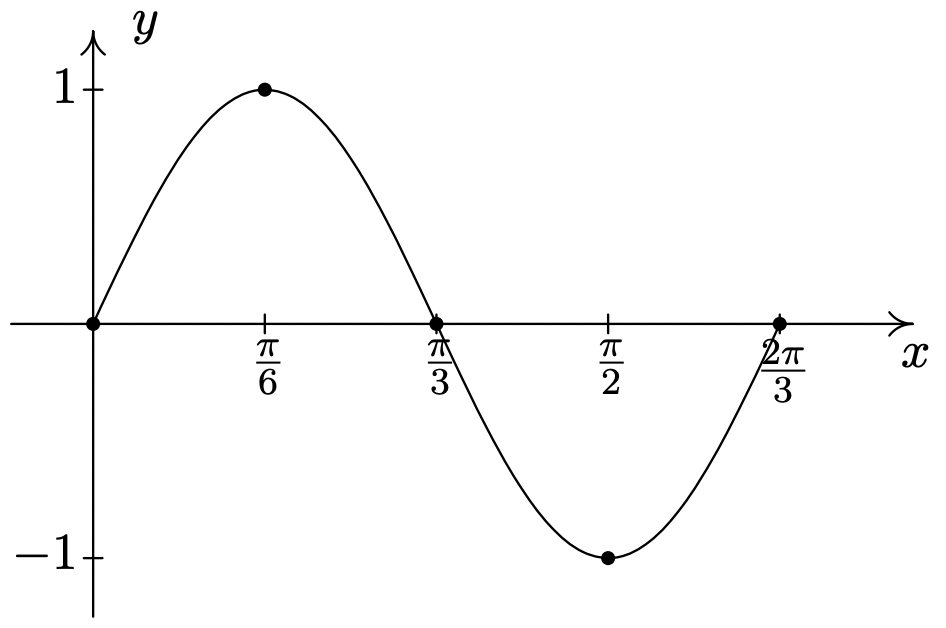

   

3. \(y = -2\cos(x)\)
   Período:\(2\pi\)
   Amplitud: Desplazamiento de\(2\)
   fase: Desplazamiento\(0\)
   vertical\(0\)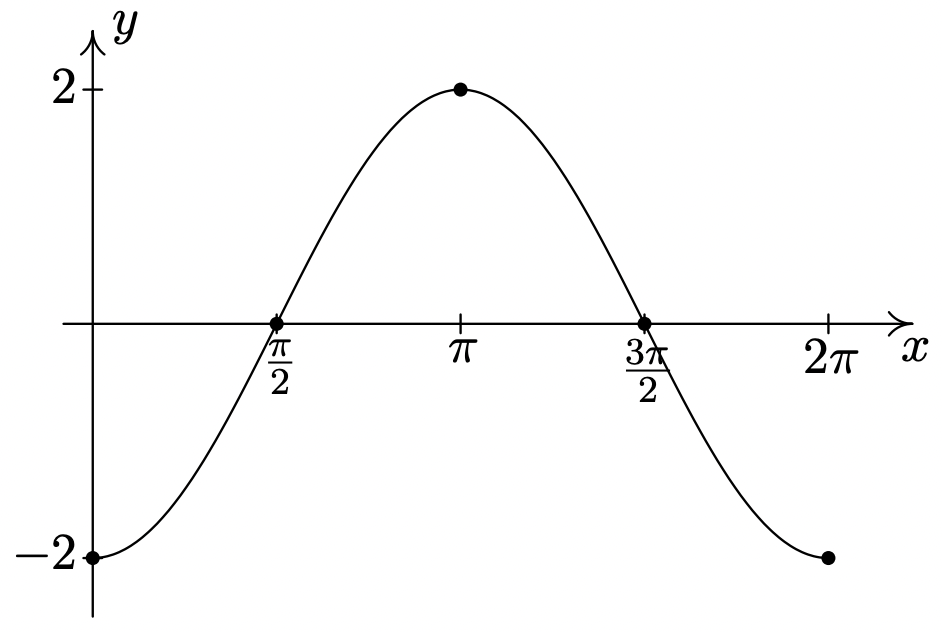

   

4. \(y = \cos \left( x - \dfrac{\pi}{2} \right)\)
   Período:\(2\pi\)
   Amplitud: Desplazamiento de\(1\)
   fase: Desplazamiento\(\dfrac{\pi}{2}\)
   vertical\(0\)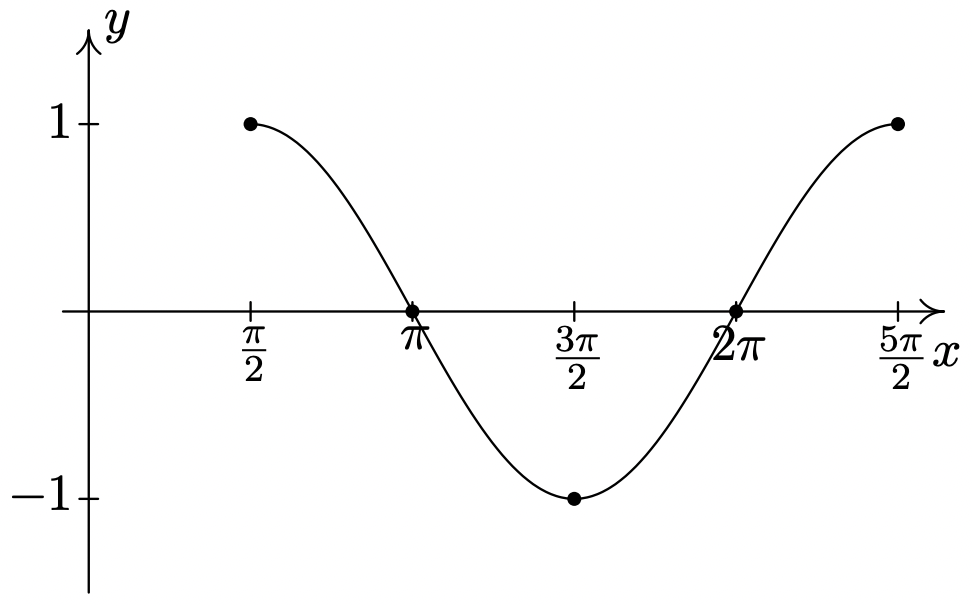

   

5. \(y = -\sin \left( x + \dfrac{\pi}{3} \right)\)
   Período:\(2\pi\)
   Amplitud: Desplazamiento de\(1\)
   fase: Desplazamiento\(-\dfrac{\pi}{3}\)
   vertical\(0\)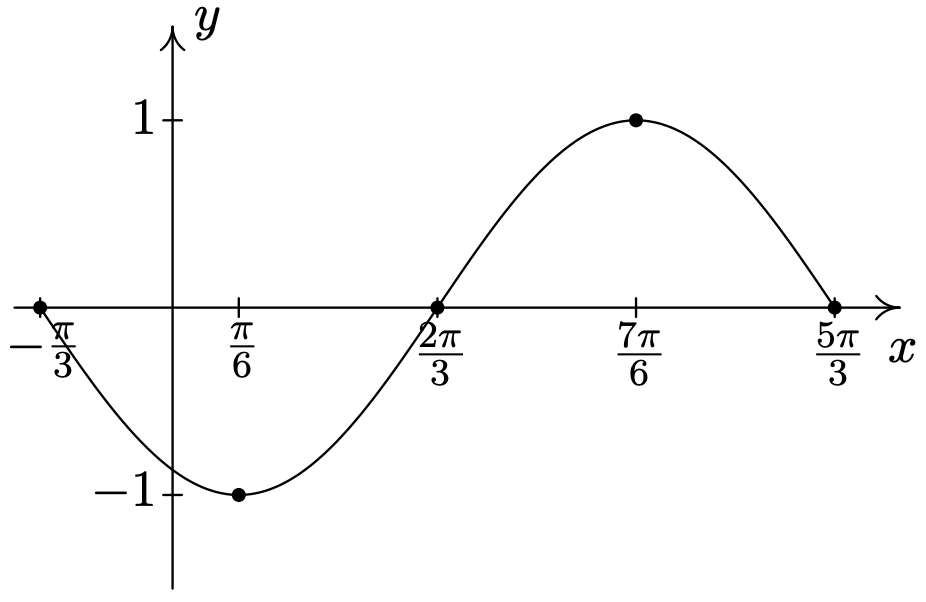

   

6. \(y = \sin(2x - \pi)\)
   Período:\(\pi\)
   Amplitud: Desplazamiento de\(1\)
   fase: Desplazamiento\(\dfrac{\pi}{2}\)
   vertical\(0\)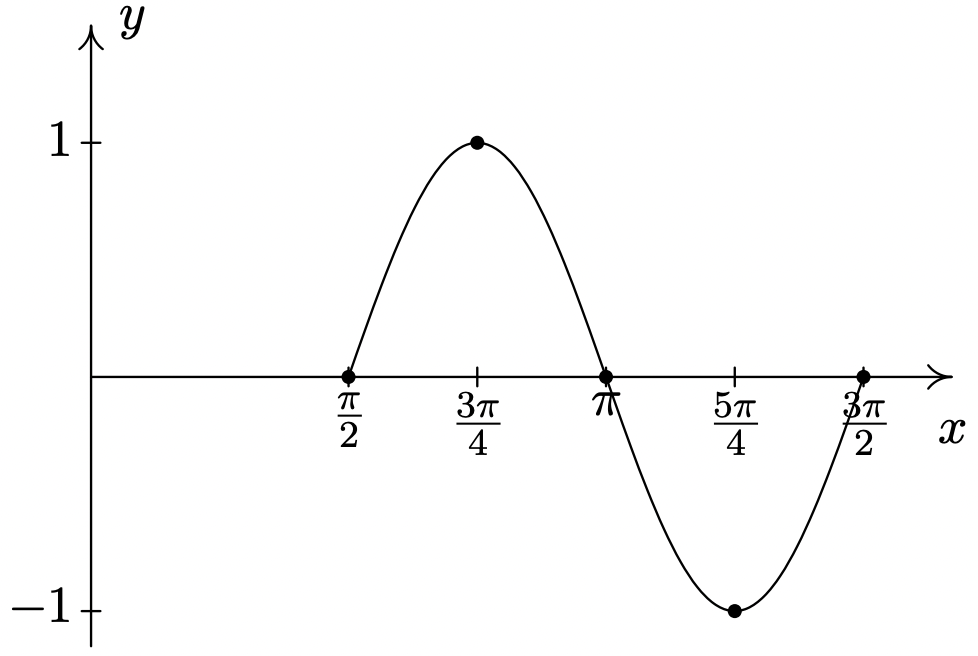

   

7. \(y = -\dfrac{1}{3}\cos \left( \dfrac{1}{2}x + \dfrac{\pi}{3} \right)\)
   Período:\(4\pi\)
   Amplitud: Desplazamiento de\(\dfrac{1}{3}\)
   fase: Desplazamiento\(-\dfrac{2\pi}{3}\)
   vertical\(0\)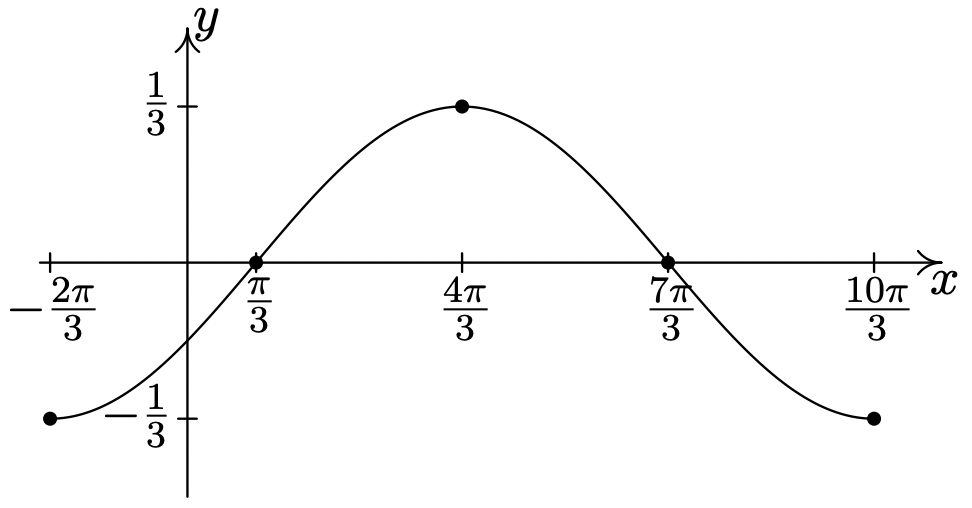

   

8. \(y = \cos (3x - 2\pi) + 4\)
   Período:\(\dfrac{2\pi}{3}\)
   Amplitud: Desplazamiento de\(1\)
   fase: Desplazamiento\(\dfrac{2\pi}{3}\)
   vertical: 4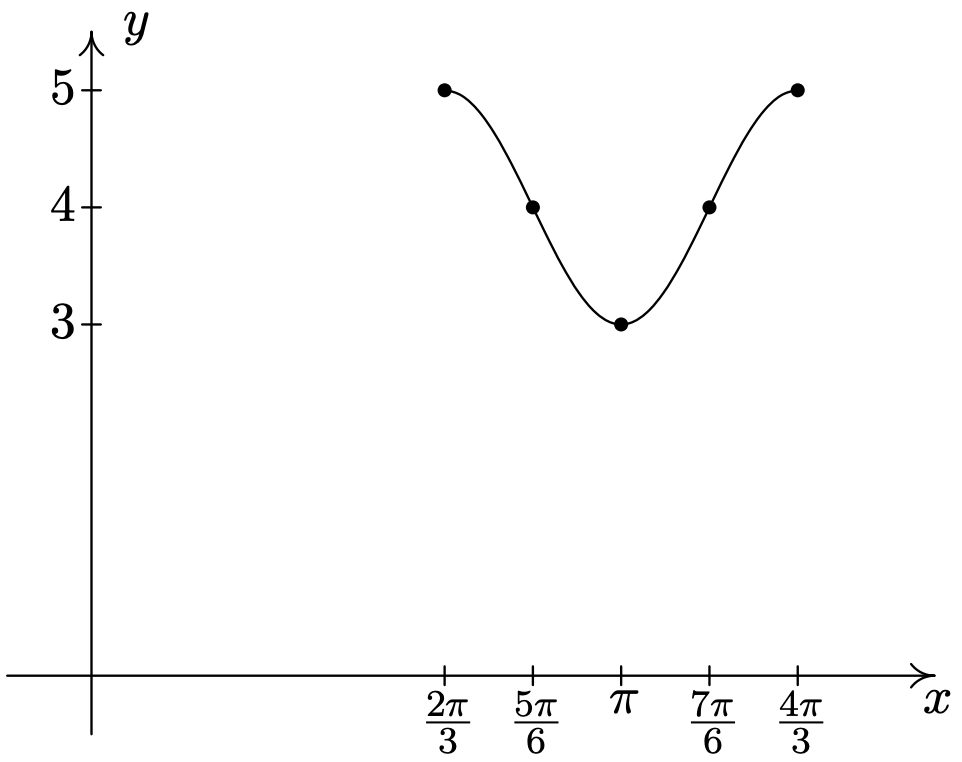

   

9. \(y = \sin \left( -x - \dfrac{\pi}{4} \right) - 2\)
   Periodo:\(2\pi\)
   Amplitud: Desplazamiento de\(1\)
   fase:\(-\dfrac{\pi}{4}\) (Es necesario utilizar
   \(y = -\sin \left( x + \dfrac{\pi}{4} \right) - 2\) para encontrar esto.) ¹⁵ Desplazamiento
   vertical:\(-2\)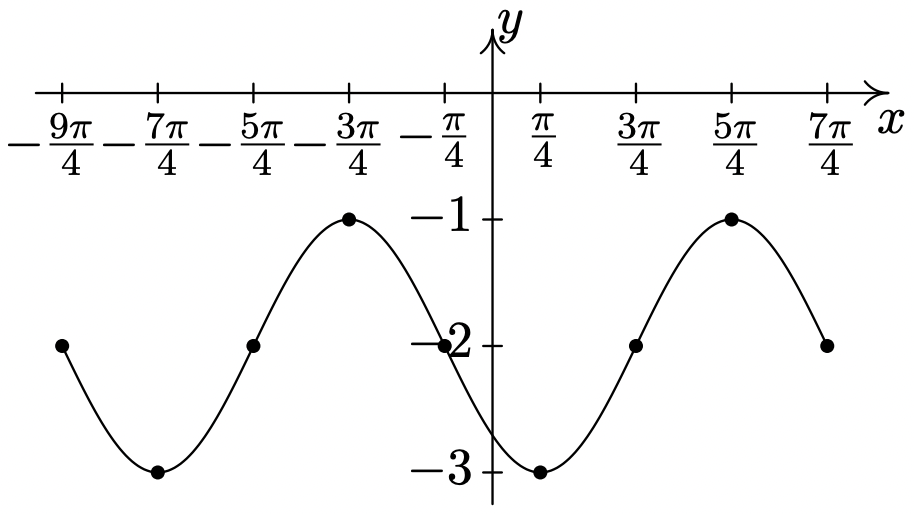

   

10. \(y = \dfrac{2}{3} \cos \left( \dfrac{\pi}{2} - 4x \right) + 1\)
    Periodo:\(\dfrac{\pi}{2}\)
    Amplitud: Desplazamiento de\(\dfrac{2}{3}\)
    fase:\(\dfrac{\pi}{8}\) (Es necesario utilizar
    \(y = \dfrac{2}{3} \cos \left( 4x - \dfrac{\pi}{2} \right) + 1\) para encontrar esto.) Desplazamiento
    vertical ¹⁶:\(1\)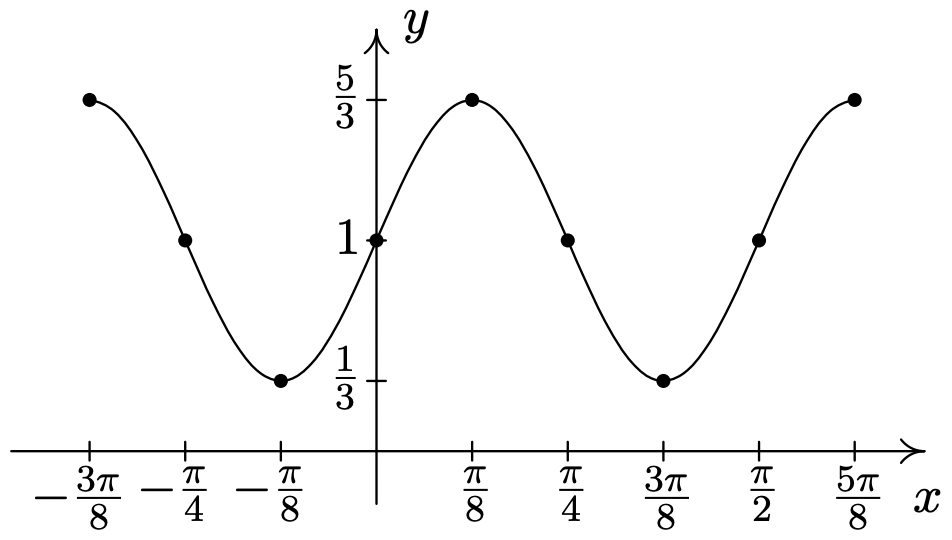

    

11. \(y = -\dfrac{3}{2} \cos \left( 2x + \dfrac{\pi}{3} \right) - \dfrac{1}{2}\)
    Período:\(\pi\)
    Amplitud: Desplazamiento de\(\dfrac{3}{2}\)
    fase: Desplazamiento\(-\dfrac{\pi}{6}\)
    vertical\(-\dfrac{1}{2}\)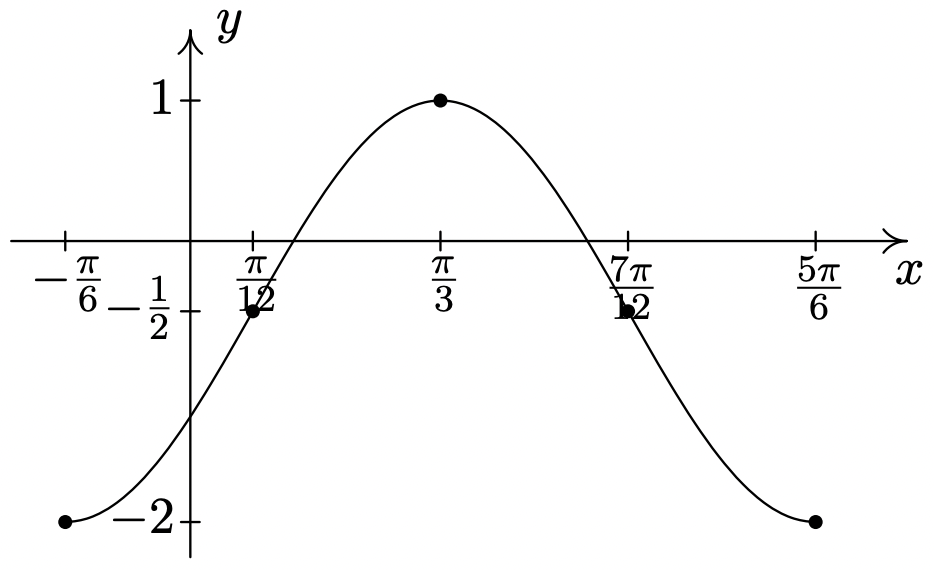

    

12. \(y = 4\sin (-2\pi x + \pi)\)
    Periodo:\(1\)
    Amplitud: Desplazamiento de\(4\)
    fase:\(\dfrac{1}{2}\) (Es necesario utilizar
    \(y = -4\sin (2\pi x - \pi)\) para encontrar esto.) Desplazamiento
    vertical ¹⁷:\(0\)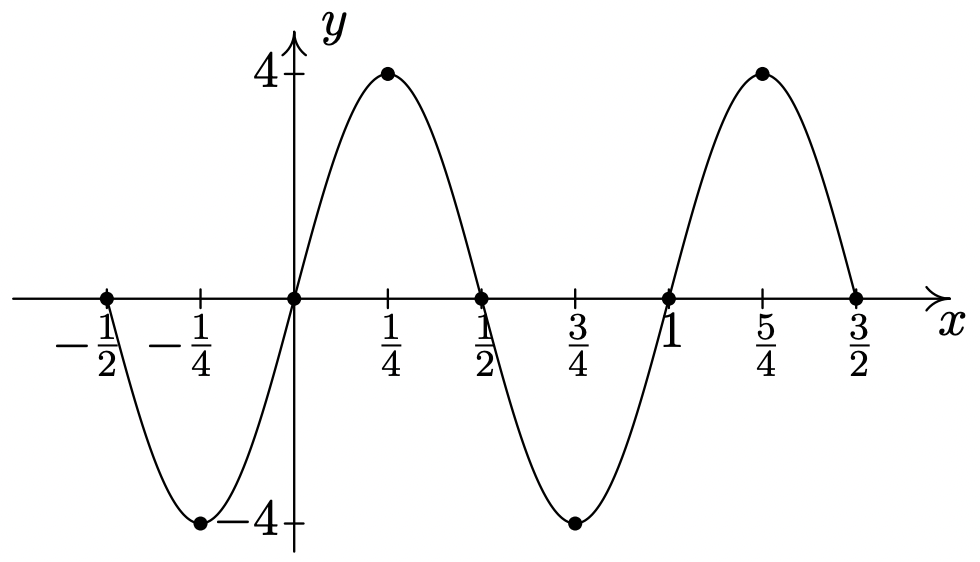

    

13. \(y = \tan \left(x - \dfrac{\pi}{3} \right)\)
    Periodo:\(\pi\)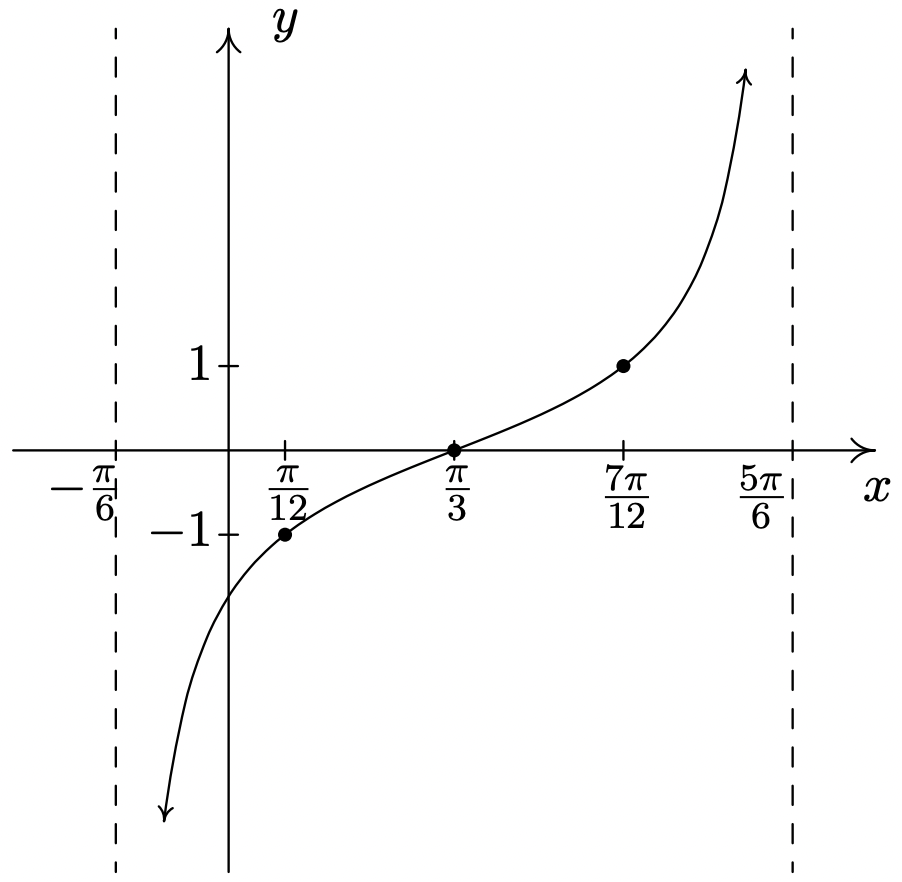

    

14. \(y = 2\tan \left( \dfrac{1}{4}x \right) - 3\)
    Periodo:\(4\pi\)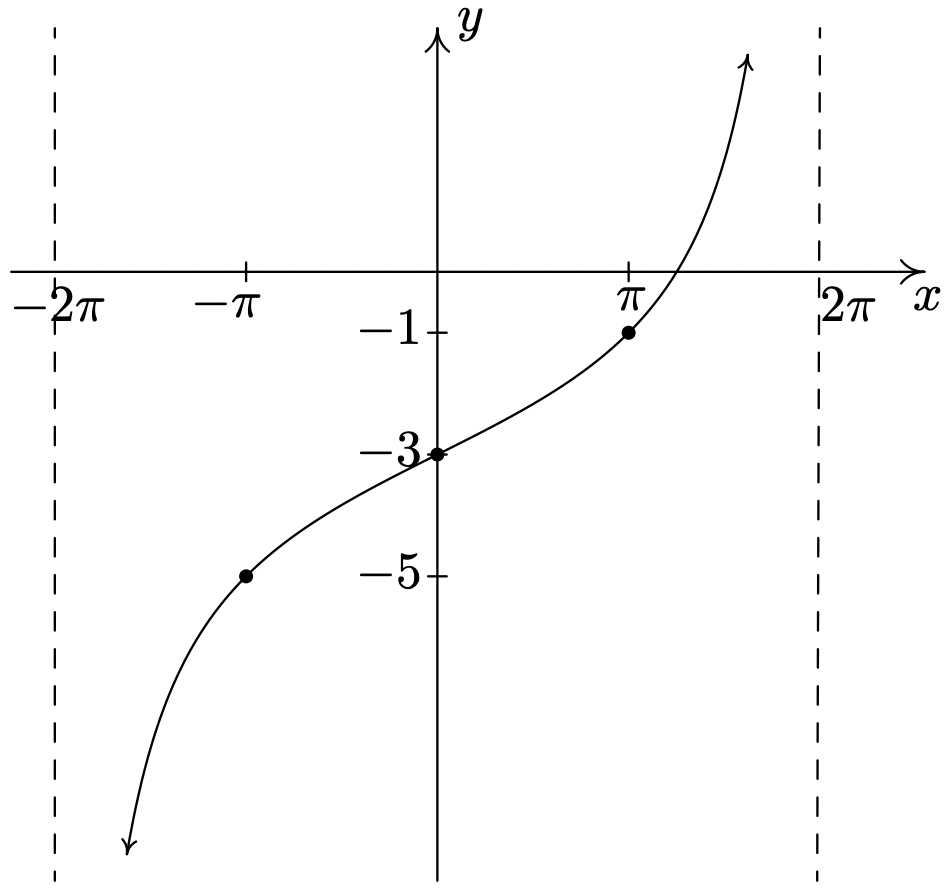

    

15. \(y = \dfrac{1}{3}\tan(-2x - \pi) + 1\)
    es equivalente a
    \(y = -\dfrac{1}{3}\tan(2x + \pi) + 1\)
    vía de la identidad par/impar para tangente.
    Periodo:\(\dfrac{\pi}{2}\)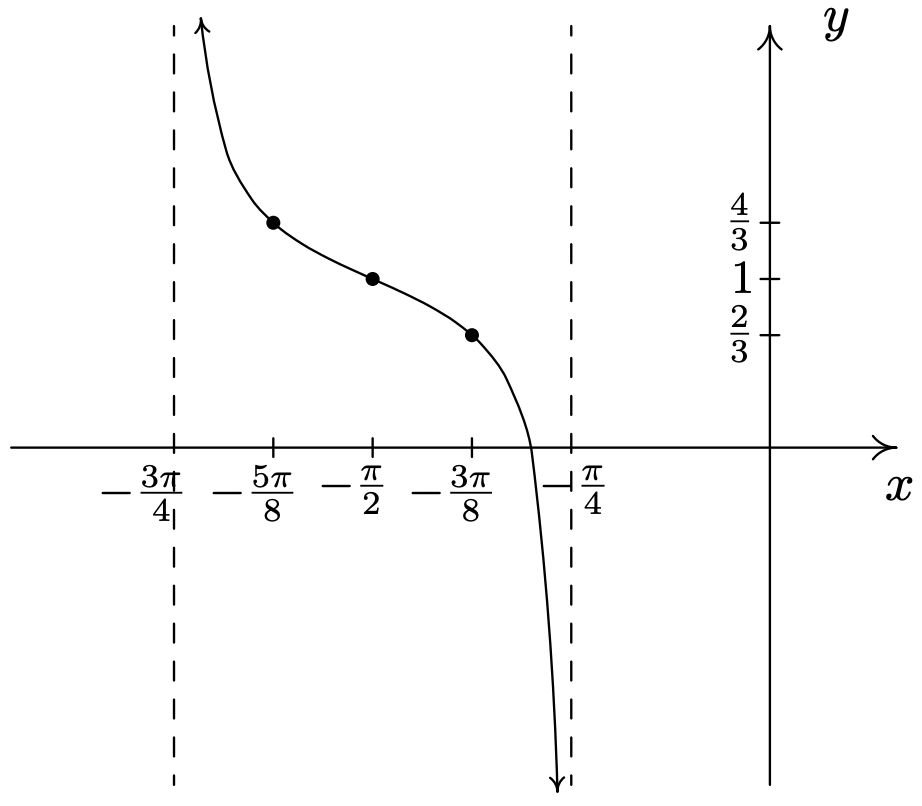

    

16. \(y = \sec \left( x - \frac{\pi}{2} \right)\)
    Comience con\(y = \cos \left( x - \frac{\pi}{2} \right)\)
    Periodo:\(2\pi\)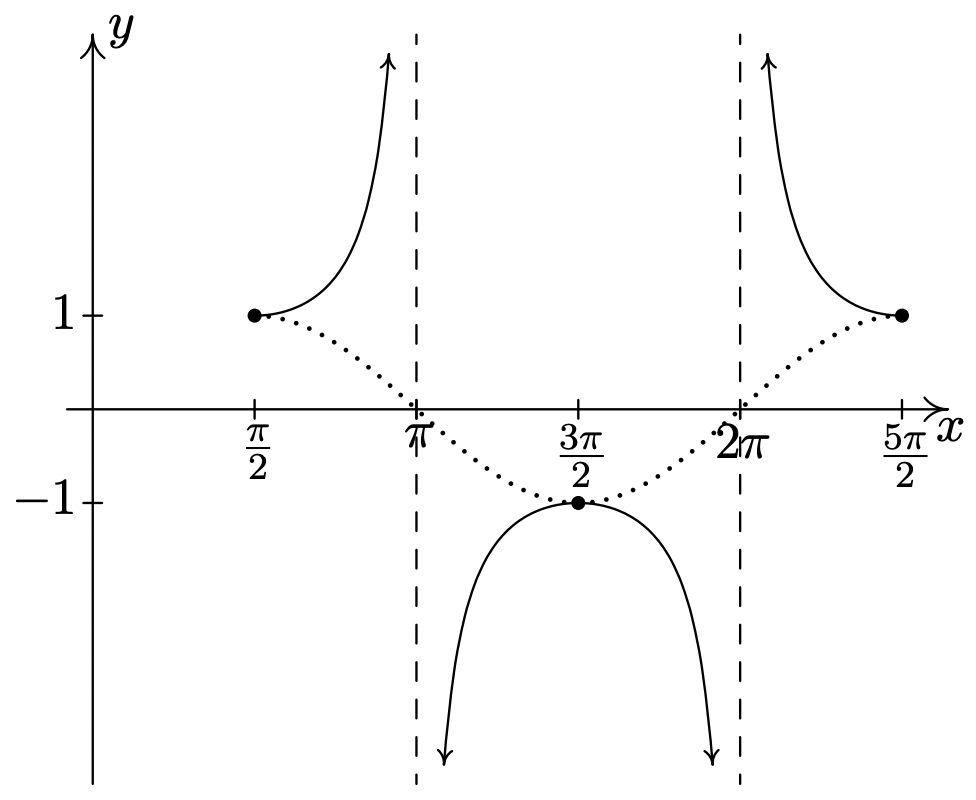

    

17. \(y = -\csc \left( x + \dfrac{\pi}{3} \right)\)
    Comience con\(y = -\sin \left( x + \dfrac{\pi}{3} \right)\)
    Periodo:\(2\pi\)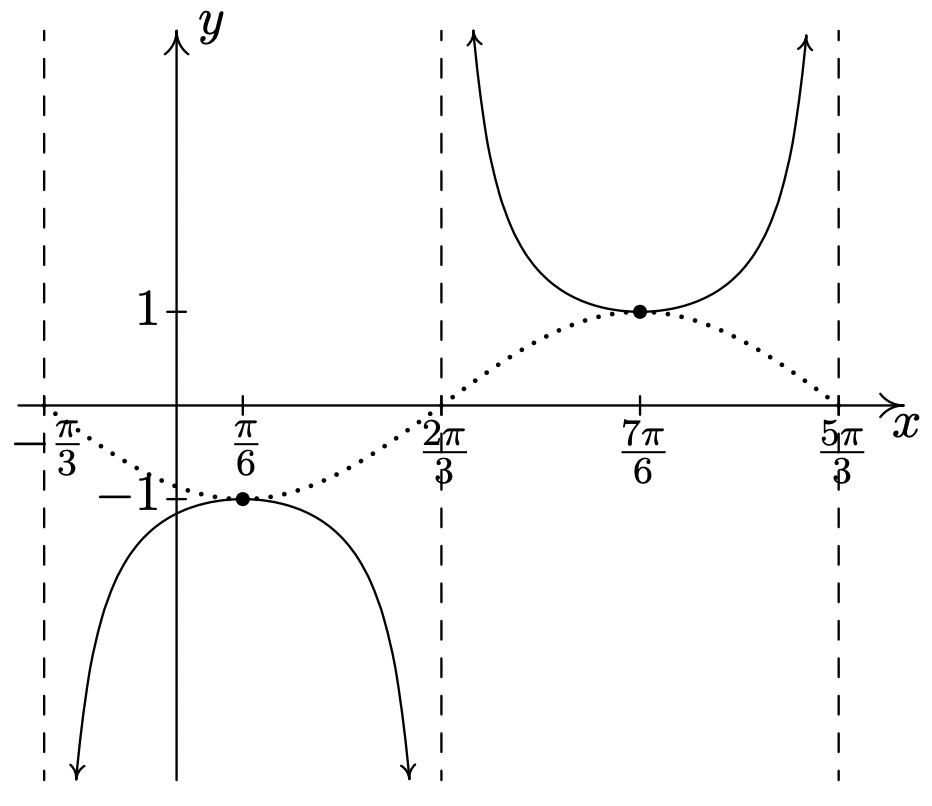

    

18. \(y = -\dfrac{1}{3} \sec \left( \dfrac{1}{2}x + \dfrac{\pi}{3} \right)\)
    Comience con\(y = -\dfrac{1}{3}\cos \left( \dfrac{1}{2}x + \dfrac{\pi}{3} \right)\)
    Periodo:\(4\pi\)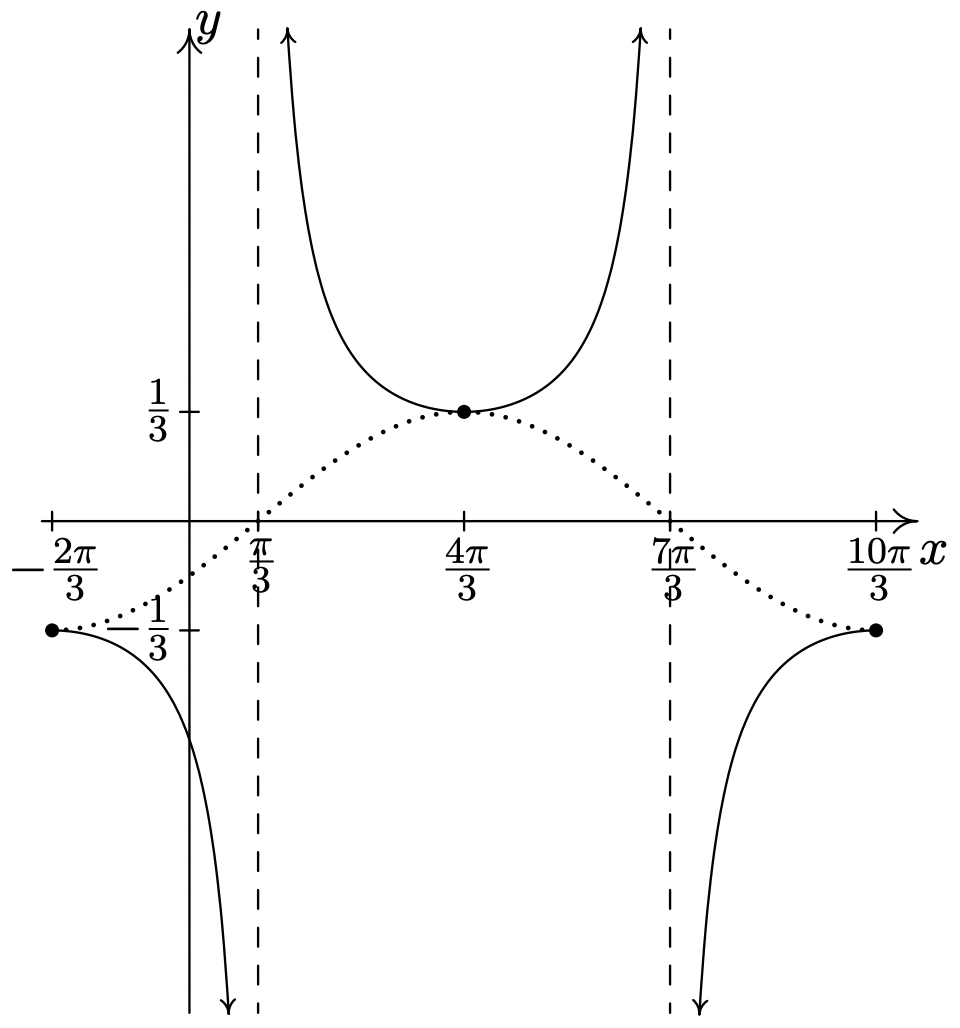

    

19. \(y = \csc (2x - \pi)\)
    Comience con\(y = \sin(2x - \pi)\)
    Periodo:\(\pi\)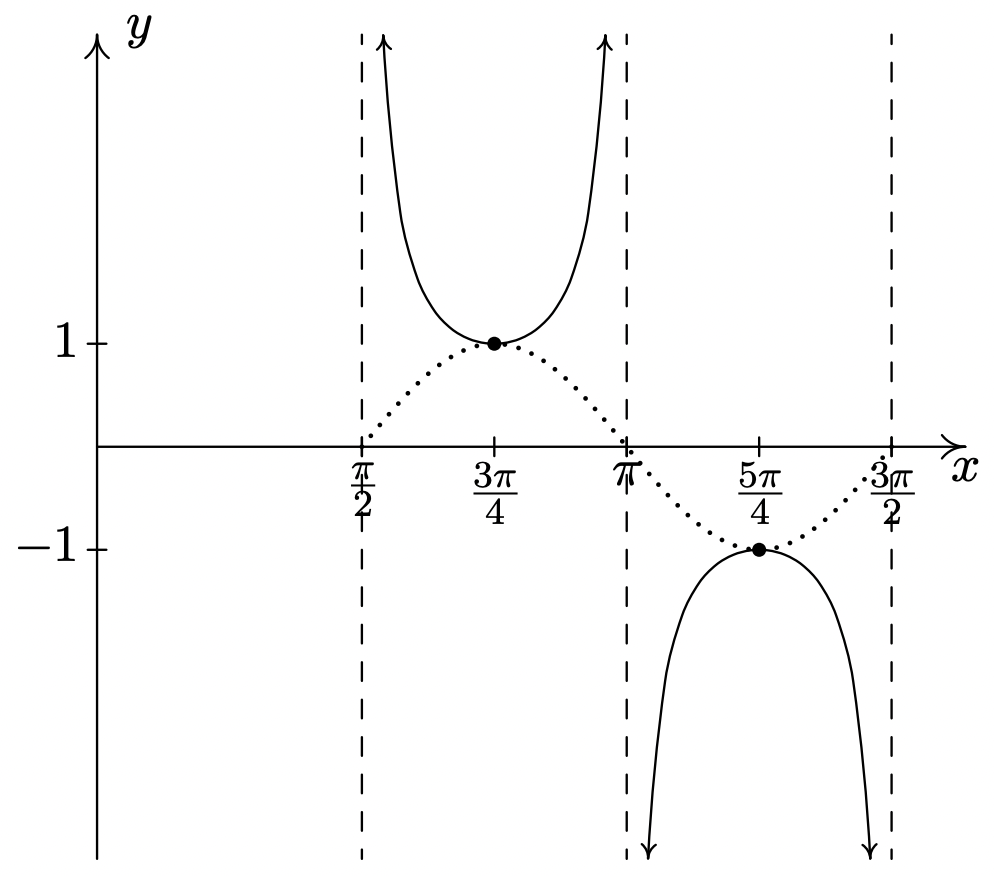

    

20. \(y = \sec(3x - 2\pi) + 4\)
    Comience con\(y = \cos (3x - 2\pi) + 4\)
    Periodo:\(\dfrac{2\pi}{3}\)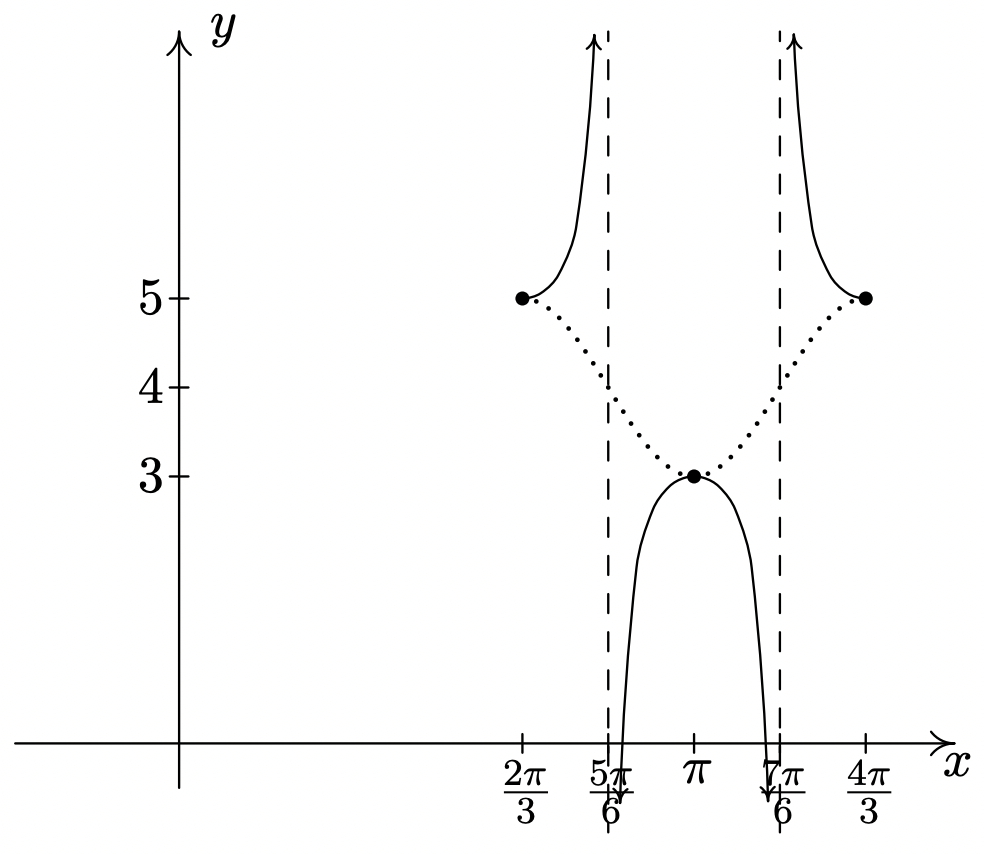

    

21. \(y = \csc \left( -x - \dfrac{\pi}{4} \right) - 2\)
    Comience con\(y = \sin \left( -x - \dfrac{\pi}{4} \right) - 2\)
    Periodo:\(2\pi\)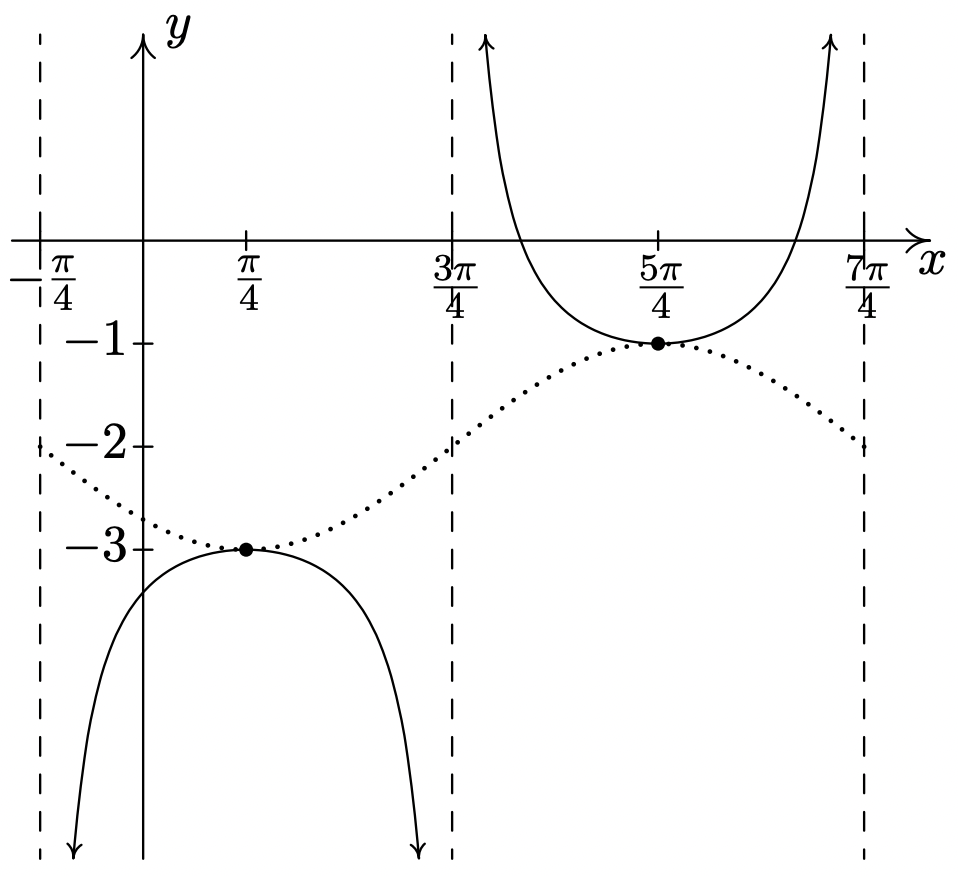

    

22. \(y = \cot \left( x + \dfrac{\pi}{6} \right)\)
    Periodo:\(\pi\)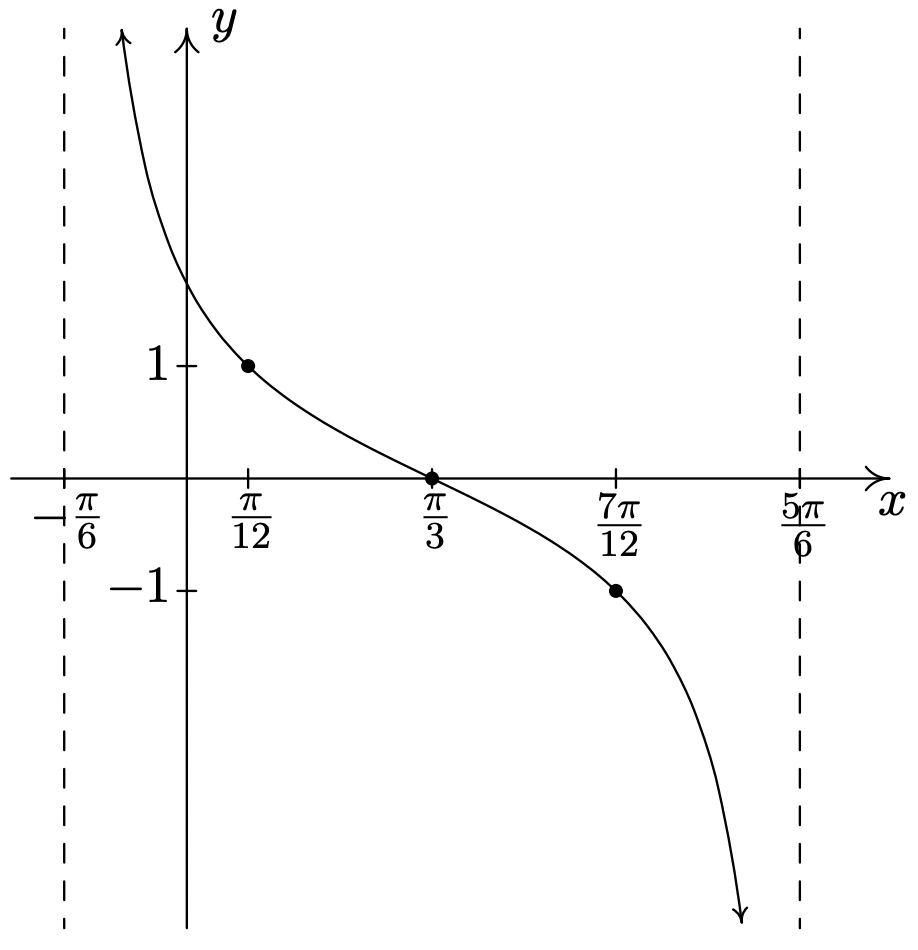

    

23. \(y = -11\cot \left( \dfrac{1}{5} x \right)\)
    Periodo:\(5\pi\)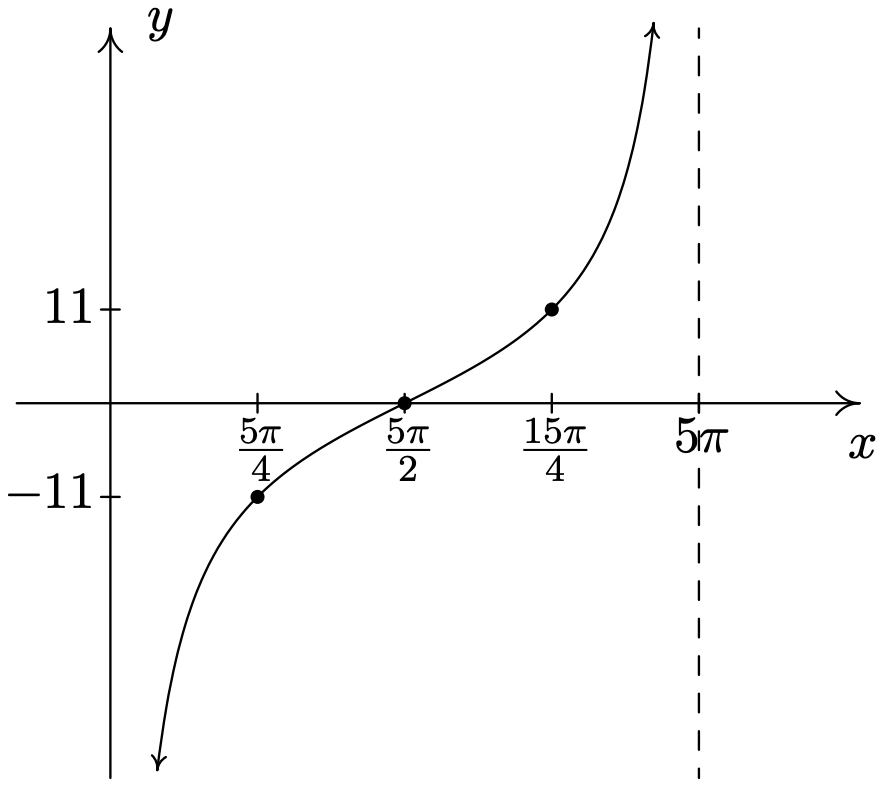

    

24. \(y = \dfrac{1}{3} \cot \left( 2x + \dfrac{3\pi}{2} \right) + 1\)
    Periodo:\(\dfrac{\pi}{2}\)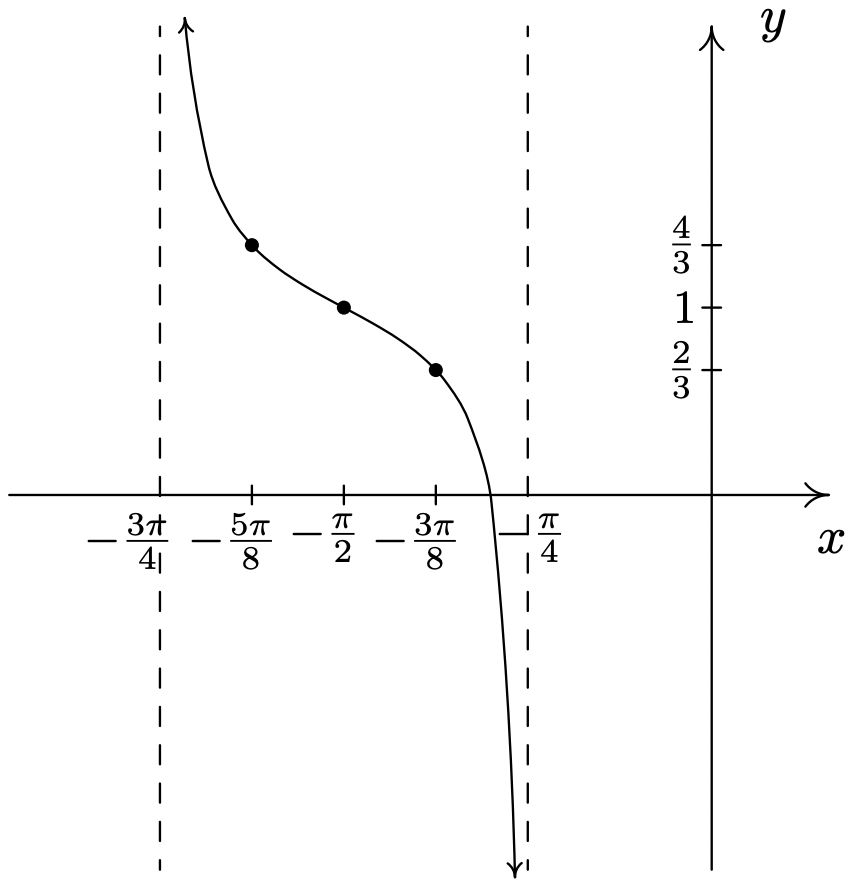

    

25. \(f(x) = \sqrt{2}\sin(x) + \sqrt{2}\cos(x) + 1 = 2\sin\left(x + \dfrac{\pi}{4}\right) + 1 = 2\cos\left(x + \dfrac{7\pi}{4}\right) + 1\)
26. \(f(x) = 3\sqrt{3}\sin(3x) - 3\cos(3x) = 6\sin\left(3x + \dfrac{11\pi}{6}\right) = 6\cos\left(3x + \dfrac{4\pi}{3}\right)\)
27. \(f(x) = -\sin(x) + \cos(x) - 2 = \sqrt{2}\sin\left(x + \dfrac{3\pi}{4}\right) - 2 = \sqrt{2}\cos\left(x + \dfrac{\pi}{4}\right) - 2\)
28. \(f(x) = -\dfrac{1}{2}\sin(2x) - \dfrac{\sqrt{3}}{2}\cos(2x) = \sin\left(2x + \dfrac{4\pi}{3}\right) = \cos\left(2x + \dfrac{5\pi}{6}\right)\)
29. \(f(x) = 2\sqrt{3} \cos(x) - 2\sin(x) = 4\sin\left(x+\dfrac{2\pi}{3} \right) = 4\cos\left(x + \dfrac{\pi}{6}\right)\)
30. \(f(x) = \dfrac{3}{2} \cos(2x) - \dfrac{3\sqrt{3}}{2} \sin(2x) + 6 =3\sin\left(2x + \dfrac{5\pi}{6}\right) + 6 = 3\cos\left(2x + \dfrac{\pi}{3}\right) + 6\)
31. \(f(x) = -\dfrac{1}{2} \cos(5x) -\dfrac{\sqrt{3}}{2} \sin(5x) = \sin\left(5x + \dfrac{7\pi}{6}\right) = \cos\left(5x + \dfrac{2\pi}{3}\right)\)
32. \(f(x) = -6\sqrt{3} \cos(3x) - 6\sin(3x) - 3 = 12\sin\left(3x + \dfrac{4\pi}{3}\right) - 3 = 12\cos\left(3x + \dfrac{5\pi}{6}\right) - 3\)
33. \(f(x) = \dfrac{5\sqrt{2}}{2} \sin(x) -\dfrac{5\sqrt{2}}{2} \cos(x) = 5\sin\left(x + \dfrac{7\pi}{4}\right)= 5\cos\left(x + \dfrac{5\pi}{4}\right)\)
34. \(f(x) =3\sin\left(\dfrac{x}{6}\right) -3\sqrt{3} \cos\left(\dfrac{x}{6}\right) = 6\sin\left( \dfrac{x}{6}+\dfrac{5\pi}{3}\right)= 6\cos\left( \dfrac{x}{6}+\dfrac{7\pi}{6}\right)\)

---

Referencia

¹ Véase la sección 1.6 para una revisión de estos conceptos.

² Alternativamente, podemos usar las Identidades de Cofunción en el Teorema 10.14 para mostrar que\(g(t)=\sin (t)\) es periódico con periodo\(2 \pi\) desde\(g(t)=\sin (t)=\cos \left(\frac{\pi}{2}-t\right)=f\left(\frac{\pi}{2}-t\right)\).

³ Técnicamente, debemos estudiar el intervalo\([0,2 \pi)\), ⁴ ya que lo que pase en\(t=2 \pi\) es lo mismo que lo que sucede en\(t = 0\). Como veremos en breve, nos\(t=2 \pi\) da un 'check' extra cuando vayamos a graficar estas funciones.

⁴ En algunos textos avanzados, el intervalo de elección es\([-\pi, \pi)\).

⁵ El uso\(x\) y\(y\) en este contexto no debe confundirse con las\(y\) coordenadas\(x\) - y -de los puntos del Círculo Unitario que definen coseno y seno. Usar el término 'función trigonométrica' en lugar de 'función circular' puede ayudar con eso, pero uno podría entonces preguntar: “Oye, ¿dónde está el triángulo

⁶ Ya hemos visto cómo se pueden utilizar las Identidades Par/Impares y Cofunción para reescribir\(g(x)=\sin (x)\) como una versión transformada de\(f(x)=\cos (x)\), así que por supuesto, lo contrario es cierto: se\(f(x)=\cos (x)\) puede escribir como una versión transformada de\(g(x)=\sin (x)\). Los autores han visto algunos casos en los que las sinusoides siempre se convierten en funciones coseno mientras que en otras disciplinas, las sinusoides siempre se escriben en términos de funciones sinusoidales. Discutiremos las aplicaciones de los sinusoides con mayor detalle en el Capítulo 11. Hasta entonces, mantendremos nuestras opciones

⁷ Intente usar las fórmulas en el Teorema 10.23 aplicadas\(C(x)=\cos (-x+\pi)\) para ver por qué necesitamos\(\omega>0\).

⁸ Esto debería recordarle los coeficientes de ecuación de potencias similares de\(x\) la Sección 8.6.

⁹ ¡Ten cuidado aquí!

¹⁰ ¡Esta gráfica, sin embargo, exhibe características similares a sinusoides! ¡Compruébalo!

¹¹ Se proporcionan\(\sec (\alpha)\) y\(\sec (\beta)\) se definen,\(\sec (\alpha)=\sec (\beta)\) si y solo si\(\cos (\alpha)=\cos (\beta)\). De ahí,\(\sec (x)\) hereda su periodo de\(\cos (x)\).

¹² En la Sección 10.3.1, argumentamos el rango de\(F(x)=\sec (x)\) is\((-\infty,-1] \cup[1, \infty)\). Ahora podemos ver esto gráficamente.

¹³ Al igual que las funciones racionales del Capítulo 4 son continuas y suaves en sus dominios porque los polinomios son continuos y suaves en todas partes, las funciones secante y cosecante son continuas y suaves en sus dominios ya que las funciones coseno y seno son continuas y suave en todas partes.

¹⁴ Ciertamente, imitando la prueba de que el periodo de\(\tan (x)\) es una opción; para otro enfoque, considerar transformar\(\tan (x)\) a\(\cot (x)\) usar identidades.

¹⁵ Se muestran dos ciclos de la gráfica para ilustrar la discrepancia discutida en la página 796.

¹⁶ Nuevamente, graficamos dos ciclos para ilustrar la discrepancia discutida en la página 796.

¹⁷ Esta será la última vez que graficemos dos ciclos para ilustrar la discrepancia discutida en la página 796.