11.10: Ecuaciones paramétricas

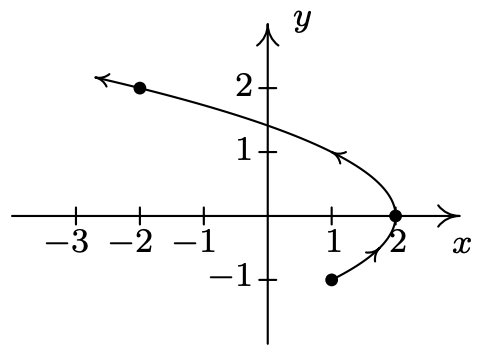
Como hemos visto en los Ejercicios 53 - 56 de la Sección 1.2, Capítulo 7 y más recientemente en la Sección 11.5, hay puntuaciones de curvas interesantes que, cuando se trazan en el\(xy\) plano, no representan\(y\) en función de\(x\) ni\(x\) en función de\(y\). En esta sección, presentamos un nuevo concepto que nos permite utilizar funciones para estudiar este tipo de curvas. Para motivar la idea, imaginamos un error arrastrándose por la parte superior de una mesa comenzando en el punto\(O\) y trazando una curva\(C\) en el plano, como se muestra a continuación.

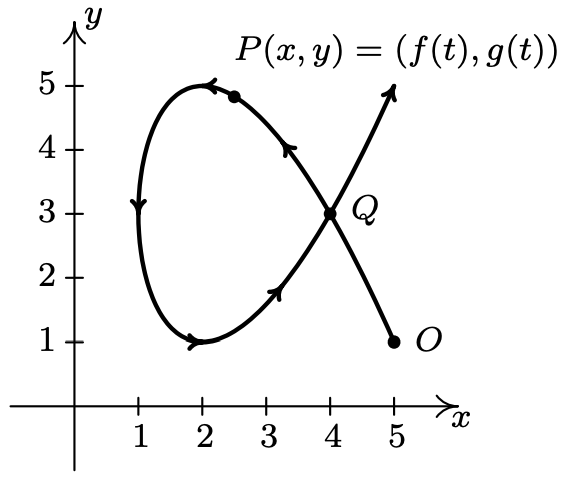
La curva\(C\) no representa\(y\) en función de\(x\) porque falla la Prueba de Línea Vertical y no representa\(x\) en función de\(y\) porque falla la Prueba de Línea Horizontal. Sin embargo, dado que el error puede estar en un solo lugar\(P(x, y)\) en un momento dado\(t\), podemos definir la\(x\) -coordenada de\(P\) como una función de\(t\) y la\(y\) -coordenada de\(P\) como una función (generalmente, pero no necesariamente) diferente de\(t\). (Tradicionalmente,\(f(t)\) se utiliza para\(x\) y\(g(t)\) se utiliza para\(y\).) La variable independiente\(t\) en este caso se denomina parámetro y el sistema de ecuaciones\[\left\{\begin{array}{l} x=f(t) \\ y=g(t) \end{array}\right.\nonumber\] se denomina sistema de ecuaciones paramétricas o parametrización de la curva\(C\). ¹ La parametrización de la\(C\) dota de una orientación y las flechas sobre\(C\) indican movimiento en la dirección de valores crecientes de\(t\). En este caso, nuestro error comienza en el punto\(O\), viaja hacia arriba hacia la izquierda, luego recorre para cruzar su camino ² en el punto\(Q\) y finalmente se dirige hacia el primer cuadrante. Es importante señalar que la propia curva es un conjunto de puntos y como tal está desprovista de cualquier orientación. La parametrización determina la orientación y como veremos, diferentes parametrizaciones pueden determinar diferentes orientaciones. Si todo esto le parece embrujosamente familiar, debería. Por definición, el sistema de ecuaciones\(\{x=\cos (t), y=\sin (t)\) parametriza el Círculo de Unidad, dándole una orientación en sentido antihorario. De manera más general, las ecuaciones de movimiento circular\(\{x=r \cos (\omega t), y=r \sin (\omega t)\) desarrolladas en la página 732 de la Sección 10.2.1 son ecuaciones paramétricas que trazan un círculo de radio\(r\) centrado en el origen. Si\(\omega>0\), la orientación es en sentido antihorario; si\(\omega<0\), la orientación es en sentido horario. La frecuencia angular\(\omega\) determina 'qué tan rápido' el objeto se mueve alrededor del círculo. En particular, las ecuaciones\(\left\{x=2960 \cos \left(\frac{\pi}{12} t\right), y=2960 \sin \left(\frac{\pi}{12} t\right)\right.\) que modelan el movimiento de Lakeland Community College a medida que gira la tierra (ver Ejemplo 10.2.7 en la Sección 10.2) parametrizan un círculo de radio 2960 con una rotación en sentido antihorario que completa una revolución a medida que\(t\) recorre el intervalo [0, 24). Es hora de otro ejemplo

Ejemplo 11.10.1

Esbozar la curva descrita por\(\left\{\begin{array}{l} x=t^{2}-3 \\ y=2 t-1 \end{array} \text { for } t \geq-2\right..\)

Solución

Seguimos el mismo procedimiento aquí que tenemos una y otra vez cuando se nos pide graficar cualquier cosa nueva — elegir valores amigables de\(t\), trazar los puntos correspondientes y conectar los resultados de una manera agradable. Ya que nos dicen\(t \geq-2\), empezamos ahí y a medida que trazamos puntos sucesivos, dibujamos una flecha para indicar la dirección del camino para aumentar los valores de\(t\).

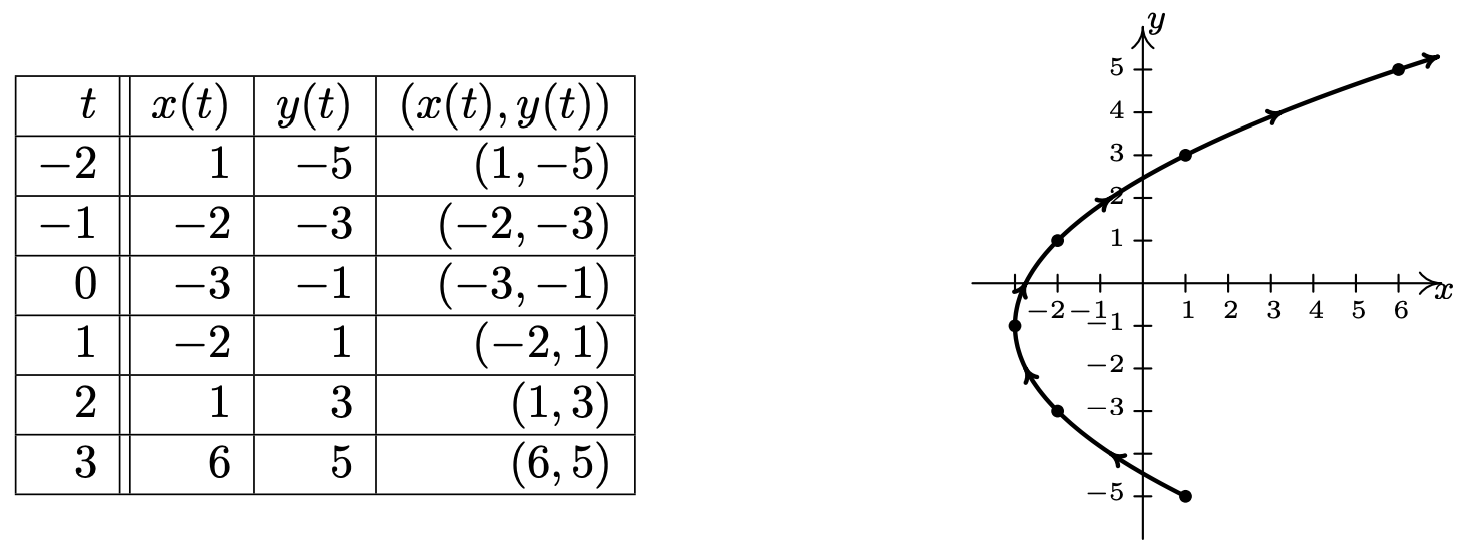
La curva esbozada en el Ejemplo 11.10.1 ciertamente parece una parábola, y la presencia del\(t^{2}\) término en la ecuación\(x=t^{2}-3\) refuerza esta corazonada. Dado que las ecuaciones paramétricas\(\left\{x=t^{2}-3, y=2 t-1\right.\) dadas para describir esta curva son un sistema de ecuaciones, podemos utilizar la técnica de sustitución como se describe en la Sección 8.7 para eliminar el parámetro\(t\) y obtener una ecuación que involucre justo\(x\) y\(y\). Para ello, elegimos resolver la ecuación\(y=2 t-1\)\(t\) para obtener\(t=\frac{y+1}{2}\). Sustituir esto en la ecuación\(x=t^{2}-3\) rinde\(x=\left(\frac{y+1}{2}\right)^{2}-3\) o, después de algún reordenamiento,\((y+1)^{2}=4(x+3)\). Pensando en la Sección 7.3, vemos que la gráfica de esta ecuación es una parábola con vértice\((−3, −1)\) que se abre a la derecha, según se requiera. Técnicamente hablando, la ecuación\((y+1)^{2}=4(x+3)\) describe toda la parábola, mientras que las ecuaciones paramétricas\(\left\{x=t^{2}-3, y=2 t-1 \text { for } t \geq-2\right.\) describen solo una porción de la parábola. En este caso, ³ podemos remediar esta situación restringiendo los límites en\(y\). Dado que la porción de la parábola que queremos es exactamente la parte donde\(y \geq-5\), la ecuación\((y+1)^{2}=4(x+3)\) acoplada con la restricción\(y \geq-5\) describe la misma curva que las ecuaciones paramétricas dadas. La única información que nunca podremos recuperar después de eliminar el parámetro es la orientación de la curva.

Eliminar el parámetro y obtener una ecuación en términos\(x\) y\(y\), siempre que sea posible, puede ser de gran ayuda para graficar curvas determinadas por ecuaciones paramétricas. Si el sistema de ecuaciones paramétricas contiene funciones algebraicas, como fue el caso en el Ejemplo 11.10.1, entonces se pueden aplicar al sistema las técnicas habituales de sustitución y eliminación aprendidas en la Sección 8.7\(\{x=f(t), y=g(t)\) para eliminar el parámetro. Si, por otro lado, la parametrización involucra las funciones trigonométricas, la estrategia cambia ligeramente. En este caso, a menudo es mejor resolver las funciones trigonométricas y relacionarlas usando una identidad. Demostramos estas técnicas en el siguiente ejemplo.

Ejemplo 11.10.2

Esboce las curvas descritas por las siguientes ecuaciones paramétricas.

1. \(\left\{\begin{array}{l} x=t^{3} \\ y=2 t^{2} \end{array} \quad \text { for }-1 \leq t \leq 1\right.\)
2. \(\left\{\begin{array}{l} x=e^{-t} \\ y=e^{-2 t} \quad \text { for } t \geq 0 \end{array}\right.\)
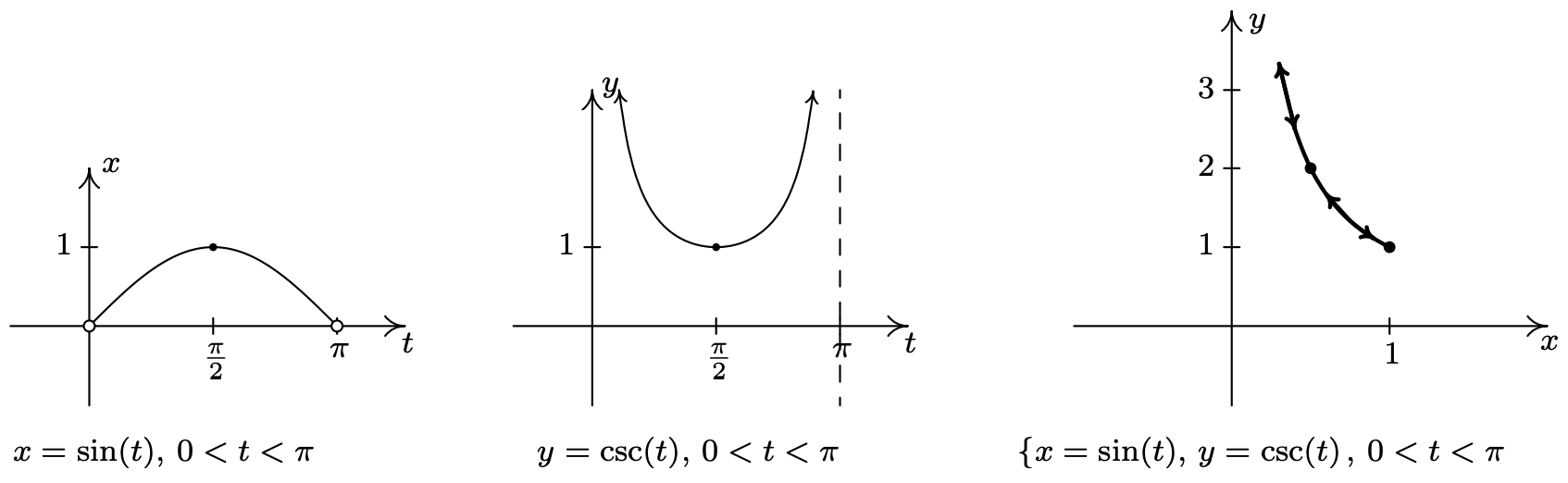
3. \(\left\{\begin{array}{l} x=\sin (t) \\ y=\csc (t) \end{array} \quad \text { for } 0<t<\pi\right.\)
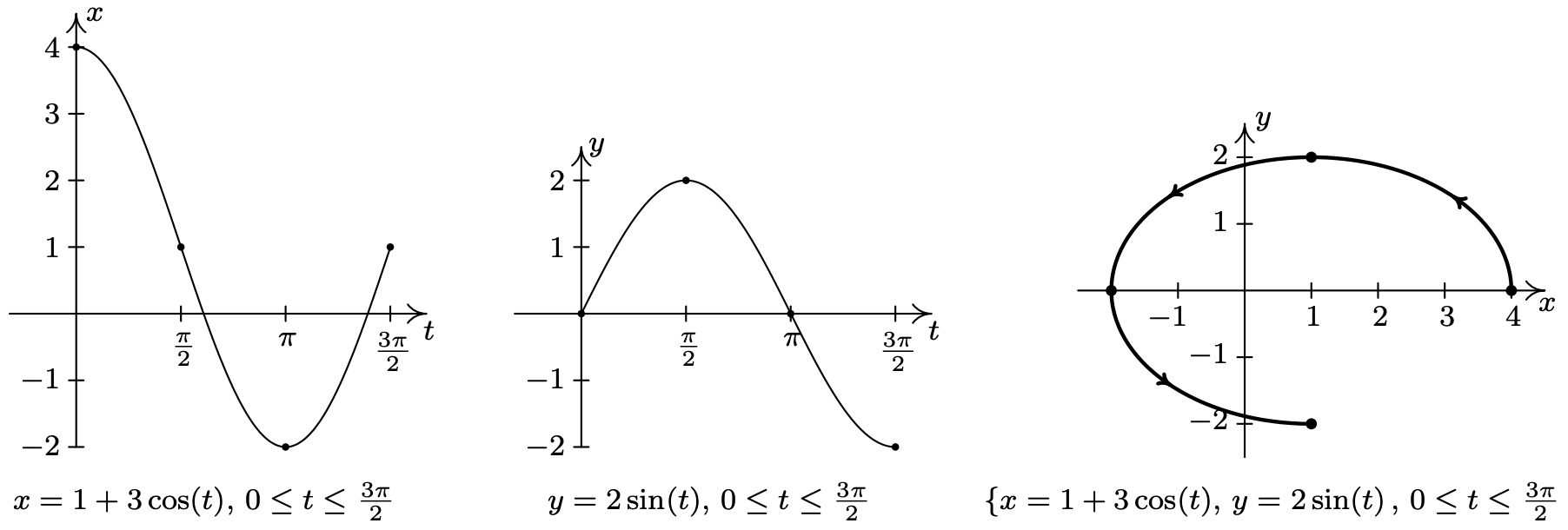
4. \(\left\{\begin{array}{l} x=1+3 \cos (t) \\ y=2 \sin (t) \end{array} \quad \text { for } 0 \leq t \leq \frac{3 \pi}{2}\right.\)

Solución

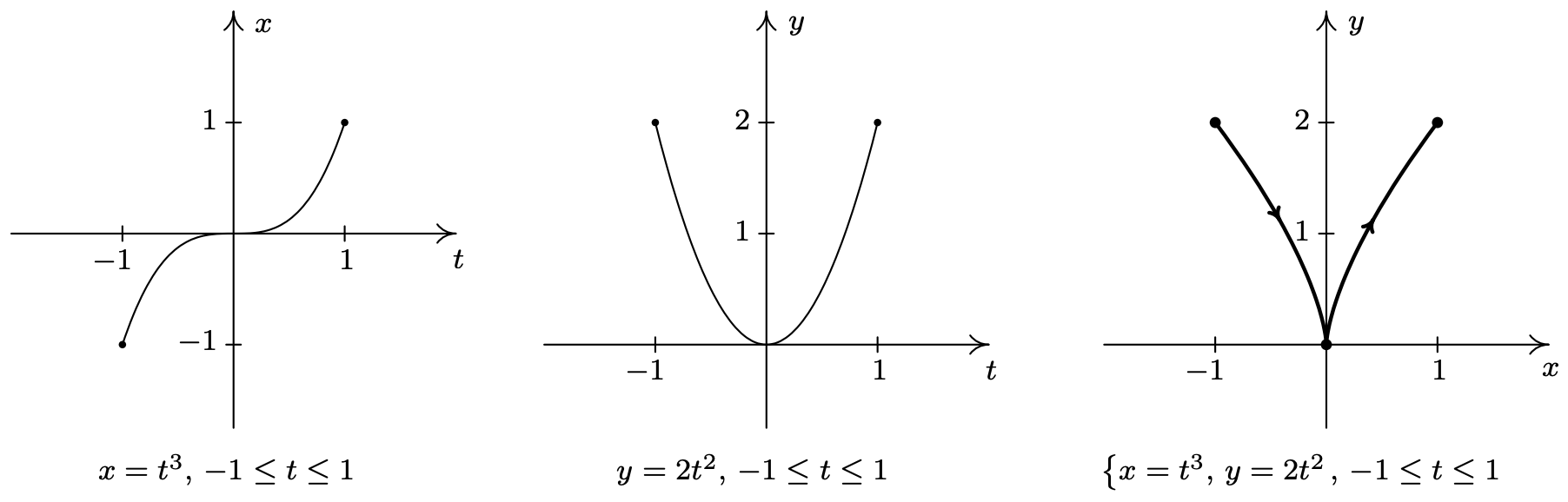
1. Para tener una idea de la curva descrita por el sistema, primero\(\left\{x=t^{3}, y=2 t^{2}\right.\) esbozamos las gráficas de\(x=t^{3}\) y\(y=2 t^{2}\) sobre el intervalo [−1, 1]. Observamos que como\(t\) toma valores en el intervalo [−1, 1],\(x=t^{3}\) oscila entre −1 y 1, y\(y=2 t^{2}\) oscila entre 0 y 2. Esto significa que toda la acción está ocurriendo en una porción del plano, a saber\(\{(x, y) \mid-1 \leq x \leq 1,0 \leq y \leq 2\}\). A continuación, trazamos algunos puntos para tener una idea de la posición y orientación de la curva. Ciertamente,\(t = −1\) y\(t = 1\) son buenos valores a elegir ya que estos son los valores extremos de\(t\). También elegimos\(t = 0\), ya que eso corresponde a un mínimo relativo ⁴ en la gráfica de\(y=2 t^{2}\). El enchufar\(t = −1\) da el punto (−1, 2),\(t = 0\) da (0, 0) y\(t = 1\) da (1, 2). De manera más general, vemos que\(x=t^{3}\) está aumentando a lo largo de todo el intervalo [−1, 1] mientras que\(y=2 t^{2}\) va disminuyendo a lo largo del intervalo [−1, 0] y luego aumentando sobre [0, 1]. Geométricamente, esto significa que para trazar el camino descrito por las ecuaciones paramétricas, comenzamos en (−1, 2) (donde\(t = −1\)), luego nos movemos hacia la derecha (ya que\(x\) está aumentando) y hacia abajo (ya que\(y\) es decreciente) a (0, 0) (donde\(t = 0\)). Seguimos moviéndonos hacia la derecha (ya que\(x\) sigue aumentando) pero ahora nos movemos hacia arriba (ya que ahora\(y\) está aumentando) hasta llegar a (1, 2) (donde\(t = 1\)). Finalmente, para tener una buena idea de la forma de la curva, eliminamos el parámetro. Resolviendo\(x=t^{3}\) para\(t\), obtenemos\(t=\sqrt[3]{x}\). Sustituyendo esto en\(y=2 t^{2}\) da\(y=2(\sqrt[3]{x})^{2}=2 x^{2 / 3}\). Nuestra experiencia en la Sección 5.3 arroja la gráfica de nuestra respuesta final a continuación.

   

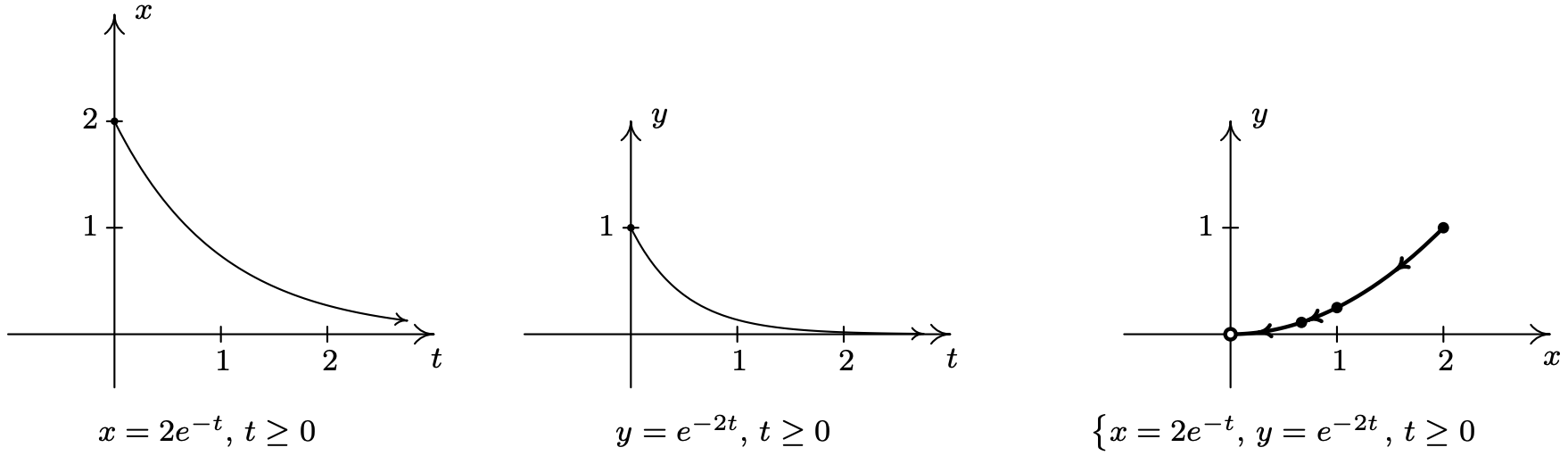
2. Para el sistema\(\left\{x=2 e^{-t}, y=e^{-2 t} \text { for } t \geq 0\right.\), procedemos como en el ejemplo anterior y graficamos\(x=2 e^{-t}\) y\(y=e^{-2 t}\) sobre el intervalo\([0, \infty)\). Encontramos que el rango de\(x\) en este caso es (0, 2] y el rango de\(y\) es (0, 1]. A continuación, conectamos algunos valores amigables de\(t\) para tener una idea de la orientación de la curva. Dado que\(t\) se encuentra en el exponente aquí, los valores 'amigables' de\(t\) involucran logaritmos naturales. Comenzando con\(t=\ln (1)=0\) obtenemos ⁵ (2, 1),\(t=\ln (2)\) porque obtenemos\(\left(1, \frac{1}{4}\right)\) y para\(t=\ln (3)\) obtenemos\ left (\ frac {2} {3},\ frac {1} {9}\ right)\). Dado que\(t\) va a lo largo del intervalo no acotado\([0, \infty)\), nos tomamos el tiempo para analizar el comportamiento final de ambos\(x\) y\(y\). \(y=e^{-2 t} \rightarrow 0^{+}\)Como\(t \rightarrow \infty, x=2 e^{-t} \rightarrow 0^{+}\) y también. Esto significa que la gráfica de\(\left\{x=2 e^{-t}, y=e^{-2 t}\right.\) se acerca al punto (0, 0). Ya que ambos\(x=2 e^{-t}\) y siempre\(y=e^{-2 t}\) están disminuyendo para\(t \geq 0\), sabemos que nuestra gráfica final comenzará en (2, 1) (donde\(t = 0\)), y se moverá consistentemente hacia la izquierda (ya que\(x\) es decreciente) y hacia abajo (ya que\(y\) es decreciente) para acercarse al origen. Para eliminar el parámetro, una forma de proceder es resolver\(x=2 e^{-t}\)\(t\) para obtener\(t=-\ln \left(\frac{x}{2}\right)\). Sustituyendo esto por\(t\) in\(y=e^{-2 t}\) da\(y=e^{-2(-\ln (x / 2))}=e^{2 \ln (x / 2)}=e^{\ln (x / 2)^{2}}=\left(\frac{x}{2}\right)^{2}=\frac{x^{2}}{4}\). O bien, podríamos reconocer eso\(y=e^{-2 t}=\left(e^{-t}\right)^{2}\), y como\(x=2 e^{-t}\) significa\(e^{-t}=\frac{x}{2}\), también conseguimos de\(y=\left(\frac{x}{2}\right)^{2}=\frac{x^{2}}{4}\) esta manera. De cualquier manera, la gráfica de\(\left\{x=2 e^{-t}, y=e^{-2 t} \text { for } t \geq 0\right.\) es una porción de la parábola\(y=\frac{x^{2}}{4}\) que comienza en el punto (2, 1) y se dirige hacia, pero nunca alcanza, ⁶ (0,0).

   

3. Para el sistema\(\{x=\sin (t), y=\csc (t) \text { for } 0<t<\pi\), comenzamos por graficar\(x=\sin (t)\) y\(y=\csc (t)\) sobre el intervalo\((0, \pi)\). Encontramos que el rango de\(x\) es (0, 1] mientras que el rango de\(y\) es\([1, \infty)\). Trazando algunos puntos amistosos, vemos que\(t=\frac{\pi}{6}\) da el punto\(\left(\frac{1}{2}, 2\right), t=\frac{\pi}{2}\) da (1,1) y nos\(t=\frac{5 \pi}{6}\) devuelve a\(\left(\frac{1}{2}, 2\right)\). Dado que\(t=0\) y\(t=\pi\) no están incluidos en el dominio for\(t\), (porque no\(y=\csc (t)\) está definido en estos\(t\) -valores), analizamos el comportamiento del sistema como\(t\) aproximación 0 y\(\pi\). Nos encontramos con eso así\(t \rightarrow 0^{+}\) como cuándo\(t \rightarrow \pi^{-}\), obtenemos\(x=\sin (t) \rightarrow 0^{+}\) y\(y=\csc (t) \rightarrow \infty\). Reuniendo toda esta información, obtenemos que por\(t\) cerca de 0, tenemos puntos con\(x\) valores positivos muy pequeños, pero\(y\) valores positivos muy grandes. A medida que los\(t\) rangos a través del intervalo\(\left(0, \frac{\pi}{2}\right], x=\sin (t)\) va en aumento y\(y=\csc (t)\) disminuye. Esto significa que nos estamos moviendo hacia la derecha y hacia abajo, a través de\(\left(\frac{1}{2}, 2\right)\) cuándo\(t=\frac{\pi}{6}\) a (1,1) cuándo\(t=\frac{\pi}{2}\). Una vez\(t=\frac{\pi}{2}\), la orientación se invierte, y empezamos a dirigirnos hacia la izquierda, ya que ahora\(x=\sin (t)\) está disminuyendo, y hacia arriba, ya que ahora\(y=\csc (t)\) va en aumento. Pasamos de\(t=\frac{5 \pi}{6}\) regreso\(\left(\frac{1}{2}, 2\right)\) cuando volvemos a los puntos con pequeñas\(x\) coordenadas positivas y grandes\(y\) coordenadas positivas. Para explicar mejor este comportamiento, eliminamos el parámetro. Usando una identidad recíproca, escribimos\(y=\csc (t)=\frac{1}{\sin (t)}\). Ya que\(x=\sin (t)\), la curva trazada por esta parametrización es una porción de la gráfica de\(y=\frac{1}{x}\). Ahora podemos explicar el comportamiento inusual como\(t \rightarrow 0^{+}\) y\(t \rightarrow \pi^{-}\) — para estos valores de\(t\), estamos abrazando la asíntota vertical\(x = 0\) de la gráfica de\(y=\frac{1}{x}\). Vemos que la parametrización dada anteriormente rastrea la porción de\(y=\frac{1}{x}\) para el\(0<x \leq 1\) doble de\(t\) corridas a través del intervalo\((0, \pi)\).

   

4. Procediendo como se indicó anteriormente, nos\(\left\{x=1+3 \cos (t), y=2 \sin (t) \text { for } 0 \leq t \leq \frac{3 \pi}{2}\right.\) propusimos graficar primero graficando\(x=1+3 \cos (t)\) y\(y=2 \sin (t)\) en el intervalo\(\left[0, \frac{3 \pi}{2}\right]\). Vemos que\(x\) va de −2 a 4 y\(y\) va de −2 a 2. La conexión\(t=0, \frac{\pi}{2}, \pi \text { and } \frac{3 \pi}{2}\) da los puntos (4, 0), (1, 2), (−2, 0) y (1, −2), respectivamente. Como\(t\) rangos de 0 a\(\frac{\pi}{2}, x=1+3 \cos (t)\) es decreciente, mientras que\(y=2 \sin (t)\) va en aumento. Esto significa que comenzamos a trazar nuestra respuesta en (4, 0) y continuamos moviéndonos hacia la izquierda y hacia arriba hacia (1, 2). Porque\(\frac{\pi}{2} \leq t \leq \pi\),\(x\) es decreciente, tal\(y\) cual, por lo que el movimiento sigue siendo de derecha a izquierda, pero ahora es hacia abajo de (1, 2) a (−2, 0). En el intervalo\(\left[\pi, \frac{3 \pi}{2}\right]\),\(x\) comienza a aumentar, mientras que\(y\) sigue disminuyendo. Por lo tanto, el movimiento se vuelve de izquierda a derecha pero continúa hacia abajo, conectando (−2, 0) a (1, −2). Para eliminar el parámetro aquí, observamos que las funciones trigonométricas involucradas, es decir\(\cos (t)\) y\(\sin (t)\), están relacionadas por la Identidad Pitagórica\(\cos ^{2}(t)+\sin ^{2}(t)=1\). De ahí, resolvemos\(x=1+3 \cos (t)\)\(\cos (t)\) para conseguir\(\cos (t)=\frac{x-1}{3}\), y resolvemos\(y=2 \sin (t)\)\(\sin (t)\) para conseguir\(\sin (t)=\frac{y}{2}\). Sustituyendo estas expresiones en\(\cos ^{2}(t)+\sin ^{2}(t)=1\) da\(\left(\frac{x-1}{3}\right)^{2}+\left(\frac{y}{2}\right)^{2}=1, \text { or } \frac{(x-1)^{2}}{9}+\frac{y^{2}}{4}=1\). De la Sección 7.4, sabemos que la gráfica de esta ecuación es una elipse centrada en (1, 0) con vértices en (−2, 0) y (4, 0) con un eje menor de longitud 4. Nuestras ecuaciones paramétricas aquí están trazando tres cuartas partes de esta elipse, en sentido contrario a las agujas del reloj.

   

Ahora que hemos tenido alguna buena práctica esbozando las gráficas de ecuaciones paramétricas, volvemos al problema de encontrar representaciones paramétricas de curvas. Empezamos con lo siguiente.

Parametrizaciones de Curvas Comunes

• Parametrizar\(y = f(x)\) como\(x\) corre a través de algún intervalo\(I\), dejar\(x = t\)\(y = f(t)\) y dejar\(t\) correr a través\(I\).
• Parametrizar\(x = g(y)\) como\(y\) corre a través de algún intervalo\(I\), dejar\(x = g(t)\)\(y = t\) y dejar\(t\) correr a través\(I\).
• Para parametrizar un segmento de línea dirigida con punto inicial\(\left(x_{0}, y_{0}\right)\) y punto terminal\(\left(x_{1}, y_{1}\right)\), let\(x=x_{0}+\left(x_{1}-x_{0}\right) t\) y\(y=y_{0}+\left(y_{1}-y_{0}\right) t\) for\(0 \leq t \leq 1\).
• Parametrizar\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) dónde\(a, b > 0\), dejar\(x=h+a \cos (t)\) y\(y=k+b \sin (t)\) para\(0 \leq t<2 \pi\). (Esto impartirá una orientación en sentido antihorario).

Se alienta al lector a verificar las fórmulas anteriores eliminando el parámetro y, cuando se indique, verificando la orientación. Ponemos a buen uso estas fórmulas en el siguiente ejemplo.

Ejemplo 11.10.3

Encuentra una parametrización para cada una de las siguientes curvas y consulta tus respuestas.

1. \(y=x^{2} \text { from } x=-3 \text { to } x=2\)
2. \(y=f^{-1}(x) \text { where } f(x)=x^{5}+2 x+1\)
3. El segmento de línea que comienza en (2, −3) y termina en (1, 5)
4. El círculo\(x^{2}+2 x+y^{2}-4 y=4\)
5. La mitad izquierda de la elipse\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)

Solución

1. Ya que\(y=x^{2}\) está escrito en la forma\(y=f(x)\), dejamos\(x = t\) y\(y=f(t)=t^{2}\). Ya que\(x = t\), los límites en\(t\) partido precisamente los límites en\(x\) así que obtenemos\(\left\{x=t, y=t^{2} \text { for }-3 \leq t \leq 2\right.\). El chequeo es casi trivial; con\(x = t\) tenemos\(y=t^{2}=x^{2}\) como\(t = x\) carreras de −3 a 2.
2. Se nos dice parametrizar\(y=f^{-1}(x)\) para\(f(x)=x^{5}+2 x+1\) así que es seguro asumir que\(f\) es uno a uno. (De lo contrario, no\(f^{-1}\) existiría.) Para encontrar una fórmula\(y=f^{-1}(x)\), seguimos el procedimiento descrito en la página 384 — comenzamos con la ecuación\(y = f(x)\), el intercambio\(x\) y\(y\) y resolvemos para\(y\). Hacerlo nos da la ecuación\(x=y^{5}+2 y+1\). Si bien podríamos intentar resolver esta ecuación para\(y\), no necesitamos hacerlo. Podemos parametrizar\(x=f(y)=y^{5}+2 y+1\) configurando\(y = t\) así que\(x=t^{5}+2 t+1\). Sabemos por nuestro trabajo en la Sección 3.1 que dado que\(f(x)=x^{5}+2 x+1\) es un polinomio de grado impar, el rango de\(y=f(x)=x^{5}+2 x+1\) es\((-\infty, \infty)\). De ahí que, para poder trazar toda la gráfica de\(x=f(y)=y^{5}+2 y+1\), necesitamos dejar\(y\) correr a través de todos los números reales. Nuestra respuesta final a este problema es\(\left\{x=t^{5}+2 t+1, y=t\right.\) para\(-\infty<t<\infty\). Al igual que en el problema anterior, nuestra solución es trivial de verificar. ⁷
3. Para parametrizar el segmento de línea que comienza en (2, −3) y termina en (1, 5), hacemos uso de las fórmulas\(x=x_{0}+\left(x_{1}-x_{0}\right) t\) y\(y=y_{0}+\left(y_{1}-y_{0}\right) t\) para\(0 \leq t \leq 1\). Si bien estas ecuaciones a primera vista son bastantes, ⁸ se pueden resumir como 'punto de partida + (desplazamiento)\(t\) '. Para encontrar la ecuación para\(x\), tenemos que el segmento de línea comienza en\(x = 2\) y termina en\(x = 1\). Esto significa que el desplazamiento en la\(x\) dirección -es (1 − 2) = −1. De ahí que la ecuación para\(x\) es\(x = 2 + (−1)t = 2 − t\). Para\(y\), observamos que el segmento de línea comienza en\(y = −3\) y termina en\(y = 5\). De ahí que el desplazamiento en la\(y\) dirección es\((5 − (−3)) = 8\), así que obtenemos\(y = −3 + 8t\). Nuestra respuesta final es\(\{x=2-t, y=-3+8 t\) para\(0 \leq t \leq 1\). Para verificar, podemos resolver\(x = 2 − t\)\(t\) para obtener\(t = 2 − x\). Sustituyendo esto en\(y = −3 + 8t\) da\(y = −3 + 8t = −3 + 8(2 − x)\), o\(y = −8x + 13. We know this is the graph of a line, so all we need to check is that it starts and stops at the correct points. When \(t = 0, x = 2 − t = 2\), y cuando\(t = 1, x = 2 − t = 1\). Enchufar\(x = 2\) da\(y = −8(2) + 13 = −3\), para un punto inicial de\((2, −3)\). El enchufar\(x = 1\) da\(y = −8(1) + 13 = 5\) para un punto final de\((1, 5)\), según sea necesario.
4. Para poder utilizar las fórmulas anteriores para parametrizar el círculo\(x^{2}+2 x+y^{2}-4 y=4\), primero tenemos que ponerlo en la forma correcta. Después de completar las plazas, obtenemos\((x+1)^{2}+(y-2)^{2}=9\), o\(\frac{(x+1)^{2}}{9}+\frac{(y-2)^{2}}{9}=1\). Una vez más, las fórmulas\(x=h+a \cos (t)\) y\(y=k+b \sin (t)\) pueden ser un reto para memorizar, pero vienen de la Identidad Pitagórica\(\cos ^{2}(t)+\sin ^{2}(t)=1\). En la ecuación\(\frac{(x+1)^{2}}{9}+\frac{(y-2)^{2}}{9}=1\), identificamos\(\cos (t)=\frac{x+1}{3}\) y\(\sin (t)=\frac{y-2}{3}\). Reordenando estas dos últimas ecuaciones, obtenemos\(x=-1+3 \cos (t)\) y\(y=2+3 \sin (t)\). Con el fin de completar una revolución alrededor del círculo, dejamos el\(t\) rango a través del intervalo\([0,2 \pi)\). Obtenemos como respuesta final\(\{x=-1+3 \cos (t), y=2+3 \sin (t)\) para\(0 \leq t<2 \pi\). Para verificar nuestra respuesta, podríamos eliminar el parámetro resolviendo\(x=-1+3 \cos (t)\) para\(\cos (t)\) y\(y=2+3 \sin (t)\) para\(\sin (t)\), invocando una Identidad Pitagórica, y luego manipulando la ecuación resultante\(y\) dentro\(x\) y dentro de la ecuación original\(x^{2}+2 x+y^{2}-4 y=4\). En cambio, optamos por un enfoque más directo. Nosotros sustituimos\(x=-1+3 \cos (t)\) y\(y=2+3 \sin (t)\) en la ecuación\(x^{2}+2 x+y^{2}-4 y=4\) y demostramos que esta última está satisfecha para todos\(t\) tales que\(0 \leq t<2 \pi\). \[\begin{array}{rlll} x^{2}+2 x+y^{2}-4 y & = & 4 \\ (-1+3 \cos (t))^{2}+2(-1+3 \cos (t))+(2+3 \sin (t))^{2}-4(2+3 \sin (t)) & \stackrel{?}{=} & 4 \\ 1-6 \cos (t)+9 \cos ^{2}(t)-2+6 \cos (t)+4+12 \sin (t)+9 \sin ^{2}(t)-8-12 \sin (t) & \stackrel{?}{=} & 4 \\ 9 \cos ^{2}(t)+9 \sin ^{2}(t)-5 & \stackrel{?}{=} & 4 \\ 9\left(\cos ^{2}(t)+\sin ^{2}(t)\right)-5 & \stackrel{?}{=} & 4 \\ 9(1) -5 & \stackrel{?}{=} & 4 \\ 4 &\stackrel{\checkmark}{=} & 4 \end{array}\nonumber\]Ahora que sabemos que las ecuaciones paramétricas nos dan puntos en el círculo, podemos pasar por el análisis habitual como se demuestra en el Ejemplo 11.10.2 para mostrar que todo el círculo está cubierto como\(t\) rangos a través del intervalo\([0,2 \pi)\).
5. En la ecuación\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\), podemos usar las fórmulas anteriores o pensar en la Identidad pitagórica para obtener\(x=2 \cos (t)\) y\(y=3 \sin (t)\). El rango normal sobre el parámetro en este caso es\(0 \leq t<2 \pi\), pero como nos interesa sólo la mitad izquierda de la elipse, restringimos a los valores que corresponden\(t\) a los ángulos del Cuadrante II y del Cuadrante III, a saber\(\frac{\pi}{2} \leq t \leq \frac{3 \pi}{2}\). Nuestra respuesta final es\(\{x=2 \cos (t), y=3 \sin (t)\) para\(\frac{\pi}{2} \leq t \leq \frac{3 \pi}{2}\). Sustituyendo\(x=2 \cos (t)\) y\(y=3 \sin (t)\) en\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) da\(\frac{4 \cos ^{2}(t)}{4}+\frac{9 \sin ^{2}(t)}{9}=1\), lo que reduce a la Identidad Pitagórica\(\cos ^{2}(t)+\sin ^{2}(t)=1\). Esto demuestra que los puntos generados por las ecuaciones paramétricas se\(\{x=2 \cos (t), y=3 \sin (t)\) encuentran en la elipse\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\). Empleando las técnicas demostradas en el Ejemplo 11.10.2, encontramos que la restricción\(\frac{\pi}{2} \leq t \leq \frac{3 \pi}{2}\) genera la mitad izquierda de la elipse, según se requiera.

Observamos que las fórmulas dadas en la página 1053 ofrecen solo una de literalmente infinitamente muchas formas de parametrizar las curvas comunes enumeradas allí. En ocasiones, las fórmulas que allí se ofrecen necesitan ser alteradas para adecuarse a la situación. A continuación se dan dos formas fáciles de alterar las parametrizaciones.

Ajuste de ecuaciones paramétricas

• Orientación de inversión: Reemplazar cada ocurrencia de\(t\) con\(−t\) en una descripción paramétrica para una curva (incluyendo cualquier desigualdad que describa los límites en\(t\)) invierte la orientación de la curva.
• Desplazamiento del parámetro: Reemplazar cada ocurrencia de\(t\) con\((t − c)\) en una descripción paramétrica para una curva (incluyendo cualquier desigualdad que describa los límites en\(t\)) desplaza el inicio del parámetro\(t\) adelante por\(c\) unidades.

Demostramos estas técnicas en el siguiente ejemplo.

Ejemplo 11.10.4

Encuentra una parametrización para las siguientes curvas.

1. La curva que comienza en (2, 4) y sigue la parábola\(y=x^{2}\) para terminar en (−1, 1). Desplace el parámetro para que la ruta comience en\(t = 0\).
2. El camino de dos partes que comienza en (0, 0), viaja a lo largo de una línea hasta (3, 4), luego viaja a lo largo de una línea hasta (5, 0).
3. El Círculo de Unidad, orientado en sentido horario, con\(t = 0\) correspondiente a (0, −1).

Solución

1. Podemos parametrizar\(y=x^{2}\) desde\(x = −1\) hasta\(x = 2\) usando la fórmula dada en la Página 1053 en\(\left\{x=t, y=t^{2}\right.\) cuanto a\(-1 \leq t \leq 2\). Esta parametrización, sin embargo, comienza en (−1, 1) y termina en (2, 4). De ahí que necesitamos revertir la orientación. Para ello, reemplazamos cada ocurrencia de\(t\) por\(−t\) para obtener\(\left\{x=-t, y=(-t)^{2}\right.\) para\(-1 \leq-t \leq 2\). Después de simplificar, obtenemos\(\left\{x=-t, y=t^{2}\right.\) para\(-2 \leq t \leq 1\). Nos gustaría\(t\) comenzar en\(t = 0\) vez de\(t = −2\). El problema aquí es que la parametrización que tenemos inicia 2 unidades 'demasiado pronto', por lo que necesitamos introducir un 'retraso de tiempo' de 2. Reemplazar cada ocurrencia de\(t\) con\((t-2)\) da\(\left\{x=-(t-2), y=(t-2)^{2}\right.\) para\(-2 \leq t-2 \leq 1\). Simplificando los rendimientos\(\left\{x=2-t, y=t^{2}-4 t+4 \text { for } 0 \leq t \leq 3\right.\).
2. Al parametrizar segmentos de línea, pensamos: 'punto de partida + (desplazamiento)\(t\) '. Para la primera parte del camino, obtenemos\(\{x=3 t, y=4 t\) para\(0 \leq t \leq 1\), y para la segunda parte obtenemos\(\{x=3+2 t, y=4-4 t\) para\(0 \leq t \leq 1\). Dado que la primera parametrización deja en\(t = 1\), cambiamos el parámetro en la segunda parte para que comience en\(t = 1\). Nuestra descripción actual de la segunda parte comienza en\(t = 0\), por lo que introducimos un 'retraso de tiempo' de 1 unidad al segundo conjunto de ecuaciones paramétricas. Reemplazar\(t\) con\((t − 1)\) en el segundo conjunto de ecuaciones paramétricas da\(\{x=3+2(t-1), y=4-4(t-1)\) para\(0 \leq t-1 \leq 1\). Simplificando los rendimientos\(\{x=1+2 t, y=8-4 t\) para\(1 \leq t \leq 2\). Por lo tanto, podemos parametrizar el camino en\(\{x=f(t), y=g(t)\) cuanto a\(0 \leq t \leq 2\) dónde\[f(t)=\left\{\begin{aligned} 3 t, & \text { for } 0 \leq t \leq 1 \\ 1+2 t, & \text { for } 1 \leq t \leq 2 \end{aligned} \quad \text { and } \quad g(t)=\left\{\begin{aligned} 4 t, & \text { for } 0 \leq t \leq 1 \\ 8-4 t, & \text { for } 1 \leq t \leq 2 \end{aligned}\right.\right.\nonumber\]
3. Sabemos que\(\{x=\cos (t), y=\sin (t)\) para\(0 \leq t<2 \pi\) da una parametrización en sentido antihorario del Círculo de Unidad con\(t = 0\) correspondiente a (1, 0), por lo que el primer orden del día es revertir la orientación. Sustituir\(t\) con\(−t\) da\(\{x=\cos (-t), y=\sin (-t)\) para\(0 \leq-t<2 \pi\), lo que simplifica ⁹ a\(\{x=\cos (t), y=-\sin (t)\) para\(-2 \pi<t \leq 0\). Esta parametrización da una orientación en el sentido de las agujas del reloj, pero\(t = 0\) aún corresponde al punto (1, 0); el punto (0, −1) se alcanza cuando\(t=-\frac{3 \pi}{2}\). Nuestra estrategia es primero obtener la parametrización para 'comenzar' en el punto (0, −1) y luego desplazar el parámetro en consecuencia para que el 'inicio' coincida con\(t = 0\). Sabemos que cualquier intervalo de longitud\(2\pi\) parametrizará todo el círculo, así que mantenemos las ecuaciones\(\{x=\cos (t), y=-\sin (t)\), pero iniciamos el parámetro\(t\) en\(-\frac{3 \pi}{2}\), y encontramos el límite superior sumando\(2\pi\) así\(-\frac{3 \pi}{2} \leq t<\frac{\pi}{2}\). El lector puede verificar que\(\{x=\cos (t), y=-\sin (t)\) para\(-\frac{3 \pi}{2} \leq t<\frac{\pi}{2}\) trazas el Círculo de Unidad en el sentido de las agujas del reloj comenzando en el punto (0, −1). Ahora cambiamos el parámetro introduciendo un 'retraso de tiempo' de\(\frac{3 \pi}{2}\) unidades reemplazando cada ocurrencia de\(t\) con\(\left(t-\frac{3 \pi}{2}\right)\). Obtenemos\(\left\{x=\cos \left(t-\frac{3 \pi}{2}\right), y=-\sin \left(t-\frac{3 \pi}{2}\right)\right.\) para\(-\frac{3 \pi}{2} \leq t-\frac{3 \pi}{2}<\frac{\pi}{2}\). Esto simplifica ¹⁰ a\(\{x=-\sin (t), y=-\cos (t)\) para\(0 \leq t<2 \pi\), según sea necesario.

Ponemos a buen uso nuestra respuesta al Ejemplo 11.10.4 número 3 para derivar la ecuación de un cicloide. Supongamos que un círculo de radio\(r\) rueda a lo largo del\(x\) eje positivo a una velocidad constante\(v\) como se muestra a continuación. \(\theta\)Sea el ángulo en radianes que mide la cantidad de rotación en sentido horario experimentada por el radio resaltado en la figura.

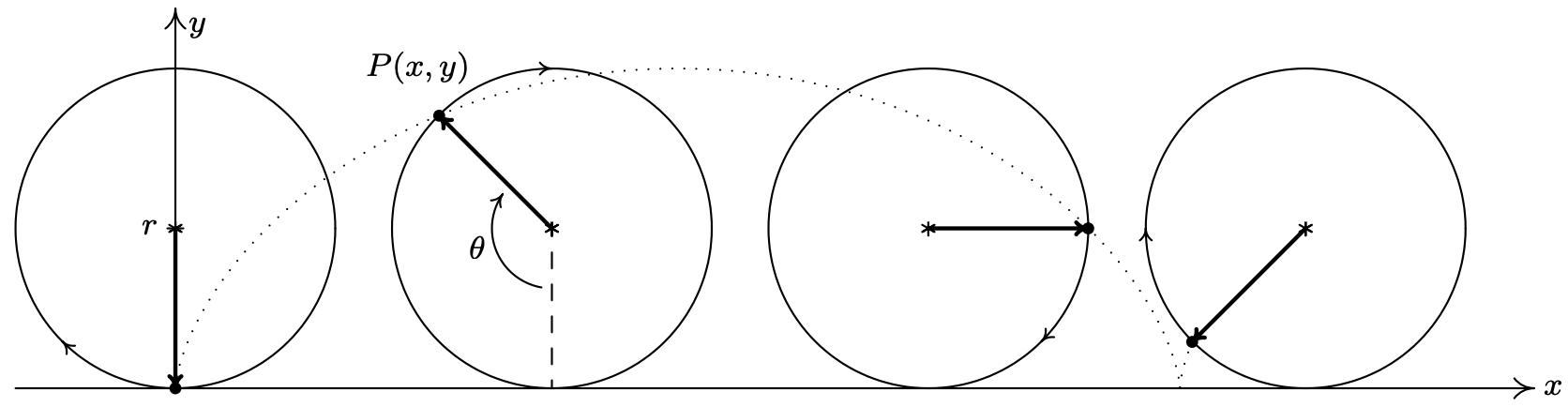
Nuestro objetivo es encontrar ecuaciones paramétricas para las coordenadas del punto\(P(x, y)\) en términos de\(\theta\). De nuestro trabajo en el Ejemplo 11.10.4 número 3, sabemos que el movimiento en el sentido de las agujas del reloj a lo largo del Círculo Unitario comenzando en el punto (0, −1) puede ser modelado por las ecuaciones\(\{x=-\sin (\theta), y=-\cos (\theta)\) para\(0 \leq \theta<2 \pi\). (Hemos renombrado el parámetro '\(\theta\)' para que coincida con el contexto de este problema.) Para modelar este movimiento en un círculo de radio\(r\), todo lo que necesitamos hacer ¹¹ es multiplicar ambos\(x\) y\(y\) por el factor\(r\) que rinde\(\{x=-r \sin (\theta), y=-r \cos (\theta)\). Ahora necesitamos ajustarnos por el hecho de que el círculo no es estacionario con el centro (0, 0), sino que está rodando a lo largo del\(x\) eje positivo. Dado que la velocidad\(v\) es constante, sabemos que en el momento\(t\), el centro del círculo ha recorrido una\(vt\) distancia por el\(x\) eje positivo. Además, dado que el radio del círculo es\(r\) y el círculo no se mueve verticalmente, sabemos que el centro del círculo es siempre\(r\) unidades por encima del\(x\) eje -eje. Al juntar estos dos hechos, tenemos que en el momento\(t\), el centro del círculo está en ese punto\((vt, r)\). De la Sección 10.1.1, sabemos\(v=\frac{r \theta}{t}\), o\(v t=r \theta\). De ahí que el centro del círculo, en términos del parámetro\(\theta\), sea\((r \theta, r)\). Como resultado, necesitamos modificar las ecuaciones\(\{x=-r \sin (\theta), y=-r \cos (\theta)\) desplazando la\(x\) coordenada -a las\(r \theta\) unidades correctas (sumando\(r \theta\) a la expresión for\(x\)) y las\(r\) unidades\(y\) -coordenada hacia arriba ¹² (sumando\(r\) a la expresión para\(y\)). Obtenemos\(\{x=-r \sin (\theta)+r \theta, y=-r \cos (\theta)+r\), que se puede escribir como\(\{x=r(\theta-\sin (\theta)), y=r(1-\cos (\theta))\). Dado que la moción comienza en\(\theta=0\) y procede indefinidamente, nos fijamos\(\theta \geq 0\).

Terminamos la sección con una demostración de la calculadora gráfica.

Ejemplo 11.10.5

Encuentre las ecuaciones paramétricas de un cicloide que resulta de un círculo de radio 3 rodando por el\(x\) eje positivo como se describió anteriormente. Grafica tu respuesta usando una calculadora.

Solución

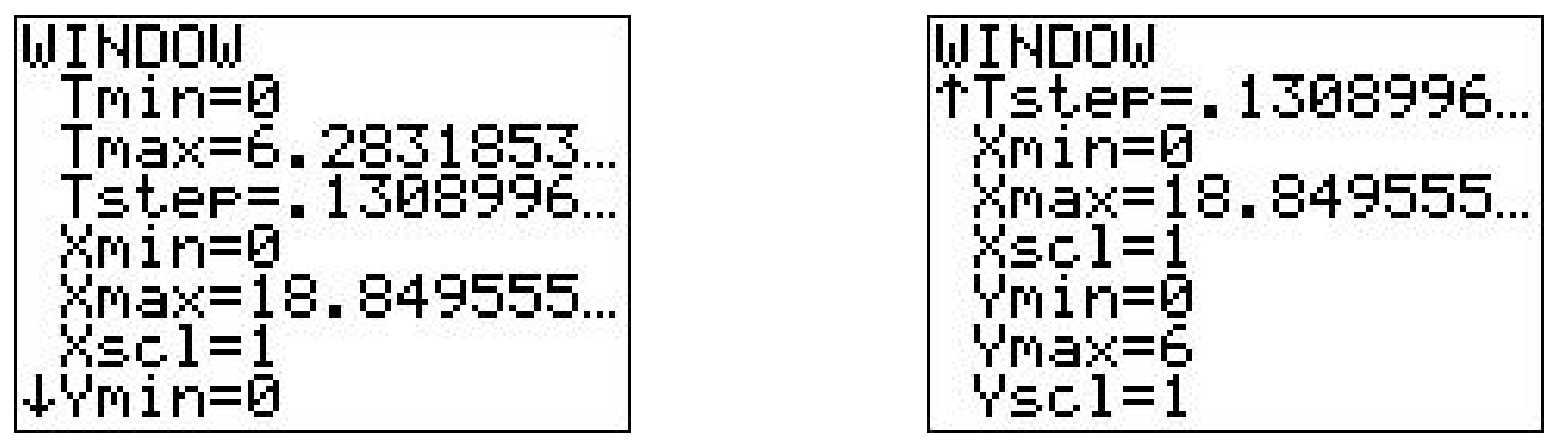
Tenemos\(r = 3\) lo que da las ecuaciones\(\{x=3(t-\sin (t)), y=3(1-\cos (t))\) para\(t \geq 0\). (Aquí hemos vuelto a la convención de usar\(t\) como parámetro.) Dibujar el cicloide a mano es un ejercicio maravilloso en Cálculo, pero para los fines de este libro, utilizamos una utilidad gráfica. Usar una calculadora para graficar ecuaciones paramétricas es muy similar a graficar ecuaciones polares en una calculadora. ¹³ Asegurando que la calculadora esté en 'Modo Paramétrico' y 'modo radián' ingresamos a las ecuaciones y avanzamos a la pantalla de 'Ventana'.

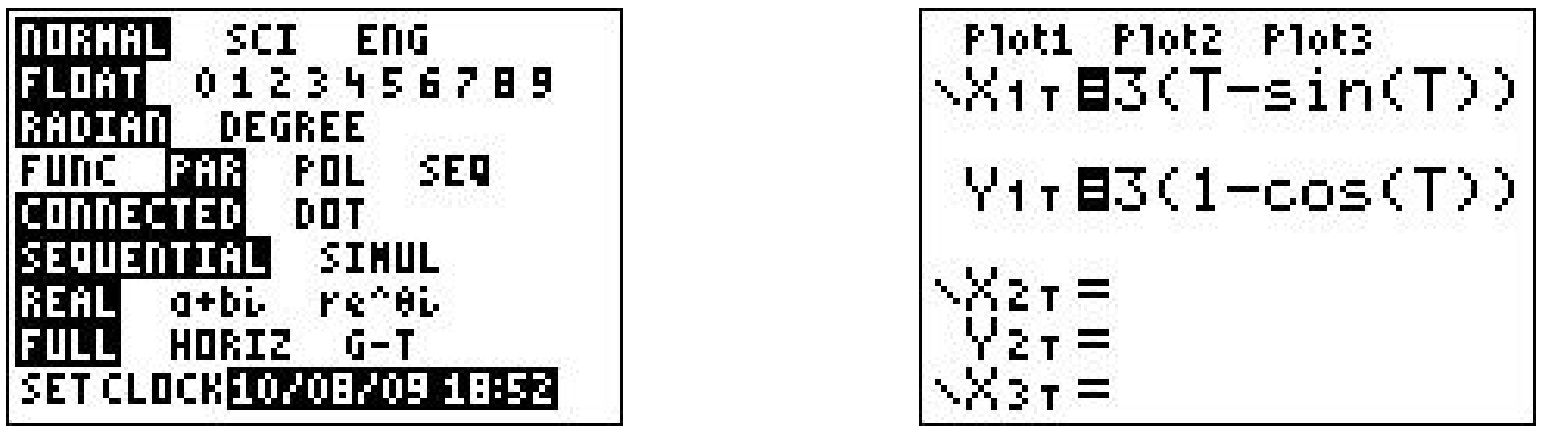
Como siempre, el reto es determinar los límites apropiados sobre el parámetro,\(t\), así como para\(x\) y\(y\). Sabemos que una revolución completa del círculo se produce a lo largo del intervalo\(0 \leq t<2 \pi\), por lo que parece razonable mantenerlos como nuestros límites\(t\). El 'Tstep' parece razonablemente pequeño — un valor demasiado grande aquí puede llevar a gráficas incorrectas. ¹⁴ Sabemos por nuestra derivación de las ecuaciones del cicloide que el centro del círculo generador tiene coordenadas\((r \theta, r)\), o en este caso,\((3 t, 3)\). Dado que\(t\) rangos entre 0 y\(2 \pi\), establecemos\(x\) un rango entre 0 y\(6 \pi\). Los valores de\(y\) van desde la parte inferior del círculo hasta la parte superior, por lo que\(y\) oscila entre 0 y 6.

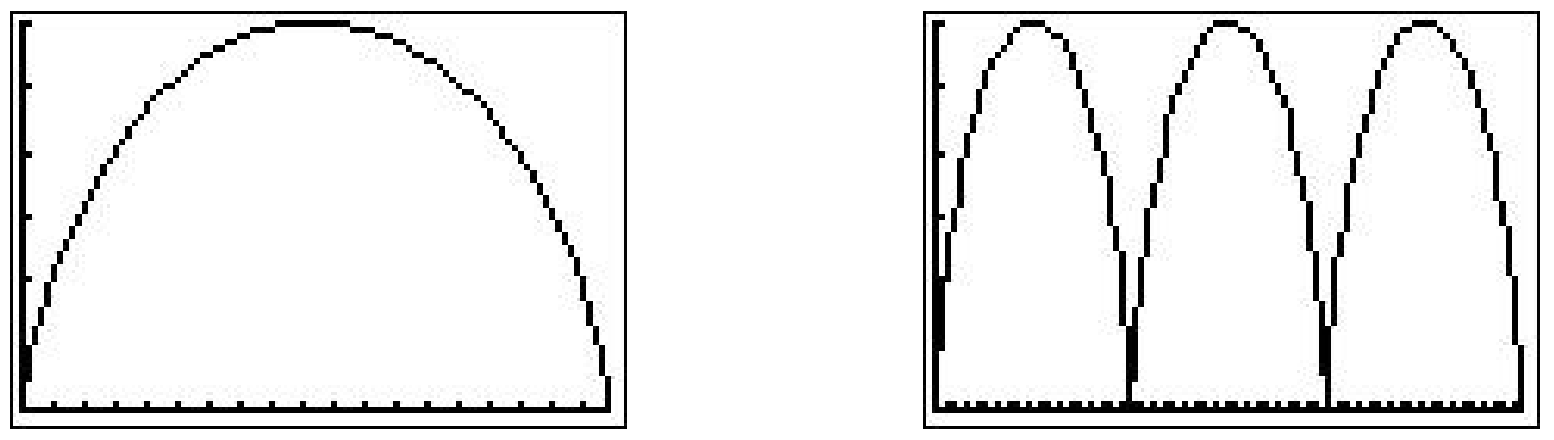
A continuación graficamos el cicloide con estos ajustes, para luego extendernos\(t\) hasta el rango de 0\(x\) a\(6\pi\) lo que las fuerzas van desde 0 hasta\(18\pi\) producir tres arcos del cicloide. (Es instructivo observar que mantener los\(y\) ajustes entre 0 y 6 estropea la geometría del cicloide. Se invita al lector a utilizar la función Zoom Square en la calculadora gráfica para ver qué ventana da una verdadera perspectiva geométrica de los tres arcos.)

11.10.1 Ejercicios

En los Ejercicios 1 - 20, trazar el conjunto de ecuaciones paramétricas a mano. Asegúrese de indicar la orientación impartida en la curva por la parametrización.

1. \ (\ left\ {\ begin {array} {l}
   x=4 t-3\\
   y=6 t-2
   \ end {array}\ text {for} 0\ leq t\ leq 1\ right.\)
2. \ (\ left\ {\ begin {array} {l}
   x=4 t-1\
   y=3-4 t
   \ end {array}\ text {for} 0\ leq t\ leq 1\ right.\)
3. \ (\ left\ {\ begin {array} {l}
   x=2 t\\
   y=t^ {2}
   \ end {array}\ text {for} -1\ leq t\ leq 2\ derecha.\)
4. \ (\ izquierda\ {\ begin {array} {l}
   x=t-1\
   y=3+2 t-t^ {2}
   \ end {array}\ quad\ text {for} 0\ leq t\ leq 3\ derecha.\)
5. \ (\ left\ {\ begin {array} {l}
   x=t^ {2} +2 t+1\\
   y=t+1
   \ end {array}\ text {for} t\ leq 1\ right.\)
6. \(\begin{cases}x=\frac{1}{9}\left(18-t^{2}\right) & \text { for } t \geq-3 \\ y=\frac{1}{3} t & \end{cases}\)
7. \ (\ left\ {\ begin {array} {l}
   x=t\\
   y=t^ {3}
   \ end {array}\ text {for} -\ infty<t<\ infty\ right.\)
8. \ (\ left\ {\ begin {array} {l}
   x=t^ {3}\\
   y=t
   \ end {array}\ text {for} -\ infty<t<\ infty\ right.\)
9. \ (\ left\ {\ begin {array} {l}
   x=\ cos (t)\\
   y=\ sin (t)
   \ end {array}\ text {for} -\ frac {\ pi} {2}\ leq t\ leq\ frac {\ pi} {2}\ derecho.\)
10. \ (\ izquierda\ {\ begin {array} {l}
    x=3\ cos (t)\\
    y=3\ sin (t)
    \ end {array}\ text {for} 0\ leq t\ leq\ pi\ derecha.\)
11. \ (\ left\ {\ begin {array} {l}
    x=-1+3\ cos (t)\\
    y=4\ sin (t)
    \ end {array}\ quad\ text {for} 0\ leq t\ leq 2\ pi\ derecha.\)
12. \ (\ izquierda\ {\ begin {array} {l}
    x=3\ cos (t)\\
    y=2\ sin (t) +1
    \ end {array}\ text {for}\ frac {\ pi} {2}\ leq t\ leq 2\ pi\ derecha.\)
13. \ (\ left\ {\ begin {array} {l}
    x=2\ cos (t)\\
    y=\ sec (t)
    \ end {array}\ text {for} 0\ leq t<\ frac {\ pi} {2}\ right.\)
14. \ (\ left\ {\ begin {array} {l}
    x=2\ tan (t)\\
    y=\ cot (t)
    \ end {array}\ text {for} 0<t<\ frac {\ pi} {2}\ right.\)
15. \ (\ izquierda\ {\ begin {array} {l}
    x=\ sec (t)\\
    y=\ tan (t)
    \ end {array}\ text {for} -\ frac {\ pi} {2} <t<\ frac {\ pi} {2}\ derecha.\)
16. \ (\ izquierda\ {\ begin {array} {l}
    x=\ sec (t)\\
    y=\ tan (t)
    \ end {array}\ text {for}\ frac {\ pi} {2} <t<\ frac {3\ pi} {2}\ derecha.\)
17. \ (\ izquierda\ {\ begin {array} {l}
    x=\ tan (t)\\
    y=2\ seg (t)
    \ end {array}\ text {for} -\ frac {\ pi} {2} <t<\ frac {\ pi} {2}\ derecha.\)
18. \ (\ izquierda\ {\ begin {array} {l}
    x=\ tan (t)\\
    y=2\ seg (t)
    \ end {array}\ text {for}\ frac {\ pi} {2} <t<\ frac {3\ pi} {2}\ derecha.\)
19. \ (\ left\ {\ begin {array} {l}
    x=\ cos (t)\\
    y=t
    \ end {array}\ quad\ text {for} 0\ leq t\ leq\ pi\ right.\)
20. \ (\ left\ {\ begin {array} {l}
    x=\ sin (t)\\
    y=t
    \ end {array}\ text {for} -\ frac {\ pi} {2}\ leq t\ leq\ frac {\ pi} {2}\ derecha.\)

En los Ejercicios 21 - 24, trazar el conjunto de ecuaciones paramétricas con la ayuda de una utilidad gráfica. Asegúrese de indicar la orientación impartida en la curva por la parametrización.

21. \ (\ izquierda\ {\ begin {array} {l}
    x=t^ {3} -3 t\\
    y=t^ {2} -4
    \ end {array}\ text {for} -2\ leq t\ leq 2\ derecha.\)
22. \ (\ izquierda\ {\ begin {array} {l}
    x=4\ cos ^ {3} (t)\\
    y=4\ sin ^ {3} (t)
    \ end {array}\ text {for} 0\ leq t\ leq 2\ pi\ derecha.\)
23. \ (\ left\ {\ begin {array} {l}
    x=e^ {t} +e^ {-t}\\
    y=e^ {t} -e^ {-t}
    \ end {array}\ text {for} -2\ leq t\ leq 2\ derecho.\)
24. \ (\ izquierda\ {\ begin {array} {l}
    x=\ cos (3 t)\\
    y=\ sin (4 t)
    \ end {array}\ text {for} 0\ leq t\ leq 2\ pi\ derecha.\)

En Ejercicios 25 - 39, encuentra una descripción paramétrica para la curva orientada dada.

25. el segmento de línea dirigido de (3, −5) a (−2, 2)
26. el segmento de línea dirigido de (−2, −1) a (3, −4)
27. la curva\(y=4-x^{2}\) de (−2, 0) a (2, 0).
28. la curva\(y=4-x^{2}\) de (−2, 0) a (2, 0) (Desplazar el parámetro así\(t = 0\) corresponde a (−2, 0).)
29. la curva\(x=y^{2}-9\) de (−5, −2) a (0, 3).
30. la curva\(x=y^{2}-9\) de (0, 3) a (−5, −2). (Desplazar el parámetro para que\(t = 0\) corresponda a (0, 3).)
31. el círculo\(x^{2}+y^{2}=25\), orientado en sentido antihorario
32. el círculo\((x-1)^{2}+y^{2}=4\), orientado en sentido antihorario
33. el círculo\(x^{2}+y^{2}-6 y=0\), orientado en sentido antihorario
34. el círculo\(x^{2}+y^{2}-6 y=0\), orientado a las agujas del reloj

    (Desplazar el parámetro para que t comience en 0.)

35. el círculo\((x-3)^{2}+(y+1)^{2}=117\), orientado en sentido antihorario
36. la elipse\((x-1)^{2}+9 y^{2}=9\), orientada en sentido antihorario
37. la elipse\(9 x^{2}+4 y^{2}+24 y=0\), orientada en sentido antihorario
38. la elipse\(9 x^{2}+4 y^{2}+24 y=0\), orientada hacia la derecha (Desplazar el parámetro así\(t = 0\) corresponde a (0, 0).)
39. el triángulo con vértices (0, 0), (3, 0), (0, 4), orientado en sentido antihorario (Desplazar el parámetro para que t = 0 corresponda a (0, 0).)
40. Utilice ecuaciones paramétricas y una utilidad gráfica para graficar la inversa de\(f(x)=x^{3}+3 x-4\).
41. Cada curva polar se\(r=f(\theta)\) puede traducir a un sistema de ecuaciones paramétricas con parámetro\(\theta\) by\(\{x=r \cos (\theta)=f(\theta) \cos (\theta), y=r \sin (\theta)=f(\theta) \sin (\theta)\). Convertir\(r=6 \cos (2 \theta)\) a un sistema de ecuaciones paramétricas. Comprueba tu respuesta\(r=6 \cos (2 \theta)\) graficando a mano usando las técnicas presentadas en la Sección 11.5 y luego graficando las ecuaciones paramétricas que encontraste usando una utilidad gráfica.
42. Usa tus resultados de los Ejercicios 3 y 4 de la Sección 11.1 para encontrar las ecuaciones paramétricas que modelan la posición de un pasajero mientras viaja en el London Eye.

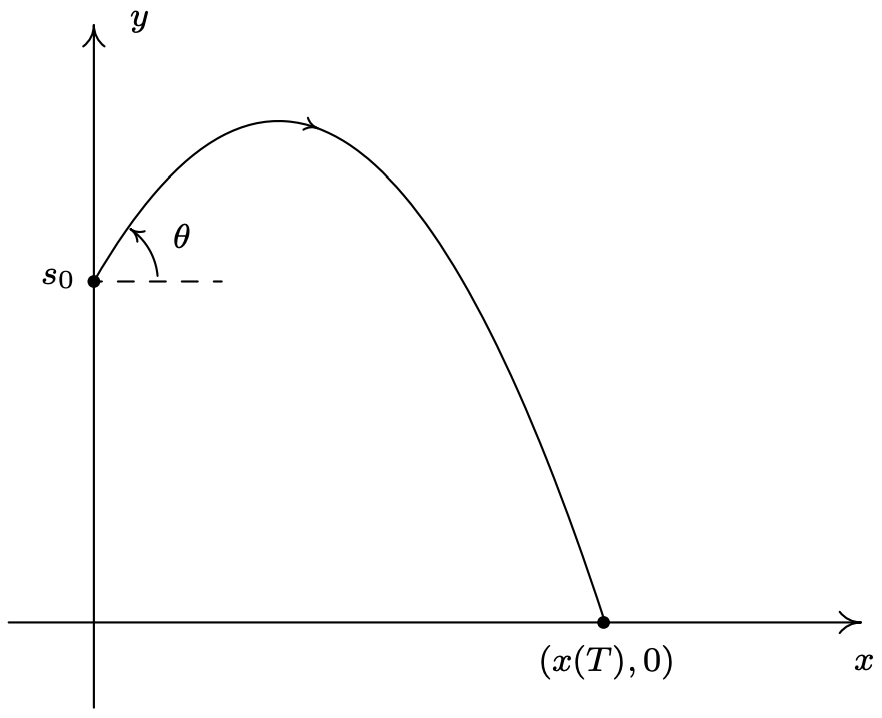
Supongamos que un objeto, llamado proyectil, es lanzado al aire. Ignorando todo excepto la fuerza gravedad, el camino del proyectil viene dado por ¹⁵

\[\left\{\begin{array}{l} x=v_{0} \cos (\theta) t \\ y=-\frac{1}{2} g t^{2}+v_{0} \sin (\theta) t+s_{0} \end{array} \quad \text { for } 0 \leq t \leq T\right.\nonumber\]

donde\(v_{0}\) esta la velocidad inicial del objeto,\(\theta\) es el angulo desde la horizontal a la que se lanza el proyectil, ¹⁶\(g\) es la aceleracion por gravedad,\(\mathcal{s}_{0}\) es la altura inicial del proyectil sobre el suelo y\(T\) es el tiempo cuando el objeto regresa al suelo. (Ver la figura a continuación.)

43. Jason, el amigo de Carl, compite en las competiciones de Highland Games en todo el país. En un evento, el 'lanzamiento de martillo', lanza un peso de 56 libras para distancia. Si el peso se libera a 6 pies sobre el suelo en un ángulo de\(42^{\circ}\) con respecto a la horizontal con una velocidad inicial de 33 pies por segundo, encuentre las ecuaciones paramétricas para el vuelo del martillo. (Aquí, use\(g=32 \frac{\mathrm{ft.}}{s^{2}}.\)) ¿Cuándo golpeará el martillo contra el suelo? ¿A qué distancia chocará contra el suelo? Comprueba tu respuesta usando una utilidad gráfica.
44. Eliminar el parámetro en las ecuaciones para el movimiento del proyectil para mostrar que la trayectoria del proyectil sigue la curva\[y=-\frac{g \sec ^{2}(\theta)}{2 v_{0}^{2}} x^{2}+\tan (\theta) x+s_{0}\nonumber\] Usa la fórmula del vértice (Ecuación 2.4) para mostrar la altura máxima del proyectil es\[y=\frac{v_{0}^{2} \sin ^{2}(\theta)}{2 g}+s_{0} \quad \text { when } \quad x=\frac{v_{0}^{2} \sin (2 \theta)}{2 g}\nonumber\]
45. En otro evento, el 'lanzamiento de gavilla', Jason lanza un peso de 20 libras por altura. Si el peso se libera a 5 pies sobre el suelo en un ángulo de\(85^{\circ}\) con respecto a la horizontal y la gavilla alcanza una altura máxima de 31.5 pies, usa tus resultados de la parte 44 para determinar qué tan rápido se lanzó la gavilla al aire. (Una vez más, use\(g=32 \frac{\mathrm{ft.}}{s^{2}}.\))
46. Supongamos\(\theta=\frac{\pi}{2}\). (El proyectil fue lanzado verticalmente). Simplifique la fórmula paramétrica general dada para\(y(t)\) arriba usando\(g=9.8 \frac{\mathrm{m}}{\mathrm{s}^{2}}\) y compárela con la fórmula para\(s(t)\) dada en el Ejercicio 25 en la Sección 2.3. ¿Qué hay\(x(t)\) en este caso?

En los Ejercicios 47 - 52, exploramos la función coseno hiperbólica, denotada\(\cosh (t)\), y la función sinusoidal hiperbólica, denotada\(\sinh(t)\), definida a continuación:\[\cosh (t)=\frac{e^{t}+e^{-t}}{2} \quad \text { and } \quad \sinh (t)=\frac{e^{t}-e^{-t}}{2}\nonumber\]

47. Usando una utilidad gráfica según sea necesario, verificar que el dominio de\(\cosh(t)\) es\((-\infty, \infty)\) y el rango de\(\cosh(t)\) es\([1, \infty)\).
48. Usando una utilidad gráfica según sea necesario, verifique que el dominio y el rango de\(\sinh(t)\) sean ambos\((-\infty, \infty)\).
49. Demostrar que\(\{x(t)=\cosh (t), y(t)=\sinh (t)\) parametrizar la mitad derecha de la hipérbola 'unidad'\(x^{2}-y^{2}=1\). (De ahí el uso del adjetivo 'hiperbólico.')
50. Comparar las definiciones de\(\cosh(t)\) y\(\sinh(t)\) con las fórmulas para\(\cos(t)\) y\(\sin(t)\) dadas en el Ejercicio 83f en la Sección 11.7.
51. Otras cuatro funciones hiperbólicas están a la espera de ser definidas: la secante hiperbólica\(\operatorname{sech}(t)\), la cosecante hiperbólica\(\operatorname{csch}(t)\), la tangente hiperbólica\(\tanh (t)\) y la cotangente hiperbólica\(\operatorname{coth}(t)\). Definir estas funciones en términos de\(\cosh (t)\) y\(\sinh (t)\), luego convertirlas en fórmulas que involucren\(e^{t}\) y\(e^{-t}\). Consulte una referencia adecuada (un libro de Cálculo, o esta entrada sobre las funciones hiperbólicas) y dedique algún tiempo a revivir la emoción de la trigonometría con estas funciones 'hiperbólicas'.
52. Si estas funciones le parecen familiares, deberían. Disfrute de cierta nostalgia y vuelva a visitar el Ejercicio 35 en la Sección 6.5, el Ejercicio 47 en la Sección 6.3 y la respuesta al Ejercicio 38 en la Sección 6.4.

11.10.2 Respuestas

1. \(\left\{\begin{array}{l} x=4 t-3 \\ y=6 t-2 \end{array} \text { for } 0 \leq t \leq 1\right.\)

   

2. \(\left\{\begin{array}{l} x=4 t-1 \\ y=3-4 t \end{array} \text { for } 0 \leq t \leq 1\right.\)

   

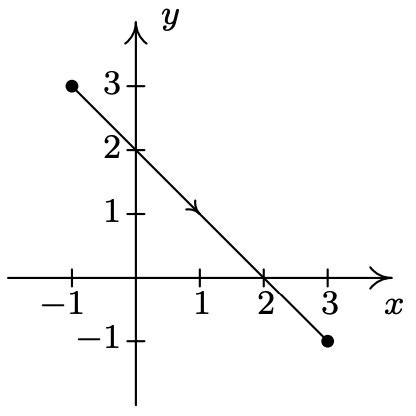
3. \(\left\{\begin{array}{l} x=2 t \\ y=t^{2} \end{array} \text { for }-1 \leq t \leq 2\right.\)

   

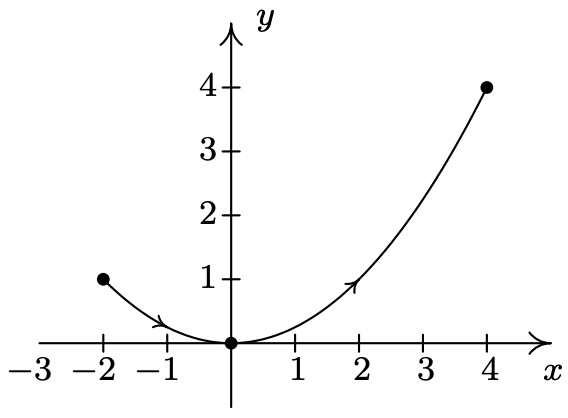
4. \(\left\{\begin{array}{l} x=t-1 \\ y=3+2 t-t^{2} \end{array} \quad \text { for } 0 \leq t \leq 3\right.\)

   

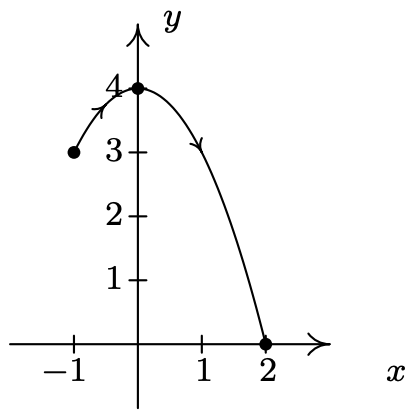
5. \(\left\{\begin{array}{l} x=t^{2}+2 t+1 \\ y=t+1 \end{array} \text { for } t \leq 1\right.\)

   

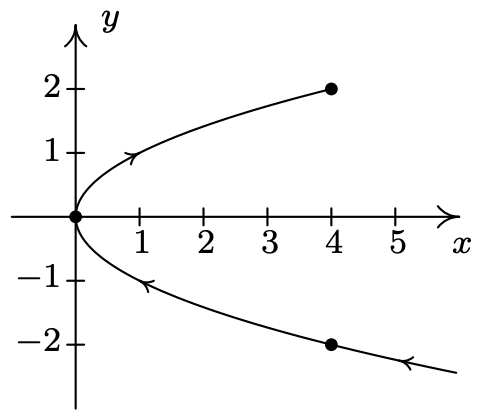
6. \(\left\{\begin{array}{l} x=\frac{1}{9}\left(18-t^{2}\right) \\ y=\frac{1}{3} t \end{array} \text { for } t \geq-3\right.\)

   

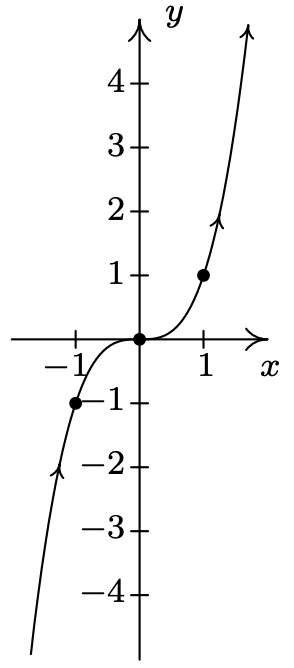
7. \(\left\{\begin{array}{l} x=t \\ y=t^{3} \end{array} \text { for }-\infty<t<\infty\right.\)

   

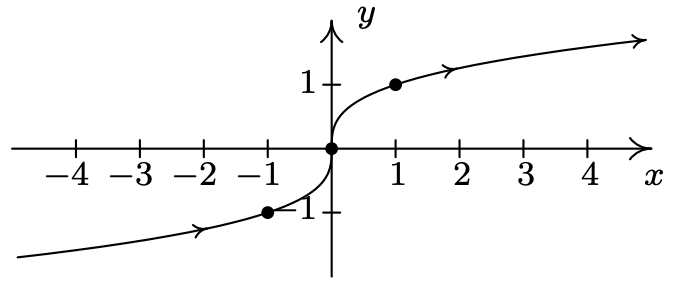
8. \(\left\{\begin{array}{l} x=t^{3} \\ y=t \end{array} \quad \text { for }-\infty<t<\infty\right.\)

   

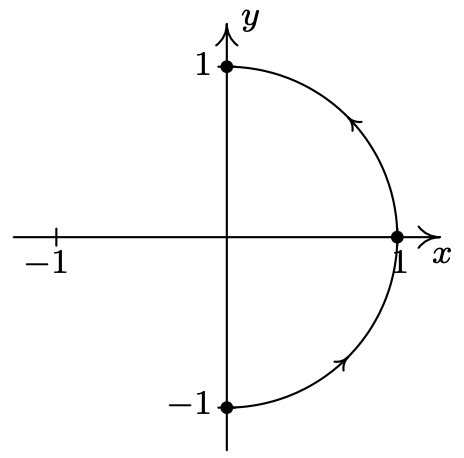
9. \(\left\{\begin{array}{l} x=\cos (t) \\ y=\sin (t) \end{array} \text { for }-\frac{\pi}{2} \leq t \leq \frac{\pi}{2}\right.\)

   

10. \(\left\{\begin{array}{l} x=3 \cos (t) \\ y=3 \sin (t) \end{array} \text { for } 0 \leq t \leq \pi\right.\)

    

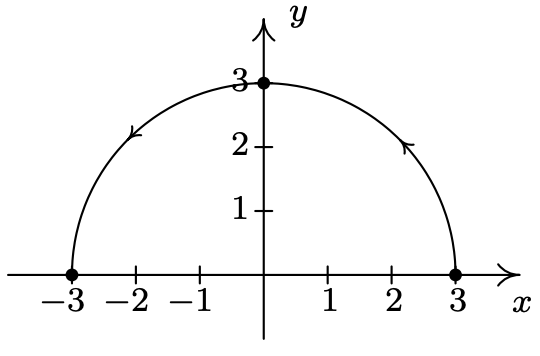
11. \(\left\{\begin{array}{l} x=-1+3 \cos (t) \\ y=4 \sin (t) \end{array} \quad \text { for } 0 \leq t \leq 2 \pi\right.\)

    

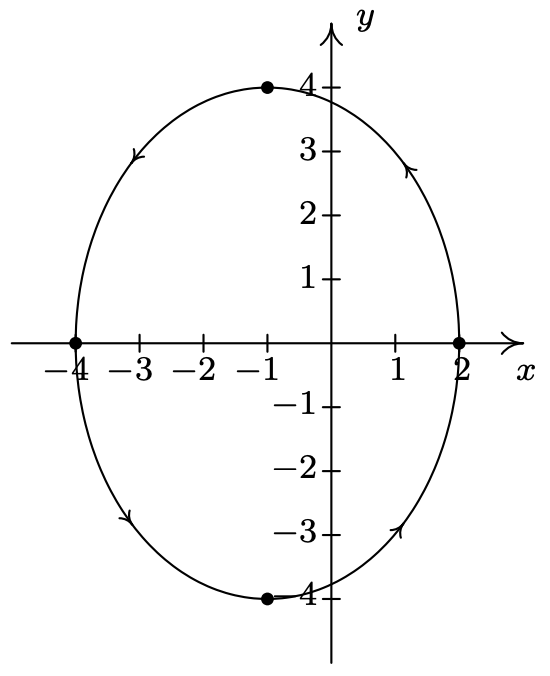
12. \(\left\{\begin{array}{l} x=3 \cos (t) \\ y=2 \sin (t)+1 \end{array} \text { for } \frac{\pi}{2} \leq t \leq 2 \pi\right.\)

    

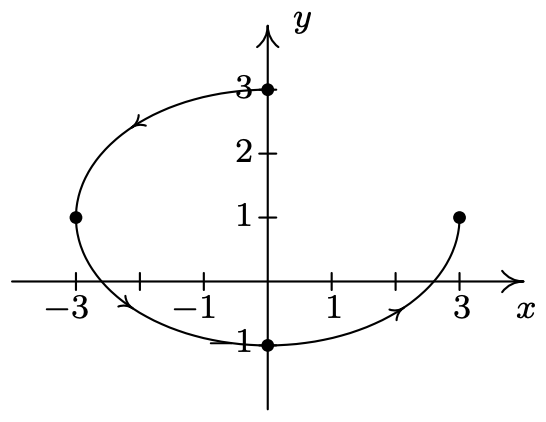
13. \(\left\{\begin{array}{l} x=2 \cos (t) \\ y=\sec (t) \end{array} \text { for } 0 \leq t<\frac{\pi}{2}\right.\)

    

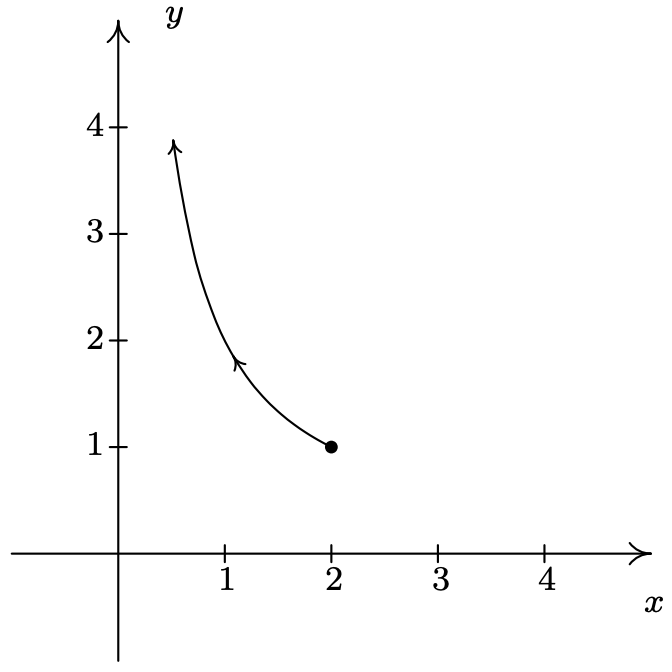
14. \(\left\{\begin{array}{l} x=2 \tan (t) \\ y=\cot (t) \end{array} \text { for } 0<t<\frac{\pi}{2}\right.\)

    

15. \(\left\{\begin{array}{l} x=\sec (t) \\ y=\tan (t) \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.\)

    

16. \(\left\{\begin{array}{l} x=\sec (t) \\ y=\tan (t) \end{array} \text { for } \frac{\pi}{2}<t<\frac{3 \pi}{2}\right.\)

    

17. \(\left\{\begin{array}{l} x=\tan (t) \\ y=2 \sec (t) \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.\)

    

18. \(\left\{\begin{array}{l} x=\tan (t) \\ y=2 \sec (t) \end{array} \text { for } \frac{\pi}{2}<t<\frac{3 \pi}{2}\right.\)

    

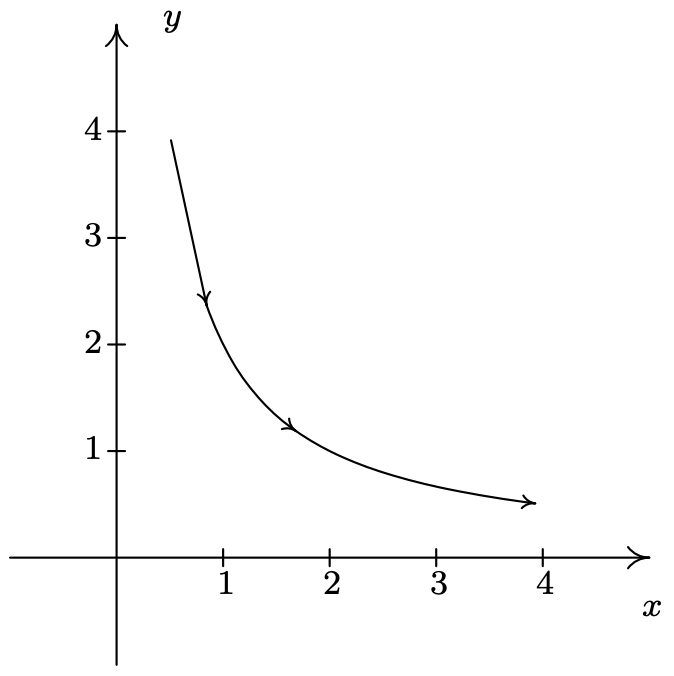
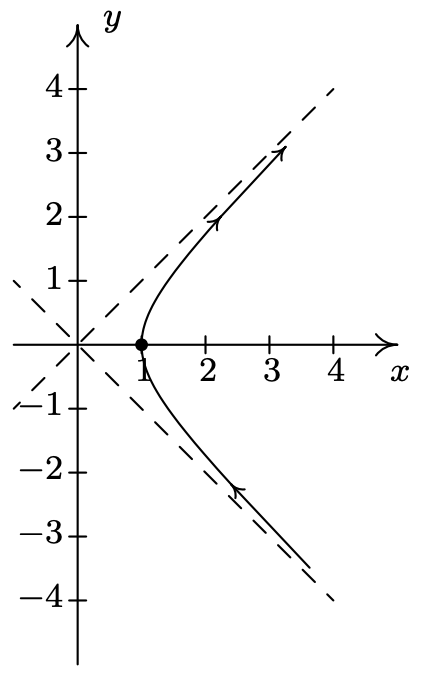
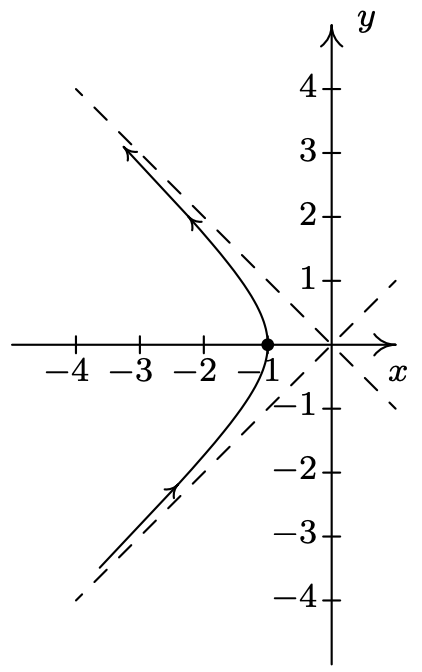
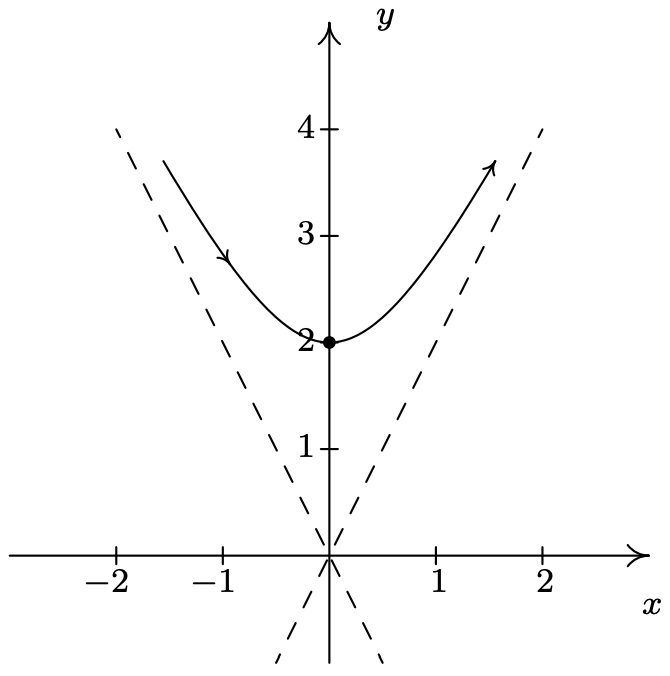
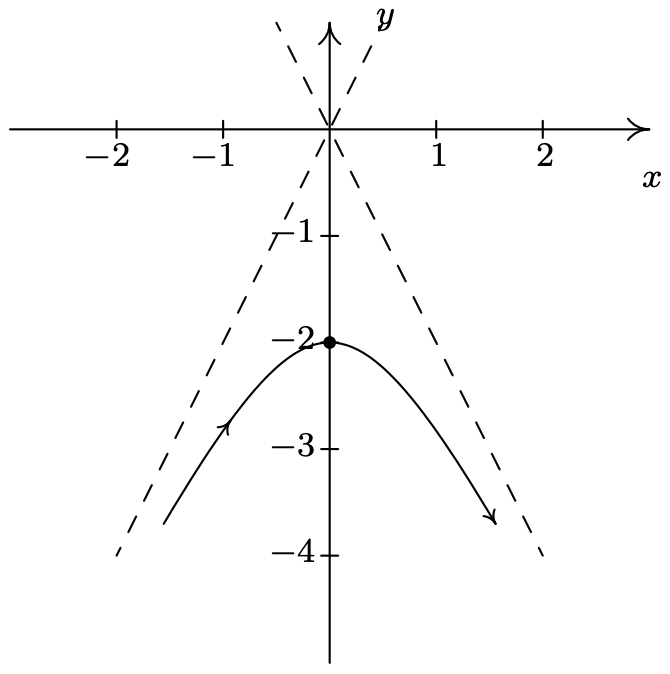
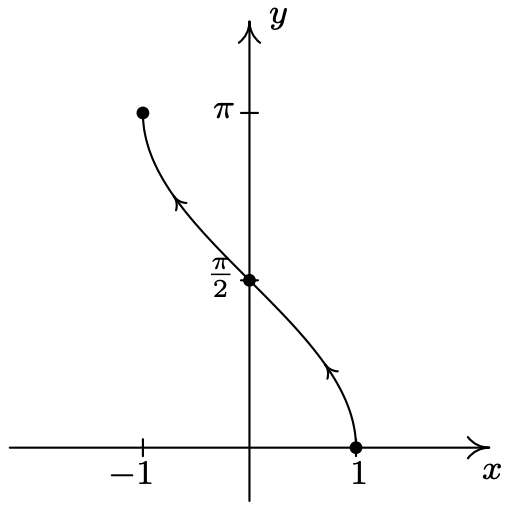
19. \(\left\{\begin{array}{l} x=\cos (t) \\ y=t \end{array} \text { for } 0<t<\pi\right.\)

    

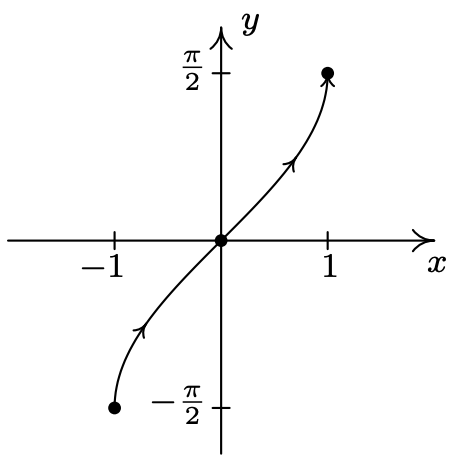
20. \(\left\{\begin{array}{l} x=\sin (t) \\ y=t \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.\)

    

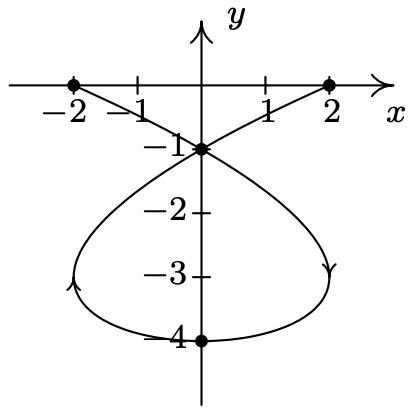
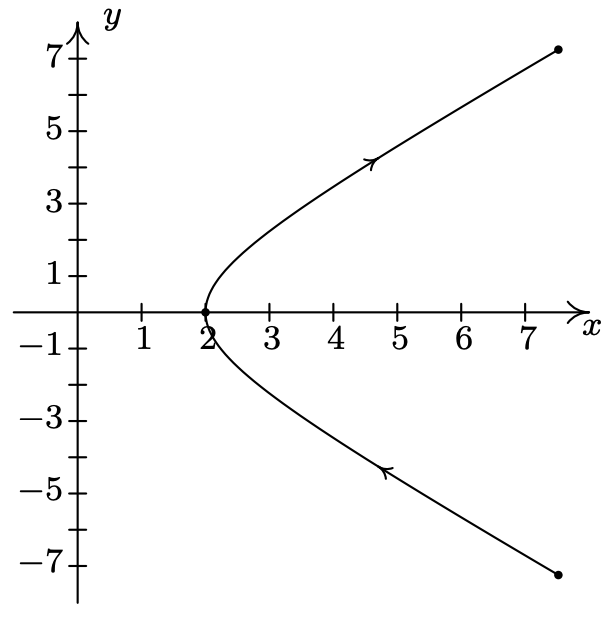
21. \(\left\{\begin{array}{l} x=t^{3}-3 t \\ y=t^{2}-4 \end{array} \text { for }-2 \leq t \leq 2\right.\)

    

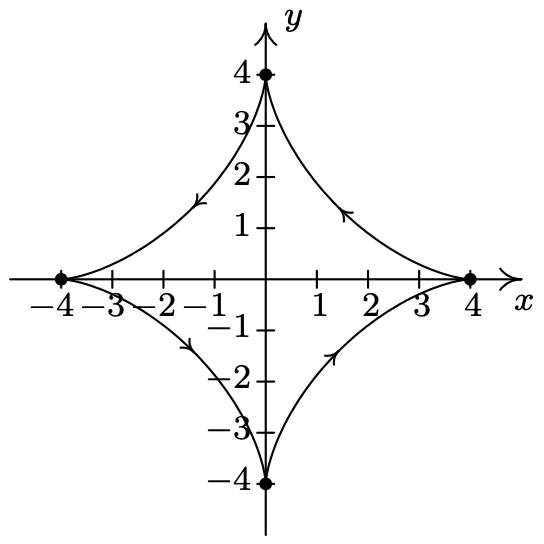
22. \(\left\{\begin{array}{l} x=4 \cos ^{3}(t) \\ y=4 \sin ^{3}(t) \end{array} \text { for } 0 \leq t \leq 2 \pi\right.\)

    

23. \(\left\{\begin{array}{l} x=e^{t}+e^{-t} \\ y=e^{t}-e^{-t} \end{array} \quad \text { for }-2 \leq t \leq 2\right.\)

    

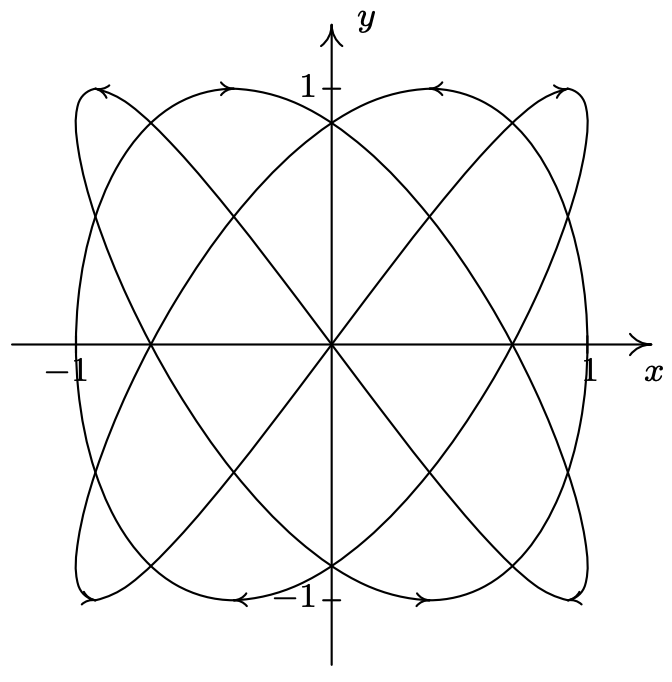
24. \(\left\{\begin{array}{l} x=\cos (3 t) \\ y=\sin (4 t) \end{array} \text { for } 0 \leq t \leq 2 \pi\right.\)

    

25. \(\left\{\begin{array}{l} x=3-5 t \\ y=-5+7 t \end{array} \text { for } 0 \leq t \leq 1\right.\)
26. \(\left\{\begin{array}{l} x=5 t-2 \\ y=-1-3 t \end{array} \text { for } 0 \leq t \leq 1\right.\)
27. \(\left\{\begin{array}{l} x=t \\ y=4-t^{2} \end{array} \text { for }-2 \leq t \leq 2\right.\)
28. \(\left\{\begin{array}{l} x=t-2 \\ y=4 t-t^{2} \end{array} \text { for } 0 \leq t \leq 4\right.\)
29. \(\left\{\begin{array}{l} x=t^{2}-9 \\ y=t \end{array} \text { for }-2 \leq t \leq 3\right.\)
30. \(\left\{\begin{array}{l} x=t^{2}-6 t \\ y=3-t \end{array} \quad \text { for } 0 \leq t \leq 5\right.\)
31. \(\left\{\begin{array}{l} x=5 \cos (t) \\ y=5 \sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.\)
32. \(\left\{\begin{array}{l} x=1+2 \cos (t) \\ y=2 \sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.\)
33. \(\left\{\begin{array}{l} x=3 \cos (t) \\ y=3+3 \sin (t) \end{array} \quad \text { for } 0 \leq t<2 \pi\right.\)
34. \(\left\{\begin{array}{l} x=3 \cos (t) \\ y=3-3 \sin (t) \end{array} \quad \text { for } 0 \leq t<2 \pi\right.\)
35. \(\left\{\begin{array}{l} x=3+\sqrt{117} \cos (t) \\ y=-1+\sqrt{117} \sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.\)
36. \(\left\{\begin{array}{l} x=1+3 \cos (t) \\ y=\sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.\)
37. \(\left\{\begin{array}{l} x=2 \cos (t) \\ y=3 \sin (t)-3 \end{array} \quad \text { for } 0 \leq t<2 \pi\right.\)
38. \(\left\{\begin{array}{l} x=2 \cos \left(t-\frac{\pi}{2}\right)=2 \sin (t) \\ y=-3-3 \sin \left(t-\frac{\pi}{2}\right)=-3+3 \cos (t) \end{array} \quad \text { for } 0 \leq t<2 \pi\right.\)
39. \(\{x(t), y(t) \text { where: }\)\[x(t)=\left\{\begin{array}{rl} 3 t, & 0 \leq t \leq 1 \\ 6-3 t, & 1 \leq t \leq 2 \\ 0, & 2 \leq t \leq 3 \end{array} \quad y(t)=\left\{\begin{aligned} 0, & 0 \leq t \leq 1 \\ 4 t-4, & 1 \leq t \leq 2 \\ 12-4 t, & 2 \leq t \leq 3 \end{aligned}\right.\right.\nonumber\]
40. Las ecuaciones paramétricas para la inversa son\(\left\{\begin{array}{l} x=t^{3}+3 t-4 \\ y=t \end{array} \text { for }-\infty<t<\infty\right.\)
41. \(r=6 \cos (2 \theta)\)se traduce en\(\left\{\begin{array}{l} x=6 \cos (2 \theta) \cos (\theta) \\ y=6 \cos (2 \theta) \sin (\theta) \end{array} \text { for } 0 \leq \theta<2 \pi\right.\)
42. Las ecuaciones paramétricas que describen la ubicación de los pasajeros en el London Eye son\[\left\{\begin{array}{l} x=67.5 \cos \left(\frac{\pi}{15} t-\frac{\pi}{2}\right)=67.5 \sin \left(\frac{\pi}{15} t\right) \\ y=67.5 \sin \left(\frac{\pi}{15} t-\frac{\pi}{2}\right)+67.5=67.5-67.5 \cos \left(\frac{\pi}{15} t\right) \end{array} \text { for }-\infty<t<\infty\right.\nonumber\]
43. Las ecuaciones paramétricas para el lanzamiento de martillo son\(\left\{\begin{array}{l} x=33 \cos \left(42^{\circ}\right) t \\ y=-16 t^{2}+33 \sin \left(42^{\circ}\right) t+6 \end{array}\right.\) para\(t \geq 0\). Para encontrar cuando el martillo golpea el suelo, resolvemos\(y(t)=0\) y obtenemos\(t \approx-0.23\) o 1.61. Ya que\(t \geq 0\), el martillo golpea el suelo después de aproximadamente\(t = 1.61\) segundos después de que fuera lanzado al aire. Para saber qué tan lejos golpea el martillo en el suelo, encontramos\(x(1.61) \approx 39.48\) pies de donde fue arrojado al aire.
44. Resolvemos\(y=\frac{v_{0}^{2} \sin ^{2}(\theta)}{2 g}+s_{0}=\frac{v_{0}^{2} \sin ^{2}\left(85^{\circ}\right)}{2(32)}+5=31.5\) para conseguir\(v_{0}=\pm 41.34\). La velocidad inicial de la gavilla fue de aproximadamente 41.34 pies por segundo.

---

Referencia

¹ Anotar el uso del artículo indefinido 'a'. Como veremos, hay infinitamente muchas representaciones paramétricas diferentes para cualquier curva dada.

² Aquí, el error llega al punto\(Q\) en dos momentos diferentes. Si bien esto no contradice nuestra afirmación de que\(f(t)\) y\(g(t)\) son funciones de\(t\), demuestra que ni\(f\) ni\(g\) puede ser uno a uno. (Piense en esto antes de seguir leyendo.)

³ Tendremos un ejemplo en breve donde no importa cómo restrinjamos x e y, nunca podremos describir con precisión la curva una vez que hayamos eliminado el parámetro.

⁴ Deberías revisar la Sección 1.6.1 si has olvidado lo que significan 'creciente', 'decreciente' y 'mínimo relativo'.

⁵ Se alienta al lector a revisar las Secciones 6.1 y 6.2 según sea necesario.

⁶ Anote el círculo abierto en el origen. Consulte la solución a la parte 3 en el Ejemplo 1.2.1 en la página 22 y el Teorema 4.1 en la Sección 4.1 para una revisión de este concepto.

⁷ Siempre que hayas seguido la teoría de la función inversa, por supuesto.

⁸ Compara y contrasta esto con el Ejercicio 65 en la Sección 11.8.

⁹ cortesía de las Identidades Pares/Impar

¹⁰ cortesía de las Fórmulas de Suma/Diferencia

¹¹ Si reemplazamos\(x\) con\(\frac{x}{r}\) y\(y\) con\(\frac{y}{r}\) en la ecuación para el Círculo de Unidad\(x^{2}+y^{2}=1\), obtenemos\(\left(\frac{x}{r}\right)^{2}+\left(\frac{y}{r}\right)^{2}=1\) cuál reduce a\(x^{2}+y^{2}=r^{2}\). En el lenguaje de la Sección 1.7, estamos estirando la gráfica por un factor tanto\(r\) en las direcciones\(x\) - como en\(y\) -direcciones. De ahí que multiplicamos las\(y\) coordenadas\(x\) - y -de los puntos en la gráfica por\(r\).

¹² ¿Esto le parece familiar? Ver Ejemplo 11.1.1 en la Sección 11.1.

¹³ Ver página 959 en la Sección 11.5.

¹⁴ Nuevamente, véase la página 959 en la Sección 11.5.

¹⁵ Se necesita una buena mezcla de vectores y Cálculo para derivar esto.

¹⁶ Ya lo hemos visto antes. Es el ángulo de elevación que se definió en la página 753.