1.2: Dominio y Rango

Uno de nuestros principales objetivos en matemáticas es modelar el mundo real con funciones matemáticas. Al hacerlo, es importante tener en cuenta las limitaciones de esos modelos que creamos.

Esta tabla muestra una relación entre la circunferencia y la altura de un árbol a medida que crece.

Circunferencia,\(c\)	1.7	2.5	5.5	8.2	13.7
Altura,\(h\)	24.5	31	45.2	54.6	92.1

Si bien existe una fuerte relación entre ambos, sin duda sería ridículo hablar de un árbol con una circunferencia de -3 pies, o una altura de 3000 pies. Cuando identificamos limitaciones en las entradas y salidas de una función, estamos determinando el dominio y el rango de la función.

Definiciones: Dominio y Rango

• Dominio: El conjunto de posibles valores de entrada a una función
• Rango: El conjunto de posibles valores de salida de una función

Ejemplo\(\PageIndex{1}\)

Usando la tabla de árbol anterior, determine un dominio y rango razonables.

Solución

Podríamos combinar los datos aportados con nuestras propias experiencias y razón para aproximar el dominio y rango de la función\(h = f(c)\). Para el dominio, posibles valores para la circunferencia de entrada\(c\), no tiene sentido tener valores negativos, entonces\(c > 0\). Podríamos hacer una conjetura educada a un valor máximo razonable, o buscar que la circunferencia máxima medida sea de aproximadamente 119 pies. Con esta información, diríamos que un dominio razonable es\(0< c \le 119\) pies.

De manera similar para el rango, no tiene sentido tener alturas negativas, y la altura máxima de un árbol se podría mirar hacia arriba para ser 379 pies, por lo que un rango razonable son\(0 < h \le 379\) pies.

Ejemplo\(\PageIndex{2}\)

Al enviar una carta a través del Servicio Postal de Estados Unidos, el precio depende del peso de la carta (https://pe.usps.com/text/dmm300/Notice123.htm, recuperado el 6 de agosto de 2018), tal y como se muestra en la siguiente tabla. Determinar el dominio y el rango.

Tabla: Letras

Peso no superior	Precio
1 onza	$0.50
2 onzas	$0.71
3 onzas	$0.92
3.5 onzas	$1.13

Supongamos que anotamos Peso por\(w\) y Precio por\(p\), y configuramos una función llamada\(P\), donde Price,\(p\) es una función de Peso,\(w. p = P(w).\)

Dado que los pesos aceptables son 3.5 onzas o menos, y los pesos negativos no tienen sentido, el dominio sería\(0< w \le 3.5\). Técnicamente se podría incluir 0 en el dominio, pero lógicamente significaría que no estamos mandando nada por correo, así que no está de más dejarlo fuera.

Dado que los precios posibles son de un conjunto limitado de valores, solo podemos definir el rango de esta función enumerando los valores posibles. El rango es\(p\) = $0.50, $0.71, $0.92, o $1.13.

Pruébalo ahora

La población de un pequeño pueblo en el año 1960 era de 100 personas. Desde entonces la población ha crecido a 1400 personas reportadas durante el censo de 2010. Elija variables descriptivas para su entrada y salida y use notación de intervalos para escribir el dominio y el rango.

Contestar

Dominio;\(y =\) años [1960, 2010]

Rango,\(p =\) población, [100, 1400]

Notación

En los ejemplos anteriores, se utilizaron desigualdades para describir el dominio y el rango de las funciones. Esta es una forma de describir intervalos de valores de entrada y salida, pero no es la única manera. Tomemos un momento para discutir la notación para dominio y rango.

El uso de desigualdades\(0 < c \le 163\), tales como\(0 < w \le 3.5\),, e\(0 < h \le 379\) implica que estamos interesados en todos los valores entre los valores bajos y altos, incluyendo los valores altos en estos ejemplos.

Sin embargo, ocasionalmente nos interesa una lista específica de números como el rango para el precio para enviar cartas,\(p\) = $0.44, $0.61, $0.78, o $0.95. Estos números representan un conjunto de valores específicos: {0.44, 0.61, 0.78, 0.95}

Representar valores como un conjunto, o dar instrucciones sobre cómo se construye un conjunto, nos lleva a otro tipo de notación para describir el dominio y el rango.

Supongamos que queremos describir los valores para una variable x que son 10 o mayores, pero menores que 30. En desigualdades, escribiríamos\(10 \le x < 30\).

Al describir dominios y rangos, a veces extendemos esto a la notación set-builder, que se vería así:\(\{x\ |\ 10 \le x < 30\}\). Los corchetes {} se leen como “el conjunto de”, y la barra vertical se lee como “tal que”, así que en conjunto leeríamos\(\{x\ |\ 10 \le x < 30\}\) como “el conjunto de x -valores tales que 10 es menor o igual a\(x\) y\(x\) es menor que 30”.

Al describir rangos en notación set-builder, podríamos escribir de manera similar algo así como\(\{f(x)\ |\ 0 < f(x) < 30\}\), o si la salida tuviera su propia variable, podríamos usarla. Entonces, para nuestro ejemplo de altura de árbol anterior, podríamos escribir para el rango\(\{h\ |\ 0 < h \le 379\}\). En la notación set-builder, si un dominio o rango no está limitado, podríamos escribir {\(t\)|\(t\) es un número real}, o\(\{t\ |\ t \in \mathbb{R}\}\), leer como “el conjunto de t -valores tal que\(t\) es un elemento del conjunto de números reales.

Una alternativa más compacta a la notación set-builder es la notación de intervalos, en la que los intervalos de valores son referidos por los valores inicial y final. Los paréntesis curvos se utilizan para “estrictamente menos que” y los corchetes se usan para “menos que o igual a”. Como infinito no es un número, no podemos incluirlo en el intervalo, por lo que siempre usamos paréntesis curvos con\(\infty\) y -\(\infty\). La siguiente tabla le ayudará a ver cómo las desigualdades corresponden a la notación set-builder y la notación de intervalo:

Desigualdad	Notación del constructor de conjuntos	Notación de intervalos
\(5 < h \le 10\)	\(\{h\ |\ 5 < h \le 10\}\)	(5, 10]
\(5 \le h < 10\)	\(\{h\ |\ 5 \le h < 10\}\)	[5, 10)
\(5 < h < 10\)	\(\{h\ |\ 5 < h < 10\}\)	(5, 10)
\(h < 10\)	\(\{h\ |\ h < 10\}\)	\((-\infty ,10)\)
\(h \ge 10\)	\(\{h\ |\ h \ge 10\}\)	\([10, \infty )\)
todos los números reales	\(\{h\ |\ h \in \mathbb{R}\}\)	\((-\infty, \infty )\)

Para combinar dos intervalos juntos, usando desigualdades o notación set-builder podemos usar la palabra “or”. En la notación de intervalos, usamos el símbolo de unión\(\cup\),, para combinar dos intervalos desconectados juntos.

Ejemplo\(\PageIndex{3}\)

Describa los intervalos de valores mostrados en el gráfico de líneas a continuación utilizando el generador de conjuntos y las notaciones de intervalos.

Para describir los valores,\(x\), que se encuentran en los intervalos mostrados anteriormente diríamos, “x es un número real mayor o igual a 1 y menor o igual a 3, o un número real mayor que 5”.

• Como desigualdad es:\[1 \le x \le 3\quad \text{or} \quad x > 5 \nonumber\]
• En notación de constructor de conjuntos:\[\{x|1 \le x \le 3 \quad \text{or} \quad x > 5\} \nonumber\]
• En notación de intervalos:\[[1,3] \cup (5, \infty ) \nonumber\]

Recuerde al escribir o leer notación de intervalo:

Usando un corchete [significa que el valor inicial está incluido en el conjunto

Usar un paréntesis (significa que el valor inicial no está incluido en el conjunto

Pruébalo ahora

Dado el siguiente intervalo, escriba su significado en palabras, notación de generador de conjuntos y notación de intervalo.

Contestar

a. Valores menores o iguales a -2, o valores que son mayores o iguales a -1 y menores que 3

b.\(\{x\ |\ x \le -2\ or \ -1 \le x < 3\}\)

c.\((-\infty, -2] \cup [-1, 3)\)

Dominio y Rango a partir de Gráficos

También podemos hablar de dominio y rango a partir de gráficas. Dado que domain se refiere al conjunto de posibles valores de entrada, el dominio de una gráfica consiste en todos los valores de entrada mostrados en la gráfica. Recuerde que los valores de entrada casi siempre se muestran a lo largo del eje horizontal de la gráfica. Así mismo, dado que range es el conjunto de posibles valores de salida, el rango de una gráfica podemos ver a partir de los posibles valores a lo largo del eje vertical de la gráfica.

Tenga cuidado — si la gráfica continúa más allá de la ventana en la que podemos ver la gráfica, el dominio y el rango podrían ser mayores que los valores que podemos ver.

Ejemplo\(\PageIndex{4}\)

Determine el dominio y el rango de la gráfica a continuación.

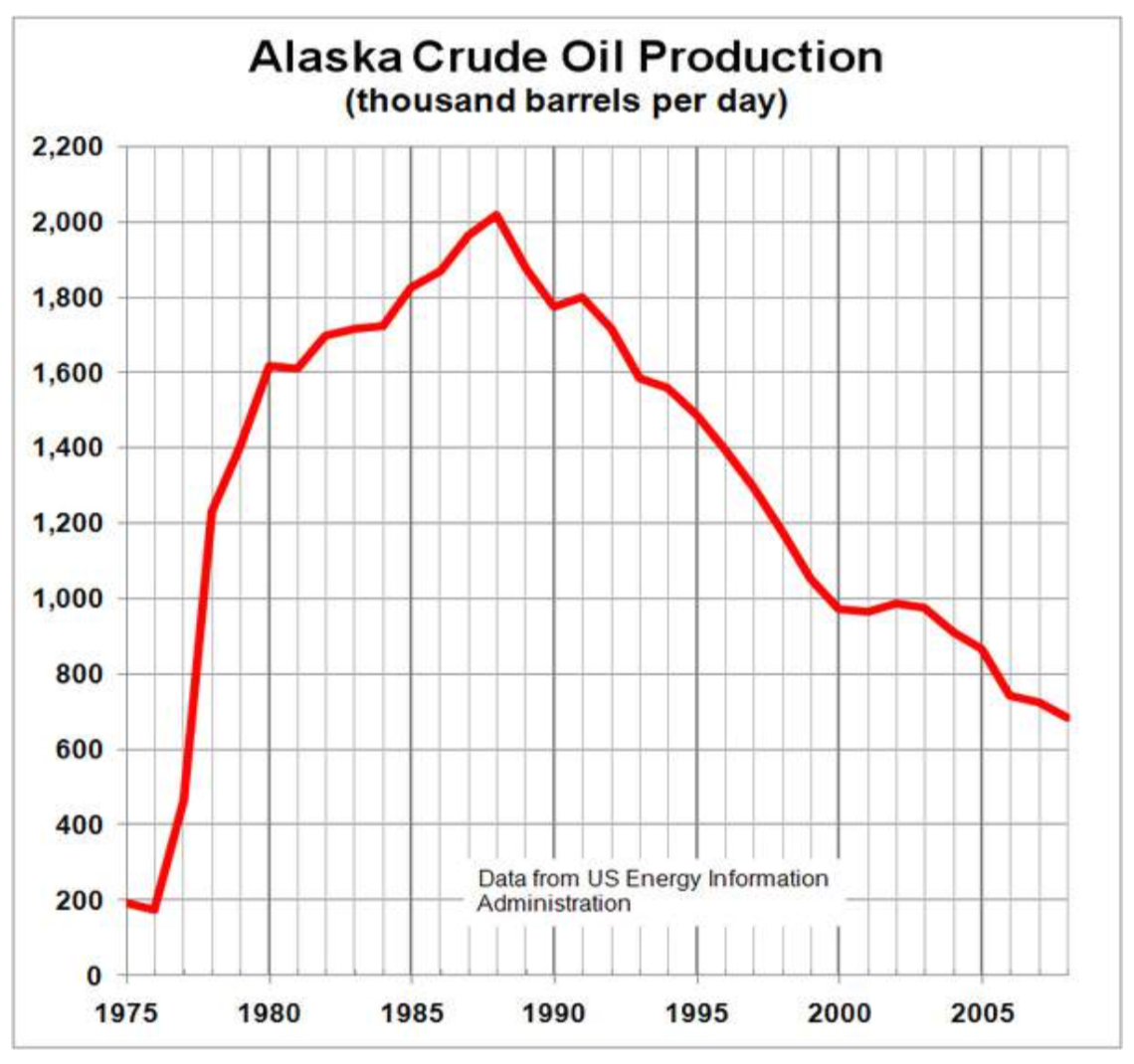
Solución

En la gráfica anterior (http://commons.wikimedia.org/wiki/Fi...Production.PNG, CC-BY-SA, 19 de julio de 2010), la cantidad de entrada a lo largo del eje horizontal parece ser “año”, que podríamos anotar con la variable y. La producción es de “miles de barriles de petróleo por día”, que podríamos anotar con la variable b, para barriles. El gráfico probablemente continuaría hacia la izquierda y hacia la derecha más allá de lo que se muestra, pero con base en la porción de la gráfica que se nos muestra, podemos determinar el dominio es\(1975\le y\le 2008\), y el rango es aproximadamente\(180\le b\le 2010\).

En notación de intervalos, el dominio sería [1975, 2008] y el rango sería de aproximadamente [180, 2010]. Para el rango, tenemos que aproximar las salidas más pequeñas y mayores ya que no caen exactamente en las líneas de la cuadrícula.

Recuerda que, como en el ejemplo anterior, x e y no son siempre las variables de entrada y salida. El uso de variables descriptivas es una herramienta importante para recordar el contexto del problema.

Pruébalo ahora

Dada la gráfica a continuación, escriba el dominio y el rango en notación de intervalos

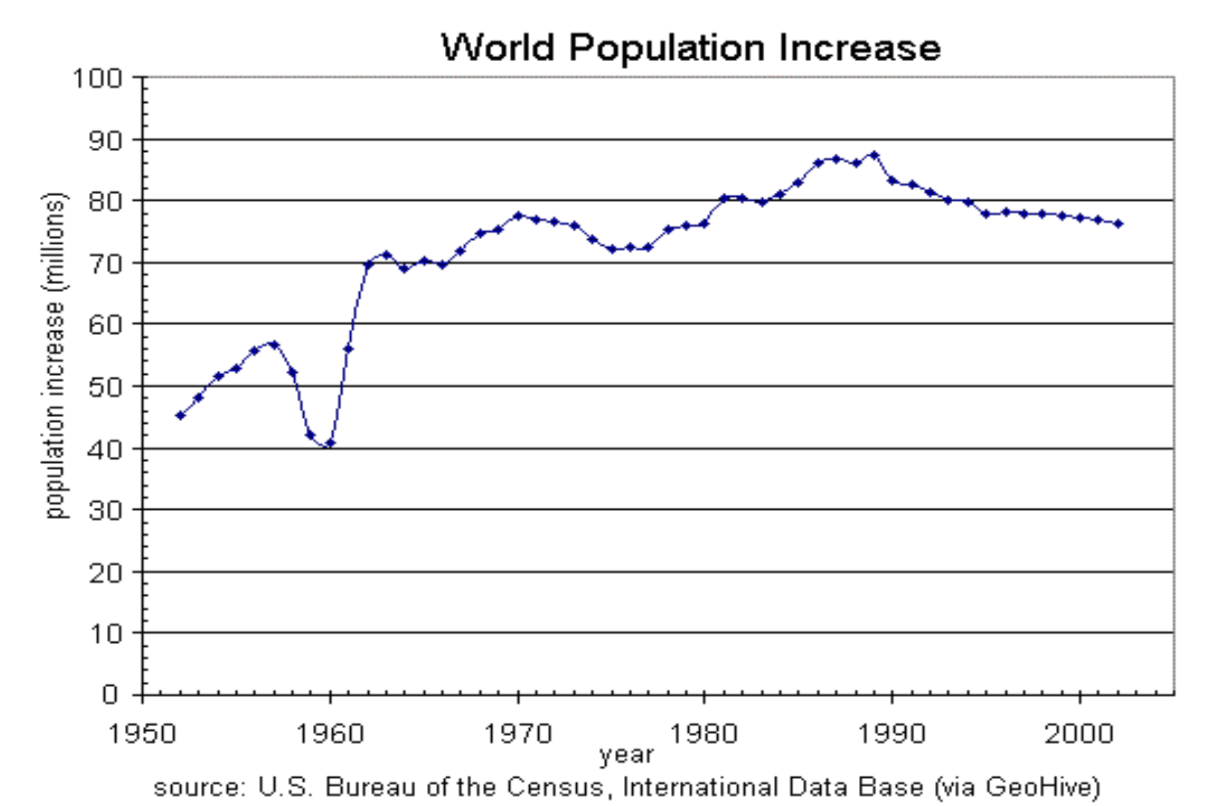
Contestar

Dominio;\(y =\) años, [1952, 2002]; Rango,\(p =\) población en millones, [40, 88]

Dominios y rangos de las funciones del kit de herramientas

Ahora volveremos a nuestro conjunto de funciones del kit de herramientas para anotar el dominio y el rango de cada uno.

Función constante:\(f(x)=c\)

• El dominio aquí no está restringido;\(x\) puede ser cualquier cosa. Cuando este es el caso decimos que el dominio es todo números reales. Las salidas están limitadas al valor constante de la función.
• Dominio:\((-\infty ,\infty )\)
• Rango: [\(c\)]
• Como solo hay un valor de salida, lo enumeramos por sí mismo entre corchetes.

Función de identidad:\(f(x)=x\)

• Dominio:\((-\infty ,\infty )\)
• Rango:\((-\infty ,\infty )\)

Función cuadrática:\(f(x)=x^{2}\)

• Dominio:\((-\infty , \infty )\)
• Rango:\([0, \infty )\)
• Multiplicar un número negativo o positivo por sí solo puede producir una salida positiva.

Función cúbica:\(f(x)=x^{3}\)

• Dominio:\((-\infty ,\infty )\)
• Rango:\((-\infty ,\infty )\)

Recíproco:\(f(x)=\dfrac{1}{x}\)

• Dominio:\((-\infty , 0) \cup (0, \infty )\)
• Rango:\((-\infty , 0) \cup (0, \infty )\)
• No podemos dividir por 0 así que debemos excluir 0 del dominio.
• Una división por cualquier valor nunca puede ser 0, por lo que el rango no incluirá 0.

Recíproco al cuadrado:\(f(x)=\dfrac{1}{x^{2} }\)

• Dominio:\((-\infty ,0) \cup (0,\infty)\)
• Rango:\((0,\infty )\)
• No podemos dividir por 0 así que debemos excluir 0 del dominio.

Raíz cúbica:\(f(x)=\sqrt[3]{x}\)

• Dominio:\((-\infty, \infty )\)
• Rango:\((-\infty, \infty )\)

Raíz cuadrada:\(f(x)=\sqrt[2]{x}\), comúnmente solo escrito como,\(f(x)=\sqrt{x}\)

• Dominio:\([0,\infty )\)
• Rango:\([0,\infty )\)
• Al tratar con el conjunto de números reales no podemos tomar la raíz cuadrada de un número negativo por lo que el dominio se limita a 0 o mayor.

Función de valor absoluto:\(f(x) = |x|\)

• Dominio:\((-\infty, \infty)\)
• Rango:\([0, \infty)\)
• Dado que el valor absoluto se define como una distancia desde 0, la salida solo puede ser mayor o igual a 0.

Ejemplo\(\PageIndex{5}\)

Encuentra el dominio de cada función:

1. \(f(x)=2\sqrt{x+4}\)
2. \(g(x)=\dfrac{3}{6-3x}\)

Solución

a) Como no podemos tomar la raíz cuadrada de un número negativo, necesitamos que el interior de la raíz cuadrada sea no negativo.

\(x + 4 \ge 0\)cuando\(x \ge -4\).

El dominio de\(f(x)\) es\([-4, \infty)\).

b) No podemos dividir por cero, así que necesitamos que el denominador sea distinto de cero.

\(6 - 3x = 0\)cuando x = 2, por lo que debemos excluir 2 del dominio.

El dominio de g (x) es\((-\infty , 2) \cup (2, \infty)\).

Funciones por piezas

En las funciones del kit de herramientas introdujimos la función de valor absoluto\(f(x)=\left|x\right|\).

Con un dominio de todos los números reales y un rango de valores mayor o igual a 0, el valor absoluto puede definirse como la magnitud o módulo de un número, un valor de número real independientemente del signo, el tamaño del número o la distancia desde 0 en la línea numérica. Todas estas definiciones requieren que la salida sea mayor o igual a 0.

Si entramos 0, o un valor positivo, la salida no cambia

\(f(x) = x\)si\(x \ge 0\)

Si se ingresa un valor negativo el signo debe cambiar de negativo a positivo.

\(f(x) = -x\)si\(x < 0\), ya que multiplicar un valor negativo por -1 lo hace positivo.

Dado que esto requiere dos procesos o piezas diferentes, la función de valor absoluto a menudo se llama la función definida por partes más básica.

Definición: Función por partes

Una función por partes es una función en la que la fórmula utilizada depende del dominio en el que se encuentra la entrada. Notamos esta idea como:

\[f(x) = \begin{cases} \text{formula 1 if domain to use formula 1} \\ \text{formula 2 if domain to use formula 2} \\ \text{formula 3 if domain to use formula 3} \end{cases}\nonumber \]

Ejemplo\(\PageIndex{6}\)

Un museo cobra $5 por persona por una visita guiada con un grupo de 1 a 9 personas, o una tarifa fija de $50 para 10 o más personas en el grupo. Establecer una función que relacione el número de personas,\(n\), con el costo,\(C\).

Solución

Para configurar esta función, se necesitarían dos fórmulas diferentes. C = 5 n funcionaría para n valores menores de 10, y C = 50 funcionaría para valores de n diez o mayores. Notando esto:

\[C(n) = \begin{cases} 5n & if & 0 < n < 10 \\ 50 & if & n \ge 10 \end{cases}\nonumber \]

Ejemplo\(\PageIndex{7}\)

Una compañía de telefonía celular utiliza la siguiente función para determinar el costo, C, en dólares por g gigabytes de transferencia de datos.

\[C(g)=\left\{\begin{array}{ccc} {25} & {if} & {0<g<2} \\ {25+10(g-2)} & {if} & {g\ge 2} \end{array}\right.\nonumber \]

Encuentre el costo de usar 1.5 gigabytes de datos, y el costo de usar 4 gigabytes de datos.

Solución

Para encontrar el costo de usar 1.5 gigabytes de datos,\(C(1.5)\), primero miramos para ver en qué parte de dominio cae nuestra entrada. Ya que 1.5 es menor que 2, usamos la primera fórmula, dando\(C(1.5)\) = $25.

El encontrar el costo de usar 4 gigabytes de datos,\(C(4)\), vemos que nuestra entrada de 4 es mayor que 2, por lo que usaremos la segunda fórmula. \(C(4)\)= 25 + 10 (4 - 2) = $45.

Ejemplo\(\PageIndex{8}\)

Croquis de una gráfica de la función\(f(x)=\left\{\begin{array}{ccc} {x^{2} } & {if} & {x\le 1} \\ {3} & {if} & {1<x\le 2} \\ {6-x} & {if} & {x>2} \end{array}\right.\)

Solución

Las dos primeras funciones componentes son de nuestra biblioteca de funciones de Toolkit, por lo que conocemos sus formas. Podemos imaginar graficar cada función, luego limitando la gráfica al dominio indicado. En los puntos finales del dominio, colocamos círculos abiertos para indicar dónde no se incluye el punto final, debido a una desigualdad rigurosamente menor que, y un círculo cerrado donde se incluye el punto final, debido a una desigualdad menor o igual a la desigualdad.

Para la tercera función, debes reconocer esto como una ecuación lineal de tus cursos anteriores. Si recuerdas cómo graficar una línea usando pendiente e intercepción, puedes hacerlo. De lo contrario, podríamos calcular un par de valores, trazar puntos y conectarlos con una línea.

• En\(x = 2\),\(f(2) = 6 - 2 = 4\). Aquí colocamos un círculo abierto.
• En\(x = 3\),\(f(3) = 6 - 3 = 3\). Conecta estos puntos con una línea.

Ahora que tenemos cada pieza individualmente, las combinamos en la misma gráfica:

Pruébalo ahora

En Pierce College durante el ciclo escolar 2009-2010 las tasas de matrícula para residentes en el estado fueron de $89.50 por crédito para los primeros 10 créditos, $33 por crédito para créditos 11-18, y para mayores de 18 créditos la tasa es de $73 por crédito (www.pierce.ctc.edu/dist/tuit... ition_rate.pdf, recuperado el 6 de agosto de 2010). Escribir una función definida por partes para la matrícula total,\(T\), en Pierce College durante 2009-2010 en función del número de créditos tomados,\(c\). Asegúrese de considerar un dominio y rango razonables

Contestar

\(T(c) = \begin{cases} 89.5c & if & c \le 10 \\ 895 + 33(c - 10) & if & 10 < c \le 18 \\ 1159 + 73(c - 18) & if & c > 18 \end{cases}\)Matrícula\(T\),, en función de los créditos,\(c\).

El dominio razonable debe ser números enteros 0 a (las respuestas pueden variar), por ejemplo [0, 23]

El rango razonable debe ser $0 — (las respuestas pueden variar), por ejemplo [0,1524]

Temas Importantes de esta Sección

• Definición de dominio
• Definición de rango
• Desigualdades
• Notación de intervalos
• Notación de constructor de conjuntos
• Dominio y Rango a partir de gráficas
• Dominio y rango de funciones del kit de herramientas
• Funciones definidas por partes