1.3: Tasas de Cambio y Comportamiento de las Gráficas

Dado que las funciones representan cómo varía una cantidad de salida con una cantidad de entrada, es natural preguntar sobre la velocidad a la que cambian los valores de la función. Por ejemplo, la función\(C(t)\) a continuación da el costo promedio, en dólares, de un galón de gasolina\(t\) años después del 2000.

\(t\)	2	3	4	5	6	7	8	9
\(C(t)\)	1.47	1.69	1.94	2.30	2.51	2.64	3.01	2.14

Si nos interesara cómo habían cambiado los precios de la gasolina entre 2002 y 2009, podríamos calcular que el costo por galón había aumentado de $1.47 a $2.14, un incremento de $0.67. Si bien esto es interesante, podría ser más útil observar cuánto cambió el precio por año. Probablemente estés notando que el precio no cambiaba la misma cantidad cada año, por lo que estaríamos encontrando la tasa promedio de cambio en un período de tiempo específico.

El precio de la gasolina aumentó 0.67 dólares de 2002 a 2009, a lo largo de 7 años, por un promedio de\(\dfrac{\$ 0.67}{7years} \approx 0.096\) dólares anuales. En promedio, el precio del gas aumentó alrededor de 9.6 centavos cada año.

Definición: Tasa de cambio

Una tasa de cambio describe cómo cambia la cantidad de salida en relación con la cantidad de entrada. Las unidades en una tasa de cambio son unidades de salida por unidades de entrada.

Algunos otros ejemplos de tasas de cambio serían cantidades como:

• Una población de ratas aumenta en 40 ratas por semana
• Un barista gana $9 por hora (dólares por hora)
• Un granjero planta 60.000 cebollas por acre
• Un auto puede conducir 27 millas por galón
• Una población de ballenas grises disminuye en 8 ballenas al año
• La cantidad de dinero en tu cuenta universitaria disminuye en $4,000 por trimestre

Definición: Tasa promedio de cambio

La tasa promedio de cambio entre dos valores de entrada es el cambio total de los valores de función (valores de salida) dividido por el cambio en los valores de entrada.

\[\text{Average rate of change} = \dfrac{\text{Change of Output}}{\text{Change of Input}} = \dfrac{\Delta y}{\Delta x} =\dfrac{y_{2} -y_{1} }{x_{2} -x_{1} }\]

Ejemplo\(\PageIndex{1}\)

Usando la función de costo de gas anterior, encuentre la tasa promedio de cambio entre 2007 y 2009.

Solución

De la tabla, en 2007 el costo del gas fue de $2.64. En 2009 el costo fue de $2.14.

El insumo (años) ha cambiado en 2. La salida ha cambiado en $2.14 - $2.64 = -0.50.

La tasa promedio de cambio es entonces\(\dfrac{-\$ 0.50}{2years}\) = -0.25 dólares anuales

Ejercicio\(\PageIndex{1}\)

Usando la misma función de costo de gas, encuentre la tasa promedio de cambio entre 2003 y 2008

Contestar

\(\dfrac{$3.01 - $1.69}{5\ years} = \dfrac{$1.32}{5\ years} = 0.264\)dólares al año.

Observe que en el último ejemplo el cambio de salida fue negativo ya que el valor de salida de la función había disminuido. Correspondientemente, la tasa promedio de cambio es negativa.

Ejemplo\(\PageIndex{2}\)

Dada la función que\(g(t)\) se muestra aquí, encuentra la tasa promedio de cambio en el intervalo [0, 3].

Solución

A t = 0, la gráfica muestra\(g(0) = 1\)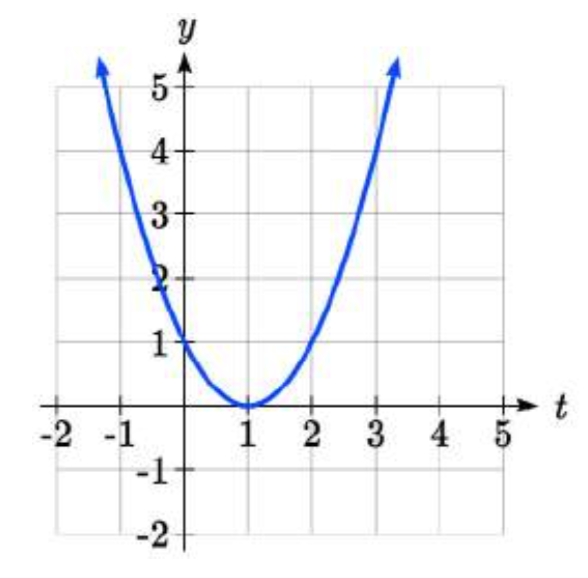

A t = 3, la gráfica muestra\(g(3) = 4\)

La salida ha cambiado en 3 mientras que la entrada ha cambiado en 3, dando una tasa promedio de cambio de:

\[\dfrac{4-1}{3-0} =\dfrac{3}{3} =1\nonumber \]

Ejemplo\(\PageIndex{3}\)

En un viaje por carretera, después de recoger a tu amigo que vive a 10 millas de distancia, decides registrar tu distancia de casa a lo largo del tiempo. Encuentra tu velocidad promedio durante las primeras 6 horas.

\(t\)(horas)	0	1	2	3	4	5	6	7
\(D(t)\)(millas)	10	55	90	153	214	240	292	300

Solución

Aquí, tu velocidad promedio es la tasa promedio de cambio.

Viajaste 282 millas en 6 horas, para una velocidad promedio de

\[\dfrac{292-10}{6-0} =\dfrac{282}{6}= 47\text{ miles per hour}\nonumber\]

Podemos declarar de manera más formal el cálculo de la tasa de cambio promedio utilizando la notación de funciones.

Definición: Tasa promedio de cambio usando la notación de funciones

Dada una función\(f(x)\), la tasa promedio de cambio en el intervalo [a, b] es

\[\text{Average rate of change} = \dfrac{\text{Change of Output}}{\text{Change of Input}} =\dfrac{f(b)-f(a)}{b-a} \label{avgratefunction}\]

Ejemplo\(\PageIndex{4}\)

Calcular la tasa promedio de cambio de\(f(x)=x^{2} -\dfrac{1}{x}\) en el intervalo [2, 4].

Solución

Podemos comenzar calculando los valores de la función en cada punto final del intervalo

\[f(2)=2^{2} -\dfrac{1}{2} =4-\dfrac{1}{2} =\dfrac{7}{2} \nonumber\]

\[f(4)=4^{2} -\dfrac{1}{4} =16-\dfrac{1}{4} =\dfrac{63}{4} \nonumber\]

Ahora calculando la tasa promedio de cambio

\[\text{Average rate of change} = \dfrac{f(4) - f(2)}{4 - 2} =\dfrac{\dfrac{63}{4} -\dfrac{7}{2} }{4-2} =\dfrac{\dfrac{49}{4} }{2} = \dfrac{49}{8} \nonumber\]

Ejercicio\(\PageIndex{2}\)

Encuentra la tasa promedio de cambio de\(f(x) = x - 2\sqrt{x}\) en el intervalo [1, 9].

Contestar

Tasa promedio de cambio =\(\dfrac{f(9) - f(1)}{9 - 1} = \dfrac{(9 - 2\sqrt{9}) - (1 - 2\sqrt{1})}{9 - 1} = \dfrac{(3) - (-1)}{9 - 1} = \dfrac{4}{8} = \dfrac{1}{2}\)

Ejemplo\(\PageIndex{5}\)

La fuerza magnética\(F\), medida en Newtons, entre dos imanes está relacionada con la distancia entre los imanes\(d\), en centímetros, por la fórmula\(F(d)=\dfrac{2}{d^{2} }\). Encuentra la tasa promedio de cambio de fuerza si la distancia entre los imanes se incrementa de 2 cm a 6 cm.

Solución

Estamos calculando la tasa promedio de cambio de\(F(d)=\dfrac{2}{d^{2} }\) en el intervalo [2, 6].

Tasa promedio de cambio =\(\dfrac{F(6) - F(2)}{6 - 2}\)

Evaluar la función

\[\dfrac{F(6)-F(2)}{6-2} =\nonumber \]

\[= \dfrac{\dfrac{2}{6^{2} } -\dfrac{2}{2^{2} } }{6-2}\nonumber \]Simplificando

\[= \dfrac{\dfrac{2}{36} -\dfrac{2}{4} }{4}\nonumber \]Combinando los términos del numerador

\[= \dfrac{\dfrac{-16}{36} }{4}\nonumber \]Simplificando aún más

\[= \dfrac{-1}{9}\nonumber \]Newtons por centímetro

Esto nos dice que la fuerza magnética disminuye, en promedio, en 1/9 Newtons por centímetro a lo largo de este intervalo.

Ejemplo\(\PageIndex{6}\)

Encuentra la tasa promedio de cambio de\(g(t)=t^{2} +3t+1\) en el intervalo\([0, a]\). Tu respuesta será una expresión que involucre a un.

Solución

Usando la fórmula de tasa de cambio promedio

\[\dfrac{g(a)-g(0)}{a-0}\nonumber\]

Evaluar la función

\[\dfrac{(a^{2} +3a+1)-(0^{2} +3(0)+1)}{a-0}\nonumber\]

Simplificando

\[\dfrac{a^{2} +3a+1-1}{a}\nonumber\]

Simplificar aún más y factorizar

\[\dfrac{a(a+3)}{a}\nonumber\]

Cancelación del factor común\(a\)

\[a+3\nonumber\]

Este resultado nos indica la tasa promedio de cambio entre t = 0 y cualquier otro punto t = a. Por ejemplo, en el intervalo [0, 5], la tasa promedio de cambio sería de 5+3 = 8.

Ejercicio\(\PageIndex{3}\)

Encuentra la tasa promedio de cambio de\(f(x)=x^{3} +2\) en el intervalo\([a,a+h]\).

Contestar

\[\dfrac{f(a + h) - f(a)}{(a + h) - a} = \dfrac{((a + h)^3 + 2) - (a^3 + 2)}{h} = \dfrac{a^3 + 3a^2h + 3ah^2 + h^3 + 2 - a^3 - 2}{h} = \dfrac{3a^2h + 3ah^2 + h^3}{h} = \dfrac{h(3a^2 + 3ah + h^2)}{h} = 3a^2 + 3ah + h^2\nonumber\]

Comportamiento gráfico de las funciones

Como parte de explorar cómo cambian las funciones, es interesante explorar el comportamiento gráfico de las funciones.

Definición: aumentar/disminuir

Una función aumenta en un intervalo si los valores de la función aumentan a medida que aumentan las entradas. Más formalmente, una función está aumentando si\(f(b) > f(a)\) para cualquiera de dos valores de entrada a y b en el intervalo con\(b > a\). La tasa promedio de cambio de una función creciente es positiva.

Una función disminuye en un intervalo si los valores de la función disminuyen a medida que aumentan las entradas. De manera más formal, una función está disminuyendo si\(f(b) < f(a)\) para dos valores de entrada cualesquiera a y b en el intervalo con\(b > a\). La tasa promedio de cambio de una función decreciente es negativa.

Ejemplo\(\PageIndex{7}\)

Dada la función\(p(t)\) graficada aquí, ¿en qué intervalos la función parece estar aumentando?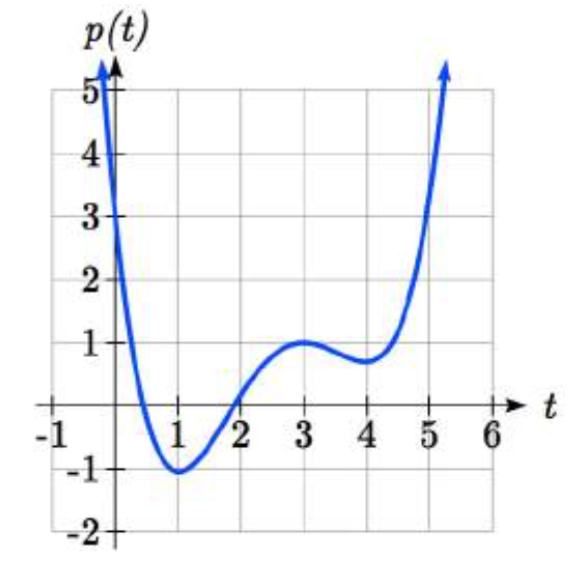

La función parece estar aumentando de\(t = 1\) a\(t = 3\), y de\(t = 4\) en adelante.

En notación de intervalos, diríamos que la función parece estar aumentando en el intervalo\((1, 3)\) y el intervalo\((4, \infty)\).

Solución

Agrega texto aquí.

Observe en el último ejemplo que usamos intervalos abiertos (intervalos que no incluyen los puntos finales) ya que la función no está aumentando ni disminuyendo a\(t =\) 1, 3 o 4.

Definición: Local Extrema

Un punto donde una función cambia de aumentar a disminuir se denomina máximo local.

Un punto donde una función cambia de disminuir a aumentar se denomina mínimo local.

En conjunto, los máximos y mínimos locales se denominan los extremos locales, o valores extremos locales, de la función.

Ejemplo\(\PageIndex{8}\)

Utilizando la función costo de la gasolina desde el inicio de la sección, encuentra un intervalo en el que la función parece estar disminuyendo. Estima cualquier extremo local usando la tabla.

\(t\)	2	3	4	5	6	7	8	9
\(C(t)\)	1.47	1.69	1.94	2.30	2.51	2.64	3.01	2.14

Parece que el costo del gas aumentó de\(t = 2\) a\(t = 8\). Parece que el costo del gas disminuyó de\(t = 8\) a\(t = 9\), por lo que la función parece estar disminuyendo en el intervalo (8, 9).

Dado que la función parece cambiar de aumentar a disminuir en\(t = 8\), hay máximo local en\(t = 8\).

Ejemplo\(\PageIndex{9}\)

Utilice una gráfica para estimar los extremos locales de la función\(f(x)=\dfrac{2}{x} +\dfrac{x}{3}\). Utilízalos para determinar los intervalos en los que la función está aumentando.

Solución

Usando la tecnología para graficar la función, parece que hay un mínimo local en algún lugar entre\(x = 2\) y\(x = 3\), y un máximo local simétrico en algún lugar entre\(x = -3\) y\(x = -2\).

La mayoría de las calculadoras gráficas y las utilidades gráficas pueden estimar la ubicación de máximos y mínimos. A continuación se muestran imágenes de pantalla de dos tecnologías diferentes, mostrando la estimación para el máximo y mínimo local.

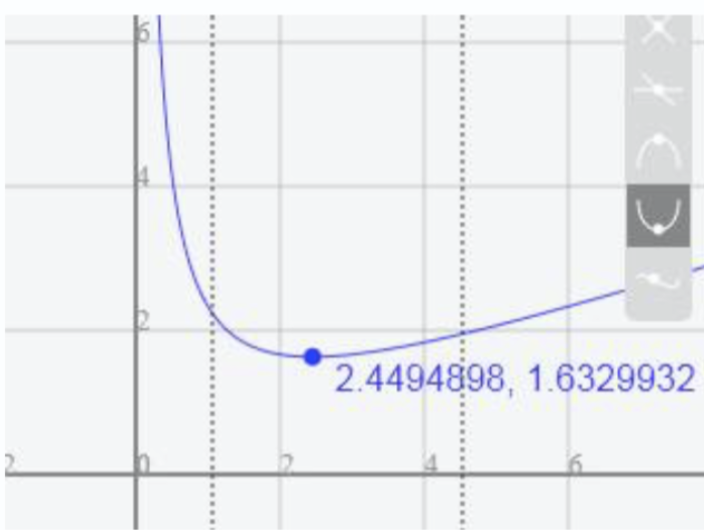
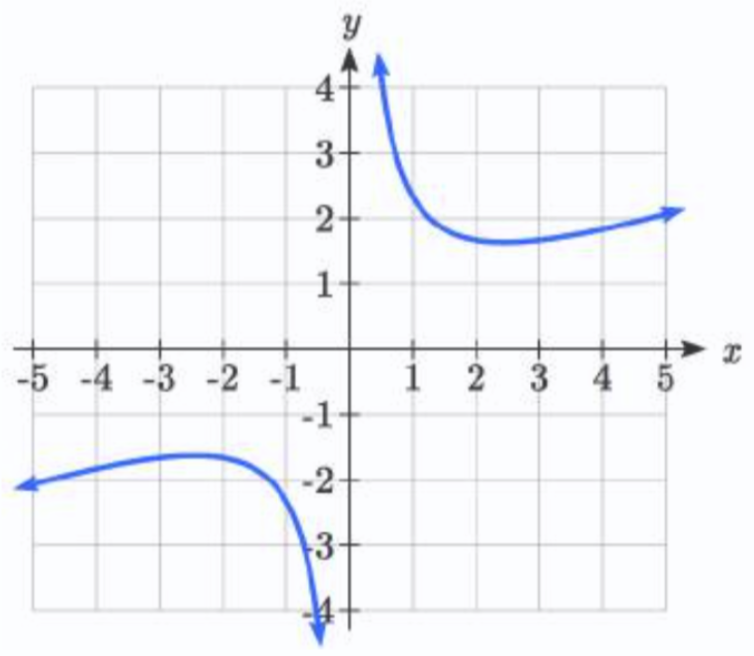
Con base en estas estimaciones, la función está aumentando en los intervalos\((-\infty , -2.449)\) y\((2.449, \infty )\). Observe que si bien esperamos que los extremos sean simétricos, las dos tecnologías diferentes coinciden solo hasta 4 decimales debido a los diferentes algoritmos de aproximación utilizados por cada una.

Ejercicio\(\PageIndex{4}\)

Utilice una gráfica de la función\(f(x)=x^{3} -6x^{2} -15x + 20\) para estimar los extremos locales de la función. Utilízalos para determinar los intervalos en los que la función está aumentando y disminuyendo.

Contestar

Con base en la gráfica, el máximo local parece ocurrir en (-1, 28), y el mínimo local ocurre en (5, -80). La función está aumentando\((-\infty, -1) \cup (5, \infty)\) y disminuyendo en (−1, 5).

Concavidad

Se muestran las ventas totales, en miles de dólares, para dos empresas de más de 4 semanas.

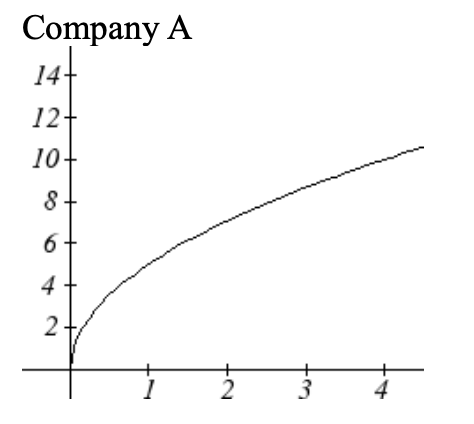
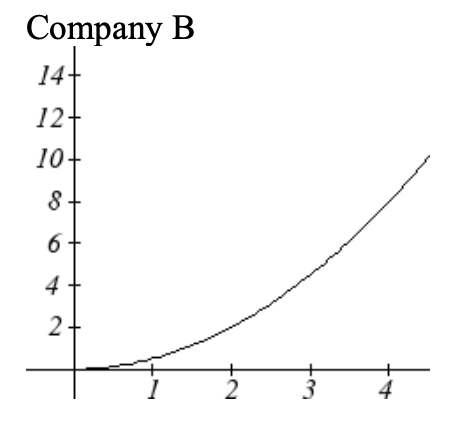
Como puede ver, las ventas para cada empresa van en aumento, pero van en aumento de formas muy diferentes. Para describir la diferencia de comportamiento, podemos investigar cómo varía la tasa promedio de cambio en diferentes intervalos. Usando tablas de valores,

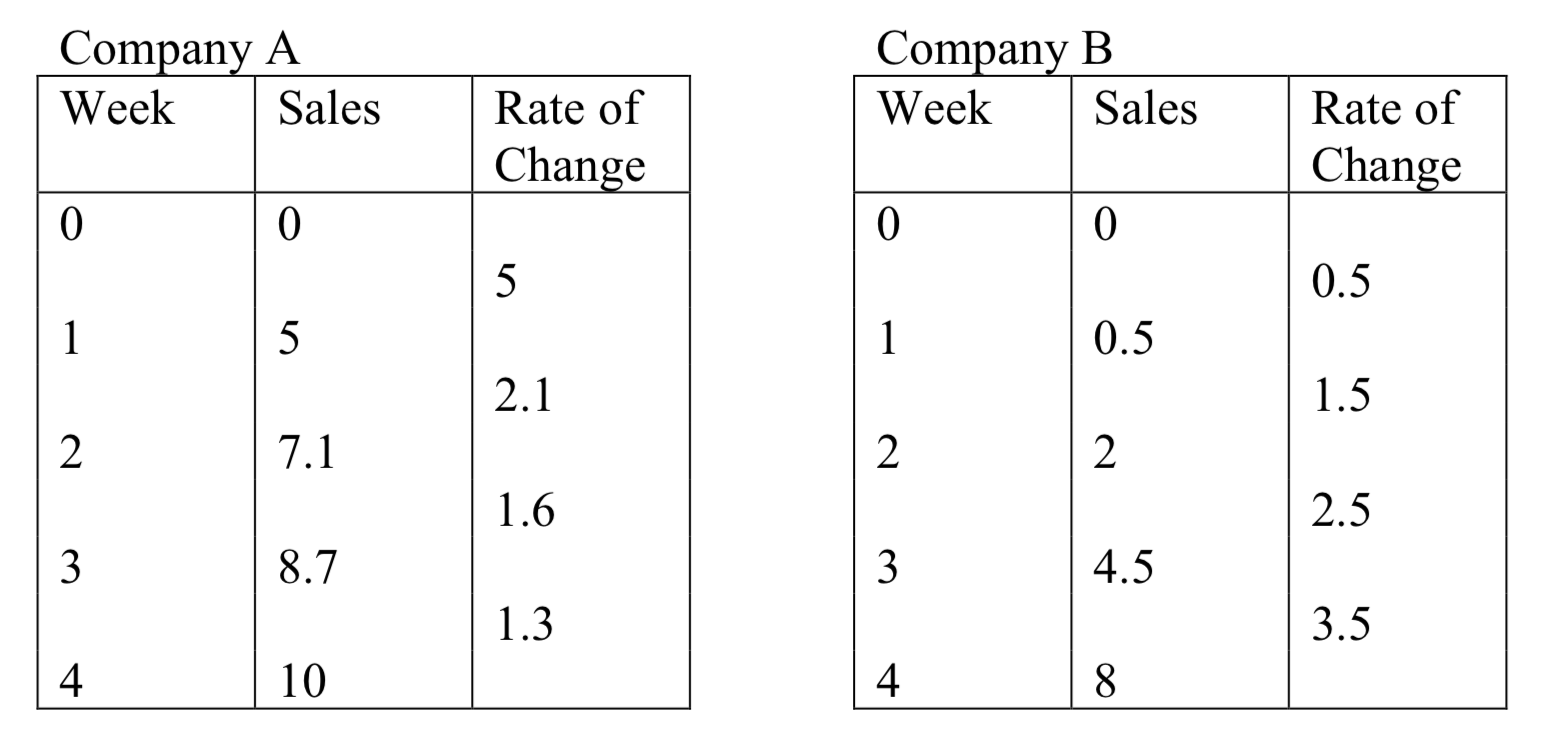
De las tablas, podemos ver que la tasa de cambio para la compañía A está disminuyendo, mientras que la tasa de cambio para la compañía B va en aumento.

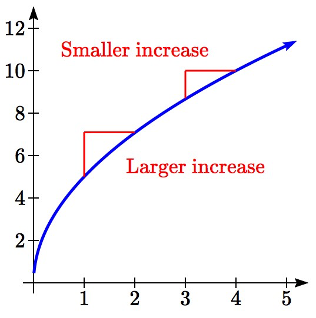
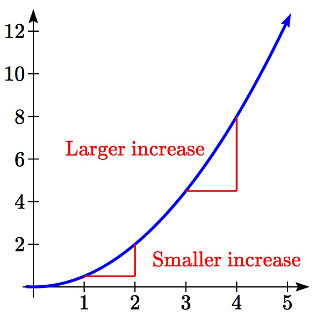
Cuando la tasa de cambio es cada vez más pequeña, al igual que con la Compañía A, decimos que la función es cóncava hacia abajo. Cuando la tasa de cambio es cada vez mayor, al igual que con la Compañía B, decimos que la función es cóncava hacia arriba.

Definición: concavidad

Una función es cóncava hacia arriba si la tasa de cambio está aumentando.

Una función es cóncava hacia abajo si la tasa de cambio está disminuyendo.

Un punto donde una función cambia de cóncava hacia abajo a cóncava o viceversa se denomina punto de inflexión.

Ejemplo\(\PageIndex{10}\)

Un objeto es arrojado desde lo alto de un edificio. La altura del objeto en pies sobre el suelo después de t segundos viene dada por la función\(h(t)=144 - 16t^{2}\) for\(0 \le t \le 3\). Describir la concavidad de la gráfica.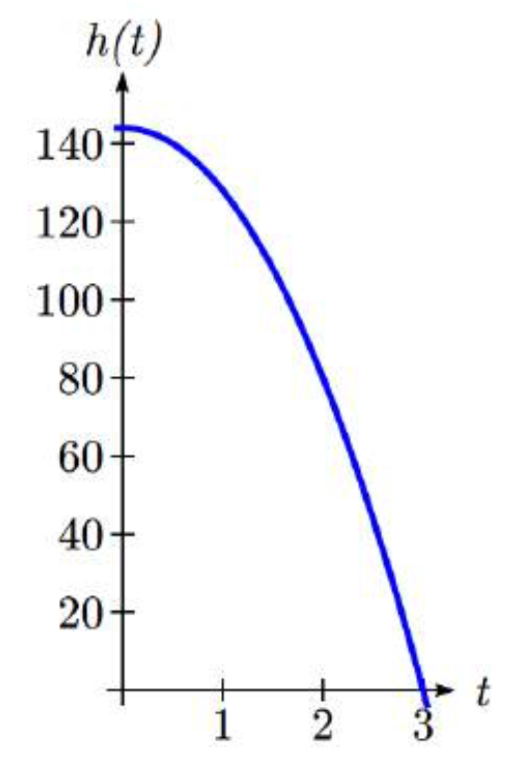

Al esbozar una gráfica de la función, podemos ver que la función está disminuyendo. Podemos calcular algunas tasas de cambio para explorar el comportamiento.

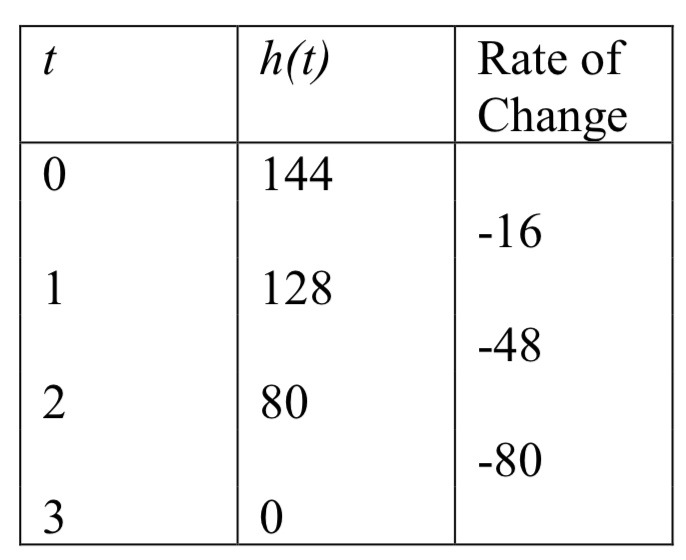
Observe que las tasas de cambio son cada vez más negativas, por lo que las tasas de cambio están disminuyendo. Esto significa que la función es cóncava hacia abajo.

Ejemplo\(\PageIndex{11}\)

El valor,\(V\), de un automóvil después de\(t\) años se da en la siguiente tabla. ¿El valor aumenta o disminuye? ¿La función es cóncava hacia arriba o cóncava hacia abajo?

Solución

puede calcular las tasas de cambio para determinar la concavidad.

Dado que estos valores son cada vez menos negativos, las tasas de cambio van en aumento, por lo que esta función es cóncava hacia arriba.

Ejercicio\(\PageIndex{5}\)

¿La función descrita en la tabla de abajo es cóncava hacia arriba o cóncava hacia abajo?

Contestar

Al calcular las tasas de cambio, vemos que las tasas de cambio se vuelven más negativas, por lo que las tasas de cambio están disminuyendo. Esta función es cóncava hacia abajo.

Gráficamente, las funciones cóncavas hacia abajo se doblan hacia abajo como un ceño fruncido y la función cóncava hacia arriba se dobla

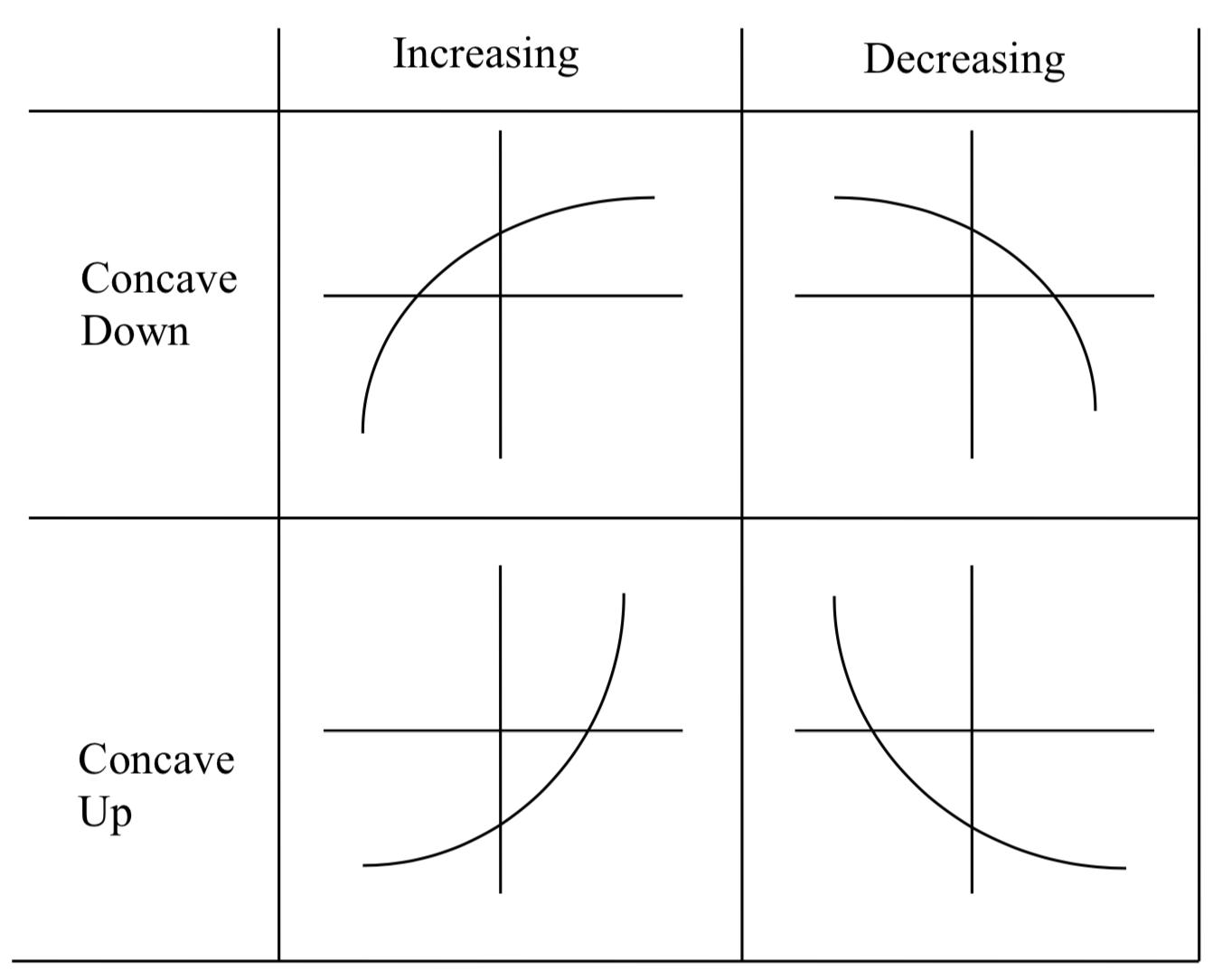
Ejemplo\(\PageIndex{12}\)

Estimar de la gráfica se muestran los intervalos en los que la función es cóncava hacia abajo y cóncava hacia arriba.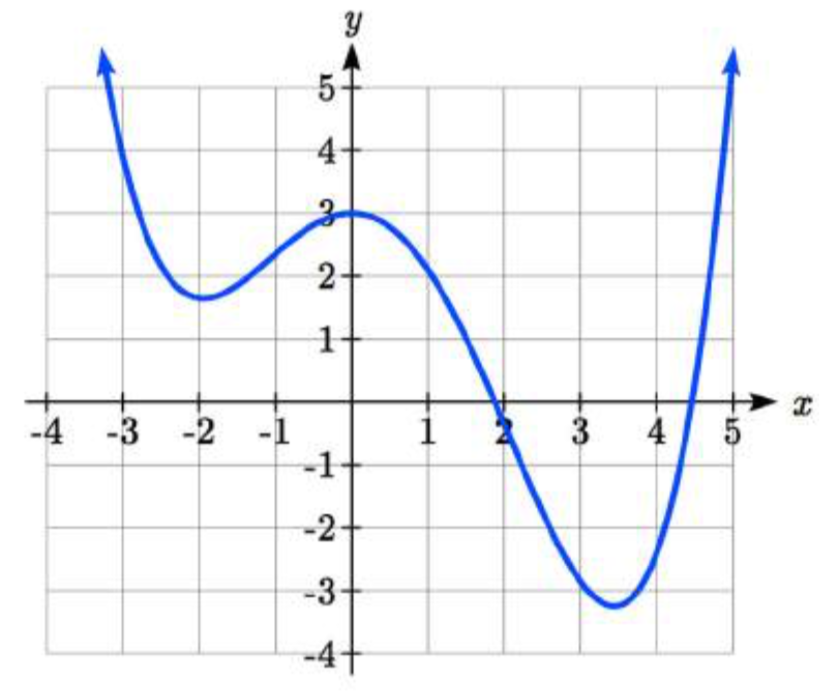

En el extremo izquierdo, la gráfica es decreciente pero cóncava hacia arriba, ya que se está doblando hacia arriba. Comienza a aumentar a las\(x = -2\), pero sigue doblándose hacia arriba hasta aproximadamente\(x = -1\).

A partir de\(x = -1\) la gráfica comienza a doblarse hacia abajo, y continúa haciéndolo hasta aproximadamente\(x = 2\). Luego, la gráfica comienza a curvarse hacia arriba para el resto de la gráfica mostrada.

A partir de esto, podemos estimar que la gráfica es cóncava hacia arriba en los intervalos\((-\infty, -1)\) y\((2, \infty)\), y es cóncava hacia abajo en el intervalo\((-1, 2)\). La gráfica tiene puntos de inflexión en\(x = -1\) y\(x = 2\).

Ejercicio\(\PageIndex{6}\)

Usando la gráfica de Pruébalo Ahora 4,\(f(x)=x^{3} -6x^{2} -15x+20\), estimar los intervalos en los que la función es cóncava hacia arriba y cóncava hacia abajo.

Contestar

Al mirar la gráfica, parece que la función es cóncava hacia abajo\((−\infty,2)\) y cóncava hacia arriba\((2, \infty)\).

Comportamientos de las funciones del kit de herramientas

Ahora volveremos a nuestras funciones de kit de herramientas y discutiremos su comportamiento gráfico.

Función	Aumentar/Disminuir	Concavidad
Función Constante \(f(x)=c\)	Ni aumentar ni disminuir	Ni cóncavos hacia arriba ni hacia abajo
Función Identidad \(f(x)=x\)	Incrementando	Ni cóncavos hacia arriba ni hacia abajo
Función cuadrática \(f(x)=x^{2}\)	Aumentando\((0,\infty )\) al disminuir en el\((-\infty ,0)\) mínimo en\(x = 0\)	Cóncavo\((-\infty ,\infty )\)
Función cúbica \(f(x)=x^{3}\)	Incrementando	Cóncavo hacia abajo en\((-\infty ,0)\) Cóncavo hacia arriba en el punto de\((0,\infty )\) inflexión en
Reciproca \(f(x)=\dfrac{1}{x}\)	Disminuyendo\((-\infty ,0) \cup (0,\infty )\)	Cóncavo abajo en\((-\infty ,0)\) Cóncavo\((0,\infty )\)
Función	Aumentar/Disminuir	Concavidad
Recíproco al cuadrado \(f(x)=\dfrac{1}{x^{2} }\)	Aumentando\((-\infty ,0)\) al disminuir el\((0,\infty )\)	Cóncavo hacia arriba\((-\infty ,0) \cup (0,\infty )\)
Raíz cúbica \(f(x)=\sqrt[{3}]{x}\)	Incrementando	Cóncavo hacia abajo en\((0,\infty )\) Cóncavo hacia arriba en el punto de\((-\infty ,0)\) inflexión en
Raíz cuadrada \(f(x)=\sqrt[{}]{x}\)	Aumentando en\((0,\infty )\)	Cóncavo hacia abajo\((0,\infty )\)
Valor Absoluto \(f(x)=\left|x\right|\)	Aumentando\((0, \infty )\) al disminuir el\((-\infty , 0)\)	Ni cóncavos hacia arriba ni hacia abajo

Temas Importantes de esta Sección

• Tasa de cambio
• Tasa promedio de cambio
• Cálculo de la tasa promedio de cambio usando la notación de funciones
• Aumentar/Disminuir
• Locales Maxima y Minima (Extrema)
• Puntos de inflexión
• Concavidad