1.3.3E: Tasas de Cambio y Comportamiento de las Gráficas

Última actualización
Guardar como PDF

Page ID: 116503

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Sección 1.3 EJERCICIO

La siguiente tabla da las ventas anuales (en millones de dólares) de un producto. ¿Cuál fue la tasa promedio de cambio de las ventas anuales...

a) Entre 2001 y 2002?
b) ¿Entre 2001 y 2004?

año	1998	1999	2000	2001	2002	2003	2004	2005	2006
ventas	201	219	233	243	249	251	249	243	233

El siguiente cuadro da la población de un pueblo, en miles. ¿Cuál fue la tasa promedio de cambio de la población...

a) Entre 2002 y 2004?
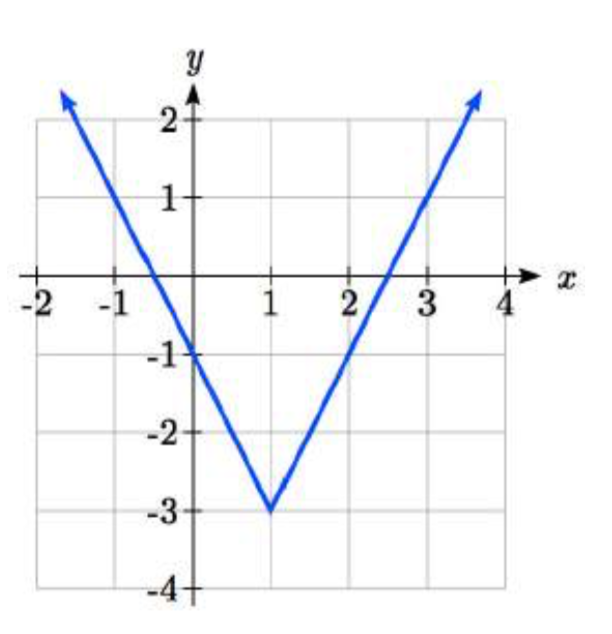
b) ¿Entre 2002 y 2006?

año	2000	2001	2002	2003	2004	2005	2006	2007	2008
población	87	84	83	80	77	76	75	78	81

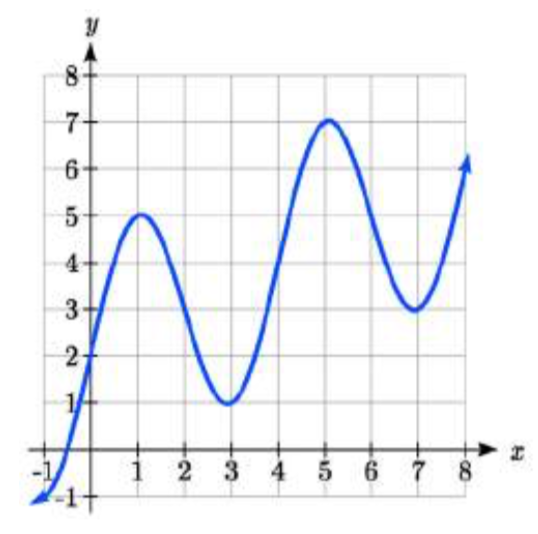
Con base en la gráfica mostrada, estimar la tasa promedio de cambio de$x = 1$ a$x = 4$. $2019-06-09 8.02.50.png$
Con base en la gráfica mostrada, estimar la tasa promedio de cambio de$x = 2$ a$x = 5$.

Encuentra la tasa promedio de cambio de cada función en el intervalo especificado.
$f(x)=x^{2}$en [1, 5]
$q(x)=x^{3}$el [-4, 2]
$g(x)=3x^{3} -1$el [-3, 3]
$h(x)=5 - 2x^{2}$el [-2, 4]
$k(t)=6t^{2} +\dfrac{4}{t^{3} }$en [-1, 3]
$p(t)=\dfrac{t^{2} - 4t + 1}{t^{2} + 3}$on [-3, 1]

Encuentra la tasa promedio de cambio de cada función en el intervalo especificado. Tus respuestas serán expresiones que involucren un parámetro ($b$o$h$).
$f(x)= 4x^{2} -7$en [1,$b$]
$g(x)= 2x^{2} -9$en [4,$b$]
$h(x)= 3x + 4$en [2, 2 +$h$]
$k(x)= 4x - 2$en [3, 3 +$h$]
$a(t)=\dfrac{1}{t + 4}$el [9, 9 +$h$]
$b(x)=\dfrac{1}{x + 3}$en [1, 1 +$h$]
$j(x)=3x^{3}$en [1, 1 +$h$]
$r(t)=4t^{3}$en [2, 2 +$h$]
$f(x)=2x^{2} + 1$en [$x$,$x + h$]
$g(x)=3x^{2} - 2$on [$x$,$x + h$]

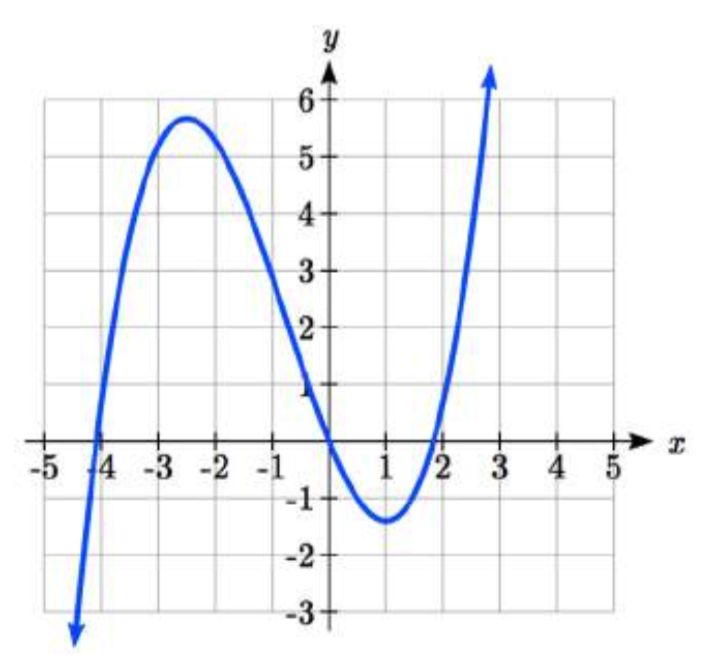
Para cada función graficada, estime los intervalos en los que la función está aumentando y disminuyendo.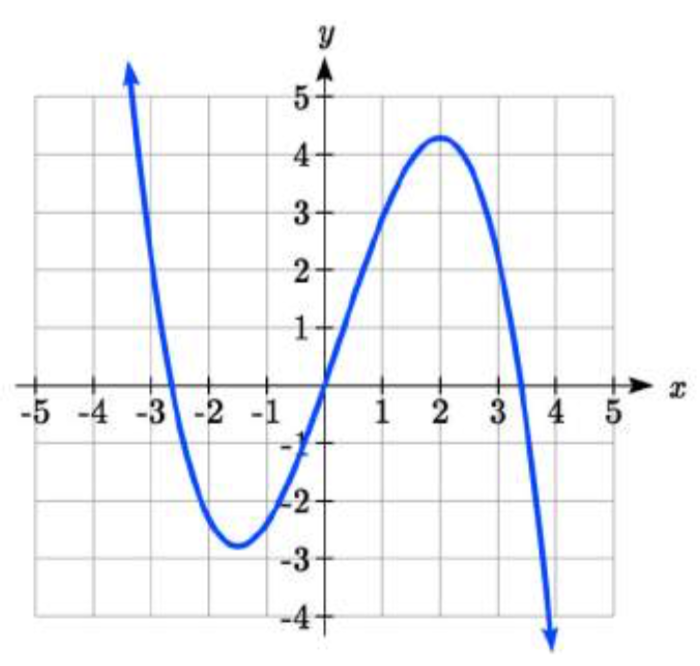
$2019-06-09 8.13.25.png$
$2019-06-09 8.13.46.png$
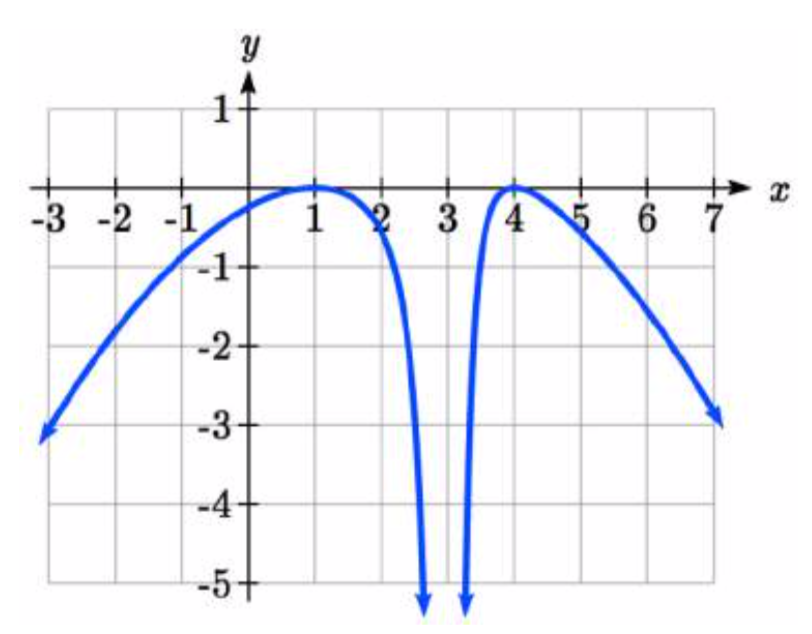
$2019-06-09 8.15.37.png$
$2019-06-09 8.16.18.png$

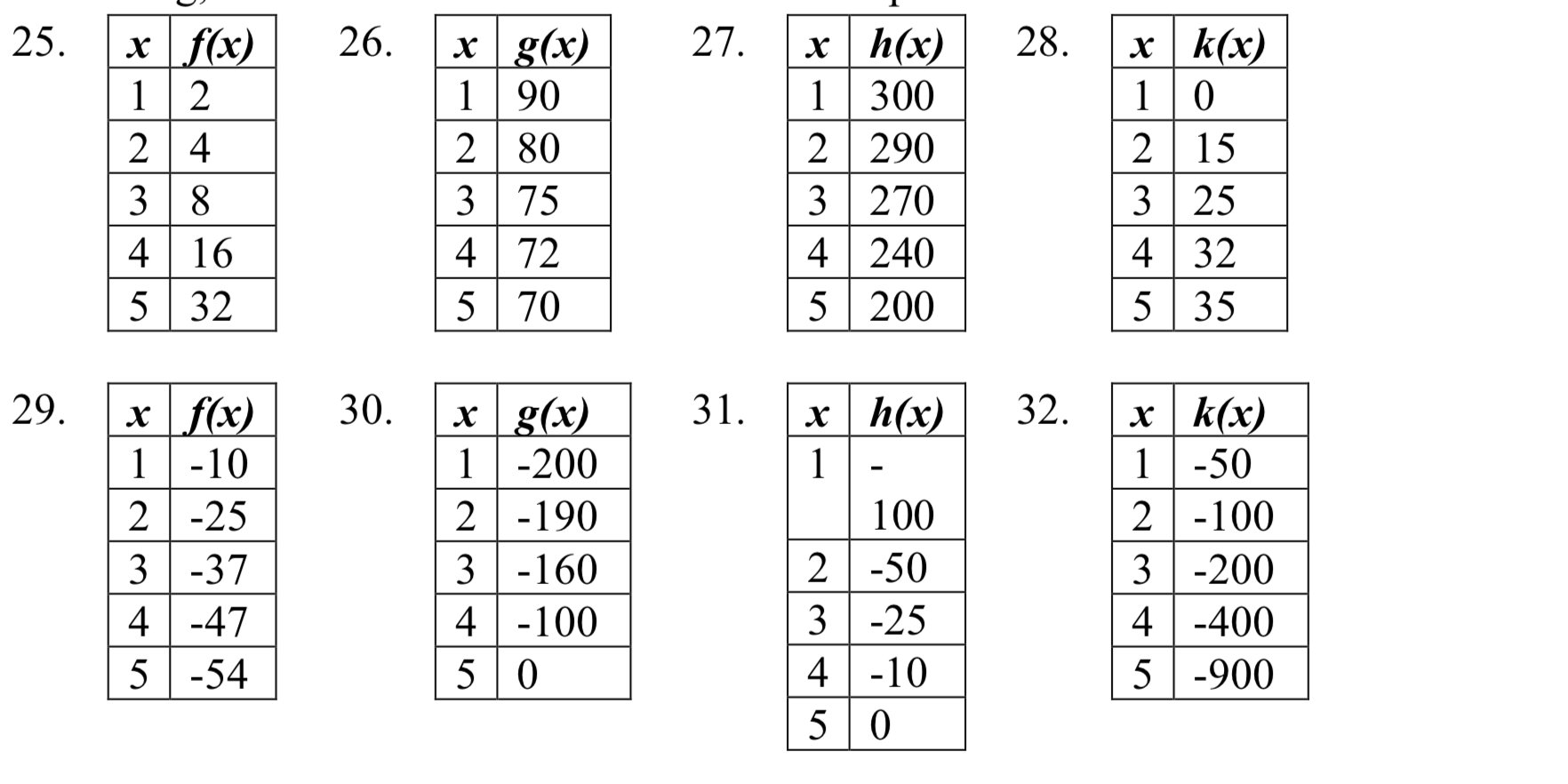
Para cada tabla a continuación, seleccione si la tabla representa una función que está aumentando o disminuyendo, y si la función es cóncava hacia arriba o cóncava hacia abajo.

$2019-06-09 8.18.21.png$

Para cada función graficada, estime los intervalos en los que la función es cóncava hacia arriba y hacia abajo, y la ubicación de cualquier punto de inflexión.

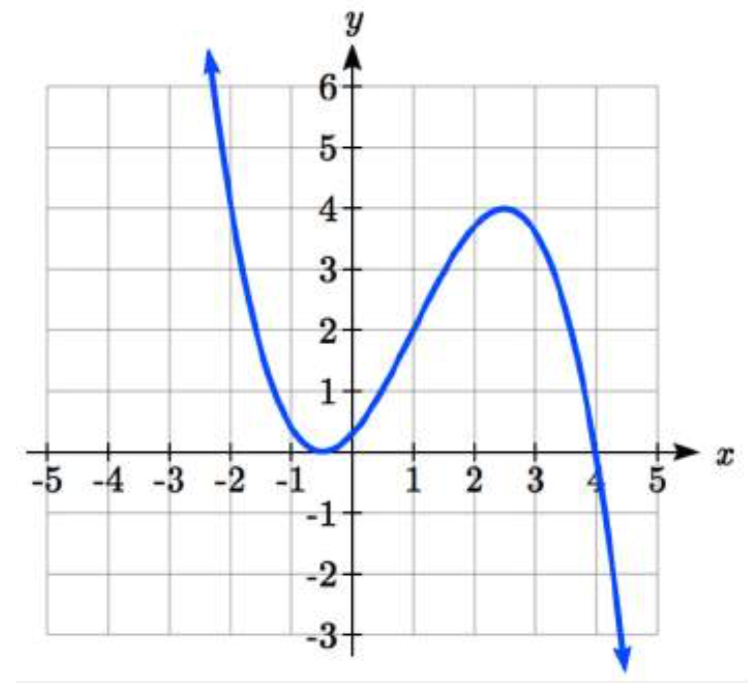
33. $2019-06-09 8.19.37.png$

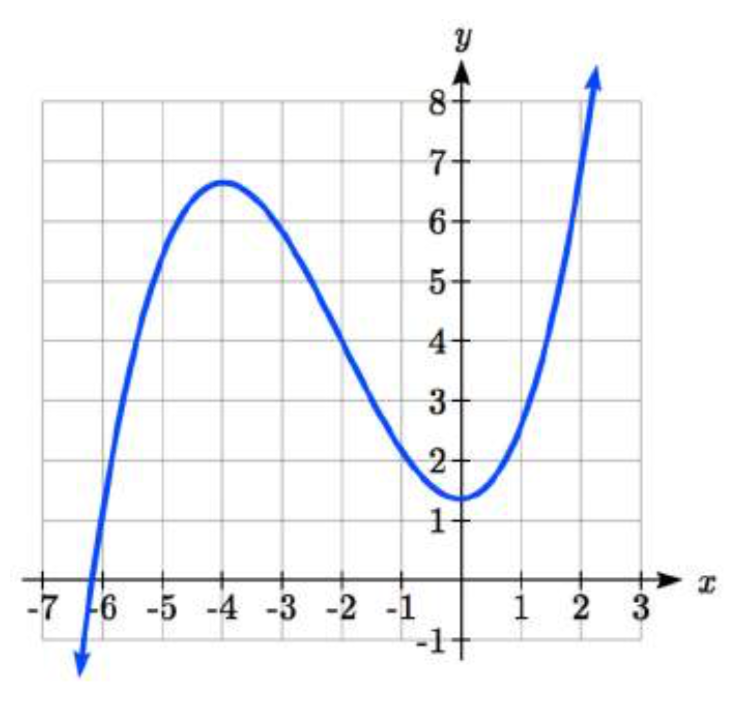
34. $2019-06-09 8.20.03.png$

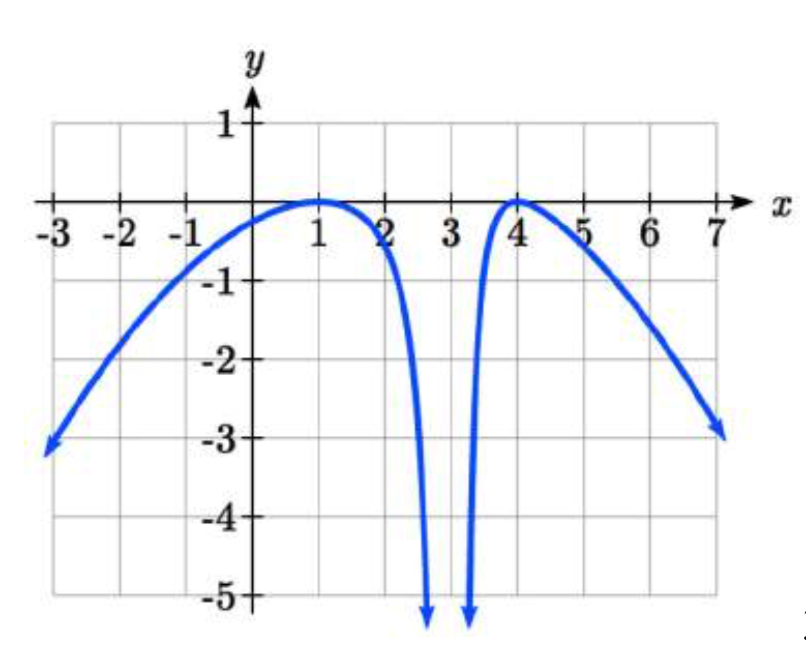
35. $2019-06-09 8.20.28.png$

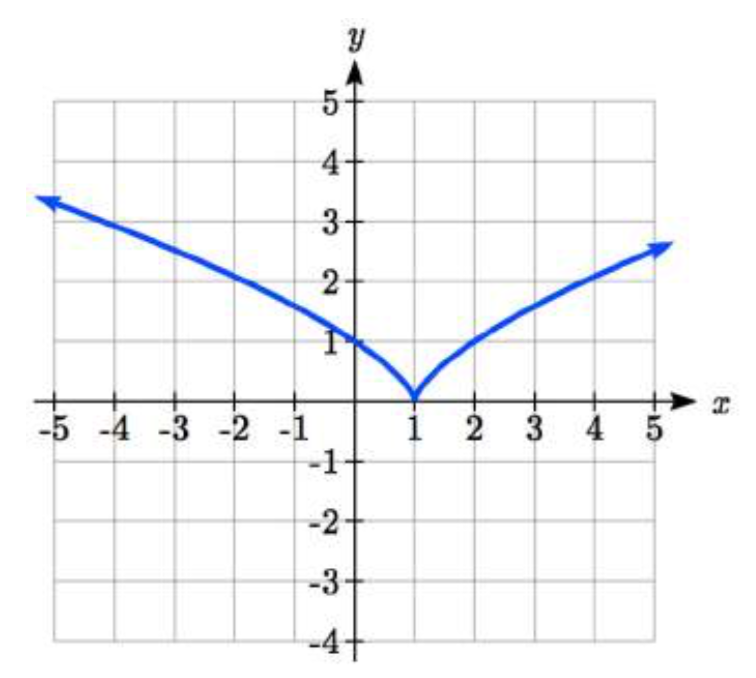
36. $2019-06-09 8.20.52.png$

Utilice una gráfica para estimar los extremos locales y los puntos de inflexión de cada función, y para estimar los intervalos en los que la función está aumentando, disminuyendo, cóncava hacia arriba y cóncava hacia abajo.

37. $f(x) = x^4 - 4x^3 + 5$

38. $h(x) = x^5 + 5x^4 + 10x^3 + 10x^2 - 1$

39. $g(t) = t \sqrt{t + 3}$

40. $k(t) = 3t^{\dfrac{2}{3}} - t$

41. $m(x) = x^4 + 2x^3 - 12x^2 - 10x + 4$

42. $n(x) = x^4 - 8x^3 + 18x^2 - 6x + 2$

Contestar

1. a) 6 millones de dólares anuales
b) 2 millones de dólares anuales

3. $\dfrac{4 - 5}{4 - 1} = -\dfrac{1}{3}$

5. 6

7. 27

9. $\dfrac{352}{27}$

11. $4b + 4$

13. 3

15. $-\dfrac{1}{13h + 169}$

17. $9 + 9h + 3h^2$

19. $4x + 2h$

21. Incrementando: (-1.5, 2). Disminución:$(-\infty, -1.4) \cup (2, \infty)$

23. Incrementando:$(-\infty, 1) \cup (3,4)$. Disminución:$(1, 3) \cup (4, \infty)$

25. Aumento, cóncavo hacia arriba

27. Disminución, cóncava abajo

29. Disminución, cóncava arriba

31. Creciente, cóncava hacia abajo

33. Cóncava hacia arriba$(-\infty, 1)$. Abajo cóncavo$(1, \infty)$. Punto de inflexión en (1, 2)

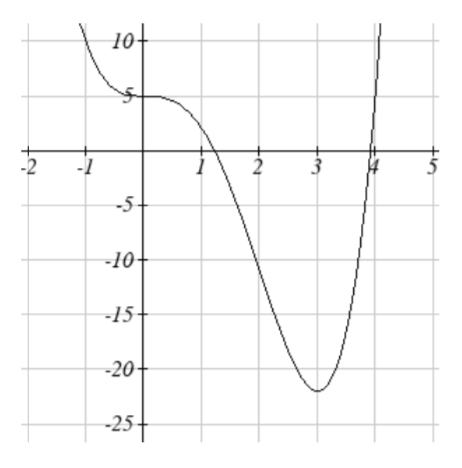$Screen Shot 2019-08-20 a las 11.41.13 AM.png$ 35. Cóncavo$-\infty, 3) \cup (3, \infty)$

37. Mínimo local en (3, -22).
Puntos de inflexión en (0, 5) y (2, -11).
Aumentando en$3, \infty)$. $(-\infty, 3)$
Concava decreciente hacia$(-\infty, 0) \cup (2, \infty)$ arriba Cóncavo hacia abajo (0, 2)

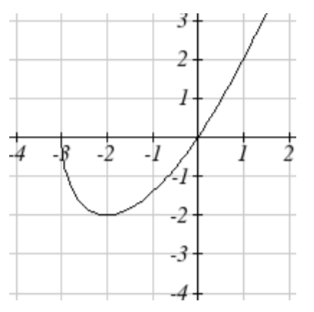
39. Mínimo local al$(-2, -2)$ $Screen Shot 2019-10-01 a las 8.53.49 AM.png$
disminuir (-3, -2)
Aumentando$(-2, \infty)$
cóncavo hacia arriba$(-3, \infty)$

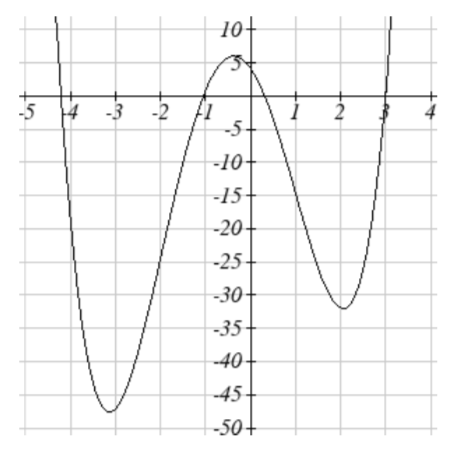
41. Mínimos locales en (-3.152, -47.626) y (2.041, -32.041) Máximo $Screen Shot 2019-10-01 a las 8.54.26 AM.png$
local en (-0.389, 5.979) Puntos de
inflexión en (-2, -24) y (1, -15)
Aumento$(-3.152, -0.389) \cup (2.041, \infty)$
decreciente$(-\infty, -3.152) \cup (-0.389, 2.041)$
Cóncavo hacia arriba$(-\infty, -2) \cup (1, \infty)$
Cóncavo hacia abajo (-2, 1

Search

Text Color

Text Size

Margin Size

Font Type