1.4: Composición de las funciones

Supongamos que queríamos calcular cuánto cuesta calentar una casa en un día determinado del año. El costo para calentar una casa dependerá de la temperatura media diaria, y la temperatura media diaria depende del día particular del año. Observe cómo acabamos de definir dos relaciones: La temperatura depende del día, y el costo depende de la temperatura. Usando variables descriptivas, podemos anotar estas dos funciones.

La primera función,\(C(T)\), da el costo\(C\) de calentar una casa cuando la temperatura media diaria es de\(T\) grados centígrados, y la segunda\(T(d)\),, da la temperatura media diaria el día\(d\) del año en alguna ciudad. Si quisiéramos determinar el costo de calentar la casa el\({}^{th}\) día 5 del año, podríamos hacer esto uniendo nuestras dos funciones, una idea llamada composición de funciones. Usando la función\(T(d)\), podríamos evaluar\(T(5)\) para determinar la temperatura promedio diaria a los 5\({}^{th}\) días del año. Entonces podríamos usar esa temperatura como entrada a la\(C(T)\) función para encontrar el costo para calentar la casa en el\({}^{th}\) día 5 del año:\(C(T(5))\).

Definición: Composición de las funciones

Cuando la salida de una función se usa como entrada de otra, llamamos a toda la operación una composición de funciones. Escribimos\(f(g(x))\), y leemos esto como “\(f\)\(g\)de\(x\)” o “\(f\)compuesto con\(g\) at\(x\)”.

Una notación alternativa para la composición usa el operador de composición:\(\circ\)

\((f \circ g)(x)\)se lee “\(f\)\(g\)de\(x\)” o “\(f\)compuesto con\(g\) at\(x\)”, al igual que\(f(g(x))\).

Ejemplo\(\PageIndex{1}\)

Supongamos que\(c(s)\) da la cantidad de calorías quemadas haciendo abdominales, y\(s(t)\) da la cantidad de abdominales que una persona puede hacer en t minutos. Interpretar\(c(s(3))\).

Solución

Cuando se nos pide que interpretemos, se nos pide que expliquemos el significado de la expresión en palabras. La expresión interior en la composición es\(s(3)\). Dado que la entrada a la función s es tiempo, el 3 representa 3 minutos, y\(s(3)\) es el número de abdominales que se pueden hacer en 3 minutos. Tomando esta salida y utilizarla como entrada a la\(c(s)\) función nos dará las calorías que se pueden quemar por el número de abdominales que se pueden hacer en 3 minutos.

Tenga en cuenta que no es importante que se utilice la misma variable para la salida de la función interior y la entrada a la función externa. Sin embargo, es esencial que las unidades en la salida de la función interior coincidan con las unidades en la entrada con la función externa, si se especifican las unidades.

Ejemplo\(\PageIndex{2}\)

Supongamos que\(f(x)\) da millas que se pueden conducir en\(x\) horas, y\(g(y)\) da los galones de gas utilizados para conducir\(y\) millas. ¿Cuál de estas expresiones tiene sentido:\(f(g(y))\) o\(g(f(x))\)?

Solución

La expresión\(g(y)\) toma millas como entrada y genera varios galones. La función\(f(x)\) está esperando un número de horas como entrada; tratar de darle un número de galones como entrada no tiene sentido. Recuerde que las unidades deben coincidir, y el número de galones no coincide con el número de horas, por lo que la expresión no\(f(g(y))\) tiene sentido.

La expresión\(f(x)\) toma horas como entrada y genera un número de millas recorridas. La función\(g(y)\) espera un número de millas como entrada, por lo que dar la salida de la\(f(x)\) función (millas conducidas) como un valor de entrada para\(g(y)\), donde los galones de gas dependen de las millas conducidas, tiene sentido. La expresión tiene\(g(f(x))\) sentido, y dará el número de galones de gas utilizados,\(g\), conduciendo un cierto número de millas,\(f(x)\), en\(x\) horas.

Ejercicio\(\PageIndex{1}\)

En una tienda departamental se ve un letrero que dice 50% de descuento en mercancía de despacho, por lo que el costo final\(C\) depende del precio de despacho\(p\),, según la función\(C(p)\). Precio de liquidación\(p\),, depende del descuento original,\(d\), dado al artículo de despacho,\(p(d)\). Interpretar\(C(p(d))\).

Contestar

El costo final,\(C\), depende del precio de despacho,\(p\), que se basa en el descuento original,\(d\). (O el descuento original\(d\), determina el precio de despacho y el costo final es la mitad del precio de despacho).

Composición de Funciones mediante Tablas y Gráficas

Al trabajar con funciones dadas como tablas y gráficas, podemos buscar valores para las funciones usando una tabla o gráfica proporcionada, como se explica en la sección 1.1. Comenzamos la evaluación a partir de la entrada proporcionada, y primero evaluamos la función interna. Entonces podemos usar la salida de la función inside como la entrada a la función externa. Para recordar esto, siempre trabaja de adentro hacia afuera.

Ejemplo\(\PageIndex{3}\)

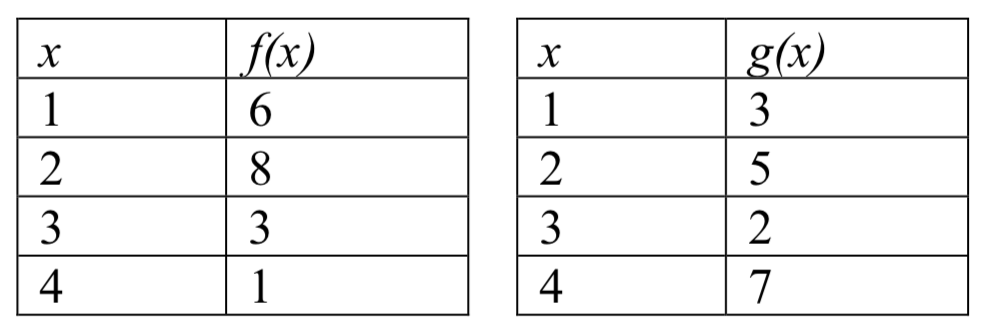
Usando las tablas a continuación, evaluar\(f(g(3))\) y\(g(f(4))\)

Solución

Para evaluar\(f(g(3))\), partimos desde el interior con el valor 3. Luego evaluamos la expresión interior\(g(3)\) usando la tabla que define la función\(g: g(3) = 2\).

Entonces podemos usar ese resultado como la entrada a la\(f\) función, por lo que\(g(3)\) se sustituye por el valor equivalente 2 y podemos evaluar\(f(2)\). Después usando la tabla que define la función\(f\), nos encontramos con eso\(f(2) = 8\).

\[f(g(3))=f(2)=8. \nonumber\]

Para evaluar\(g(f(4))\), primero evaluamos la expresión interna\(f(4)\) usando la primera tabla:\(f(4) = 1\). Luego usando la tabla para\(g\) podemos evaluar:

\[g(f(4))=g(1)=3. \nonumber\]

Ejercicio\(\PageIndex{2}\)

Usando las tablas del ejemplo anterior, evaluar\(f(g(1))\) y\(g(f(3))\).

Contestar

\(f(g(1)) = f(3) = 3\)y\(g(f(3)) = g(3) = 2\)

Ejemplo\(\PageIndex{4}\)

Usando las gráficas a continuación, evalúe\(f(g(1))\).

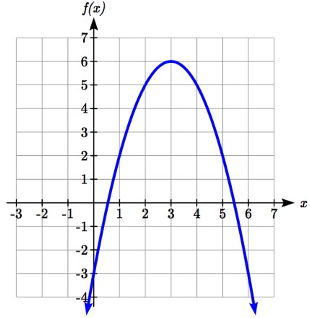
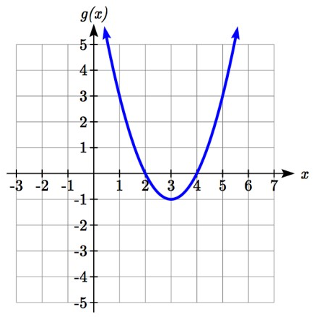
Para evaluar\(f(g(1))\), nuevamente comenzamos con la evaluación interna. Evaluamos\(g(1)\) usando la gráfica de la función g (x), encontrando la entrada de 1 en el eje horizontal y encontrando el valor de salida de la gráfica en esa entrada. Aquí,\(g(1) = 3\).

Usando este valor como entrada a la función f,\(f(g(1))=f(3)\). Luego podemos evaluar esto mirando a la gráfica de la\(f(x)\) función, encontrando la entrada de 3 en el eje horizontal y leyendo el valor de salida de la gráfica en esta entrada.

\(f(3) = 6\), entonces\(f(g(1))=6\).

Ejercicio\(\PageIndex{3}\)

Utilizando las gráficas del ejemplo anterior, evalúe\(g(f(2))\).

Contestar

\(g(f(2)) = g(5) = 3\)

Composición usando Fórmulas

Al evaluar una composición de funciones donde ya sea hemos creado o se nos han dado fórmulas, el concepto de trabajar de adentro hacia afuera sigue siendo el mismo. Primero, evaluamos la función inside usando el valor de entrada proporcionado, luego usamos la salida resultante como la entrada a la función externa.

Ejemplo\(\PageIndex{5}\)

Dado\(f(t)=t^{2} -t\) y\(h(x)=3x + 2\), evaluar\(f(h(1))\).

Solución

Dado que la evaluación interna es\(h(1)\) comenzamos evaluando la\(h(x)\) función en 1:

\[h(1) = 3(1) + 2 = 5\nonumber \]

Luego\(f(h(1))=f(5)\), así evaluamos la función f (t) a una entrada de 5:

\[f(h(1)) = f(5) = 5^{2} - 5 = 20\nonumber \]

Ejercicio\(\PageIndex{4}\)

Usando las funciones del ejemplo anterior, evalúe\(h(f(-2))\).

Contestar

\(h(f(-2)) = h(6) = 20\)(¿Te acordaste de insertar tus valores de entrada usando paréntesis? )

Si bien podemos componer las funciones como se indicó anteriormente para cada valor de entrada individual, a veces sería muy útil encontrar una sola fórmula que calculara el resultado de una composición f (g (x)). Para ello, ampliaremos nuestra idea de evaluación de funciones. Recordemos que cuando evaluamos una función como\(f(t)=t^{2} -t\), ponemos cualquier valor que esté dentro de los paréntesis después del nombre de la función en la fórmula dondequiera que veamos la variable de entrada.

Ejemplo\(\PageIndex{6}\)

Dado\(f(t) = t^{2} - t\), evaluar\(f(3)\) y\(f(-2)\).

Solución

\[ \begin{align*} f(3) &= 3^2 - 3 \\[4pt] f(-2) &= (-2)^2 - (-2)\end{align*} \]

Podríamos simplificar los resultados anteriores si quisiéramos

\[ \begin{align*} f(3) &= 3^2 - 3 = 9 - 3 = 6 \\[4pt] f(-2) &= (-2)^2 - (-2) = 4 + 2 = 6 \end{align*}\]

No estamos limitados, sin embargo, a usar un valor numérico como entrada a la función. Podemos poner cualquier cosa en la función: un valor, una variable diferente, o incluso una expresión algebraica, siempre que usemos la expresión de entrada en todas partes donde veamos la variable de entrada.

Ejemplo\(\PageIndex{7}\)

Usando la función del ejemplo anterior, evalúe f (a).

Solución

Esto significa que el valor de entrada para\(t\) es alguna cantidad desconocida\(a\). Como antes, evaluamos reemplazando la variable\(t\) de entrada por la cantidad de entrada, en este caso\(a\).

\[f(a)=a^{2} - a\nonumber \]

La misma idea se puede aplicar entonces a expresiones más complicadas que una sola letra.

Ejemplo\(\PageIndex{8}\)

Usando la misma\(f(t)\) función desde arriba, evalúe\(f(x + 2)\).

Solución

En todas partes en la fórmula para f donde hubiera una t, la reemplazaríamos con la entrada\((x+2)\). Dado que en la fórmula original la entrada t estaba al cuadrado en el primer término, toda la entrada\(x+2\) necesita ser cuadrada cuando sustituimos, por lo que necesitamos usar paréntesis de agrupación. Para evitar problemas, es recomendable usar siempre paréntesis alrededor de las entradas.

\[f(x+2)=(x+2)^{2} -(x+2)\nonumber \]

Podríamos simplificar aún más esta expresión\(f(x+2)=x^{2} +3x+2\) si quisiéramos:

\[f(x+2)=(x+2)(x+2)-(x+2)\nonumber \]

Utilizar la técnica “FOIL” (primero, exterior, interior, último)

\[f(x+2)=x^{2} +2x+2x+4-(x+2)\nonumber \]

distribuir el signo negativo

\[f(x+2)=x^{2} +2x+2x+4-x-2\nonumber \]

combinar términos similares

\[f(x+2)=x^{2} +3x+2\nonumber \]

Ejemplo\(\PageIndex{9}\)

Usando la misma función, evaluar\(f(t^{3} )\).

Solución

Tenga en cuenta que en este ejemplo, se usa la misma variable en la expresión de entrada y como la variable de entrada de la función. Esto no importa — seguimos reemplazando la entrada original t en la fórmula con la nueva expresión de entrada,\(t^{3}\).

\[f(t^{3} )=(t^{3} )^{2} -(t^{3} )=t^{6} - t^{3}\nonumber \]

Ejercicio\(\PageIndex{5}\)

Dado\(g(x) = 3x - \sqrt{x}\), evaluar\(g(t - 2)\).

Contestar

\[g(t - 2) = 3(t - 2) - \sqrt{(t - 2)}\nonumber \]

Esto ahora nos permite encontrar una expresión para una composición de funciones. Si queremos encontrar una fórmula para\(f(g(x))\), podemos comenzar por escribir la fórmula para\(g(x)\). Luego podemos evaluar la función\(f(x)\) en esa expresión, como en los ejemplos anteriores.

Ejemplo\(\PageIndex{10}\)

Dejar\(f(x)=x^{2}\) y\(g(x)=\dfrac{1}{x} -2x\), encontrar\(f(g(x))\) y\(g(f(x))\).

Solución

Para encontrar\(f(g(x))\), comenzamos evaluando el interior, escribiendo la fórmula para\(g(x)\).

\[g(x)=\dfrac{1}{x} -2x\nonumber \]

Luego usamos la expresión\((\dfrac{1}{x} -2x)\) como entrada para la función\(f\).

\[f(g(x)) = f(\dfrac{1}{x} - 2x)\nonumber \]

Luego evaluamos la función\(f(x)\) usando la fórmula para\(g(x)\) como entrada.

Dado que\(f(x)=x^{2}\),

\[f(\dfrac{1}{x} -2x) = (\dfrac{1}{x} - 2x)^{2}\nonumber \]

Esto nos da la fórmula para la composición:

\[f(g(x)) = (\dfrac{1}{x} - 2x)^{2}\nonumber \]

Asimismo, para encontrar g (f (x)), evaluamos el interior, escribiendo la fórmula para f (x)

\[g(f(x))=g(x^{2})\nonumber \]

Ahora evaluamos la función g (x) usando\(x^{2}\) como entrada.

\[g(f(x))=\dfrac{1}{x^{2} } -2x^{2}\nonumber \]

Ejercicio\(\PageIndex{6}\)

Dejar\(f(x) = x^{3} +3x\) y\(g(x)=\sqrt{x}\), encontrar\(f(g(x))\) y\(g(f(x))\).

Contestar

\[f(g(x) = f(\sqrt{x}) = (\sqrt{x})^3 + 3(\sqrt{x})\nonumber \]

\[g(f(x) = g(x^3 + 3x) = \sqrt{(x^3 + 3x)}\nonumber \]

Ejemplo\(\PageIndex{11}\)

Un administrador municipal determina que los ingresos fiscales,\(R\), en millones de dólares recaudados a una población de\(p\) mil personas, viene dado por la fórmula\(R(p) = 0.03p + \sqrt{p}\), y que se prevé que la población de la ciudad, en miles, siga la fórmula\(p(t) = 60 + 2t + 0.3t^{2}\), donde t se mide en años posteriores a 2010. Encuentre una fórmula para los ingresos fiscales en función del año.

Solución

Como queremos que los ingresos fiscales sean una función del año, queremos que el año sea nuestro insumo inicial, y que los ingresos sean nuestro producto final. Para encontrar ingresos, primero tendremos que predecir la población de la ciudad, y luego usar ese resultado como insumo para la función fiscal. Entonces tenemos que encontrar\(R(p(t))\). Evaluando esto,

\[R(p(t)) = R(60 + 2t + 0.3t^{2} ) = 0.03(60+2t+0.3t^{2}) + \sqrt{60 + 2t + 0.3t^{2} }\nonumber \]

Esta composición nos da una fórmula única que puede ser utilizada para predecir los ingresos fiscales durante un año determinado, sin necesidad de encontrar el valor de la población intermediaria.

Por ejemplo, para predecir los ingresos fiscales en 2017, cuando t = 7 (porque t se mide en años posteriores a 2010),

\[R(p(7))=0.03(60 + 2(7) + 0.3(7)^{2})+ \sqrt{60 + 2(7) + 0.3(7)^{2} } \approx 12.079\text{ million dollars}\nonumber \]

Dominio de las Composiciones

Cuando pensamos en el dominio de una composición\(h(x)=f(g(x))\), debemos considerar tanto el dominio de la función interna como el dominio de la composición misma. Si bien es tentador solo mirar la función compuesta resultante, si la función interna fuera indefinida a un valor de\(x\), la composición no sería posible.

Ejemplo\(\PageIndex{12}\)

Dejar\(f(x)=\dfrac{1}{x^{2} -1}\) y\(g(x)=\sqrt{x-2}\). Encuentra el dominio de\(f(g(x))\).

Ya que queremos evitar la raíz cuadrada de los números negativos, el dominio de\(g(x)\) es el conjunto de valores donde\(x - 2 \ge 0\). El dominio es\(x \ge 2\).

La composición es\[f(g(x))=\dfrac{1}{(\sqrt{x-2})^{2} - 1} = \dfrac{1}{(x - 2)-1} = \dfrac{1}{x - 3}\nonumber \].

La composición es indefinida cuando\(x = 3\), por lo que ese valor también debe ser excluido del dominio. Observe que la composición no implica una raíz cuadrada, pero aún tenemos que considerar la limitación de dominio desde la función interna.

Combinando las dos restricciones, el dominio es todos los valores de x mayores o iguales a 2, excepto\(x = 3\).

En las desigualdades, el dominio es:\(2 \le x<3\) o\(x > 3\)

En notación de intervalos, el dominio es:\([2, 3) \cup (3, \infty)\).

Ejercicio\(\PageIndex{7}\)

Dejar\(f(x) = \dfrac{1}{x-2}\) y\(g(x)=\dfrac{1}{x}\). Encuentra el dominio de\(f(g(x))\).

Contestar

\(g(x) = \dfrac{1}{x}\)está indefinido en\(x = 0\).

La composición, no\[f(g(x)) = f(\dfrac{1}{x}) = \dfrac{1}{\dfrac{1}{x} - 2} = \dfrac{1}{\dfrac{1}{x} - \dfrac{2x}{x}} = \dfrac{1}{\dfrac{1 - 2x}{x}} = \dfrac{x}{1 - 2x}\nonumber \] está definida cuando\(1 - 2x = 0\), cuando\(x = \dfrac{1}{2}\).

Restringiendo estos dos valores, el dominio es\((-\infty, 0) \cup (0, \dfrac{1}{2}) \cup (\dfrac{1}{2}, \infty)\)

Funciones de descomposición

En algunos casos, es deseable descomponer una función —escribirla como una composición de dos funciones más simples.

Ejemplo\(\PageIndex{13}\)

Escribir\(f(x)=3+\sqrt{5 - x^{2} }\) como la composición de dos funciones.

Solución

Estamos buscando dos funciones,\(g\) y\(h\), entonces\(f(x) = g(h(x))\). Para ello, buscamos una función dentro de una función en la fórmula para\(f(x)\). Como una posibilidad, podríamos notar que\(5 - x^{2}\) es el interior de la raíz cuadrada. Entonces podríamos descomponer la función como:

\[h(x)=5-x^{2}\nonumber \]

\[g(x)=3+\sqrt{x}\nonumber \]

Podemos verificar nuestra respuesta recomponiendo las funciones:

\[g(h(x)) = g(5 - x^{2})=3 + \sqrt{5-x^2 }\nonumber \]

Tenga en cuenta que esta no es la única solución al problema. Otra descomposición no trivial sería\(h(x) = x^{2}\) y\(g(x) = 3 + \sqrt{5-x}\)

Temas Importantes de esta Sección

• Definición de composición de funciones
• Composiciones que utilizan:
• Palabras
• Mesas
• Gráficas
• Ecuaciones
• Dominio de las Composiciones
• Descomposición de funciones