1.5.5E: Transformación de Funciones
- Page ID
- 116469
Sección 1.5 Ejercicios
Describir cómo cada función es una transformación de la función original\(f(x)\)
1. \(f(x - 49)\)
2. \(f(x + 43)\)
3. \(f(x+3)\)
4. \(f(x-4)\)
5. \(f(x)+5\)
6. \(f(x)+8\)
7. \(f(x)-2\)
8. \(f(x)-7\)
9. \(f(x-2)+3\)
10. \(f(x+4)-1\)
11. Escribe una fórmula para\(f(x)=\sqrt{x}\) desplazada hacia arriba 1 unidad e izquierda 2 unidades.
12. Escribe una fórmula para\(f(x)=|x|\) desplazada hacia abajo 3 unidades y derecha 1 unidad.
13. Escribe una fórmula para\(f(x)=\dfrac{1}{x}\) desplazada hacia abajo 4 unidades y derecha 3 unidades.
14. Escribe una fórmula para\(\; f(x)=\dfrac{1}{x^{2} }\) desplazada hacia arriba 2 unidades e izquierda 4 unidades.
15. Las tablas de valores para\(f(x)\),\(g(x)\), y\(h(x)\) se dan a continuación. Escribir\(g(x)\) y\(h(x)\) como transformaciones de\(f(x)\).
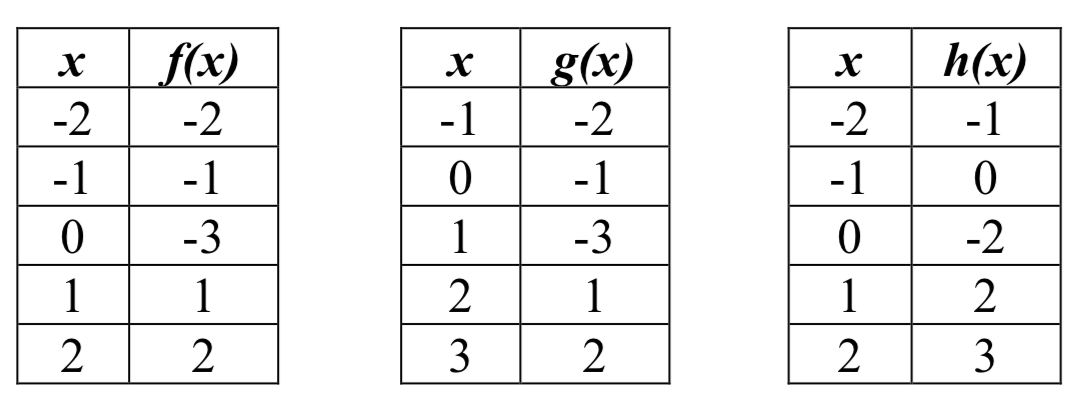
16. Las tablas de valores para\(f(x)\),\(g(x)\), y\(h(x)\) se dan a continuación. Escribir\(g(x)\) y\(h(x)\) como transformaciones de\(f(x)\).

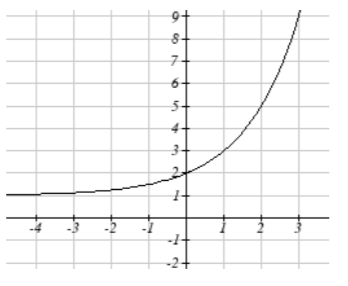
Se muestra la\(f(x)=2^{x}\) gráfica de. Esbozar una gráfica de cada transformación de\(f(x)\).
17. \(g(x)=2^{x} +1\)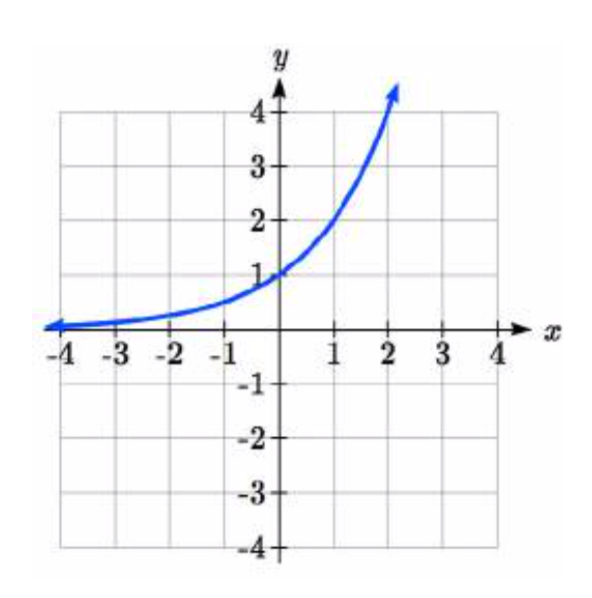
18. \(h(x)=2^{x} -3\)
19. \(w(x)=2^{x-1}\)
20. \(q(x)=2^{x+3}\)
Esboce un gráfico de cada función como una transformación de una función de kit de herramientas.
21. \(f(t)=(t+1)^{2} -3\)
22. \(h(x)=|x-1|+4\)
23. \(k(x=(x-2)^{3} -1\)
24. \(m(t)=3+\sqrt{t+2}\)
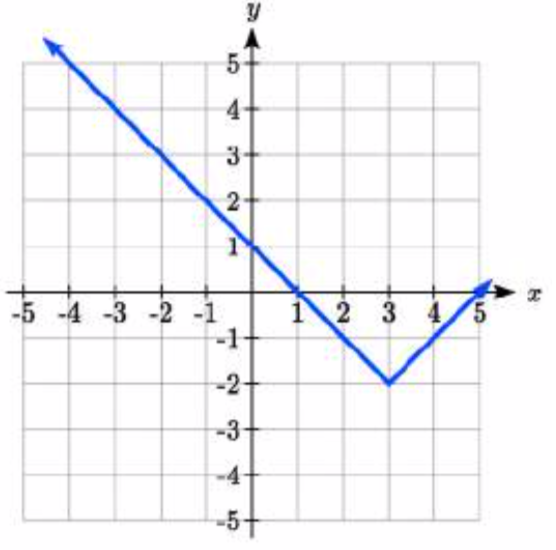
Escribe una ecuación para cada función graficada a continuación.
25. 
26. 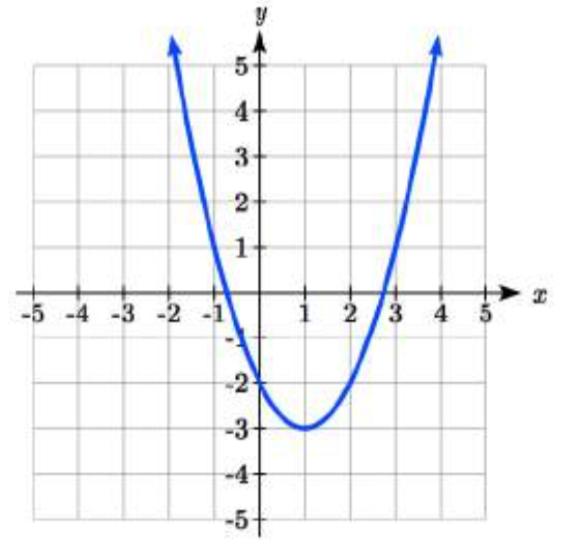
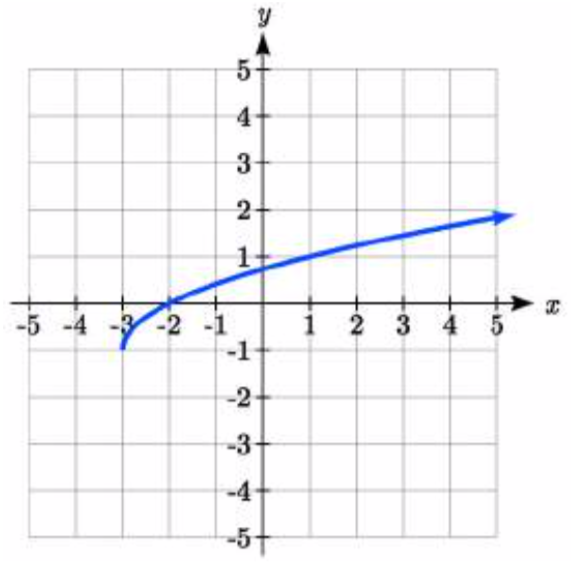
27. 
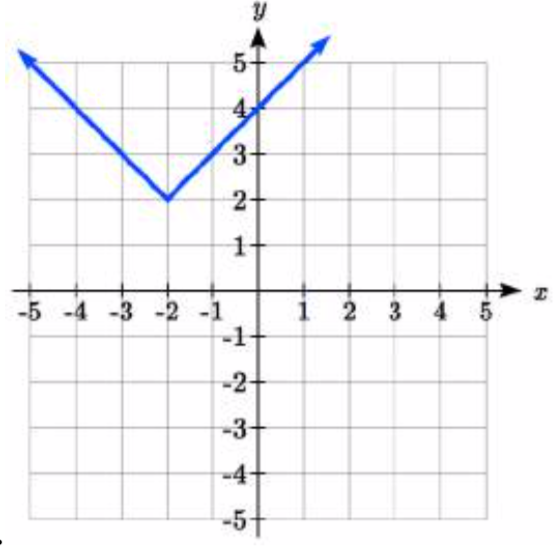
28. 
Encuentra una fórmula para cada una de las transformaciones de la raíz cuadrada cuyas gráficas se dan a continuación.
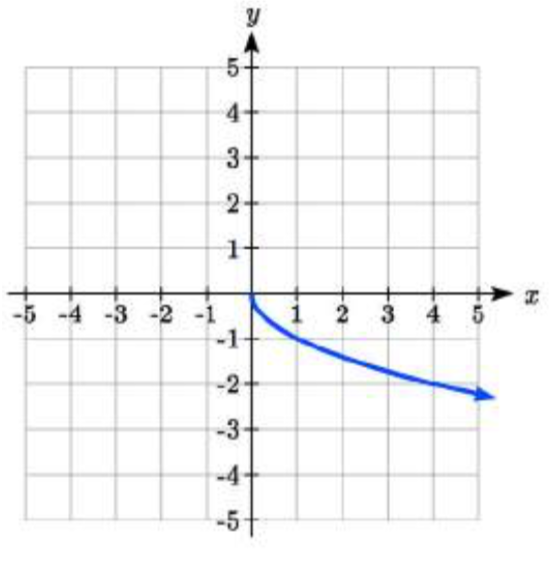
29. 
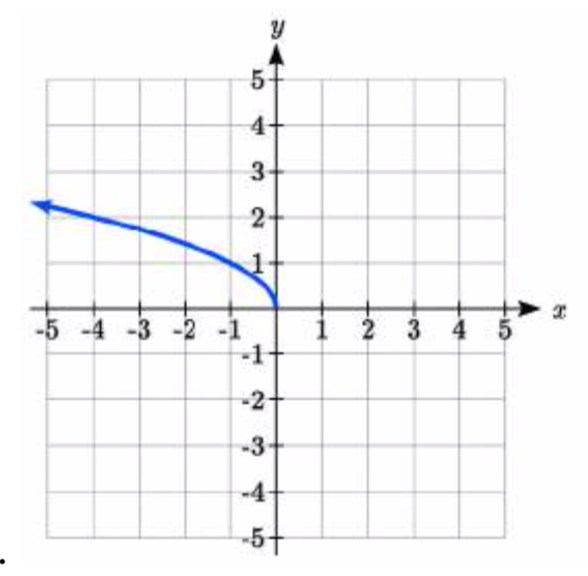
30. 
Se muestra la\(f(x)=2^{x}\) gráfica de. Esbozar un gráfico de cada transformación de\(f(x)\)
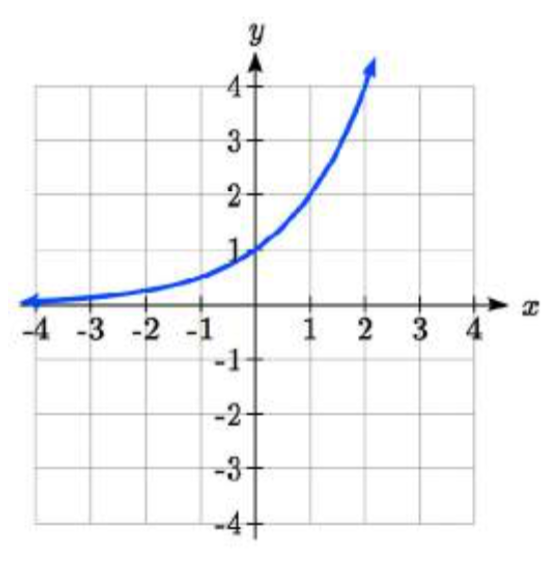
31. \(g(x)=-2^{x} +1\)
32. \(h(x)=2^{-x}\)
33. Comenzando con la gráfica de\(f(x)= 6^{x}\) escribir la ecuación de la gráfica que resulta de
a. reflexionando\(f(x)\) sobre el\(x\) eje -eje y el\(y\) -eje
b. reflejando\(f(x)\) alrededor del\(x\) eje -eje, desplazando a la izquierda 2 unidades, y hacia abajo 3 unidades
34. Comenzando con la gráfica de\(f(x)= 4^{x}\) escribir la ecuación de la gráfica que resulta de
a. reflexionando\(f(x)\) sobre el\(x\) eje
b. reflejando\(f(x)\) alrededor del\(y\) eje -eje, desplazando hacia la derecha 4 unidades, y hacia arriba 2 unidades
Escribe una ecuación para cada función graficada a continuación.
35. 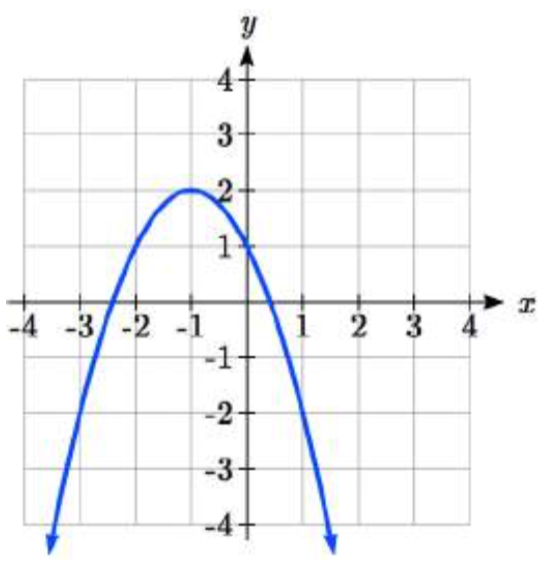 36.
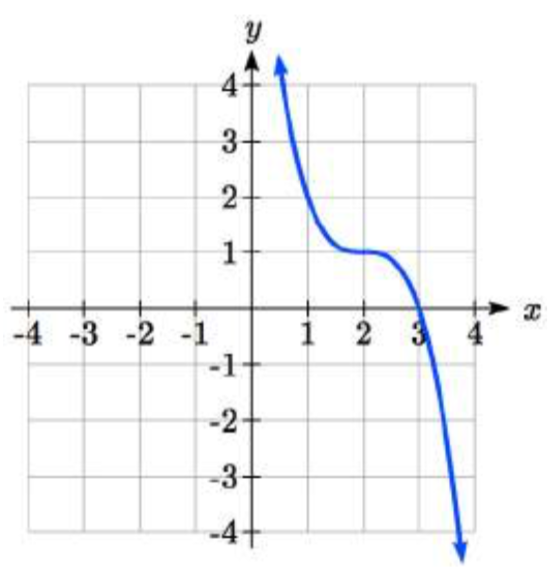
36. 
37. 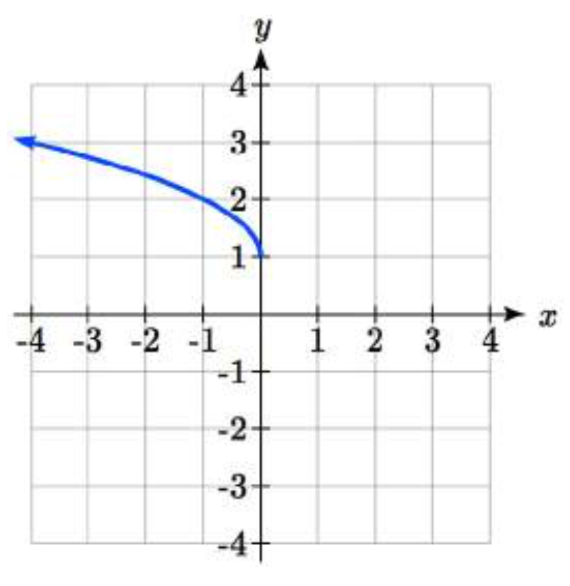 38.
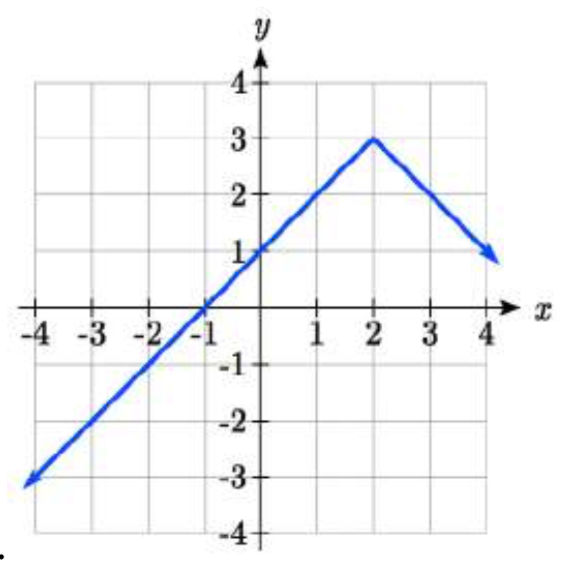
38. 
39. Para cada ecuación a continuación, determine si la función es impar, par o ninguno.
a.\(f(x)=3 x^{4}\)
b.\(g(x)=\sqrt{x}\)
c.\(h(x)=\dfrac{1}{x} +3 x\)
40. Para cada ecuación a continuación, determine si la función es impar, par o ninguno.
a.\(f(x)=(x-2)^{2}\)
b.\(g(x)=2 x^{4}\)
c.\(h(x)=2 x-x^{3}\)
Describir cómo cada función es una transformación de la función original\(f(x)\).
41. \(-f(x)\)
42. \(f(-x)\)
43. \(4f(x)\)
44. \(6f(x)\)
45. \(f(5x)\)
46. \(f(2x)\)
47. \(f(\dfrac{1}{3} x)\)
48. \(f(\dfrac{1}{5} x)\)
49. \(3f(-x)\)
50. \(-f(3x)\)
Escribe una fórmula para la función que resulta cuando la función del kit de herramientas dada se transforma como se describe.
51. \(f(x)=|x|\)reflejado sobre el eje y y comprimido horizontalmente por un factor de\(\dfrac{1}{4}\).
52. \(f(x)=\sqrt{x}\)reflejada sobre el eje x y estirada horizontalmente por un factor de 2.
53. \(f(x)=\dfrac{1}{x^{2} }\)comprimida verticalmente por un factor de\(\dfrac{1}{3}\), luego se desplazó hacia la izquierda 2 unidades y hacia abajo 3 unidades.
54. \(f(x)=\dfrac{1}{x}\)estirada verticalmente por un factor de 8, luego se desplazó hacia la derecha 4 unidades y hasta 2 unidades.
55. \(f(x)=x^{2}\)comprimido horizontalmente por un factor de\(\dfrac{1}{2}\), luego desplazado hacia la derecha 5 unidades y hasta 1 unidad.
56. \(f(x)=x^{2}\)se estiró horizontalmente por un factor de 3, luego se desplazó hacia la izquierda 4 unidades y hacia abajo 3 unidades.
Describir cómo cada fórmula es una transformación de una función de kit de herramientas. Después bosquejar una gráfica de la transformación.
57. \(f\left(x\right)=4(x+1)^{2} -5\)
58. \(g(x)=5(x+3)^{2} -2\)
59. \(h(x)=-2|x-4|+3\)
60. \(k(x)=-3\sqrt{x} -1\)
61. \(m(x)=\dfrac{1}{2} x^{3}\)
62. \(n(x)=\dfrac{1}{3} |x-2|\)
63. \(p(x)=(\dfrac{1}{3} x)^{2} -3\)
64. \(q(x)=(\dfrac{1}{4} x)^{3} +1\)
65. \(a(x)=\sqrt{-x+4}\)
66. \(b(x)=\sqrt[{3}]{-x-6}\)
Determinar el (los) intervalo (s) en el que la función está aumentando y disminuyendo.
67. \(f(x)=4(x+1)^{2} -5\)
68. \(g(x)=5(x+3)^{2} -2\)
69. \(a(x)=\sqrt{-x+4}\)
70. \(k(x)=-3\sqrt{x} -1\)
Determinar los intervalos en los que la función es cóncava hacia arriba y cóncava hacia abajo.
71. \(m(x)=-2(x+3)^{3} +1\)
72. \(b(x)=\sqrt[{3}]{-x-6}\)
73. \(p(x)=(\dfrac{1}{3} x)^{2} -3\)
74. \(k(x)=-3\sqrt{x} -1\)
La función\(f(x)\) se grafica aquí. Escriba una ecuación para cada gráfica a continuación como una transformación de\(f(x)\).
75. 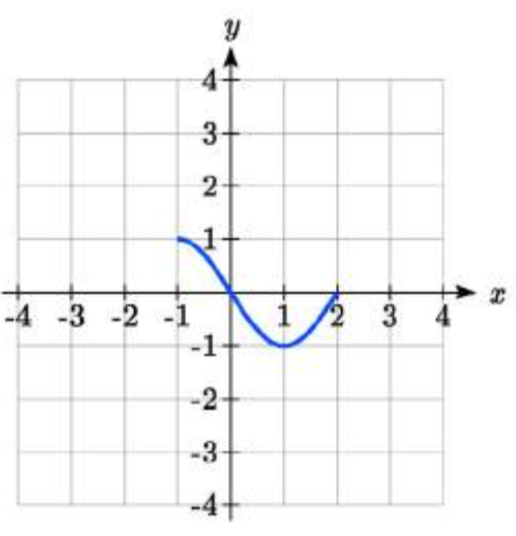 76.
76. 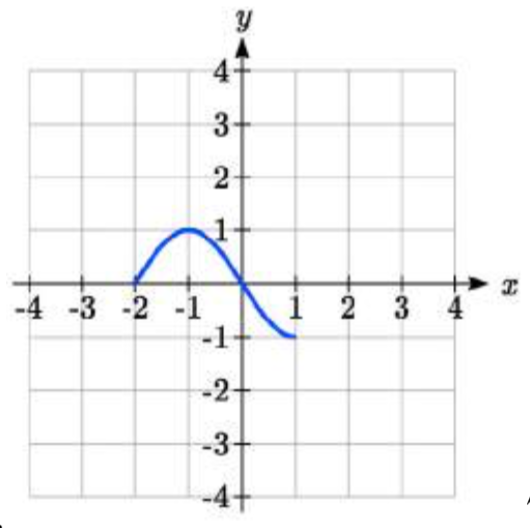 77.
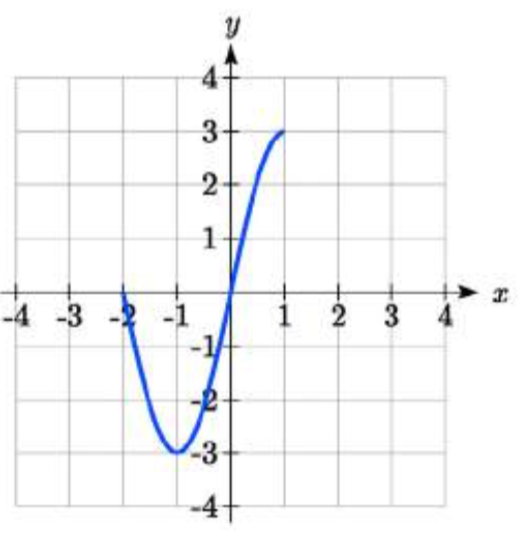
77. 
78. 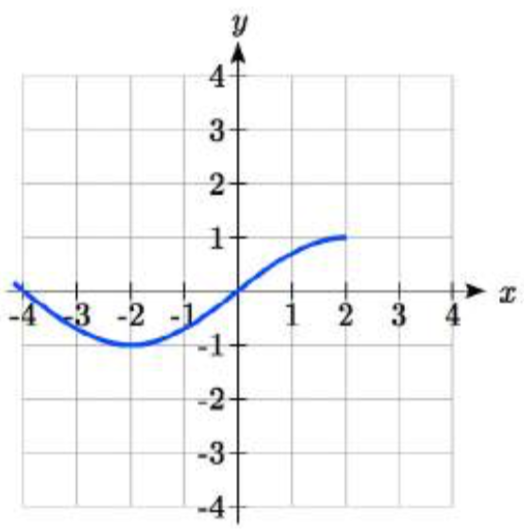 79.
79. 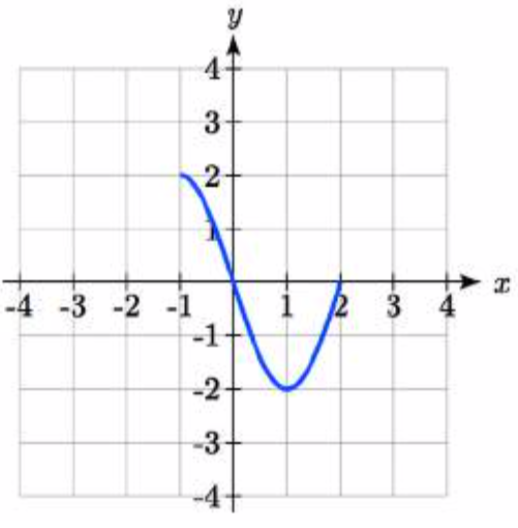 80.
80. 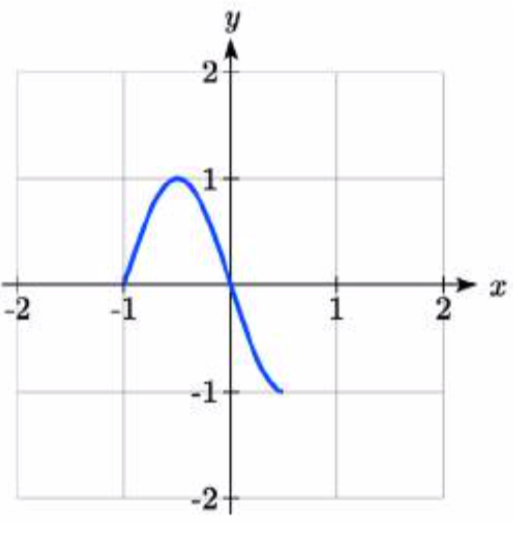
81. 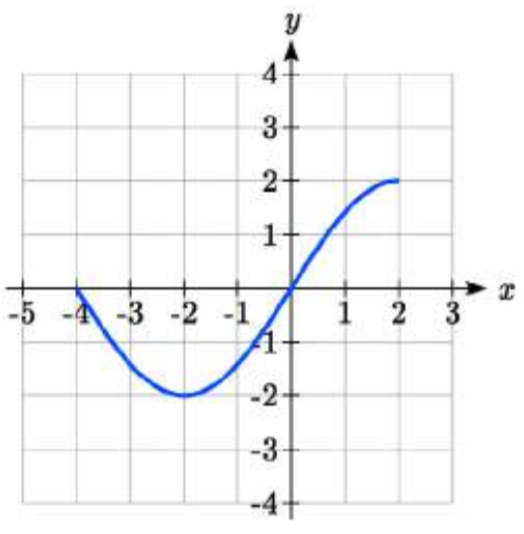 82.
82. 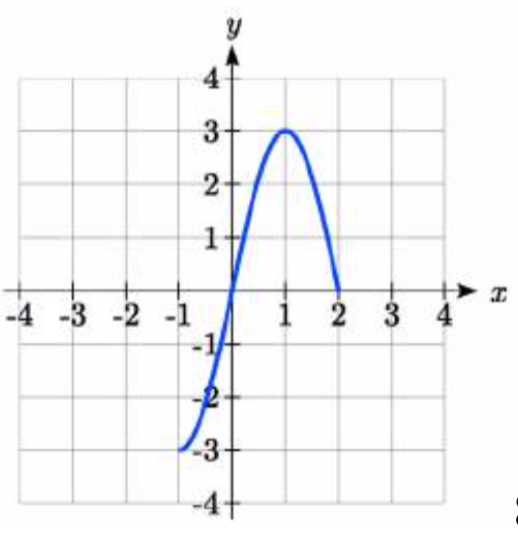 83.
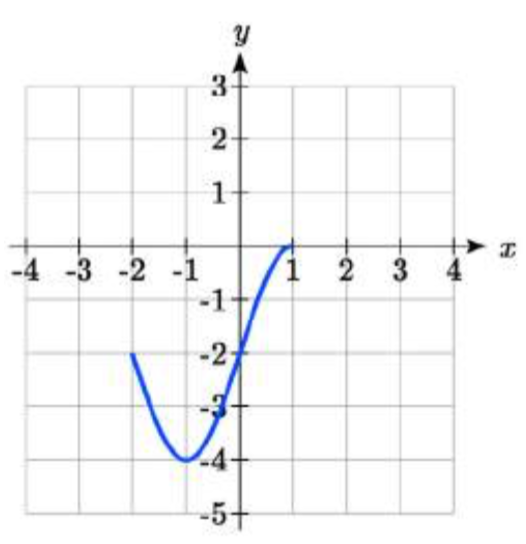
83. 
84. 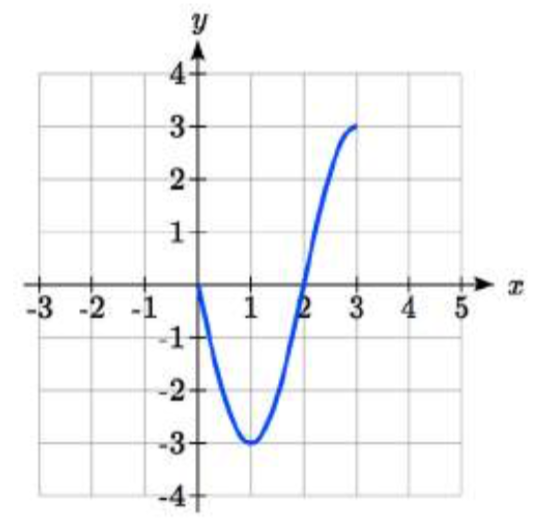 85.
85. 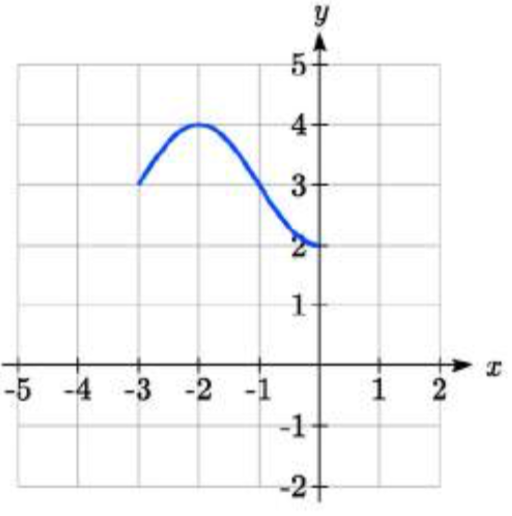 86.
86. 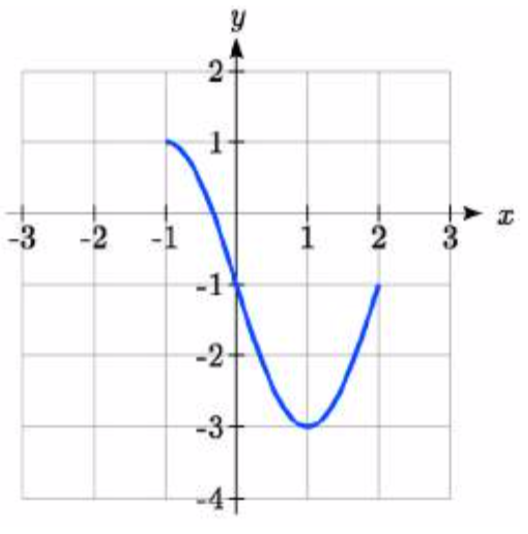
Escriba una ecuación para cada función del kit de herramientas transformada que se muestra a continuación.
87. 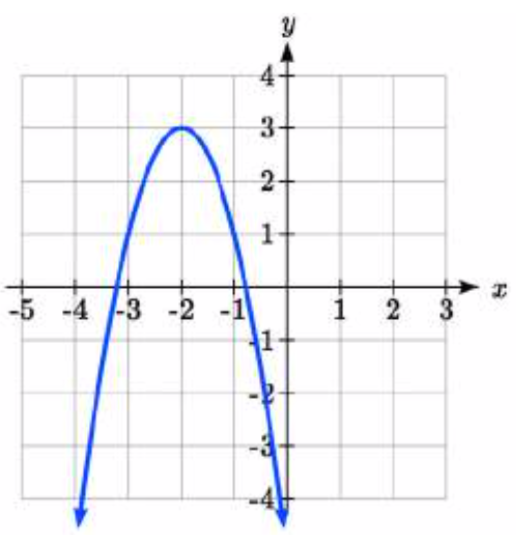 88.
88. 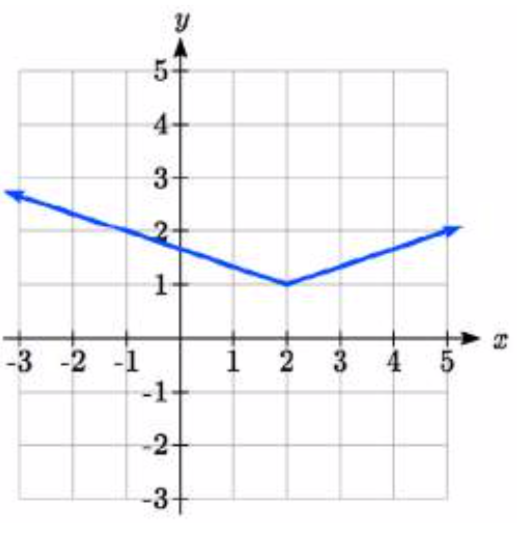 89.
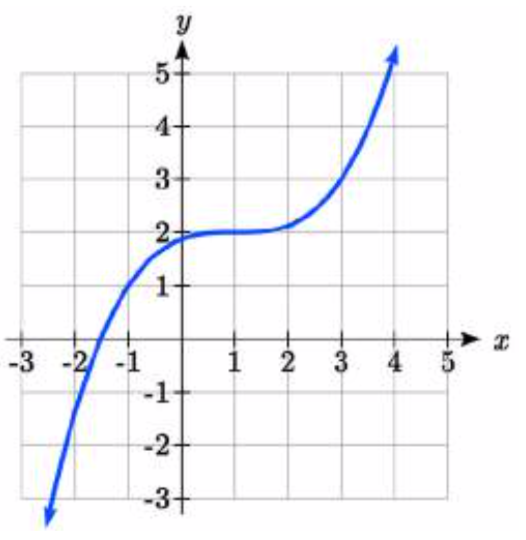
89. 
90. 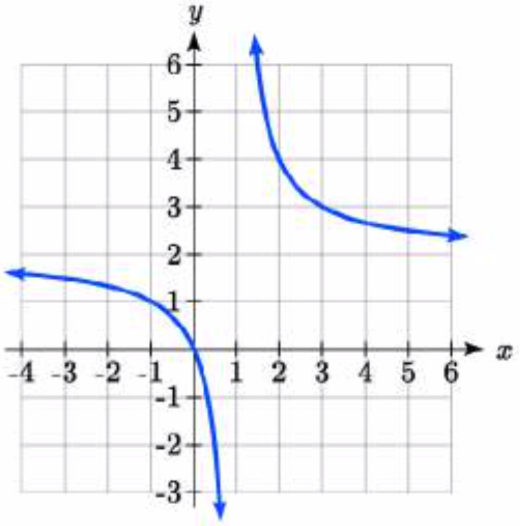 91.
91. 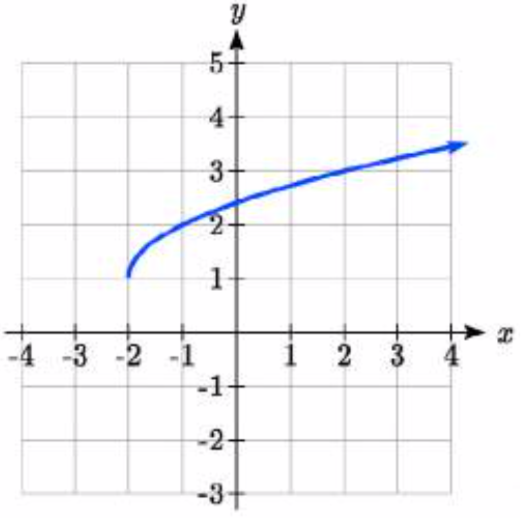 92.
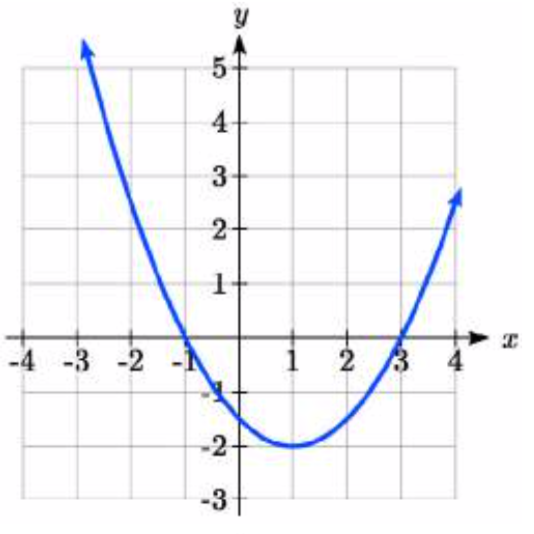
92. 
93. 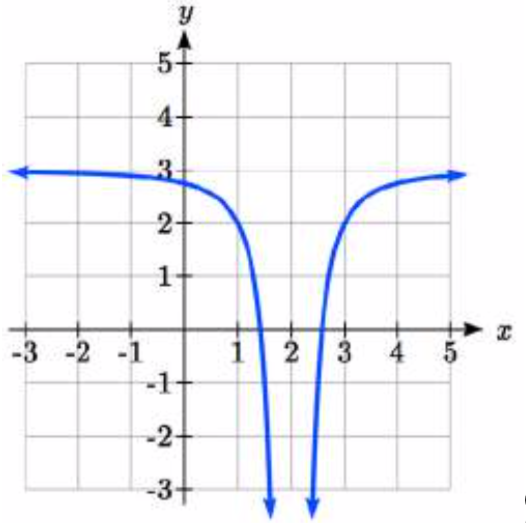 94.
94.  95.
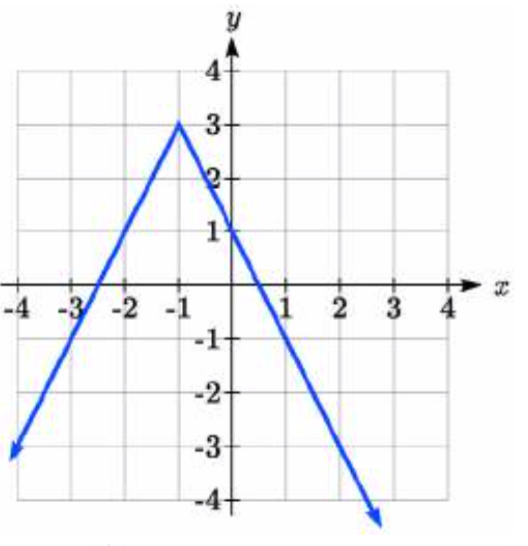
95. 
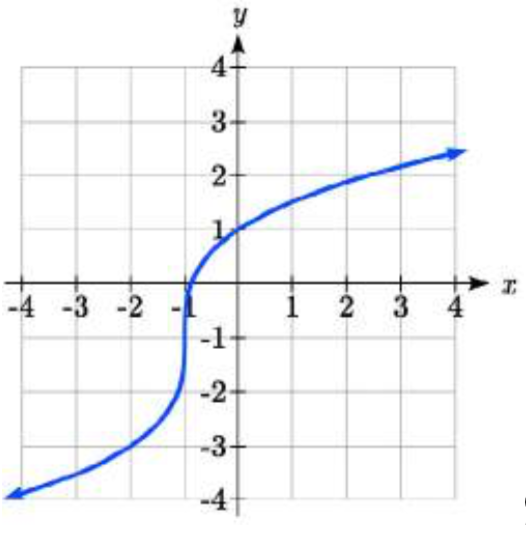
96. 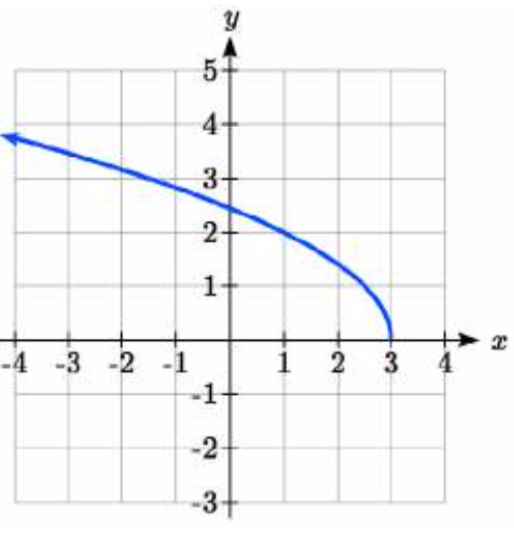 97.
97. 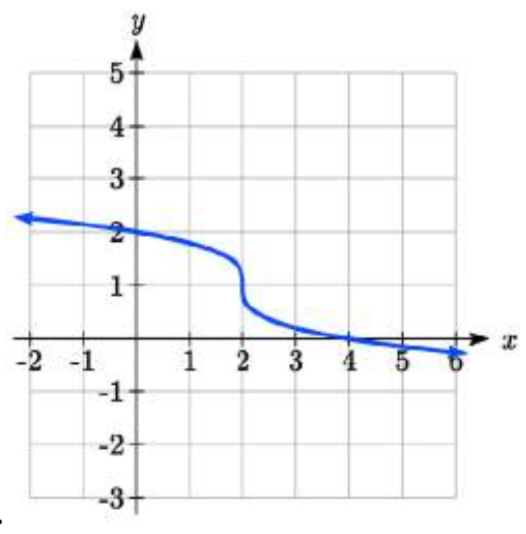 98.
98. 
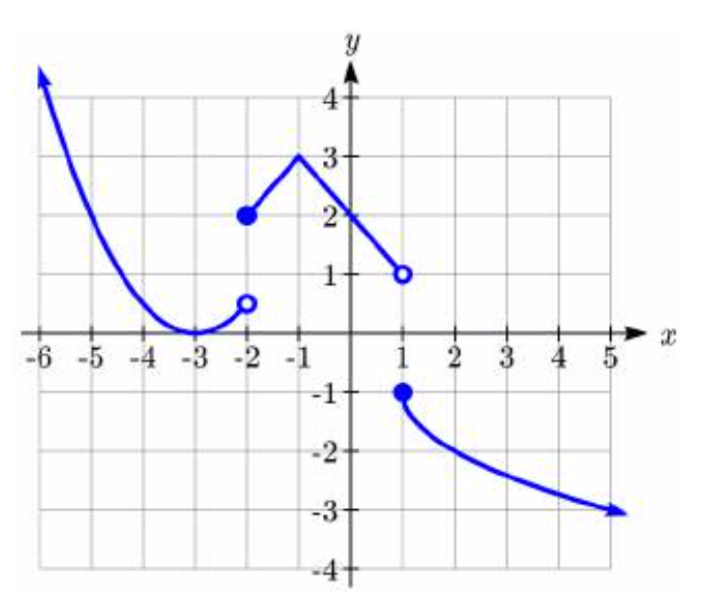
Escribe una fórmula para la función por partes que se muestra a continuación.
99. 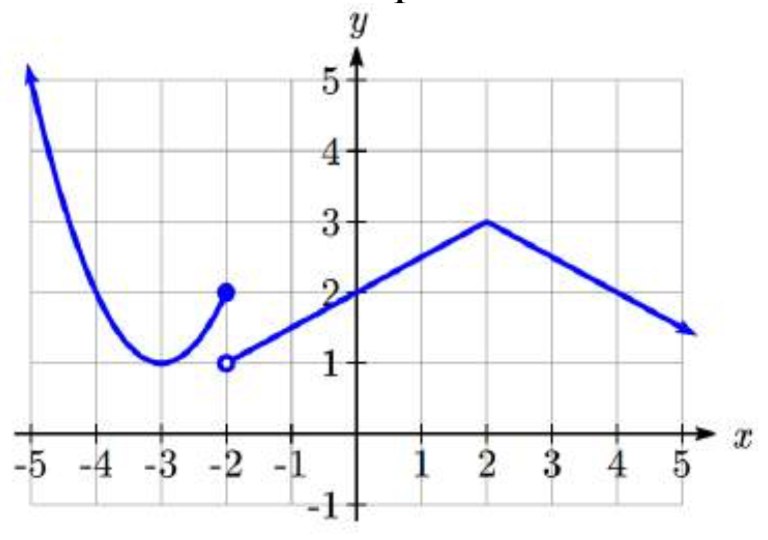 100.
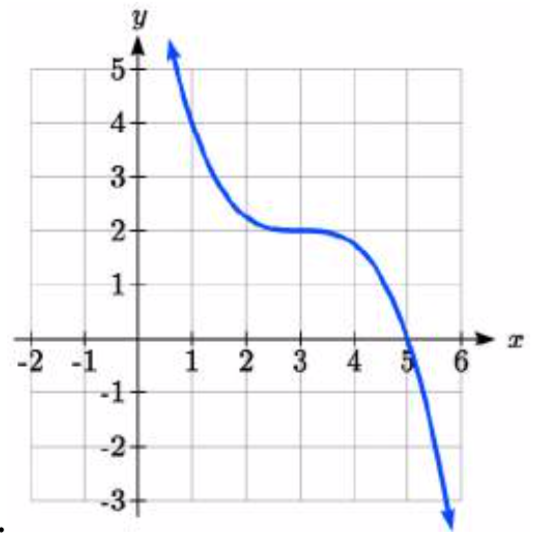
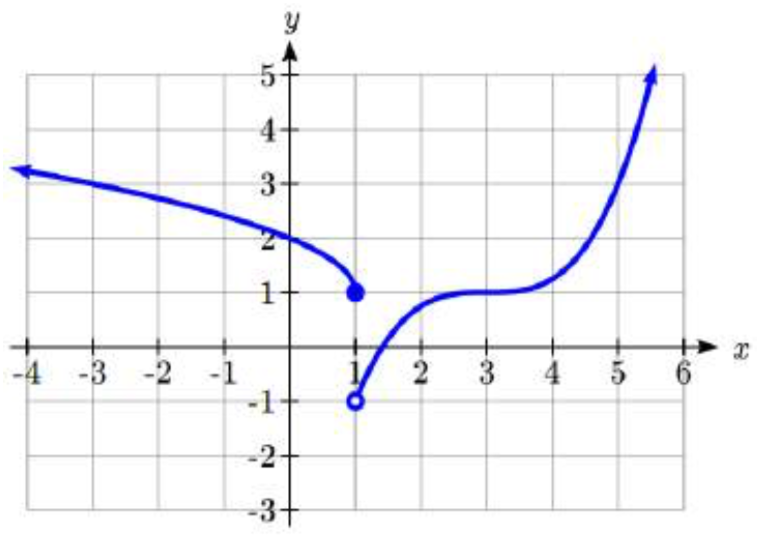
100. 
101. 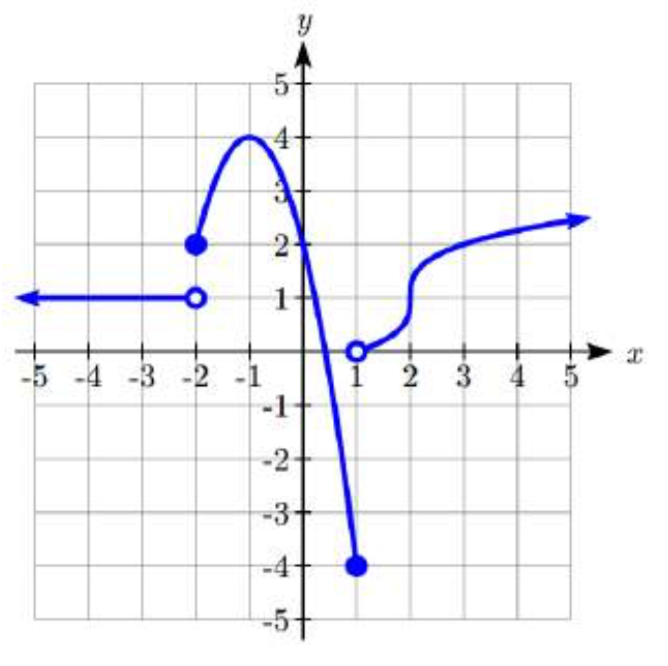 102.
102. 
103. Supongamos que tiene una función\(y = f(x)\) tal que el dominio de\(f(x)\) is\(1 \le x \le 6\) y el rango de\(f(x)\) es (-3\ le y\ le 5\). [UW]
a. ¿Cuál es el dominio\(\; f(2(x-3))\;\)?
b. ¿Cuál es el rango de\(f(2(x-3))\)?
c. ¿Cuál es el dominio\(2f(x)-3\)?
d. ¿Cuál es el rango de\(2f(x)-3\)?
e. ¿Se pueden encontrar constantes\(B\) y\(C\) para que el dominio de\(f(B(x-C))\) sea\(8 \le x \le 9\)?
f. se pueden encontrar constantes\(A\) y\(D\) para que el rango de\(Af(x) + D\) sea 0\(0 \le y \le 1\)?
- Contestar
-
1. Desplazamiento horizontal a la derecha 49 unidades
3. Desplazamiento horizontal a la izquierda 3 unidades
5. Desplazamiento vertical hacia arriba 5 unidades
7. Desplazamiento vertical hacia abajo 2 unidades
9. Desplazamiento horizontal derecho 2 unidades, Desplazamiento vertical hacia arriba 3 unidades
11. \(f(x + 2) + 1 = \sqrt{x + 2} + 1\)
13. \(f(x - 3) - 4 = \dfrac{1}{x - 3} - 4\)
15. \(g(x) = f(x - 1)\),\(h(x) = f(x) + 1\)
17.
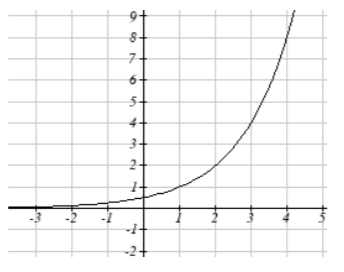
 19.
19. 
21.
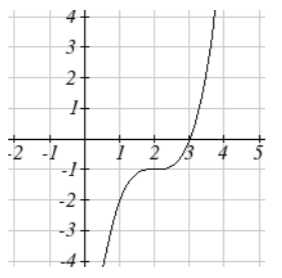
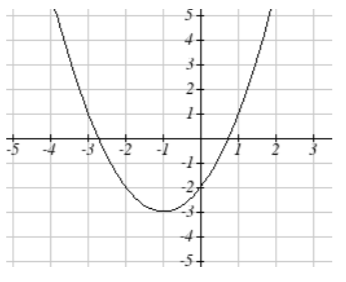 23.
23. 
25. \(y = |x - 3| - 2\)
27. \(y = \sqrt{x + 3} - 1\)
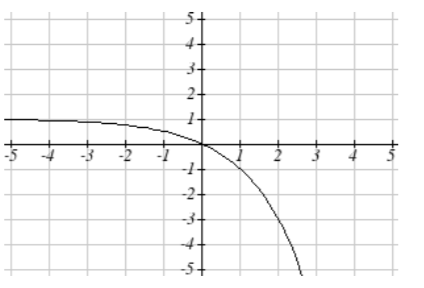
29. \(y = -\sqrt{x}\)
31.
33. a.\(-f(-x) = -6^{-x}\)
b.\(-f(x + 2) - 3 = -6^{x + 2} - 3\)35. \(y = -(x + 1)^2 + 2\)
37. \(y = \sqrt{-x} + 1\)
39. a. Par
b. Ninguno
c. Impares41. Reflexionar\(f(x)\) sobre el\(x\) eje
43. Estirar verticalmente\(y\) los valores en 4
45. Comprimir horizontalmente\(x\) los valores en 1/5
47. Estirar\(x\) valores horizontalmente en 3
49. Reflexionar\(f(x)\) sobre el\(y\) eje -y estirar verticalmente\(y\) los valores en 3
51. \(f(-4x) = |-4x|\)
53. \(\dfrac{1}{3} f(x + 2) - 3 = \dfrac{1}{3(x + 2)^2} - 3\)
55. \(f(2(x - 5)) + 1 = (2 (x - 5))^2 + 1\)
57. Desplazamiento horizontal a la izquierda 1 unidad,\(y\) valores de estiramiento vertical por 4, desplazamiento vertical hacia abajo 5 unidades
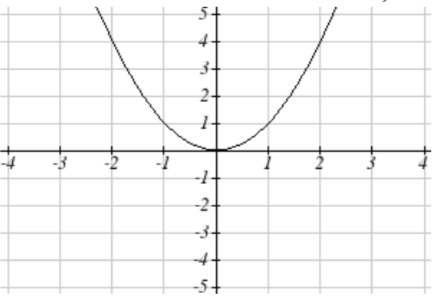 se convierte
se convierte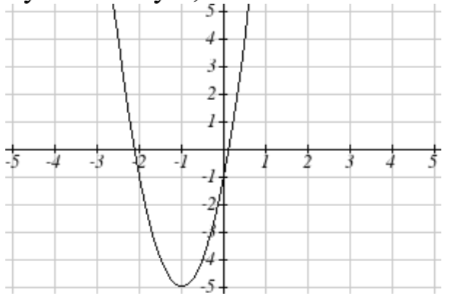
59. Desplazamiento horizontal a la derecha 4 unidades,\(y\) valores de estiramiento vertical en 2, reflejar sobre el\(x\) eje, desplazar verticalmente hacia arriba 3 unidades.
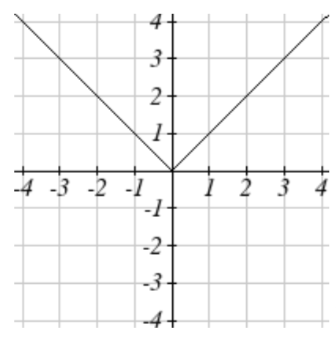 se convierte
se convierte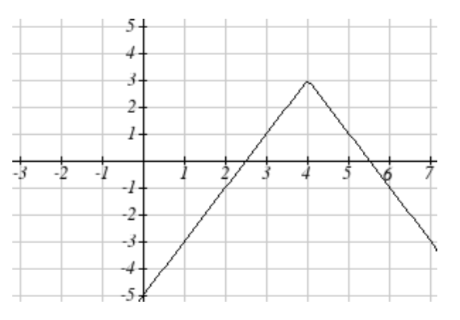
61. Comprimir verticalmente\(y\) valores en 1/2
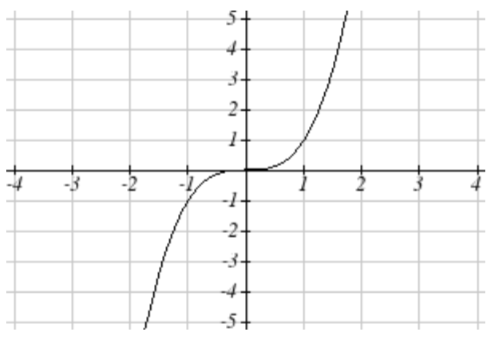 se convierte
se convierte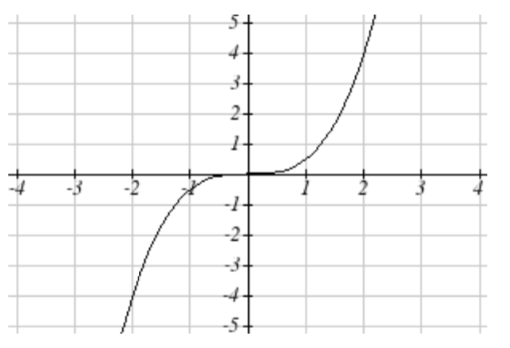
63. Estirar horizontalmente\(x\) los valores por 3, desplazamiento vertical hacia abajo 3 unidades
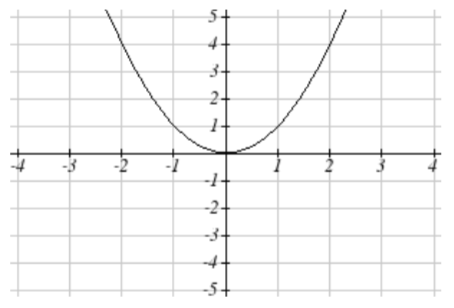 se convierte
se convierte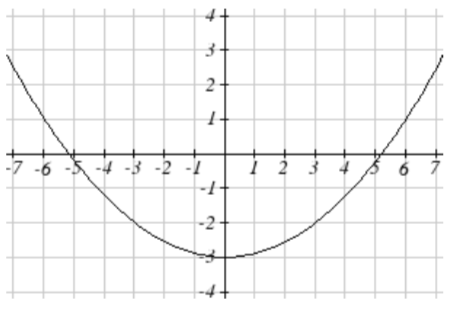
65. Reflejado sobre el\(y\) eje, desplazamiento horizontal a la derecha 4 unidades\(a(x) = \sqrt{-(x - 4)}\)
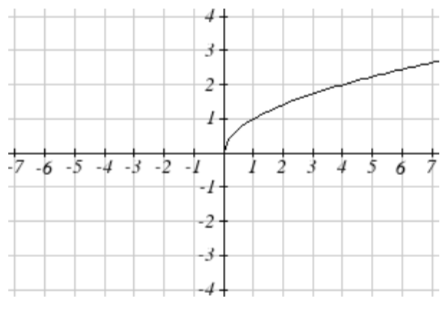 se convierte
se convierte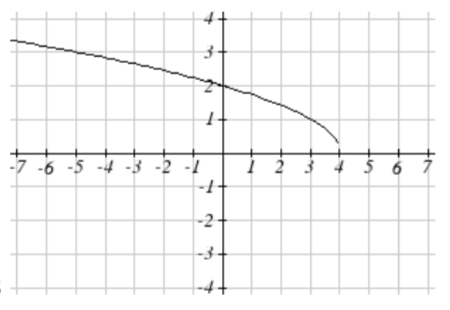
67. Esta función está aumentando\((-1, \infty)\) y disminuyendo en\((-\infty, -1)\)
69. Esta función está disminuyendo en\((-\infty, 4)\)
71. Esta función es cóncava hacia abajo\((-3, \infty)\) y cóncava hacia arriba\((-\infty, -3)\)
73. Esta función es cóncava en todas partes
75. \(f(-x)\)
77. \(3f(x)\)
79. 2\(f(-x)\)
81. \(2f(\dfrac{1}{2}x)\)
83. \(2f(x) - 2\)
85. \(-f(x + 1) + 3\)
87. \(y = -2(x + 2)^2 + 3\)
89. \(y = (\dfrac{1}{2} (x - 1))^3 + 2\)
91. \(y = \sqrt{2(x + 2)} + 1\)
93. \(y = \dfrac{-1}{(x - 2)^2} + 3\)
95. \(y = -2|x + 1| + 3\)
97. \(y = \sqrt[3]{-\dfrac{1}{2}(x - 2)} + 1\)
99. \(f(x) = \begin{cases} (x+3)^2 + 1 & if & x \le -2 \\ \dfrac{1}{2}|x - 2| + 3 & if & x > -2 \end{cases}\)
101. \(f(x) = \begin{cases} 1 & if & x < -2 \\ -2(x + 1)^2 + 4 & if & -2 \le x \le 1 \\ \sqrt[3]{x - 2} + 1 & if & x > 1 \end{cases}\)
103a. Dominio:\(3.5 \le x \le 6\)
d. Rango:\(-9 \le y \le 7\)

